Gen Zhang(張根), Li-Zheng Lv(呂李政), Peng Gao(高鵬), and Zhan-Ying Yang(楊戰(zhàn)營(yíng)),4,?

1School of Physics,Northwest University,Xi’an 710127,China

2Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China

3Graduate School,China Academy of Engineering Physics,Beijing 100193,China

4Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China

Keywords: dipolar Bose–Einstein condensates,soliton,soliton collision

1.Introduction

The interaction between solitons has always been a hot topic in research due to its rich dynamical behavior.[1–8]The phase shift that occurs after elastic collision between solitons reveals the nature of particle-like.[4,5]The theoretical analysis of the interaction between bright solitons in potential wells has led to the observation of interference patterns.[8]In recent years, the realization of dipolar Bose–Einstein condensates (BECs) has provided a new direction for studying soliton interactions.[9–15]The atoms that make up dipolar BECs have large magnetic dipole moment, which gives rise to the occurrence of dipole–dipole interactions.Dipole–dipole interaction is an anisotropic long-range interaction, which is fundamentally different from the isotropic short-range contact interaction.[16–22]The long-range feature of dipole–dipole interactions allows for the stabilization of multidimensional solitons and new local waves (such as soliton molecules and dark solitons with ripples[23–26]), while the anisotropic feature facilitates the formation of anisotropic solitons (such as anisotropic bright and vortex solitons[27,28]).Therefore, exploring the nonlinear excitation dynamics under dipole–dipole interactions is an important topic in ultracold atom systems.

The extensive research has been conducted on the interaction between solitons in finite-component systems.In single-component BECs systems, the formation and propagation of bright solitons in7Li atoms,[29,30]as well as the collision dynamics between these solitons,[2]have been studied extensively.Compared with single-component BECs,multi-component BECs exhibit richer dynamics as they not only have intraspecies interactions but also have interspecies interactions.[19,31–33]For example, vector solitons such as bright–bright solitons[34–36]and dark–dark solitons[37,38]have been theoretically predicted in multi-component BECs.

As we know, there has been a lack of research on soliton interactions in multi-component dipolar BECs systems.Therefore,the study of soliton collision dynamics in this system is worthy of more attention.There are some important unresolved issues.(i)In single-component dipolar BECs,soliton interactions lead to breathing phenomena.Can multicomponent dipolar BECs bring more various dynamic phenomena? (ii) How to control these nonlinear excitations and characterize their regularity? Based on these questions, our research is carried out.

In this paper,we investigate the interaction between solitons in a binary dipolar BECs system.The numerical results indicate that the collision of two bright solitons can induce special breathing structures,such as snakelike special breathing structure (SS), mixed breathing structure (MS), and divided breathing structure (DS).We have demonstrated that the existence of these three special breathing structures depends on traditional breathing solitons(TS).And their breathing properties are closely related to the atomic numberNiand interspecies scattering lengtha12.Meanwhile, we find that the lifetime of the MS structure can also be manipulated by atomic numberNiand interspecies scattering lengtha12.In addition,the collision between these special breathing structures can also bring some interesting dynamics.After the collision of SS and DS structures of the same type, they can maintain their own stability.When two MS structures of the same type collide, they exhibit different breathing dynamics at different velocities.Our research results demonstrate that collisions between bright solitons in a binary dipolar BECs system lead to richer breathing dynamics,providing a reference for future studies of solitons and their interactions in multi-component dipolar BECs systems.

2.Model of the binary dipolar BECs

The dynamics of binary dipole BECs can be described by the coupled Gross–Pitaevskii(GP)model[22,39,40]

we consider a bright soliton in a binary dipole BECs whose mass,atomic number,and scattering length for the two speciesi= 1,2, given bymi,Niandai, respectively.Ψi(r,t) is the mean-field wave function of condensates.The third and fourth terms on the right side of the equation represent intraspecies and interspecies contact interactions, and the fifth and sixth terms represent intraspecies and interspecies dipole interactions.Herea12represents the interspecies scattering length,μ0is the permeability of the free space, andmR=m1m2/(m1+m2)is the reduced mass.The external potentialVi(r) provides a trap where the cloud is confined, and it can be assumed as a harmonic form,Vi(r)=miωi2ρ2,whereωiis the angular frequencies of the traps acting on the two species in the transverseρdirection(here,ω1=ω2).Meanwhile,axial trap is ignored.The nonlocal dipolar potential is

The experimental values of the scattering lengths we considered are all known, except for the intraspecies scattering length of168Er atoms.Preliminary cross-dimensional thermalization measurements indicate that the scattering length is between 150a0and 200a0.[10]The scattering length can be experimentally controlled independently by magnetic[42]and optical[43]Feshbach resonance techniques.The dipole interaction strengthgdcan be changed by adjustingα.In contrast to single-component dipolar BECs,binary dipolar BECs not only have intraspecies interactions but also have dipole–dipole interactions.Interspecies scattering lengtha12plays an essential role in the study of binary bright solitons,leading to richer dynamic phenomena.[44]Therefore, we aim to explore the influence of interspecies scattering lengtha12on soliton properties in binary dipolar BECs.For164Dy atoms, we takea1=-120a0, and for168Er atoms, we takea2=-60a0, in addition setα=1.

3.Breathing dynamics of solitons induced by collision

It is an effective method to investigate the dynamic characteristics of solitons by the collision between solitons.We give the initial conditions for two solitons with opposite velocities

wherez0>0 andv ≥0 are the initial offset and velocity of solitons,respectively.

We consider the case of the attractive dipole interaction (intraspecies and interspecies) and attractive contact interaction (intraspecies and interspecies).We can obtain stable bright solitons and BECs in a reasonable research range.In the numerical simulation, we adopt the split-step Fourier method to implement the amplitude evolution|ψ(z,t)|.Here, Figs.1(a1)–1(c1) represent the first component and Figs.1(a2)–1(c2)represent the second component.The initial parameters area12=-60a0,N1=1,N2=2,z0=5,v=0.8 and the plot of amplitude evolution of the first component is illustrated in Fig.1(a1).The result reveals that an SS structure is observed on the left side of thez-axis after the collision,and a TS structure with a stable breathing frequency is formed on the right side.Meanwhile, the plot of amplitude evolution of the second component is depicted in Fig.1(a2),the TS structure is formed on the left side of thez-axis after collision,and the SS structure is observed on the right side.Here, we distinguish the difference between the TS structure and the SS structure based on the variation in their peak amplitude.The TS structure exhibits peak amplitude oscillations in the center,whereas, for the SS structure, the peak amplitude oscillates around the center in a snake pattern.They all have a stable breathing frequency.Then,we consider the initial parameters ofa12=-60a0,N1= 3,N2= 1,z0= 5,v= 0.6, and the amplitude evolution|ψ1(z,t)|of the first component is shown in Fig.1(b1).After the collision, we observe the SS structure on the left side of thez-axis, and the TS structure on the right side.However,due to the first component having a larger number of atoms,it can maintain stability more effectively after collision,resulting in a relatively small and inconspicuous SS structure.The amplitude evolution|ψ2(z,t)|of the second component is shown in Fig.1(b2),we observe the TS structure on the left side of thez-axis after collision, and a unique DS structure appears on the right side.When the initial parameters area12=-100a0,N1=0.5,N2=1,z0=5,v=0.6,the amplitude evolution|ψ1(z,t)|of the first component is shown in Fig.1(c1).We find that the DS structure can converge to form an SS structure over time, appearing on the left side of thez-axis after collision.And the TS structure forms on the right side.This mixed breathing structure is called the MS structure.There is a TS structure on the left side ofz-axis after collision and an SS structure on the right side of the second component,as shown in Fig.1(c2).

Up to now, we have obtained three special breathing structures by simulating the collision of two bright solitons in binary dipole BECs, in which SS structure, MS structure and DS structure all exist rely on the TS structure.In this paper,we mainly excite three special breathing structures,which bring some novel breathing dynamics.Next, we will explore the conditions under which these breathing structures are excited.

To investigate the special breathing structures,we present phase diagrams in a space defined by atomic numberNiand interspecies scattering lengtha12.Specifically,Figs.2(a)and 2(c) are associated with the left side of thez-axis after collision,while Figs.2(b)and 2(d)correspond to the right side of thez-axis.When the number of164Dy atomN1=1,Fig.2(a)shows the distribution of breathing structures for differentN2anda12.Here,the red region corresponds to the excitation of SS and TS structures(first and second components),while the blue region corresponds to the excitation of MS and TS structures(first and second components).Furthermore,in Fig.2(b),we give the excitation conditions of TS and DS structures(first and second components)in the green area and ones of TS and SS structures(first and second components)in the red area.It is evident from Figs.2(a)and 2(b)that the quasi-transition between different types of special structures is dependent on the atomic numberNiand the interspecies scattering lengtha12.In the quasi-transition process, the atomic numberNiplays a more important role.The result indicates that when the atomic number of the second component is larger than that of the first component, a stable SS structure in the first component can gradually separate into MS structures.And the divided DS structures in the second component can gradually turn into stable SS structures.

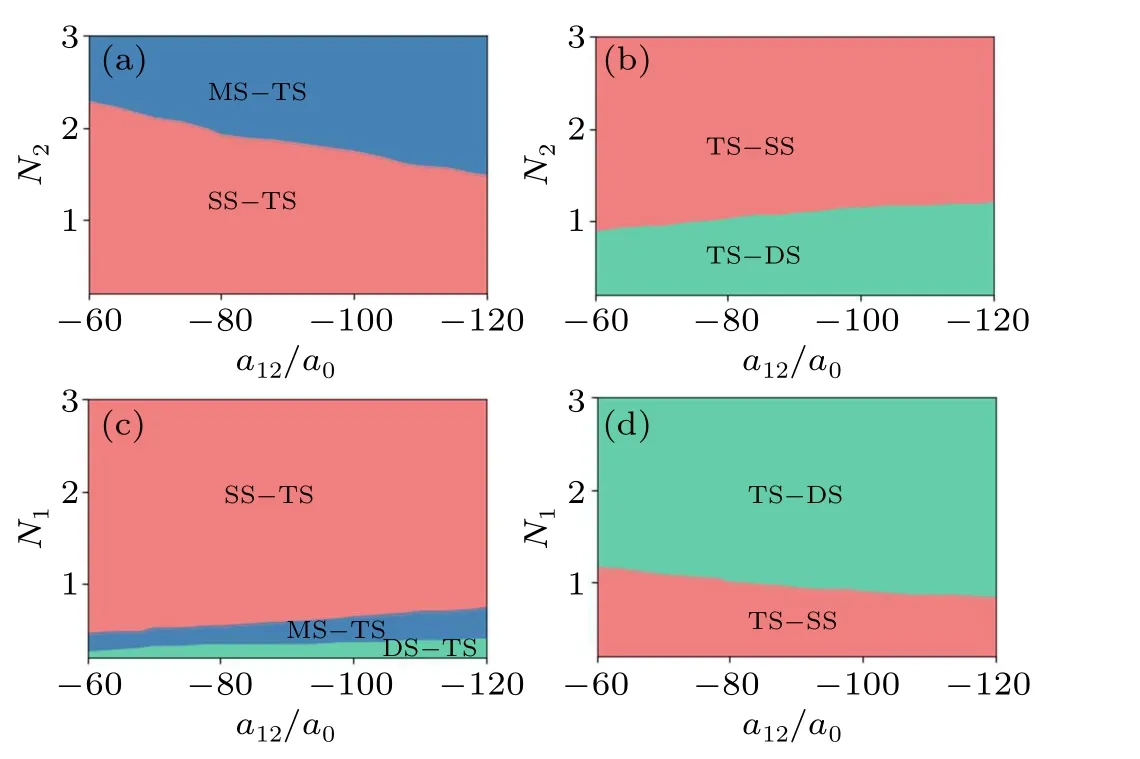
Fig.2.The phase diagrams depict the special breathing structure observed after a collision between binary 164Dy–168Er solitons.When N1=1,(a)and(b)depict the special breathing structures that are respectively excited on the left and right sides following the collision along the z-axis.When N2 =1,(c)and(d)depict the special breathing structures that are respectively excited on the left and right sides following the collision along the z-axis.The front of the bar indicates the first component,and the back of the bar indicates the second component.The parameters used in the numerical simulation are a1=-120a0,a2=-60a0,v=0.6,z0=5.

Fig.3.Effect of atomic number Ni and interspecies scattering length a12 on the maximum value of the breathing amplitude A and frequency? of three breathing structures: SS,DS,MS(from left to right).The initial condition for panel(a1)N1 =1,a12 =-60a0,panel(b1)N2 =1,a12=-60a0,panel(a2)N1=1,N2=2,panel(b2)N1=3,N2=1,where the solid red line indicates the breathing frequency ?,and the solid black line indicates the maximum value of the breathing amplitude A.In panel(c1)N1=1,a12=-100a0 and in panel(c2)N1=0.4,N2=1,where the solid red and black lines represent breathing frequency ?1 and the maximum value of the breathing amplitude A1 before mixing,respectively,and the red and black dashed lines represent the breathing frequency ?2 and the maximum value of the breathing amplitude A2 after mixing,respectively.The other parameters are z0=5,v=0.6.

When the number of168Er atomN2=1,in Fig.2(c),the green area excites DS and TS structures(first and second components),the blue area excites MS and TS structures(first and second components),and the red area excites SS and TS structures(first and second components).As the atomic numberN1increases,the quasi-transition from DS structure to MS structure to SS structure can be achieved in the first component.In Fig.2(d),the red region excites the TS and SS structures(the first and second components)and the green region excites the TS and DS structures (the first and second components).As the atomic numberN1increases,the quasi-transition from the SS structure to the DS structure can be achieved in the second component.

In the case wherea12=-60a0,N1= 1, our findings indicate that the maximum breathing amplitudeAand frequency?of the SS structure increase asN2increases, as shown in Fig.3(a1).Additionally, whenN1= 1,N2= 2,the maximum breathing amplitudeAand frequency?of the SS structure increase with increasing interspecies scattering lengtha12, as demonstrated in Fig.3(a2).Therefore, we manipulate the maximum breathing amplitudeAand frequency?of the SS structure by atomic numberNiand interspecies scattering lengtha12.As mentioned earlier, the DS structure comprises two columns of breathing solitons that are nearly identical.So,the maximum breathing amplitudeAand breathing frequency?of DS structure are described by the average of the two columns of breathing solitons.In the scenario wherea12=-60a0,N2=1,the findings indicate that the maximum breathing amplitudeAand breathing frequency?of the DS structure increase with increasingN1, as illustrated in Fig.3(b1).Conversely, in the case ofN1=3,N2=1, the maximum breathing amplitudeAof the DS structure gradually decreases with increasing interspecies scattering lengtha12, while the breathing frequency?gradually increases, as demonstrated in Fig.3(b2).Furthermore,we have a new discovery for the MS structure,which is comparable to the quasitransition stage of divided DS structure turning into an SS structure.Therefore,the MS structure research is divided into two categories: pre-mixing and post-mixing.During numerical simulations, we designate the collision time point as the initial time, pre-mixing as the time period from 0 to 10, and post-mixing as the time period from 50 to 60.A1,A2,?1,and?2represent the maximum breathing amplitude and frequency before and after mixing, respectively.Fora12=-100a0,N1= 1, the results indicate that asN2increases, the maximum breathing amplitudes (A1andA2) of the MS structure before and after mixing gradually decrease, while the breathing frequencies(?1and?2)before and after mixing progressively increase, as illustrated in Fig.3(c1).In the case whereN1=0.4,N2=1,the findings indicate that with increasing interspecies scattering lengtha12, the maximum breathing amplitudeA1of the MS structure before mixing gradually decreases,while the maximum breathing amplitudeA2after mixing gradually increases.Moreover, the breathing frequency(?1and?2)before and after mixing progressively increases,as illustrated in Fig.3(c2).

When studying the breathing character of the MS structure, we find that the lifetimeτof the MS structure is influenced by atomic numberNiand interspecies scattering lengtha12.

The outcomes depicted in Fig.4(b) demonstrate that the centroid coordinates gradually approach the 0-axis over time.To determine the lifetimeτ, we refer to the amplitude evolution diagram of the MS structure displayed in Fig.4(a)and integrate the centroid coordinates to obtain a reasonable threshold.During the numerical simulations, we set the time precision to ?t=0.002 and the time interval tot0=3.Based on statistical analysis,we confirm that whenP<1.6,a mixed state is reached.In Fig.4(c), we observe that the lifetimeτdecreases as the atomic numberN1increases whenN2=1,a12=-100a0.In Fig.4(d), we demonstrate that an increase in the interspecies scattering lengtha12results in an increase in the lifetimeτ,whenN1=0.5,N2=1.

Fig.4.When N1=0.5,a12=-100a0,N2=1,(a)amplitude evolution plot of MS structure and (b) the centroid coordinate plot corresponding to the MS structure amplitude evolution plot.(c) The variation in lifetime with the atomic number N1 when a12 =-100a0, N2 =1.(d) The variation in lifetime with the interspecies scattering length a12 when N1=0.5,N2=1.

4.Interaction between three special breathing structures

We have successfully induced three unique breathing structures through the collision of bright solitons,resulting in rich breathing dynamics.Next,we want to explore the interactions among these distinctive breathing structures.In numerical simulations,we apply the super-Gaussian function to filter the dip profile and weaken the radiation waves outside the soliton to better illustrate the collision dynamics.Consequently,the initial condition is changed into

The above initial conditions include three special breathing structures,such as SS structures,DS structures and MS structures.They are both made up of medial peaks and lateral peaks.As shown in the Fig.5(a) for MS structure, the peak near the 0-axis is the medial peak,and the one far away from the 0-axis is the lateral peak,denoted as M and L respectively.The result reveals that the collision between two identical SS or DS structures does not change their respective breathing types.In other words, they remain as SS or DS structures after collision.However, when two identical MS structures collide,it significantly impacts their breathing properties.For instance, the collision can lead to changes in their lifetime.Based on the findings displayed in Fig.5(a),it is evident that two MS structures can sustain their individual type for an extended period after collision, indicating a longer lifetime.However,from Fig.5(b),it is observed that two MS structures collide and rapidly transform into SS structures, implying a shorter lifetime.The difference in velocity under the initial conditions is responsible for this result.Consequently,we utilize the collision timetcto describe the effect of velocity on its lifetimeτ.Next,we explore the relationship between the lifetimeτof MS structures and the collision timetc.During the numerical evolution,the time period of both medial and lateral peaks is denoted asTDS=1.33.The research results,as shown in Fig.5(c), indicate that collisions play a crucial role in the lifetime of MS structure, and its lifetime presents a periodic change withtc.Subsequent to the collision, the SS structure formation time period is approximatelyTSS= 1.4, whereas the MS structure formation time period is aboutTMS=1.3.From the figure,it is evident that the maximum lifetime of the MS structure post-collision consistently falls within the interval spanning from M to L.The collision between two different breathing structures can also alter the breathing types and breathing properties of the SS structure,MS structure,and DS structure.Collisions at different velocities can result in mutual transformations among these three special breathing structures,namely the SS structure,MS structure,and DS structure.

Fig.5.When N1=0.5,N2=1,a12=-100a0,z0=10,the amplitude evolution plots for the collision of two MS structures at time(a)tc=6,and(b)tc=7.(c)The variation of the lifetime τ of MS structures after collision with respect to the collision time tc.The black solid line represents the lifetime τ of the MS structure after collision,and the solid red line represents the lifetime τ of the MS structure without interaction.

5.Conclusion

We conduct numerical studies on the collision process of bright solitons in a binary dipolar BECs system.The breathing phenomenon of solitons after collision is caused by the attractive dipole–dipole interaction and contact interaction.After the collision,we obtain three special breathing structures,such as SS structure, MS structure, and DS structure.The characteristics of these breathing structures can be described by breathing frequency?,maximum breathing amplitudeAand lifetimeτ, which can be manipulated by atomic numberNiand interspecies scattering lengtha12.Meanwhile,the abovementioned breathing structures can undergo quasi-transition processes through appropriate choices ofNianda12.Additionally,the collision of two identical special breathing structures also can bring more abundant breathing dynamics.The results show that two SS or DS structures of the same type can maintain their stability after collision, while the collision of two identical MS structures at different velocities can either extend or shorten their lifetimeτ.Our findings indicate significant differences from the single-component dipolar BECs,thereby enriching the collision dynamics of matter-wave solitons.Furthermore, Our results provide a reference for the study of soliton interactions and deepen the understanding of soliton properties in a binary dipolar BECs.

Acknowledgment

Project supported by the National Natural Science Foundation of China (Grant Nos.12247103, 12275213, and 12247110).