BIFURCATION CONTROL FOR A FRACTIONAL-ORDER DELAYED SEIR RUMOR SPREADING MODEL WITH INCOMMENSURATE ORDERS?
(葉茂林) (蔣海軍)
College of Mathematics and System Sciences, Xinjiang University, Urumqi 830046, China
E-mail: 1733981567@stu.xju.edu.cn; jianghaijunxju@163.com
Abstract A fractional-order delayed SEIR rumor spreading model with a nonlinear incidence function is established in this paper,and a novel strategy to control the bifurcation of this model is proposed.First,Hopf bifurcation is investigated by considering time delay as bifurcation parameter for the system without a feedback controller.Then,a state feedback controller is designed to control the occurrence of bifurcation in advance or to delay it by changing the parameters of the controller.Finally,in order to verify the theoretical results,some numerical simulations are given.
Key words rumor spreading;fractional-order;time delay;bifurcation control
1 Introduction
A rumor is an unsubstantiated exposition or interpretation of a matter,event or issue which the public are interested in spreading through various channels.Nowadays,with the rapid development of science and technology,online social media platforms bring great convenience,but also have accelerated the spread of rumors in social media networks.The form of rumor transmission has changed from the traditional word of mouth to various online social platforms such as Twitter,WeChat,Weibo,etc..Rumors can have a great impact on people’s daily life and on social order [1–3].For example,the report that shuanghuanglian oral liquid could effectively suppress the spread of COVID-19 caused a panic buying phenomenon and resulted in the shortage of drugstores.However,shuanghuanglian oral liquid can only be used to clear heat and for detoxify,and further clinical data are needed to determine whether it can actually effectively suppress COVID-19.This event demonstrates that it is of great practical significance to study the dynamics of rumor propagation in social networks.
Research on the dynamics of rumor propagation dates back to the 1960s.In [4,5],the classic DK model was proposed by Daley and Kendall.It divided the population into three categories–ignorant,spreader and removed– and it used numerical methods similar to those used in the study of infectious diseases to understand the process through which rumors spread.After Daley and Kendall,Maki and Thomson,in 1973,improved the DK model and established the MK model [6].Based on that researches,various compartment models have appeared and been widely used in the study of the rumor propagation process;these include SIR [7,8],SEIR [9],ILSCR [10],etc..In recent years,researchers have continued to improve the rumor propagation model.Wanget al.established a SIR rumor propagation model considering the cross-propagation mechanism in a multi-language environment,then conducted global dynamics analysis and sensitivity analysis on the model [11].Liet al.conducted stability analysis and a sensitivity analysis for the I2S2R rumor propagation model in heterogeneous networks [12].Afassinou analyzed the influence of the education level of social media users on rumor spreading mechanisms [13].
Time delay is a factor that cannot be ignored with regard to rumor propagation;it can be used to help simulate the process by which rumors spread and the process by which governments and social media platforms educate rumor propagators in order to stop spreading rumors[14–17].Functional differential equations provide a dynamic system with infinite dimensions in essence,and the slight change of system parameters may cause a change of equilibrium stability.When the parameters exceed a certain critical value,a branch of periodic orbits can be separated from the equilibrium point and the Hopf bifurcation phenomenon can be generated.For functional differential equations,the delay is generally taken as a parameter,and the condition of bifurcation is considered when the delay changes.In the field of rumor propagation research,Ankuret al.considered the double time delay caused by expert intervention and government control measures and established the 2SI rumor propagation model,and the critical value of expert intervention delay and Hopf bifurcation conditions were obtained through calculation[18].Wanget al.established the I2S2R rumor propagation model with a time delay in a multi-language environment,and obtained the bifurcation conditions of the system [19].
Bifurcation control has become more and more popular in recent years.The purpose of a bifurcation controller is to change the dynamic properties of the original solution of the system by considering a control criterion.Various controllers are designed to control the dynamic behavior of systems;these include the Proportional-Derivative feedback controller [20],the state feedback controller [21]and so on.Chenget al.established a complex network model with time delays,then performed bifurcation analysis on the model and proposed a hybrid control strategy in [22].
Fractional calculus after referred to as generalized calculus or arbitrary calculus is a generalization of integral calculus and has a short-term memory effect and a genetic effect.Fractional differential equations have been used in a wide range of fields[23–26],and mainly includes analysis and synthesis of fractional dynamic systems.Wanget al.established a fraction-order delay SIR epidemic model with saturation incidence and recovery functions and then analyzed the stability of the disease-free equilibrium and disease-prevalence equilibrium of the system[27].In recent years,some scholars considered adding controllers to control the bifurcation that occurrs in fractional systems with a time delay;these include the state feedback controller [28]and the fractional PD controller [29].The influence of a memory effect on information transmission process was considered in [30,37],where it can be seen that multiple redundant contacts of the same rumor will change people’s initial thoughts regarding it,and the cumulative effect will impact upon the behavior of individuals in social networks.Due to the memory effect of fractional calculus,the rumor propagation process can be analyzed accurately by studying the rumor propagation process with fractional calculus.In [38],Singh established a SIR rumor spreading model in a social network with the Atangana-Baleanu derivative:
At the same time,the dynamic behavior of the model was studied.Renet al.investigated a stochastic SIR model in the sense of Caputo’s fractional derivative for rumor spreading in social networks:
The stability of the given model’s equilibrium point was studied in [39].However,fractional differential equations have rarely been used in the study of rumor propagation,which has fended to mainly focus on the application of the SIR rumor model.Based on the above work,combining the nonlinear function and time delay,we establish a fraction-order SEIR rumor model in a homogeneous network and add a feedback controller to control the occurrence of bifurcation in advance or delay by changing the parameters of the controller.
The rest of this article is arranged as follows: in Section 2,some preparations related to fractional equations are introduced.In Section 3,a fraction-order SEIR rumor spreading model is proposed.In Section 4,bifurcation conditions for the uncontrolled system and the controlled system are obtained.Two numerical simulation examples are illustrated in Section 5 in order to verify the theoretical results.In Section 6,a brief summary of the whole paper is presented.
2 Preliminaries
In this section,some preparations related to fractional differential equations are given.
Definition 2.1([31]) The Caputo fractional derivative of orderαof a functionf(x) is defined as
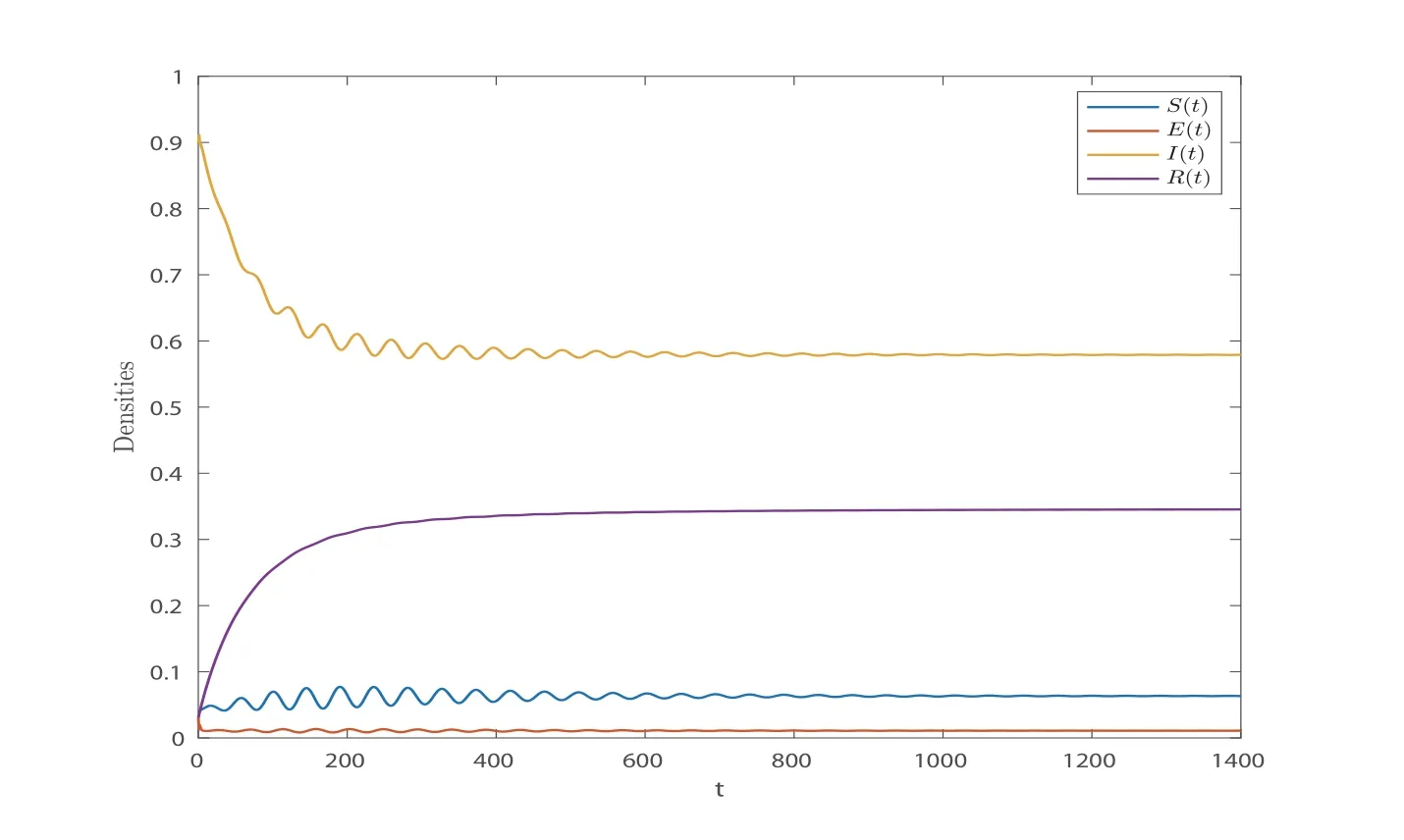
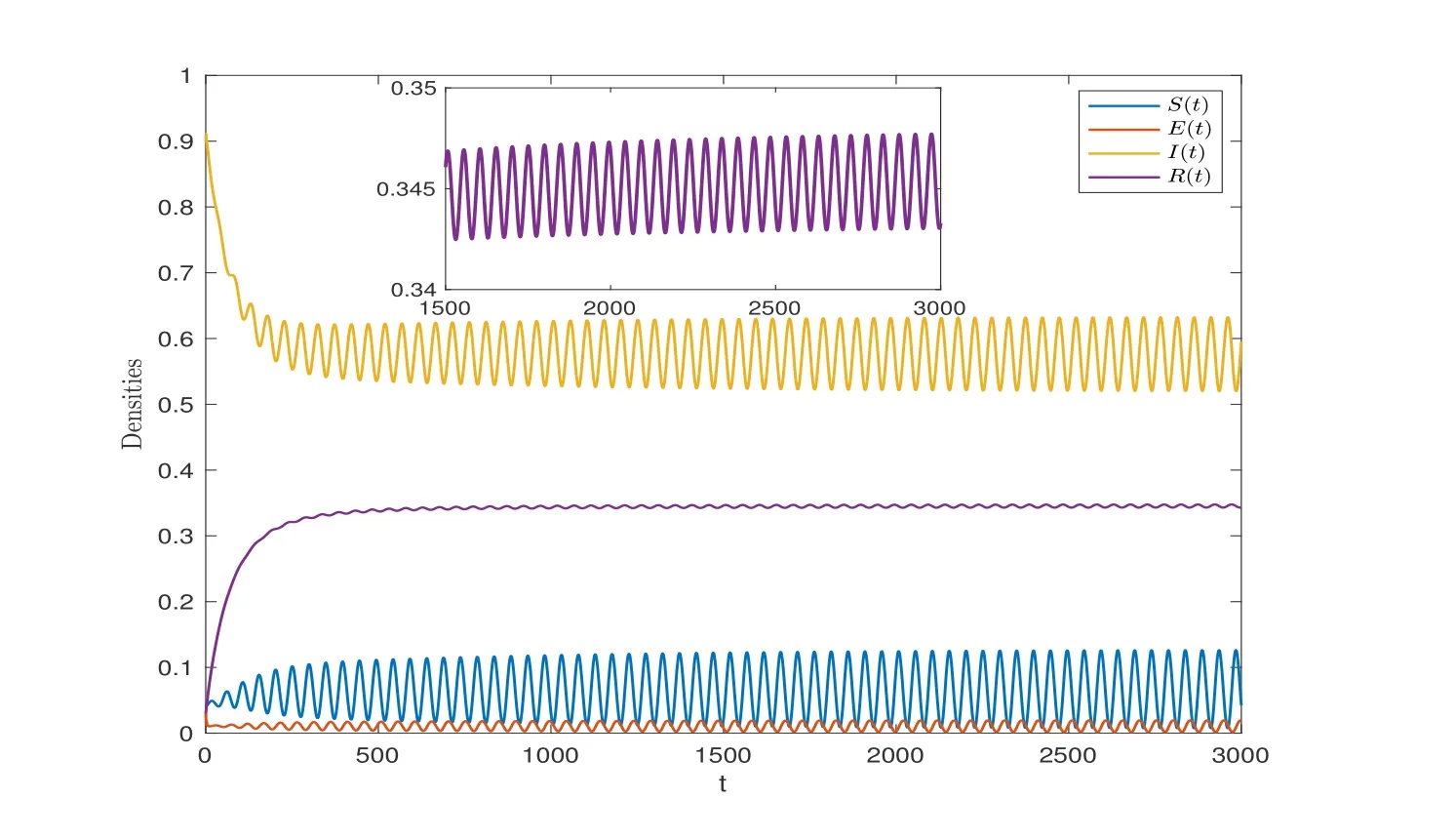
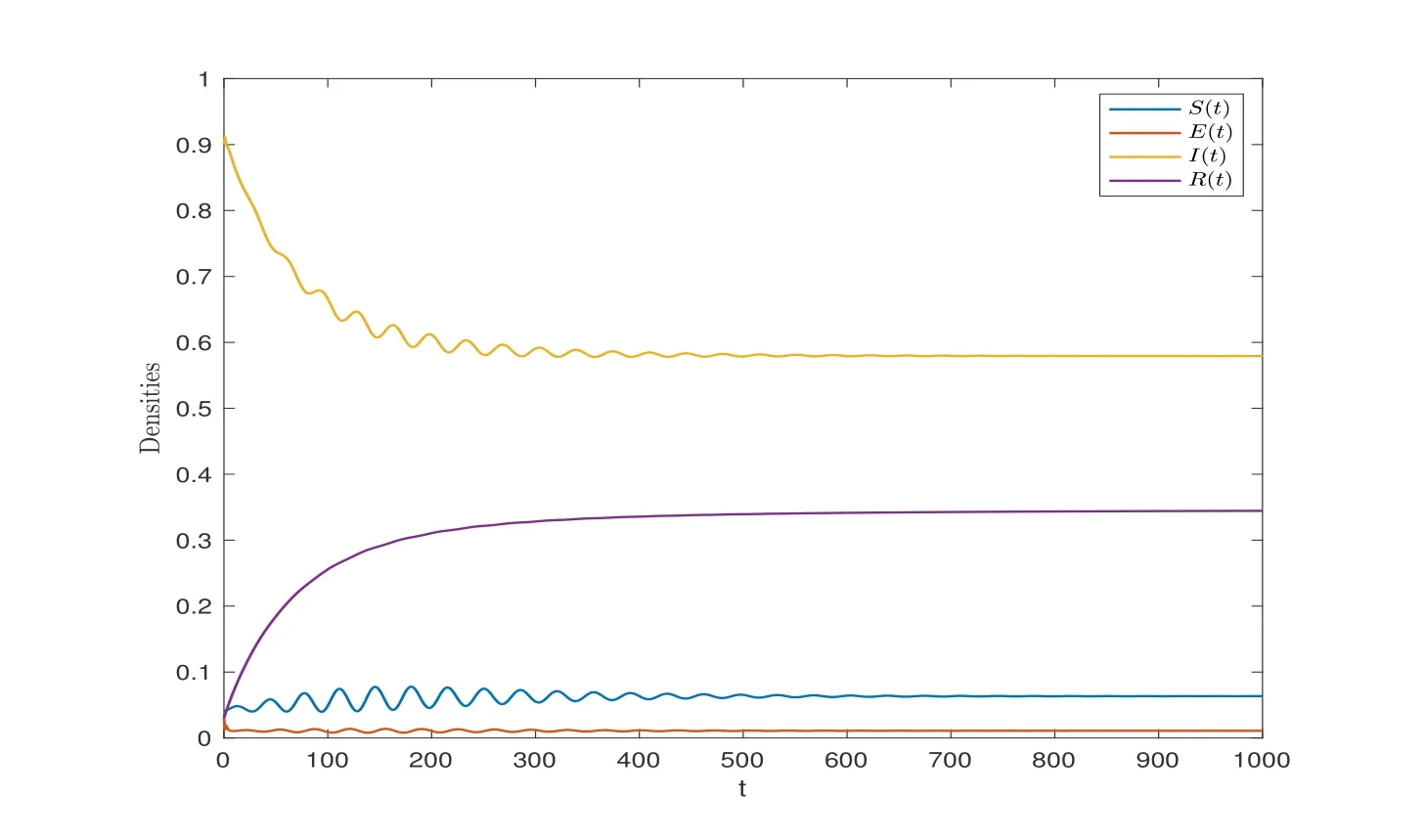
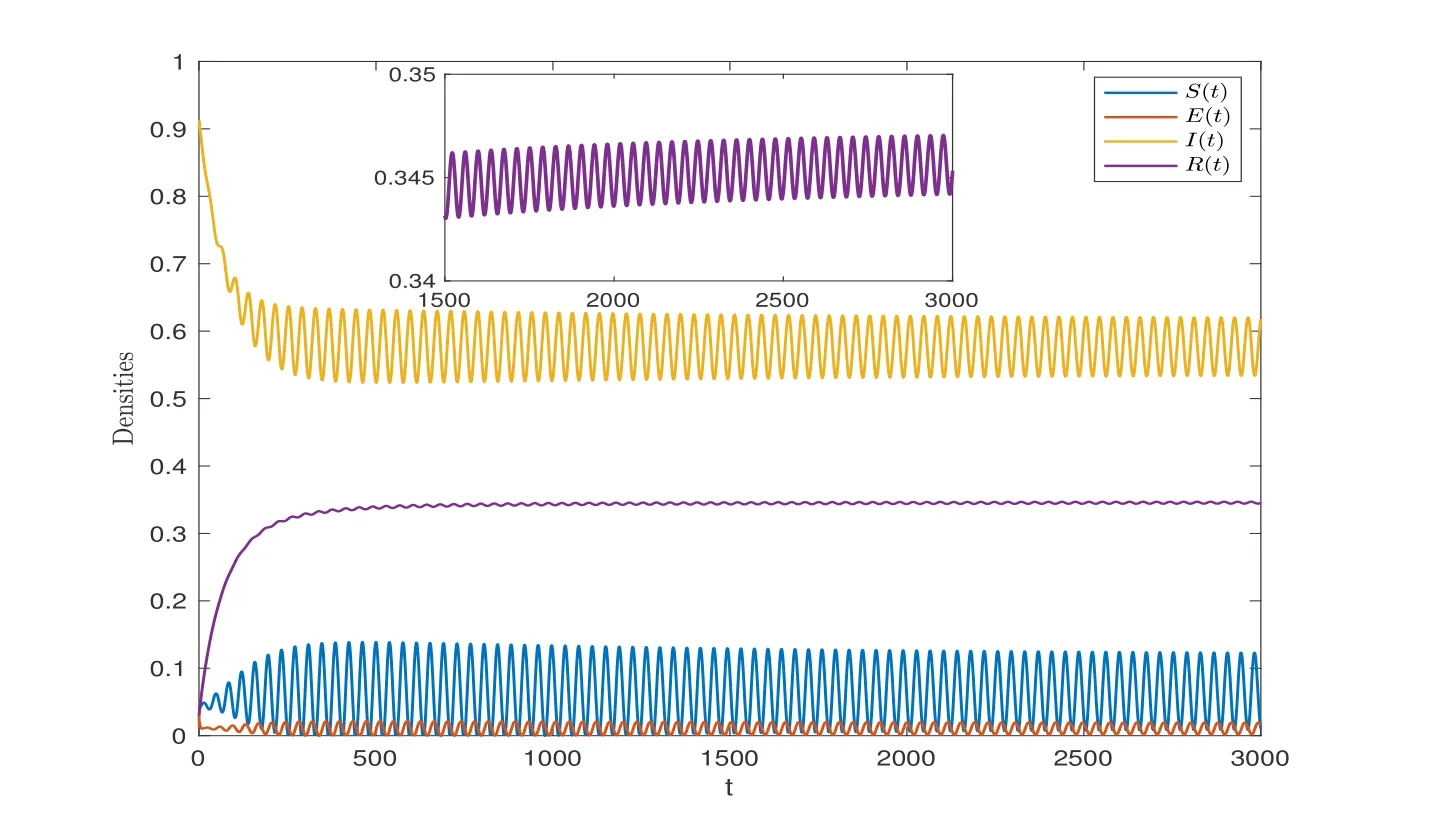
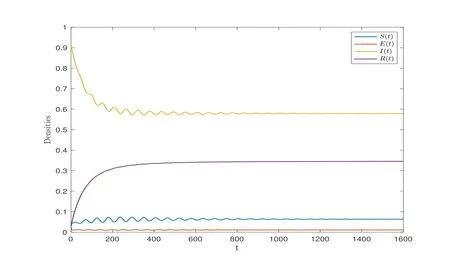
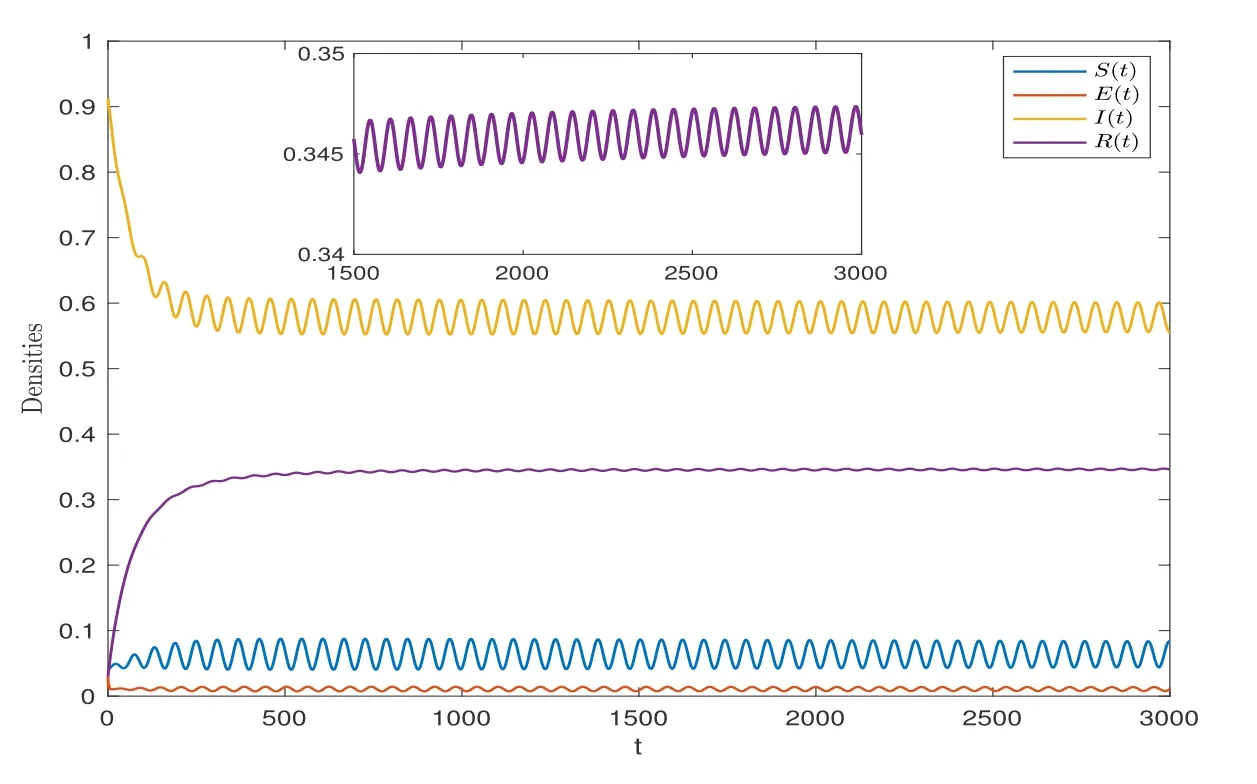
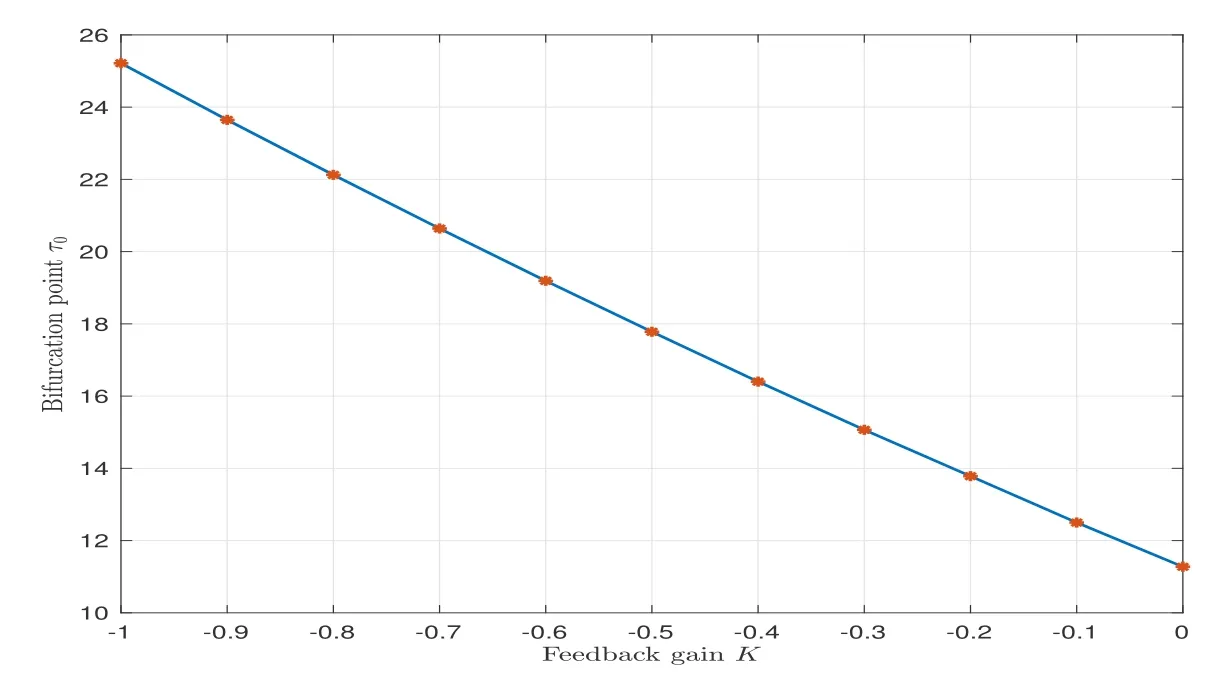
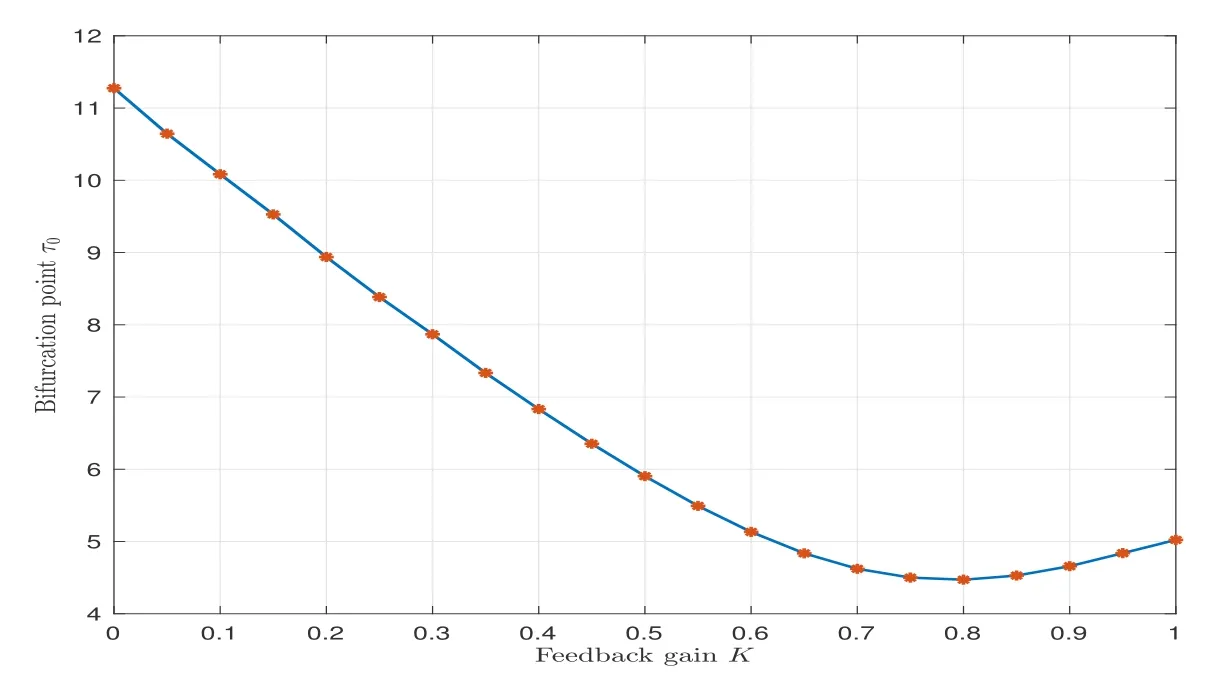
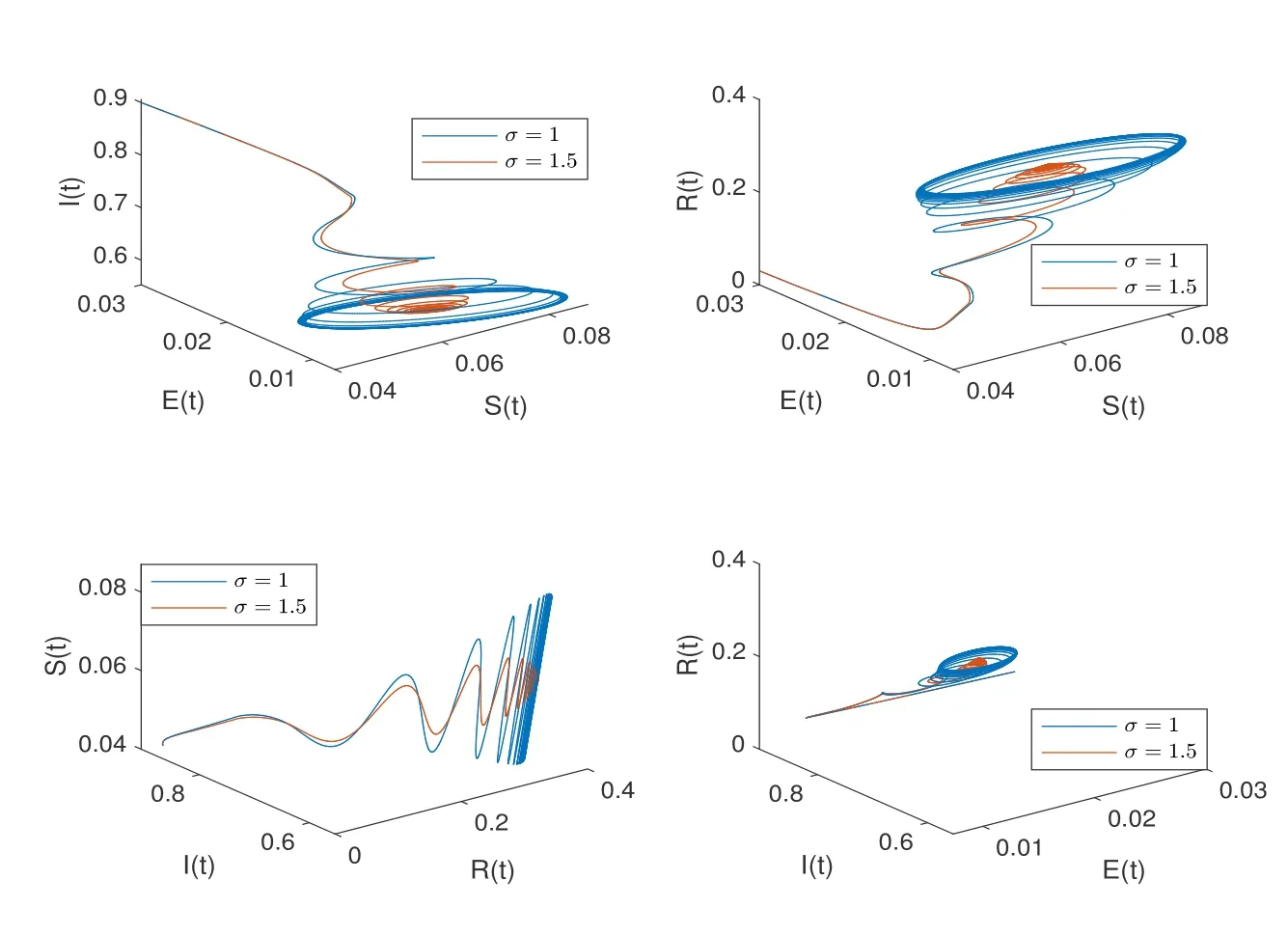
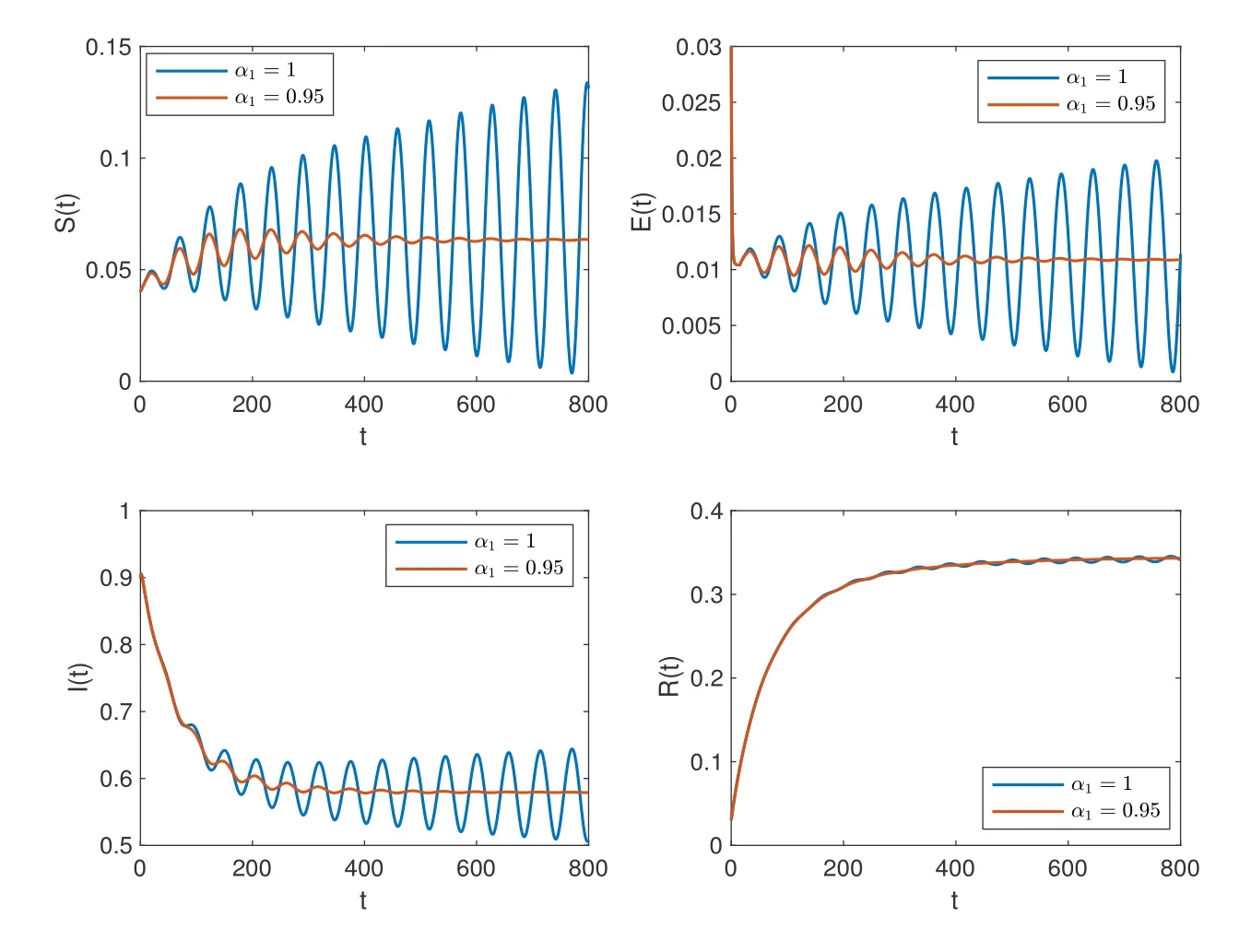
wherenis the positive integer andn-1<α Lemma 2.2([32]) Consider the followingn-dimensional linear fractional differential system with multiple time delays: Hereqiis real and lies in(0,1),the initial valuesxi=φi(t)are given for-maxi,j τij=-τmax≤t ≤0 andi=1,2,···,n.In this system,the time-delay matrix isT=(τij)n×n ∈(R+)n×n,the coefficient matrix isA=(aij)n×n,the state variables arexi(t),xi(t-τij)∈R,and initial values areφi(t)∈C0[-τmax,0].Then,the characteristic matrix of system (2.1) can be presented: Lemma 2.3([32]) Suppose thatτij=0 and that allqisare rational numbers between 0 and 1 fori,j=1,···,n.LetMbe the lowest common multiple of the denominatorsuisofqis,where,(ui,vi)=1,ui,vi ∈Z+,i=1,···,n.Then the zero solution of system (2.1)is Lyapunov globally asymptotically stable if of all the rootsλsof the equation We establish the following fractional-order (0<α1,α2,α3,α4<1) rumor propagation model and study the Hopf bifurcation of the model with time delay: Here we have the initial conditions (H1)〈k〉A(chǔ)βδ-u(δ+u)(θ+u)>0. By using (H1),system (3.1) has a rumor-spreading equilibriumP?(S?,E?,I?,R?),where In this section,the Hopf bifurcation of system (3.1) atP?is studied;hereτis chosen as a bifurcation parameter,and the bifurcation point is identified.Then,after the controller is added to the original system,τis still selected as the bifurcation parameter and a new bifurcation point is obtained. In this subsection,τis chosen as the bifurcation parameter that is used to find the bifurcation point of system (3.1) and to get the conditions of the Hopf bifurcation. By applying Lemma 2.2,the characteristic matrix of system (4.2) at (0,0,0) is expressed as follows: Whenτ=0,the characteristic equation of system (4.2) can be written as From Lemma 2.3,the zero solution of system (4.2) is asymptotically stable when all of solutionλiof the above equation satisfies the condition Whenτ>0,the characteristic equation that corresponds to system (4.2) is Multiplying both sides of eq.(4.3) by eλτ,we have that where Re[mj(iω1)]is the real part ofmj(iω1) and Im[mj(iω1)]is the imaginary part ofmj(iω1)(j=1,2,3).Furthermore, By eq.(4.5),we obtain Squaring both sides of eq.(4.6),we have that Define the bifurcation point whereτ0(k)is defined by eq.(4.8). Remark 4.1In the same way with eq.(4.8),we can also choose the second equation of eq.(4.7) to calculateτ0(k). The following assumption is made to obtain our main results: Here Re[ρ1(iω0)],Im[ρ1(iω0)],Re[υ1(iω0)],Im[υ1(iω0)]are mentioned in eq.(4.10). Lemma 4.2Letλ(τ)=ξ(τ)+iω1(τ) be the root of eq.(4.4) nearτ=τ0satisfying thatξ(τ0)=0,ω1(τ0)=ω0.Then the following condition holds: ProofDifferentiate both sides of eq.(4.4) with respect toτ.Then we get that As a result, where It is deduced from eq.(4.9) that where Re[ρ1(iω0)],Im[ρ1(iω0)]are the real and imaginary parts,respectively,ofρ1(iω0).Re[υ1(iω0)],Im[υ1(iω0)]are the real and imaginary parts,respectively,ofυ1(iω0).Furthermore, Applying (H2) completes the proof. According to Lemmas 2.2 and 2.3,the following results can be obtained: Theorem 4.3Under (H1) and (H2),we have that (1) the equilibriumP?of system (3.1) is asymptotically stable whenτ ∈[0,τ0); (2) the equilibriumP?of system (3.1) is unstable whenτ ∈[τ0,+∞).Furthermore,the uncontrolled system (3.1) undergoes a Hopf bifurcation atP?whenτ=τ0. Remark 4.4The stability definition in the Lyapunov sense shows that for linear systems,if the equilibrium is asymptotically stable,then it must be globally asymptotically stable.However,asymptotic stability is not globally asymptotic stability for nonlinear systems.Furthermore,it can be seen that system (3.1) is locally asymptotically stable in the Lyapunov sense whenτ ∈[0,τ0). In recent years,bifurcation control has become a hot research topic.Feedback controllers are used in many fractional systems.In [28],Wanget al.established the following fractional order eco-epidemiological system Here,a feedback controllerμ(t)=h[I(t)-I(t-ν)]is designed to control the bifurcation behavior of the system with time delayτas the bifurcation parameter.Similarly,Huanget al.established the fractional predator-prey system in [40]: At the same time,an effective extended feedback controlleru(t)=K[x1(t)-x1(t-σ)]can be designed for the above system for controlling the creation of bifurcation.In the field of rumor propagation,Huanget al.established following delay reaction-diffusion malware propagation model in [41] Furthermore,a state feedback controlleru(t)=-k1(I-I?)-k2(I-I?)2-k3(I-I?)3is designed to control the creation of the Hopf bifurcation for the given system.However,there has been little research on the application of the state feedback controller to the fractional rumor propagation model.In this subsection,we design the feedback controller whereσrepresents the feedback controller delay andKdenotes the feedback gain. Remark 4.5In this paper,we only take-1≤K ≤1.It is clear thatη(t)=0 whenK=0 orσ=0. In order to control the bifurcation and make the bifurcation advance or delay,τis chosen as the bifurcation parameter to get the conditions of Hopf bifurcation.The model with a feedback controller is as follows: Here we have the initial conditions By the same linearization treatment as the one mentioned above,the characteristic equation of the controlled system (4.11) can be obtained. Remark 4.6For the sake of the simplicity of the derivation,we linearize the controller separately when linearizing the controlled system (4.11). For convenience,we still just deal with the first three equations.The characteristic matrix of system (4.12) at (0,0,0) is expressed as follows: Hence,the characteristic equation that corresponds to system (4.12) is Multiplying both sides of eq.(4.13) by eλτ,we have that where Re[nj(iω2)]is the real part ofnj(iω2) and Im[nj(iω2)]is the imaginary part ofnj(iω2)(j=1,2,3).Furthermore, By eq.(4.15),we obtain that Squaring both sides of eq.(4.16),we have that Define the bifurcation point whereτ01(k) is defined by eq.(4.18). The following assumption is made to obtain our main results: Lemma 4.7Letλ(τ)=ξ(τ)+iω2(τ)be the root of eq.(4.14)nearτ=satisfying thatThen the following condition holds: ProofDifferentiating both sides of eq.(4.14) with respect toτ,we get As a result, It can be deduced from eq.(4.19) that applying (H3) completes the proof. According to Lemmas 2.2 and 4.7,the following results can be concluded: Theorem 4.8Under (H1) and (H3),we have that (1) the equilibriumP?of system (4.11) is asymptotically stable whenτ ∈[0,); (2) the equilibriumP?of system (4.11) is unstable whenτ ∈[,+∞).Furthermore,the controlled system (4.11) undergoes a Hopf bifurcation atP?whenτ=. Remark 4.9Compared with the results of [19],the ordinary differential equation theory is replaced by the fractional differential equation theory to study the Hopf bifurcation of the rumor spreading model;this is consistent with the memory effect of the rumor spreading process. Remark 4.10Apart from the results of the bifurcation condition in [19],this paper not only conducts a bifurcation analysis for the fractional order rumor propagation model with a time delay,but also adds a state feedback controller and controls the advance or delay of bifurcation by adjusting the controller parameters. Remark 4.11For the selection of a bifurcation controller,differently from the fractional PD controller used in[29],the state feedback controller is simple in design and is easy to operate.More importantly,the state feedback controller has a wide range of applications,including in neural networks [21],eco-epidemiological systems [28]and predator-prey systems [34]. In this section,some numerical simulation examples are given to verify the correctness of the theoretical results.To solve the fractional differential equations,we mainly use a predictorcorrector method which is described in [35,36]. Case 1A specific example for the uncontrolled system (3.1). In this case,A=0.01,〈k〉=3,β=0.09,u=0.01,α=0.1,δ=0.85,θ=0.006,α1=0.99,α2=0.98,α3=0.98,α4=0.95 are selected,and then the specific system is as follows: By a simple calculation,we can obtain the rumor-spreading equilibrium point It is calculated thatω0=0.130,τ0=11.27.Based on Theorem 4.1,theP?of system (5.1)is asymptotically stable whenτ ∈[0,τ0),however,Hopf bifurcation occurs atP?whenτ=τ0.We chooseτ=11.26<11.27 andτ=12.05>11.27.The results are shown in Figures 1 and 2. Case 2A specific example for the controlled system (4.11). In this case,A=0.01,〈k〉=3,β=0.09,u=0.01,α=0.1,δ=0.85,θ=0.006,α1=0.99,α2=0.98,α3=0.98,α4=0.95 are chosen,and then the specific system is as follows: By a simple calculation,we can obtain the rumor-spreading equilibrium Remark 5.1In the process of calculating the equilibrium point of the controlled system(5.2),the added controller does not affect the original state of system (5.1),which means that whateverKandσare,they do not affect the equilibrium of the original system (5.1). Now the influence of controller parameters on bifurcation points studied based on the original uncontrolled system (5.1). First,letK=0.2,σ=1.It is calculated that=0.166,=8.94.Based on Theorem 4.2,theP?of system (5.2) is asymptotically stable whenτ ∈[0,),however,Hopf bifurcation occurs atP?whenτ=.Letτ=8.93<8.94 andτ=9.04>8.94.The results are shown in Figures 3 and 4. Then,letK=-0.21,σ=1.By a simple calculation,we get that=0.105,=13.91.We chooseτ=13.9<13.91 andτ=15.01>13.91.The results are shown in Figures 5 and 6. Furthermore,in order to study the effect of the feedback gainKon the bifurcation pointτ0for system (5.2),we selectσ=1 and takeK ∈[-1,0],K ∈[0,1].We can note that the value of the bifurcation point decreases with the increase ofKwhenK ∈[-1,0],and the value of the bifurcation point decreases first and then increases whenK ∈[0,1].These results are shown in Figures 7 and 8. Remark 5.2When the feedback gain isK<0,the controllerη(t)contributes to the system stability,while the controller has the opposite effect on system stability when the feedback gain isK>0. Next,the influence of a controller delay on the bifurcation points is discussed.We chooseK=0.2 andK=-0.2.Figure 9 shows that the stability of the controlled system(5.2)increases as the feedback delayσincreases whenK=0.2,however,the stability of the controlled system(5.2) decreases as the feedback delayσincreases whenK=-0.2,which can be seen in Figure 10. Figure 1 State trajectories of system (5.1) when τ=11.26<τ0 Figure 2 State trajectories of system (5.1) when τ=12.05>τ0ν Figure 3 State trajectories of system (5.2) when K=0.2, σ=1, τ=8.93< Figure 4 State trajectories of system (5.2) when K=0.2, σ=1, τ=9.04> Figure 5 State trajectories of system (5.2) when K=-0.21, σ=1, τ=13.9< Figure 6 State trajectories of system (5.2) when K=-0.21, σ=1, τ=15.01> Figure 7 Effect of feedback gain K (K ∈[-1,0]) on bifurcation point τ0 for system (5.2) Figure 8 Effect of feedback gain K (K ∈[0,1]) on bifurcation point τ0 for system (5.2) Figure 10 Phase diagrams of system (5.2) with K=-0.2 and τ=15.7 Finally,the effect of the fractional order on system stability is discussed.α2=0.97,α3=0.98 andα4=0.95 are selected.For convenience,only the effect of fractional orderα1is studied.From Figure 11 and Figure 12,it can be seen that the solution of system(5.2)changes from stable to unstable as the fractional order increases,and this is the case whetherK ∈[0,1]orK ∈[-1,0]. Figure 12 State trajectories of system (5.2) with K=-0.15,τ=15,σ=1 Remark 5.3It can be seen from Figure 11 and Figure 12 that the stability of system(5.2)changes while changing the order.Also,the solution of system(5.2)changes from unstable to asymptotically stable as the fractional order decreases.Thus,the order of the fractional differential system can be considered in order to discuss Hopf bifurcation under certain conditions,and these bifurcation conditions will be studied in the future. In this paper,a fractional-order delayed SEIR rumor spreading model with a nonlinear incidence function was analyzed.Fractional order theory was used so as to make the rumor propagation process more accurate.First,we studied the asymptotically stable condition of rumor-spreading equilibrium and a time delay was chosen as a bifurcation parameter to discuss the bifurcation induced by a time delay.Then,we added feedback controllers to the original system in order to control the occurrence of bifurcation in advance or delay.In the numerical simulation,we discussed the influence of the controller parameters and the fractional order on the value of the bifurcation point.With the increase of the fractional order,the value of the bifurcation point increased continuously.Finally,the effect of controller parameters on the value of bifurcation points was discussed.It was shown that the feedback gain and delay of the controller has a great influence on the stability of the controlled system. Conflict of InterestThe authors declare no conflict of interest.3 Description of the Rumor Spreading Model

4 Main Result
4.1 Bifurcation Induced by τ of the Uncontrolled System (3.1)
4.2 Bifurcation Induced by τ of the Controlled System
5 Numerical Simulations
6 Conclusions
 Acta Mathematica Scientia(English Series)2023年6期
Acta Mathematica Scientia(English Series)2023年6期
- Acta Mathematica Scientia(English Series)的其它文章
- THEORETICAL RESULTS ON THE EXISTENCE,REGULARITY AND ASYMPTOTIC STABILITY OF ENHANCED PULLBACK ATTRACTORS:APPLICATIONS TO 3D PRIMITIVE EQUATIONS?
- ENTIRE SOLUTIONS OF LOTKA-VOLTERRA COMPETITION SYSTEMS WITH NONLOCAL DISPERSAL?
- NOTES ON THE LOG-BRUNN-MINKOWSKI INEQUALITY?
- GENERAL CONTENTS
- THE EXISTENCE OF GROUND STATE NORMALIZED SOLUTIONS FOR CHERN-SIMONS-SCHR?DINGER SYSTEMS?
- AN INFORMATIC APPROACH TO A LONG MEMORY STATIONARY PROCESS?
