劉潤(rùn)鳳,胡奇宏,周 芳,程曉迪,王小云,黃勇剛

(吉首大學(xué)物理與機(jī)電工程學(xué)院,湖南 吉首 416000)

密度泛函理論(Density Functional Theory,DFT)能夠準(zhǔn)確描述各種材料的基態(tài)性質(zhì),是計(jì)算凝聚態(tài)物理電子結(jié)構(gòu)的重要方法[1-2].然而,DFT的計(jì)算成本與體系中電子數(shù)量的立方成正比,因此往往僅能用于處理具有周期結(jié)構(gòu)或者超小規(guī)模的體系,而對(duì)于大規(guī)模多電子體系,DFT的應(yīng)用受到極大限制.相比之下,無(wú)軌道密度泛函理論(Orbital-Free Density Functional Theory,OF-DFT)的計(jì)算成本較低,其實(shí)質(zhì)可以看作是只考慮最小特征值的自恰Kohn-Sham方程[3-6],能直接通過(guò)電子密度計(jì)算總能量,因此可以突破DFT在模擬尺度上的極限.OF-DFT的主要優(yōu)點(diǎn)是線(xiàn)性縮放計(jì)算成本,可應(yīng)用于非常大的系統(tǒng).此外,在有限元方法中實(shí)施OF-DFT,進(jìn)一步擴(kuò)展了OF-DFT的應(yīng)用廣泛性[7].將OF-DFT與有限元方法結(jié)合,可以實(shí)現(xiàn)對(duì)各種具有復(fù)雜形貌特征的金屬體系的基態(tài)性質(zhì)的精確計(jì)算.基于此,筆者擬采用OF-DFT對(duì)金屬鈉板基態(tài)性質(zhì)進(jìn)行深入探討.

使用OF-DFT計(jì)算體系的基態(tài)密度和功函數(shù)時(shí),能量泛函的選擇至關(guān)重要,它直接影響方法的準(zhǔn)確度.能量泛函由動(dòng)能泛函和交換關(guān)聯(lián)泛函組成,目前相關(guān)研究工作中,許多近似的動(dòng)能泛函被用于描述體系的相互作用能[4-5,8-10].最常采用的動(dòng)能泛函是由Thomas-Fermi (TF) 和von Weizsacker (vW)組合而成的TFvW動(dòng)能泛函,交換關(guān)聯(lián)泛函通常采用基于局域密度近似(Local Density Approximation,LDA)的交換關(guān)聯(lián)勢(shì)[7,11-12].雖然TFvW動(dòng)能泛函被廣泛采用,但vW動(dòng)能泛函缺乏微觀(guān)對(duì)應(yīng),其比重尚未確定.研究發(fā)現(xiàn),vW動(dòng)能泛函的比重越大,電子溢出效應(yīng)越明顯,溢出功也越大[13],因此確定vW動(dòng)能泛函的比重成為一個(gè)亟待解決的問(wèn)題.另外,雖然不同的LDA交換關(guān)聯(lián)勢(shì)被廣泛采用[7],但其對(duì)計(jì)算結(jié)果的影響尚不明確.

為了確定金屬鈉板獲得準(zhǔn)確基態(tài)性質(zhì)所需的vW動(dòng)能泛函,筆者首先研究了OF-DFT及DFT的相關(guān)理論和模型,并介紹了計(jì)算基態(tài)密度和功函數(shù)的方法,進(jìn)一步研究了vW動(dòng)能泛函的比重在不同LDA交換關(guān)聯(lián)泛函中對(duì)基態(tài)密度誤差與功函數(shù)誤差的影響.

1 理論與模型

1.1 無(wú)軌道密度泛函理論

在OF-DFT中,通常通過(guò)求解歐拉方程來(lái)獲得體系的基態(tài)性質(zhì)[4-5,14-15],即

(1)

其中:n表示基態(tài)密度;φ0表示靜電勢(shì);μ表示化學(xué)勢(shì).能量方程G[n]包含電子系統(tǒng)相互作用的動(dòng)能(Ts)和交換相關(guān)能(EXC),即

G[n]=Ts[n]+EXC[n].

(2)

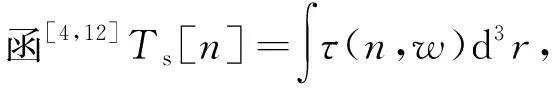
τ(n,w)=τvW(n,w)+τTF(n),

其中

τvW(n,w)=An-1w,

τTF[n]=Bn5/3.

為了求解(1)式,對(duì)方程式兩側(cè)做梯度運(yùn)算,即

(3)

其中E0表示靜電場(chǎng).(3)式稱(chēng)為量子流體動(dòng)力學(xué)靜態(tài)方程.將(3)式與Maxwell方程耦合,可得

(4)

其中n+表示正電荷密度.在凝膠模型中,正電荷密度在球體內(nèi)是均勻恒定的,而在球體邊緣外部突然下降至0.將(3)式與(4)式結(jié)合,可得

(5)

通過(guò)(5)式可以計(jì)算體系的基態(tài)密度.本研究中,所有的OF-DFT計(jì)算都使用有限元(FEM)軟件COMSOL的弱形式模塊來(lái)實(shí)現(xiàn).

1.2 OF-DFT中能量泛函對(duì)基態(tài)性質(zhì)的影響

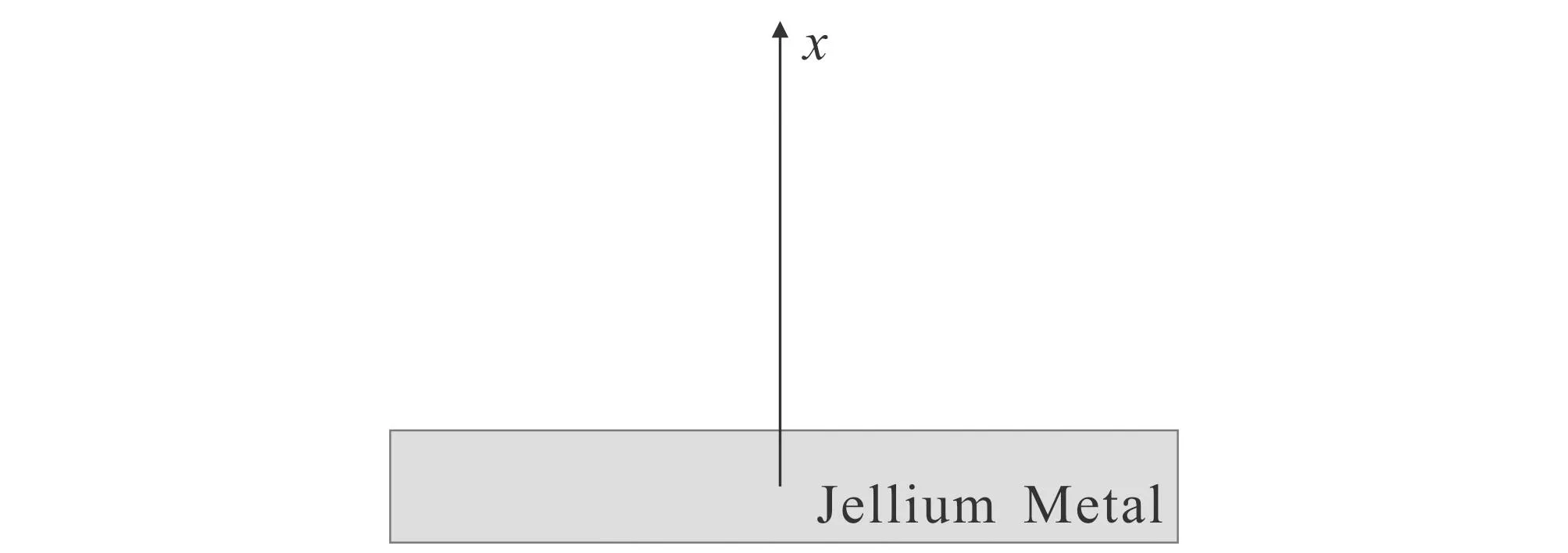
圖1 金屬鈉無(wú)限大平板示意Fig. 1 Schematic Diagram of an Infinite Plate of Sodium Metal

使用OF-DFT計(jì)算金屬鈉無(wú)限大平板的基態(tài)密度和功函數(shù),并將結(jié)果與DFT計(jì)算結(jié)果進(jìn)行對(duì)比.假定無(wú)限大平面在y軸和z軸方向無(wú)限大,在x軸方向的厚度為L(zhǎng),那么本研究只需關(guān)注無(wú)限大平面在x軸方向上的基態(tài)性質(zhì)即可.金屬鈉無(wú)限大平板模型如圖1所示.

首先研究OF-DFT中不同能量泛函對(duì)基態(tài)密度和功函數(shù)的影響.圖2和圖3的縱軸使用對(duì)數(shù)坐標(biāo),這可以明顯比較基態(tài)密度在金屬邊界處的衰減速度.不同vW動(dòng)能泛函比重對(duì)基態(tài)密度的影響如圖2所示.圖2中,交換關(guān)聯(lián)勢(shì)均使用了LDA-WG.從圖2可知,隨著λ的逐漸增大,基態(tài)密度的衰減速度逐漸降低.在對(duì)數(shù)坐標(biāo)下,基態(tài)密度在金屬邊界處的衰減近似為穩(wěn)定的直線(xiàn),這說(shuō)明基態(tài)密度在金屬表面的衰減可以看作近似e指數(shù)衰減[11].vW動(dòng)能泛函的比重可以調(diào)控這一衰減因子,vW動(dòng)能泛函比重越大,衰減因子越小,則基態(tài)密度在金屬邊界處的衰減速度越慢,體系的溢出效應(yīng)越明顯.不同LDA交換關(guān)聯(lián)勢(shì)對(duì)基態(tài)密度的影響如圖3所示.圖3中,參數(shù)vW動(dòng)能泛函比重取值為1.從圖3可知,由LDA-WG,LDA-PZ和LDA-GL計(jì)算得到的基態(tài)密度幾乎沒(méi)有明顯區(qū)別,即使使用了對(duì)數(shù)坐標(biāo),差距仍然較小.

以上結(jié)果說(shuō)明,vW動(dòng)能泛函的比重會(huì)影響基態(tài)密度的計(jì)算結(jié)果.vW動(dòng)能泛函比重的增加,實(shí)質(zhì)上可以理解為增加了體系的電子溢出效應(yīng),因此基態(tài)密度的衰減速度也會(huì)受到影響.相比之下,選擇不同的LDA交換關(guān)聯(lián)勢(shì)對(duì)基態(tài)密度的影響較小.

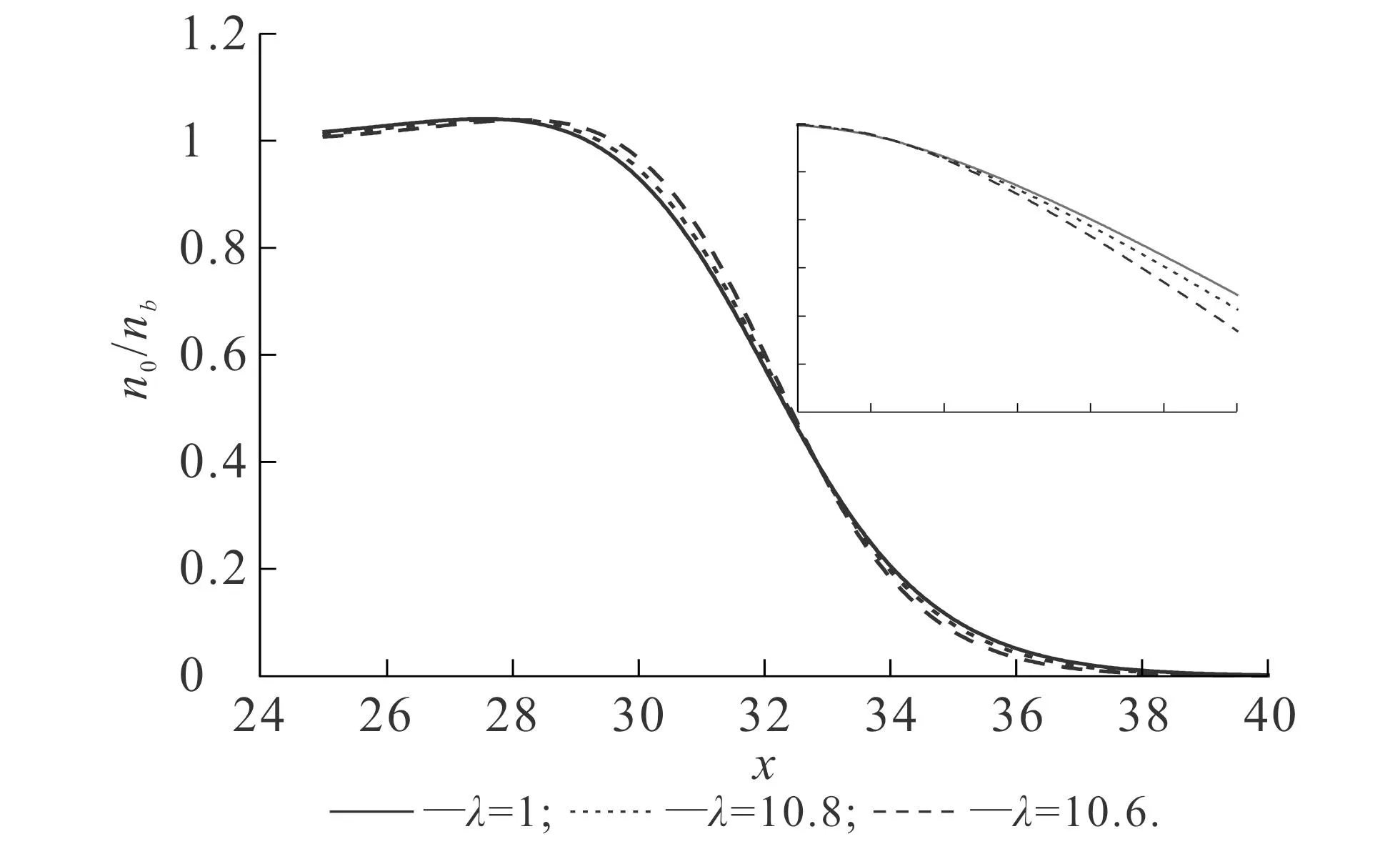
圖2 不同vW動(dòng)能泛函比重對(duì)基態(tài)密度的影響Fig. 2 Ground State Densities Obtained with Different vW Kinetic Energy Functional Proportions

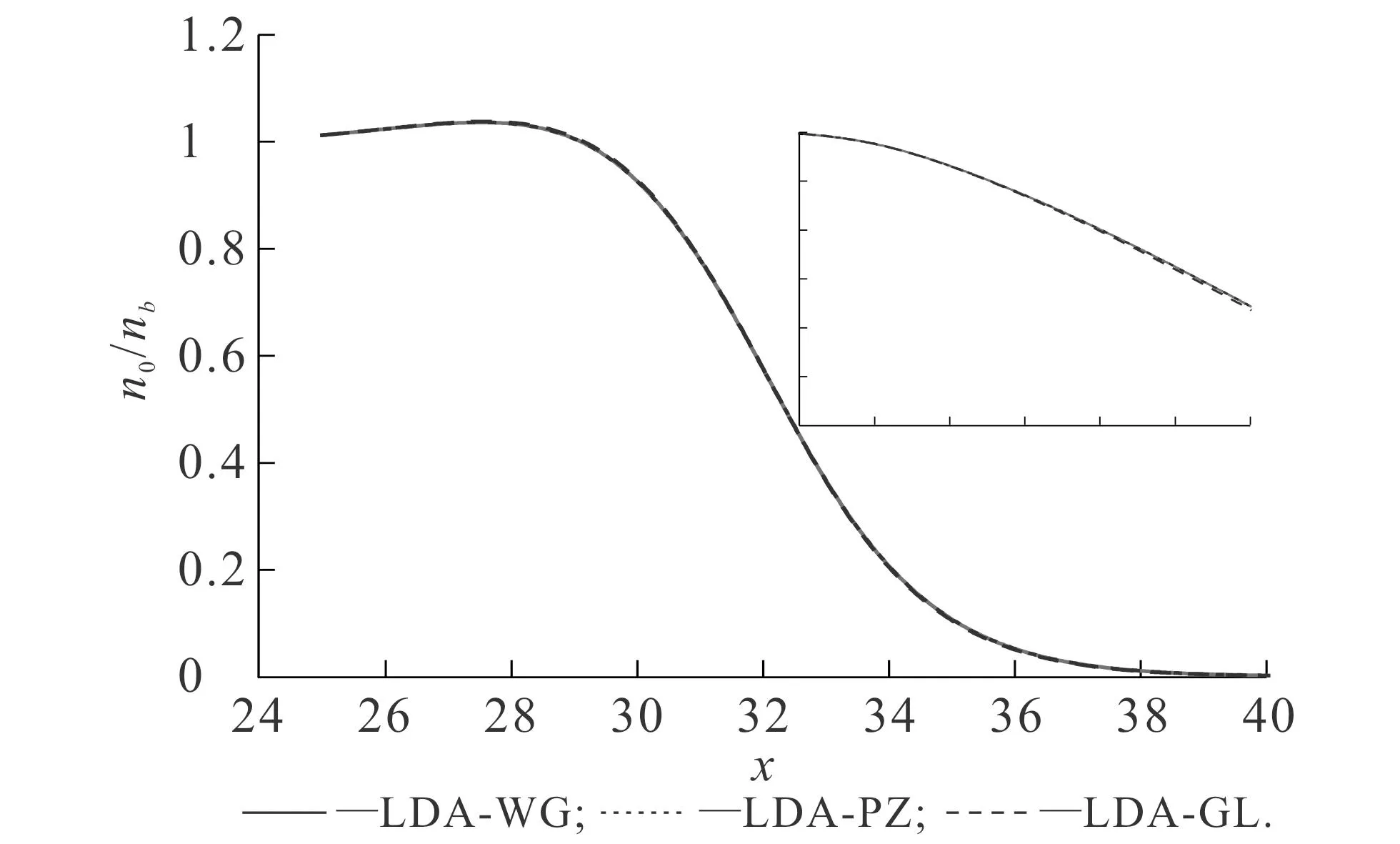
圖3 不同LDA交換關(guān)聯(lián)勢(shì)對(duì)基態(tài)密度的影響 Fig. 3 Ground State Densities Obtained with Different LDA Exchange-Correlation Potentials

另一方面,功函數(shù)同樣是重要的基態(tài)性質(zhì).接下來(lái)筆者介紹使用OF-DFT求解功函數(shù)的方法.OF-DFT可以看作是只考慮最小特征值的自恰Kohn-Sham方程,由于OF-DFT中只考慮最小的特征值,體系中所有電子能量相同,因此(1)式中的化學(xué)勢(shì)(μ)即為體系功函數(shù),即

W=Ts[n]+EXC[n].

(6)

根據(jù)功函數(shù)的定義,(6)式需取無(wú)窮遠(yuǎn)處的值.利用(6)式計(jì)算得到的化學(xué)式,其在空間各處皆為常數(shù).不同vW動(dòng)能泛函比重對(duì)功函數(shù)的影響如圖4所示.圖4中交換關(guān)聯(lián)勢(shì)均使用了LDA-WG.從圖4可知,功函數(shù)隨著λ的增大而增大,λ由0.6增大至1.0時(shí),功函數(shù)由3.218 eV增大至3.538 eV.不同交換關(guān)聯(lián)勢(shì)對(duì)功函數(shù)的影響如圖5所示.圖5中,參數(shù)vW動(dòng)能泛函比重值為1.由圖5可知,LDA-WG,LDA-PZ和LDA-GL計(jì)算得到的功函數(shù)分別為3.538,3.478,3.368 eV.

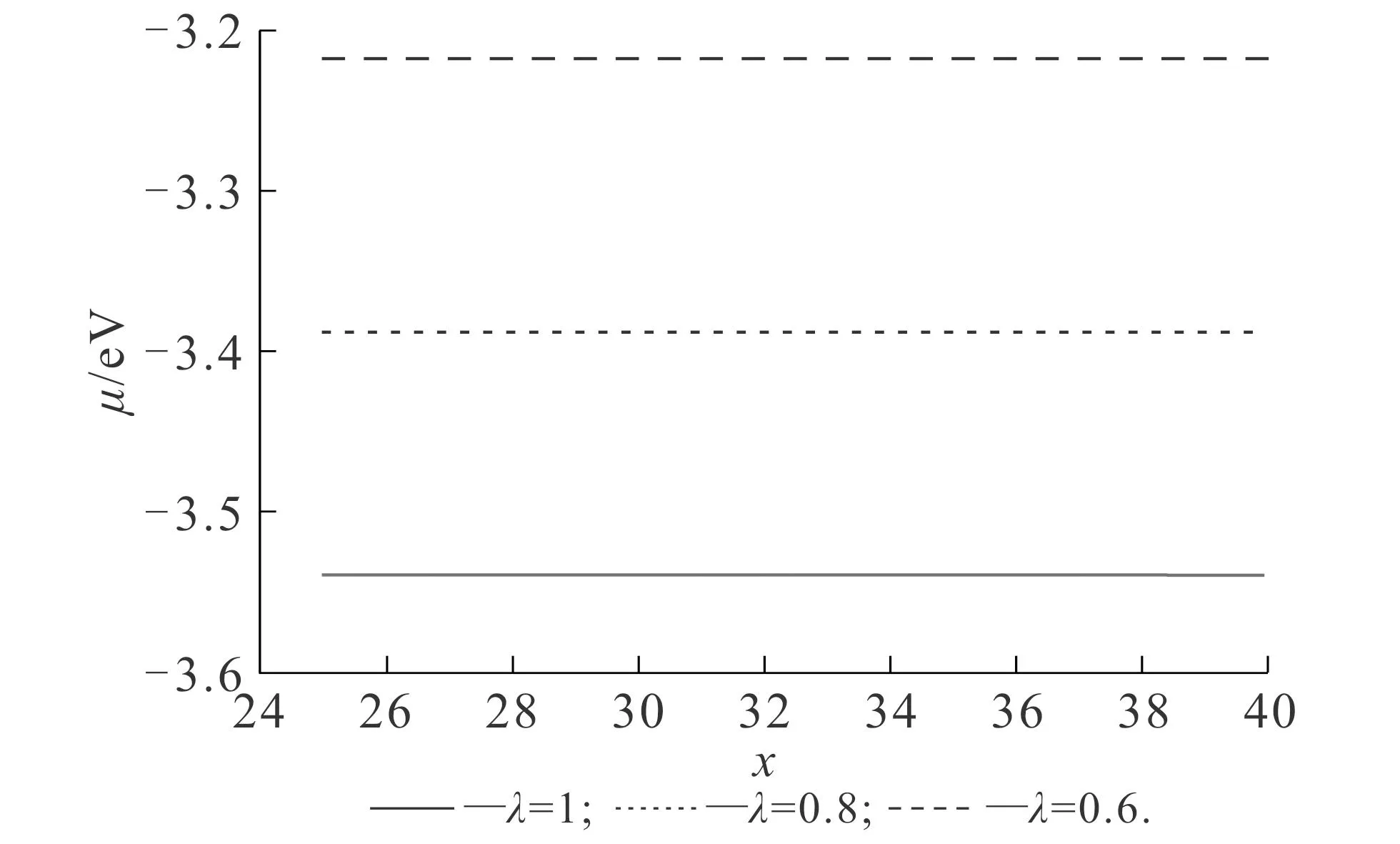
圖4 不同vW動(dòng)能泛函比重對(duì)功函數(shù)的影響Fig. 4 Work Functions Obtained by Different vW Kinetic Energy Functional Proportions

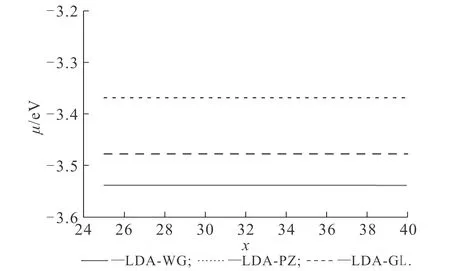
圖5 不同LDA交換關(guān)聯(lián)勢(shì)對(duì)功函數(shù)的影響Fig. 5 Work Functions Obtained by Different LDA Exchange-Correlation Potentials

計(jì)算結(jié)果說(shuō)明,vW動(dòng)能泛函比重和交換關(guān)聯(lián)勢(shì)的改變都會(huì)影響功函數(shù)的計(jì)算結(jié)果.與上述基態(tài)密度的變化類(lèi)似,vW動(dòng)能泛函比重的增加,實(shí)質(zhì)上可以理解為增加體系的電子溢出效應(yīng),從而引起功函數(shù)增加.此外,筆者發(fā)現(xiàn),與基態(tài)密度不同,交換關(guān)聯(lián)勢(shì)的改變會(huì)影響功函數(shù)的計(jì)算結(jié)果,原因在于交換關(guān)聯(lián)勢(shì)在遠(yuǎn)場(chǎng)起主要作用.

1.3 密度泛函理論

為了驗(yàn)證OF-DFT計(jì)算結(jié)果的準(zhǔn)確性,使用開(kāi)源軟件OCTOPUS計(jì)算DFT模塊[16-17],并將DFT計(jì)算結(jié)果與OF-DFT計(jì)算結(jié)果進(jìn)行對(duì)比.在堿金屬中,價(jià)電子的費(fèi)米波長(zhǎng)遠(yuǎn)大于金屬晶格常數(shù),離子的贗勢(shì)對(duì)電子結(jié)構(gòu)沒(méi)有顯著影響.因此,可以用均質(zhì)的正電荷背景代替離散的離子結(jié)構(gòu),即使用凝膠模型[18-20].此時(shí),金屬板鈉體系可以看作是Wigner-Seitz半徑(rs)為4的凝膠模型,進(jìn)一步求解Kohn-Sham方程,這一處理能極大節(jié)省計(jì)算資源.在OCTOPUS中,可以使用不同的交換關(guān)聯(lián)勢(shì),為了能與動(dòng)能泛函在OF-DFT中的作用進(jìn)行比較,本研究使用與OF-DFT一致的交換關(guān)聯(lián)勢(shì).

DFT中,不同LDA交換關(guān)聯(lián)勢(shì)下基態(tài)密度計(jì)算結(jié)果如圖6所示.從圖6可知,與OF-DFT類(lèi)似,DFT中使用不同交換關(guān)聯(lián)勢(shì)計(jì)算得到的基態(tài)密度并無(wú)較大差別.不同LDA交換關(guān)聯(lián)勢(shì)下功函數(shù)計(jì)算結(jié)果如圖7所示.這類(lèi)計(jì)算在文獻(xiàn)[21-23]中已出現(xiàn)過(guò).從圖7可知,功函數(shù)呈現(xiàn)振蕩行為,其原因在于隨著平板厚度的逐漸增加,閑帶的能量逐漸變低,在一定的平板寬度上,各自的最低閑帶接觸并最終穿過(guò)費(fèi)米曲面.這些接觸點(diǎn)以λF/2的周期出現(xiàn)(λF≈3.27rs),筆者觀(guān)察到,功函數(shù)在λF=8時(shí)基本達(dá)到穩(wěn)定振蕩.若進(jìn)一步增加平板厚度,則需要更多的計(jì)算資源,同時(shí)會(huì)導(dǎo)致收斂困難,因此在本研究中,選擇λF=9.5和λF=10時(shí)的平均值作為DFT計(jì)算得到的功函數(shù),這一方案獲得的研究結(jié)果與文獻(xiàn)[14]完全一致.使用LDA-WG,LDA-PZ和LDA-GL交換關(guān)聯(lián)勢(shì)計(jì)算得到的功函數(shù)分別為3.051,2.910和3.025 eV,這說(shuō)明交換關(guān)聯(lián)勢(shì)對(duì)功函數(shù)依然有較大影響.

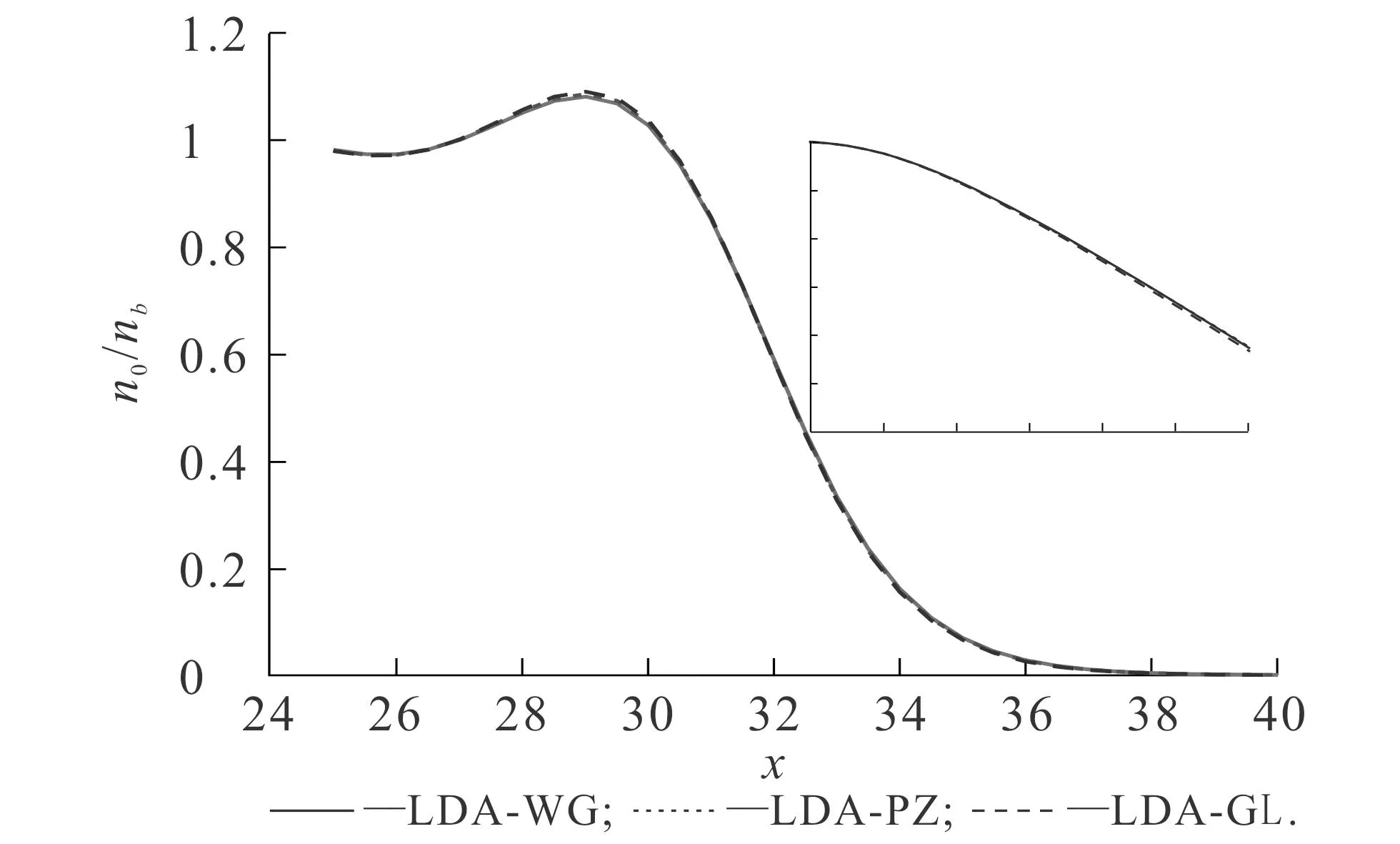
圖6 DFT中不同LDA交換關(guān)聯(lián)勢(shì)對(duì)基態(tài)密度的影響Fig. 6 Ground State Density Calculated for Different LDA Exchange-Correlation Potentials in DFT

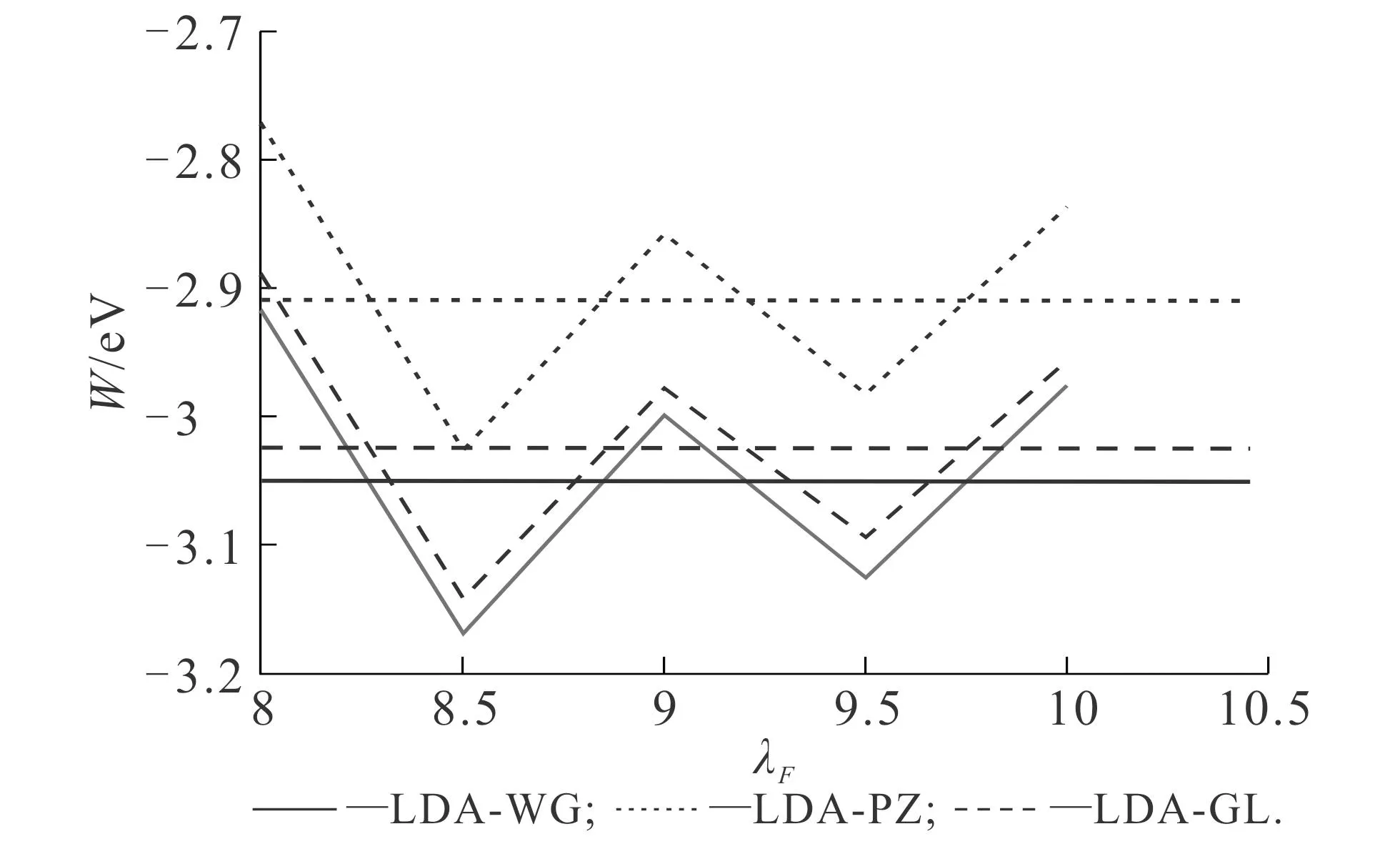
圖7 DFT中不同LDA交換關(guān)聯(lián)勢(shì)對(duì)功函數(shù)的影響Fig. 7 Work Function Calculated for Different LDA Exchange-Correlation Potentials in DFT

1.4 功函數(shù)誤差和基態(tài)密度誤差

筆者計(jì)算了不同動(dòng)能泛函的基態(tài)密度誤差[4],計(jì)算公式為

(7)

其中S表示任意選擇的有限表面積,方程右側(cè)分母表示有限體積中的電子總數(shù).(7)式中的基態(tài)密度誤差可以看作是單個(gè)電子的平均基態(tài)密度誤差.功函數(shù)誤差

其中i=1,2,3,代表3種不同的相關(guān)勢(shì),即WG,PZ,GL相關(guān)勢(shì).需要注意的是,在對(duì)比中要保持選擇的交換關(guān)聯(lián)勢(shì)一致.下面筆者將重點(diǎn)比較OF-DFT中不同動(dòng)能泛函的功函數(shù)誤差與基態(tài)密度誤差,探尋金屬板鈉體系的最優(yōu)能量泛函.

2 誤差最小的能量泛函

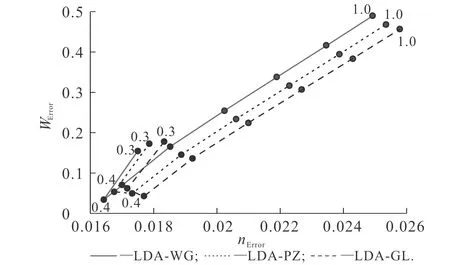
圖8 TFvW動(dòng)能泛函中不同vW動(dòng)能泛函比重對(duì)基態(tài) 密度誤差及功函數(shù)誤差的影響Fig. 8 Ground State Density Error and Work Function Error Obtained by Different vW Kinetic Energy Functional Proportions

不同vW動(dòng)能泛函比重下的基態(tài)密度誤差與功函數(shù)誤差計(jì)算結(jié)果如圖8所示.圖8中包含了LDA-WG,LDA-PZ和LDA-GL 3種交換關(guān)聯(lián)勢(shì),點(diǎn)線(xiàn)旁的數(shù)字代表vW動(dòng)能泛函的比重.例如:LDA-WG交換關(guān)聯(lián)勢(shì)中,數(shù)字1.0代表vW動(dòng)能泛函的比重為1.0,該點(diǎn)橫坐標(biāo)值為0.024 9,縱坐標(biāo)值為0.487,分別對(duì)應(yīng)這一能量泛函下的基態(tài)密度誤差和功函數(shù)誤差.圖8中,vW動(dòng)能泛函的比重由0.3增加至1.0,相鄰點(diǎn)之間的差距為0.1.

對(duì)于LDA-WG交換關(guān)聯(lián)勢(shì),隨著vW動(dòng)能泛函比重的增加,基態(tài)密度誤差先減小后增加,由0.017 5(vW動(dòng)能泛函比重為0.3時(shí))減小至最小值0.016 4(vW動(dòng)能泛函比重為0.4時(shí)),最后上升至0.024 9.使用LDA-PZ和LDA-GL交換關(guān)聯(lián)勢(shì)計(jì)算得到的基態(tài)密度誤差趨勢(shì)與LDA-WG交換關(guān)聯(lián)勢(shì)的基本一致.其中LDA-PZ交換關(guān)聯(lián)勢(shì)的基態(tài)密度誤差由0.017 9下降至0.016 8,最后上升至0.025 4;LDA-GL交換關(guān)聯(lián)勢(shì)的基態(tài)密度誤差由0.018 3下降至0.017 1,最后上升至0.025 8.3種交換關(guān)聯(lián)勢(shì)的基態(tài)密度誤差最小值點(diǎn)均出現(xiàn)在vW動(dòng)能泛函比重為0.4時(shí).對(duì)于功函數(shù),使用3種交換關(guān)聯(lián)勢(shì)計(jì)算得到的功函數(shù)誤差同樣隨vW動(dòng)能泛函比重的增加,呈現(xiàn)出先減小后增加的趨勢(shì).使用LDA-WG,LDA-PZ和LDA-GL交換關(guān)聯(lián)勢(shì)計(jì)算得到的功函數(shù)誤差最小值分別為0.035,0.051,0.043 eV,分別出現(xiàn)在vW動(dòng)能泛函比重為0.4,0.5,0.5時(shí).當(dāng)vW動(dòng)能泛函比重為1時(shí),使用LDA-WG,LDA-PZ和LDA-GL交換關(guān)聯(lián)勢(shì)計(jì)算得到的功函數(shù)誤差分別上升至0.487,0.467,0.456 eV.

以上結(jié)果說(shuō)明,TFvW動(dòng)能泛函中,vW動(dòng)能泛函比重對(duì)基態(tài)密度誤差和功函數(shù)誤差均有較大的影響.原因主要是,隨著vW動(dòng)能泛函比重增加,OF-DFT計(jì)算得到的功函數(shù)增加,基態(tài)密度的衰減速度降低.此外,盡管交換關(guān)聯(lián)勢(shì)對(duì)功函數(shù)有較大影響,比如當(dāng)vW動(dòng)能泛函比重為1時(shí),LDA-WG,LDA-GL和LAD-PZ交換關(guān)聯(lián)勢(shì)的功函數(shù)分別為3.538,3.478,3.368 eV,但對(duì)于相同的動(dòng)能泛函,使用3種交換關(guān)聯(lián)勢(shì)計(jì)算得到的功函數(shù)誤差卻相差不大,比如當(dāng)vW動(dòng)能泛函比重為1.0時(shí),LDA-WG,LDA-PZ和LDA-GL的功函數(shù)誤差分別為0.487,0.467,0.456 eV.原因在于,作為參考值的DFT計(jì)算結(jié)果同樣受交換關(guān)聯(lián)勢(shì)的較大影響.研究結(jié)果進(jìn)一步說(shuō)明,vW動(dòng)能泛函比重為0.4的TFvW能夠適配不同的LDA交換關(guān)聯(lián)勢(shì).

3 結(jié)論

本研究以DFT的計(jì)算結(jié)果作為參考值,計(jì)算了OF-DFT在金屬板鈉體系中獲得準(zhǔn)確基態(tài)密度和功函數(shù)所需的能量泛函.在DFT和OF-DFT中,不同交換關(guān)聯(lián)勢(shì)的使用對(duì)基態(tài)密度的影響較小,而對(duì)功函數(shù)有較大影響,這是因?yàn)榻粨Q關(guān)聯(lián)勢(shì)主要在遠(yuǎn)場(chǎng)起作用.此外,OF-DFT中,vW動(dòng)能泛函比重同時(shí)影響基態(tài)密度和功函數(shù)結(jié)果,因此找到合適的vW動(dòng)能泛函比重至關(guān)重要.筆者定義了OF-DFT的基態(tài)密度誤差與功函數(shù)誤差,通過(guò)數(shù)值實(shí)驗(yàn)發(fā)現(xiàn),vW動(dòng)能泛函比重取0.4時(shí),利用不同LDA交換關(guān)聯(lián)勢(shì)計(jì)算得到的結(jié)果具有較短高的準(zhǔn)確度.值得注意的是,對(duì)于功函數(shù),作為參考值的DFT計(jì)算結(jié)果受到交換關(guān)聯(lián)勢(shì)的影響,在vW動(dòng)能泛函比重為0.4時(shí),不同交換關(guān)聯(lián)勢(shì)的基態(tài)密度誤差和功函數(shù)誤差較小,這說(shuō)明vW動(dòng)能泛函比重為0.4的TFvW能夠適配不同的交換關(guān)聯(lián)勢(shì).因此,vW動(dòng)能泛函比重為0.4時(shí),OF-DFT能給出與DFT較符合的基態(tài)性質(zhì).OF-DFT無(wú)需計(jì)算單粒子波函數(shù),計(jì)算高效,能應(yīng)用到更大尺寸的復(fù)雜納米結(jié)構(gòu)中.