Distributed Optimal Formation Control for Unmanned Surface Vessels by a Regularized Game-Based Approach
Jun Shi and Maojiao Ye ,,
Dear Editor,
This letter explores optimal formation control for a network of unmanned surface vessels (USVs).By designing an individual objective function for each USV, the optimal formation problem is transformed into a noncooperative game.Under this game theoretic framework, the optimal formation is achieved by seeking the Nash equilibrium of the regularized game.A modular structure consisting of a distributed Nash equilibrium seeker and a regulator is proposed,which is theoretically shown to be effective to steer USVs towards the optimal formation.A numerical simulation example is provided to demonstrate the effectiveness of the proposed method.
Introduction: As effective tools for search, detection, navigation,rescue, and anti-terrorism attacks in sea areas, USVs are playing essential roles in maritime defense and security [1].Many countries have been making great efforts to the development of USV-related techniques, among which formation control is one of the core focuses.Aiming at steering USVs to achieve and maintain desired shapes, formation control of USVs has received considerable attention in the past two decades [2]–[4].For example, an USV formation control strategy under actuator saturation and unknown nonlinearities was developed [2].Moreover, fixed-time [3] and prescribed-time[4] issues were also addressed.By noticing that in practical situations, USVs may be involved in multiple tasks, e.g., when USVs are engaged in secure escort of an important ship, they may need to form a desired shape and avoid interceptions at the same time.Thus, optimal formation control, which allows USVs to solve the global optimization problem while maintaining the desired formation shape,may be beneficial to such cases [5].
Distributed optimal formation has received some attention in recent years.Based on a distributed optimization approach, time-varying optimal formation with quadratic global objective function was considered [6].Optimal formation with collision avoidance was addressed in [7] and predefined-time leaderless optimal formation was investigated in [8].However, these strategies are not designed for USVs.Inspired by the widespread applications of USVs, this letter focuses on the design of distributed optimal formation control strategies for USVs by using game theory.Though, a game-based formation strategy was studied in [9] for USVs, it is worth pointing out that the “optimal” issue was not considered and only a trade-off between formation and target tracking can be achieved.
Based on the above observations, the purpose of this letter is to construct a distributed optimal formation strategy for USVs, contributing to the community in the following aspects: 1) Different from [9], an optimal formation control problem for multiple USVs is presented, in which the USVs not only need to form a predefined shape but also solve a global optimization problem.A regularized game mapping is given for the formulated optimal formation problem, which is transferred to an optimal Nash equilibrium seeking problem.By leveraging techniques from regularization, the USVs are led to the “optimal direction”, which can hardly be achieved by existing results.2) A distributed Nash equilibrium seeking strategy is proposed to solve the optimal formation game for USVs.This strategy is constructed by a modular framework of a state regulator and a Nash equilibrium seeker, which is designed by regularized gradient search and consensus protocols.3) It is shown theoretically that the proposed seeking strategy is effective to achieve formation of USVs while solving the global optimization problem.
Problem statement: Consider a network ofNUSVs, whose dynamics are described by



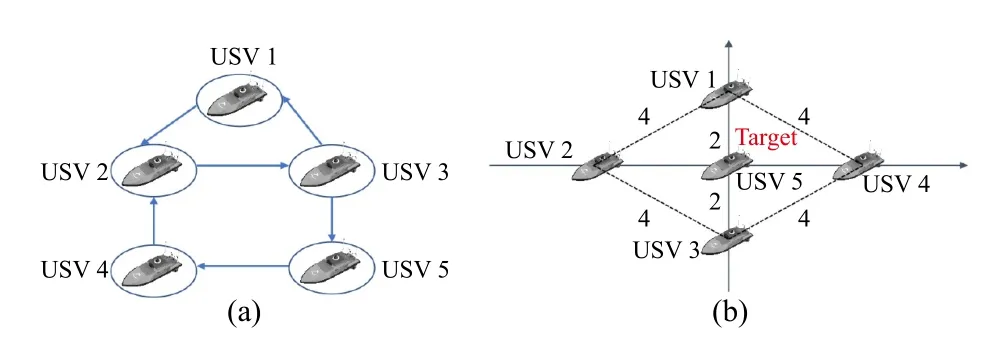
Fig.1.Communication graph and optimal formation in the simulation.(a) The communication graph for USVs; (b) Illustration of the optimal formation for USVs.


Fig.2.The position trajectories of USVs generated by (10).

Fig.3.The yaw angle trajectories of USVs generated by (10).
Conclusion: This letter has investigated an optimal formation control problem for multiple USVs.A game based formulation has been proposed for USVs to address this problem.Based on the formulated game, a modular framework consisting of a regulator and distributed Nash equilibrium seeker has been given to enable optimal formation for USVs.The effectiveness of the proposed method has been theoretically proven by using Lyapunov stability analysis.Future works will take collision avoidance, disturbances, and optimal formation of vehicular system (see, e.g., [16], [17]) into account.
Acknowledgments: This work was supported by the National Key R&D Program of China (2022ZD0119604), the National Natural Science Foundation of China (NSFC), (62222308, 62173181,62221004), the Natural Science Foundation of Jiangsu Province(BK20220139), and the Young Elite Scientists Sponsorship Program by CAST (2021QNRC001).
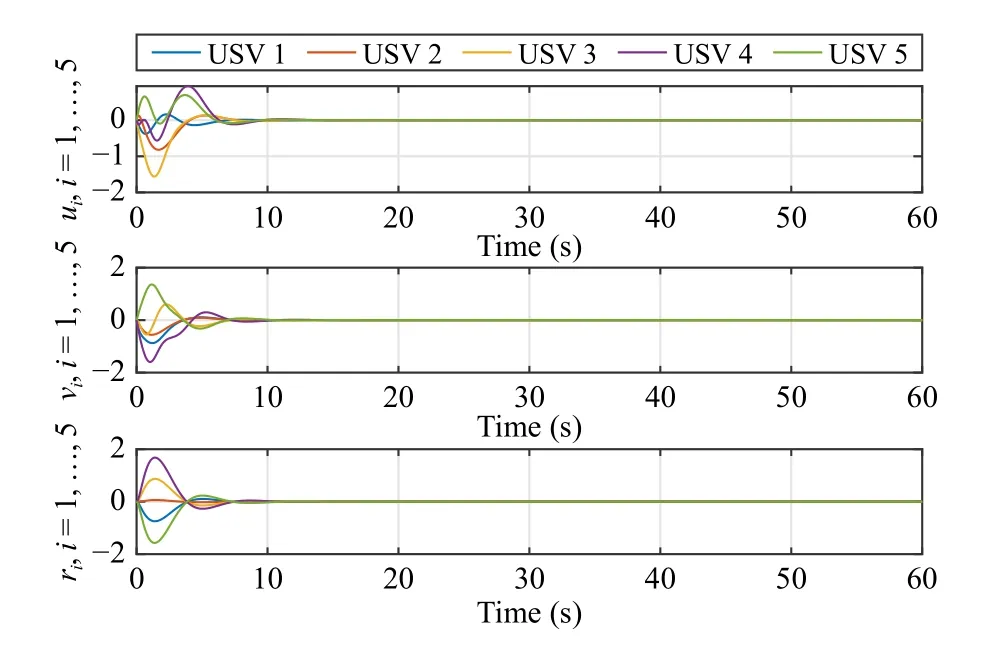
Fig.4.The surge, sway, and yaw velocity trajectories of USVs generated by(10).
 IEEE/CAA Journal of Automatica Sinica2024年1期
IEEE/CAA Journal of Automatica Sinica2024年1期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Sustainable Mining in the Era of Artificial Intelligence
- Fixed-Time Consensus-Based Nash Equilibrium Seeking
- Control of 2-D Semi-Markov Jump Systems: A View from Mode Generation Mechanism
- Autonomous Recommendation of Fault Detection Algorithms for Spacecraft
- An Incentive Mechanism for Federated Learning: A Continuous Zero-Determinant Strategy Approach
- Anomaly-Resistant Decentralized State Estimation Under Minimum Error Entropy With Fiducial Points for Wide-Area Power Systems
