Predicting impact strength of perforated targets using artificial neural networks trained on FEM-generated datasets
Nikita Kazarinov , Aleksandr Khvorov
a Saint Petersburg State University, Saint Petersburg 199034, Russia
b Higher School of Economics, Saint Petersburg 190121, Russia
Keywords:Machine learning Impact Dynamic fracture FEM Mesh distortion Optimization
ABSTRACT The paper considers application of artificial neural networks (ANNs) for fast numerical evaluation of a residual impactor velocity for a family of perforated PMMA (Polymethylmethacrylate) targets.The ANN models were trained using sets of numerical results on impact of PMMA plates obtained via dynamic FEM coupled with incubation time fracture criterion.The developed approach makes it possible to evaluate the impact strength of a particular target configuration without complicated FEM calculations which require considerable computational resources.Moreover,it is shown that the ANN models are able to predict results for the configurations which cannot be processed using the developed FEM routine due to numerical instabilities and errors: the trained neural network uses information from successful computations to obtain results for the problematic cases.A simple static problem of a perforated plate deformation is discussed prior to the impact problem and preferable ANN architectures are presented for both problems.Some insight into the perforation pattern optimization using a genetic algorithm coupled with the ANN is also made and optimized perforation patterns which theoretically enhance the target impact strength are constructed.
1.Introduction
Application of machine learning methods to engineering problems and to problems of mechanics in general has been intensively studied by a considerable number of research groups worldwide.Remarkable success has been achieved in coupling artificial neural networks(ANNs)with numerical methods used in hydrodynamics.Here works on application of deep reinforced learning for shape optimization and control can be mentioned[1,2].The ANNs are also used to rapidly obtain solutions of the fluid dynamics problems,which usually require considerable computational resources[3].
The ANNs are actively introduced into the solid mechanics field being especially effective for design of composites and prediction of their mechanical properties [4-6].The deep learning techniques for topology optimization problems are also actively studied [7]nowadays.Moreover, the machine learning based approaches are used for effective design of complex materials such as metamaterials and nanomaterials with unconventional peculiar mechanical properties [8,9].
In many of the above mentioned works the machine learning techniques are combined with classical numerical methods such as finite difference method or finite element method: the neural networks are trained using numerically obtained datasets and then are able to predict results for the yet unsolved problems.This approach seems to be especially promising for problems requiring huge computational resources and taking considerable time to solve.The material strength assessment under impact loading conditions is a typical representative of such problems, since transient processes should be accounted for, dynamic fracture models ought to be used and contact is usually involved.Here a number of works can be mentioned [10-13] including prediction and optimization of impact strength of laminates and using machine learning techniques to speed up dynamic FEM computations[14]-autoencoders trained on FEM-generated datasets are used to evaluate crashworthiness of tubes showing remarkable acceleration of the computations and high accuracy.In a number of works[15,16] the ANN models are shown to be effective for time series predictions in the impact tests, e.g.force-time dependencies obtained from simulations of dynamic fracture of rivetted tubes,honeycomb structures and crashing of tubes.One can also find applications of the ANNs trained on the FEM-generated datasets are already used to predict reliability of complex technological processes such as punch riveting[17].
The ANN models are also used for complex material characterization,such as assessment of JH-2 damage model[18]parameters based on the obtained experimental results [19].Moreover, the ANNs which were trained on experimental results can be used as material models describing complex material behavior under various loading rates and temperature conditions [20].The plasticity constitutive modelling using the ANN models is an exploding research field demonstrating high potential for managing both relatively standard cases [21] and complex situations and effects,such as fracture due to necking and yield drop phenomenon[22,23].
This way, the ANN models are now actively used for optimization properties (e.g.see application of the reinforcement learning techniques for the composite design [24]), acceleration of computations both by substitution of the direct computation with a trained neural network [14] and by implementing effective ANNbased material models which use either experimental or computational results as training data sets [25].Additionally, one can mention cases when ANN models trained on sets of experimental results are used to facilitate further experimental studies providing insights into possible outcomes of the experiments [26,27].
In this paper an ANN model is used to rapidly evaluate impact strength of PMMA plates with arbitrary perforation patterns (configurations).The ANN models are trained using the FEM-generated datasets and thus the ANN model is regarded as a fast alternative to a full FEM computation.We also propose a method to process computationally complicated cases when the FE mesh is considerably distorted in course of the FEM computation.Additionally,we consider the optimization problem using the trained ANN model as a faster alternative to the FEM computation in the genetic algorithm,which can be beneficial for the genetic algorithm tuning due to much shorter computational times.It is worth noticing that dynamic fracture of perforated specimens attracts attention of researchers, and cracks’ trajectories are usually the focus of the research [28-30].Moreover, interaction of a propagating crack with microcracks is also intensively studied [31].
The impact strength of the targets is characterized by residual velocity of the projectile after passing through the target: the higher is the residual projectile velocity the lower is the target impact strength.The trained ANN is able to predict the residual projectile velocity for the configurations which are not present in the training dataset and the strength estimations using the ANNs are instant compared to rather time-consuming FEM calculations.This can be beneficial for certain use cases (e.g.calculations using underpowered mobile devices or for web-based CAD/CAE applications where the result is expected to be obtained instantly and simultaneously by multiple users).Moreover, some plate perforation patterns appear to be problematic and cannot be processed using the developed FEM procedures due to extensive mesh distortion causing a prematurely terminated solution procedure.For such situations the ANN predictions can be useful as the result can be obtained without reducing the solution time step or any other FEM solver tuning.It is worth noticing that inconsistent element behavior is a common problem for the FEM-based impact simulations especially for high projectile velocities and complicated target shapes [32].
The paper is organized in the following way: firstly, the main impact problem and the auxiliary static plate deformation problem are formulated and stated.The section describing technical details of the FEM calculations and the architecture of the ANNs follows.The third section contains results for the both discussed problems and conclusions together with discussion are provided in the last section of the paper.
2.Statement of problems
The study objective can be formally stated in the following way:let's consider a family of M problems and each problem is characterized by a vector consisting of N parameters Pj=(Pj1,Pj2…,PjN),j?[1,M].Each problem(configuration)Pjis mapped to a result Rjusing FEM or any other numerical approach and situations when there is no result(Rj= ?) for a particular parameter configuration are not excluded (problematic cases).Thus, the data set (or the configuration family) can be encoded as
The goal is to construct an algorithm that would map some new unsolved configuration PM+1to a result RM+1without performing the full problem solution and would possibly process the Rj=?situations.The problematic Rj=?cases are supposed to be processed using data obtained from the normally solved problems.Vector Pjcan potentially describe the shape of the sample,material properties, loading or even mixture of them.In this study the Pjvector describes the perforation patterns and artificial neural networks are used as the predicting algorithm while the data set consisting of M solved problems is used to train the ANNs.The data set size M is considered as sufficient for the ANN efficiency to stabilize.
Two problems are considered in the paper:A very simple static plate deformation problem is discussed prior to the main impact problem in order to test the approach and to see how mechanical aspects of the problem can potentially influence the ANN model architecture and efficiency.For the plate deflection problem the solution is binary: the plate deflects either to left or right.The impact problem solution is a residual projectile velocity.
A two-dimensional formulation is used for the discussed problems, however axial symmetry is applied in the impact problem.The specimen models are composed of two types of square cells-a normal solid cell and a cell with a hole - a perforated cell.Combination of these cells yields the perforation configuration and thus random configurations can be generated forming a configuration set.The cell size can be varied and this way perforation patterns with different numbers of cells (perforation resolutions) can be obtained providing different configuration sets.Thus, in Eq.(1) N equals number of cells composing the sample and Piequals zero or unity describing a solid or a perforated cell, while M denotes the size of the data set needed for successful training of the ANN model.
The following issues and questions are to be covered for the problems:
? Sufficient size of the dataset for each configuration set which ensures high efficiency of the ANN model and therefore ability to rapidly obtain the problem solution without performing full FEM analysis.
? Suitable ANN architecture for the particular problem: balance between the architecture complexity,accuracy of the model and required data set size is sought for.
? Possibility to obtain the result for the configurations which cause failure of the FEM solver using the trained ANN models.
? Applicability of the developed ANN models as a fast FEM alternative for the optimization purposes and construction of optimized perforation patterns for higher impact resistance.
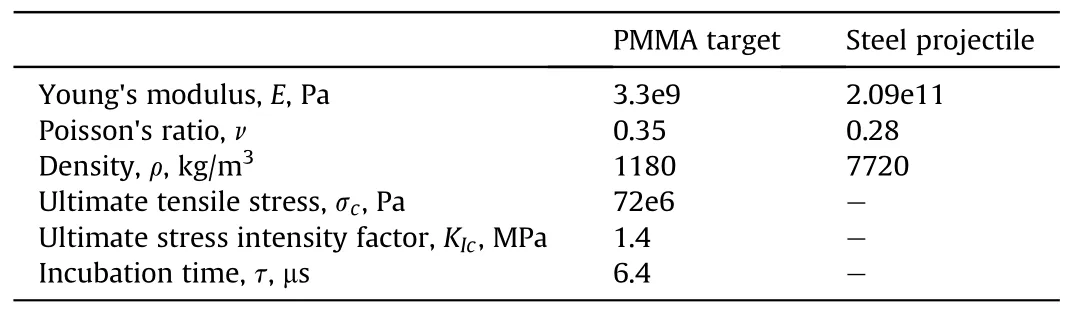
Table 1 Material properties used in the study.
For both problems the PMMA material is considered(properties are listed in Table 1) and the material behavior is supposed to be elastic.
2.1.Static deformation of a plate
A rectangular PMMA (properties listed in Table 1) plate with dimensions 20 mm × 51 mm is considered and plain strain formulation is applied.A 1 mm thick grip area is used and the perforated area is 20 mm×50 mm.The bottom edge of the plate is fixed and 60 MPa stretching stress is applied to the upper plate edge.Five configuration sets are studied: 2 cells by 5 cells (2 × 5 notation will be further used for the perforation resolutions),6 × 15,10 × 25,14 × 35 and 20 × 50.The load causes nonhomogeneous plate deformation and therefore deflection of the specimen to left or right depending on the perforation pattern.In this case the calculation result is the plate deflection side-left or right and the ANN is supposed to predict it for an arbitrary perforation configuration.
2.2.Impact problem
A 10 mm thick round PMMA plate with diameter 100 mm is hit by a cylindrical steel projectile (material properties are given in Table 1).The projectile has the following dimensions: diameter 6.3 mm and 500 mm height.The problem is solved in a twodimensional statement with axial symmetry applied meaning that the target and the projectile are both modelled as rectangles and perforation holes are in fact concentric canals inside the target.The target edge is fixed.
The projectile is slowed down due to interaction with the target and the calculation result is the residual projectile velocity.Obviously, the projectile deceleration depends on the perforation configuration, thus the ANN is supposed to predict the projectile's residual velocity for a given perforation pattern.
In this case three perforation resolutions and therefore three sets of configurations are studied:2 cells×12 cells(2×12),4×24 and 8 × 48, additionally, the plate is supposed to have a nonperforated layer for the contact stabilization - the sample plate models are shown in Fig.1.The base configuration model(with no perforation)is calibrated using experimental results on the PMMA plates impact.
The main studied projectile velocity is 95 m/s, however calculations with higher 199 m/s impact velocity are also performed to investigate the ANN model potential to predict results for the configurations with failed FEM calculations and thus no results.
3.Methods and techniques
3.1.Generation of datasets.FEM models
For both problems the configurations are assembled from preliminarily meshed cells - either solid or perforated.Such an approach leads to significant performance gains compared to a whole model meshing method.The configuration generation process is fully automated using Python scripts and ANSYS APDL scripting language.The perforation pattern is encoded using a rectangular matrix where zero stands for a solid cell and unity-for a perforated one.Details for each problem are given further.
3.1.1.Static problem
ANSYS FEM software is used to both generate the configurations and to obtain the solution.The meshed cells, a configuration example and a resulting deformation are shown in Fig.2.The bottom edge nodes are constrained in all directions.The plate deflection is measured using averaged horizontal displacements of the three nodes located on the upper edge of the plate.
3.1.2.Impact problem
In this case the target meshes are also assembled from solid and perforated cells using ANSYS APDL script.However,the problem is solved using LS-DYNA solver with an explicit time integration scheme.Thus, the LS-DYNA input is generated which is then modified in order to implement the custom dynamic fracture criterion.Square elements with four integration points are used to build the model.Here all the configurations are meshed with equally sized square elements as the element size is prescribed by the applied fracture model.The meshed cells, particular hole configuration and a resulting fracture pattern for a 95 m/s impact are shown in Fig.3.
It is known that the dynamic fracture of brittle solids is a complicated process and application of adequate fracture models is required in order to perform trustworthy simulations.The fracture models are supposed to be able to address specific dynamic fracture effects such as dependence of the material's strength on the loading rate (e.g.see Refs.[33,34]) or the fracture delay [35-37] phenomenon.Some widespread approaches to the dynamic fracture prediction are the stress intensity factor-based models for the dynamic crack propagation problems[38]and the models which include the strain rate explicitly with the JH-2[18]model being one of the most prominent and frequently used.In this work the fracture is predicted using the incubation time model [39,40] which has been proven to be effective for a range of cases including dynamic crack propagation [41,42] spallation [37], impact [43] and solid particle erosion [44] while being relatively simple.The fracture model description follows.

Fig.1.Representatives of the three configuration sets: (a) 2 cells × 12 cells; (b) 4 × 24; (c) 8 × 48.All the configurations have a nonperforated layer.
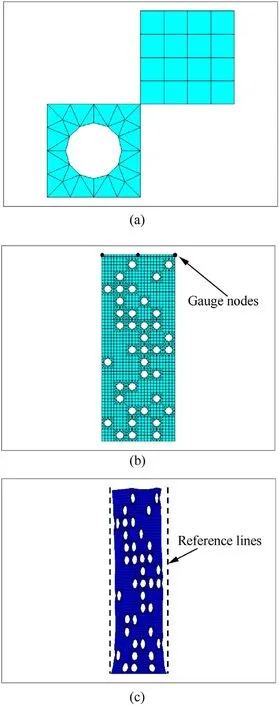
Fig.2.A particular 6 × 15 configuration for the static problem: (a) Meshed cells, (b)whole assembled mesh and a resulting plate deflection to the left as seen from comparison with the dashed vertical reference lines;in(c)15X scaling is used to show the plate deflection.
Consider a surface (a segment, since plane case is considered)located along the X axis between points x and x+ d with a timedependent normal stress σ(x,t) acting on this surface (Fig.5(a)).According to the incubation time model a cut along the surface will appear if the following inequality holds:
In Eq.(2)σcis ultimate stress of the studied material and d is a characteristic minimal size of the fractured zone, which sets the considered scale of fracture and thus damaged zones smaller than d are not regarded as fracture.The d parameter is calculated according to formula d = 2K2Ic/(πσ2c), where KIcis a critical stress intensity factor.This way, fracture is an essentially non-local process according to the used model and fracture at a single point cannot be considered.However, fracture at a set scale level is regarded as a result of preliminary fracture processes (e.g.coalescence of microdefects,microcracks and voids)which are accounted for through analysis of the stress history and a characteristic time parameter - the incubation time τ.The incubation time model relies on the impulse for the fracture prediction,since integration of stresses over area yields force and integration of force over time yields impulse.Eq.(2) is usually used to predict brittle fracture,however considerable success has been achieved in the dynamic plasticity modelling using the incubation time approach [45].

The developed two-dimensional model is calibrated in order to fit experimental results on the PMMA plates impact: the nonperforated base configuration model with 6.4 μs incubation time yield good matching with the experimental data (see Fig.5).
3.2.ANN models
3.2.1.Tested architectures of the ANN models
Generally speaking the artificial neural network is a complicated function that is capable of matching some set of data to a certain result.This function contains multiple parameters (weights and biases for the fully connected networks and filter parameters for the convolutional ones) which are adjusted to yield the best possible fit for the given data set and thus some trends and dependencies are established providing the possibility to predict the result with a certain level of accuracy.This parameter adjustment process is known as training.In the studied case the data set member is encoded with a matrix containing information about the specimen perforation: 1 stands for a perforated cell and 0 - for a solid one.The matrix components are the parameters Pjfrom Eq.(1) describing the particular problem.The results Rjare the plate deflection (to the left or to the right) and the projectile residual velocity depending on the problem.
Two types of the ANN models are investigated.Fully-connected models constitute the first class which also contains the very basic linear regression model.The studied problems resemble some known image processing problems (e.g.categorization of the depicted objects) and thus it is fair to suppose that the machine learning techniques used in this area can be applicable for the discussed mechanical problems.Thus,the second used model type is a convolutional neural network(CNN)[46].Models with different numbers of intermediate layers are tested.The 3×3 filter is used in the convolutional architecture(Fig.8(b)).
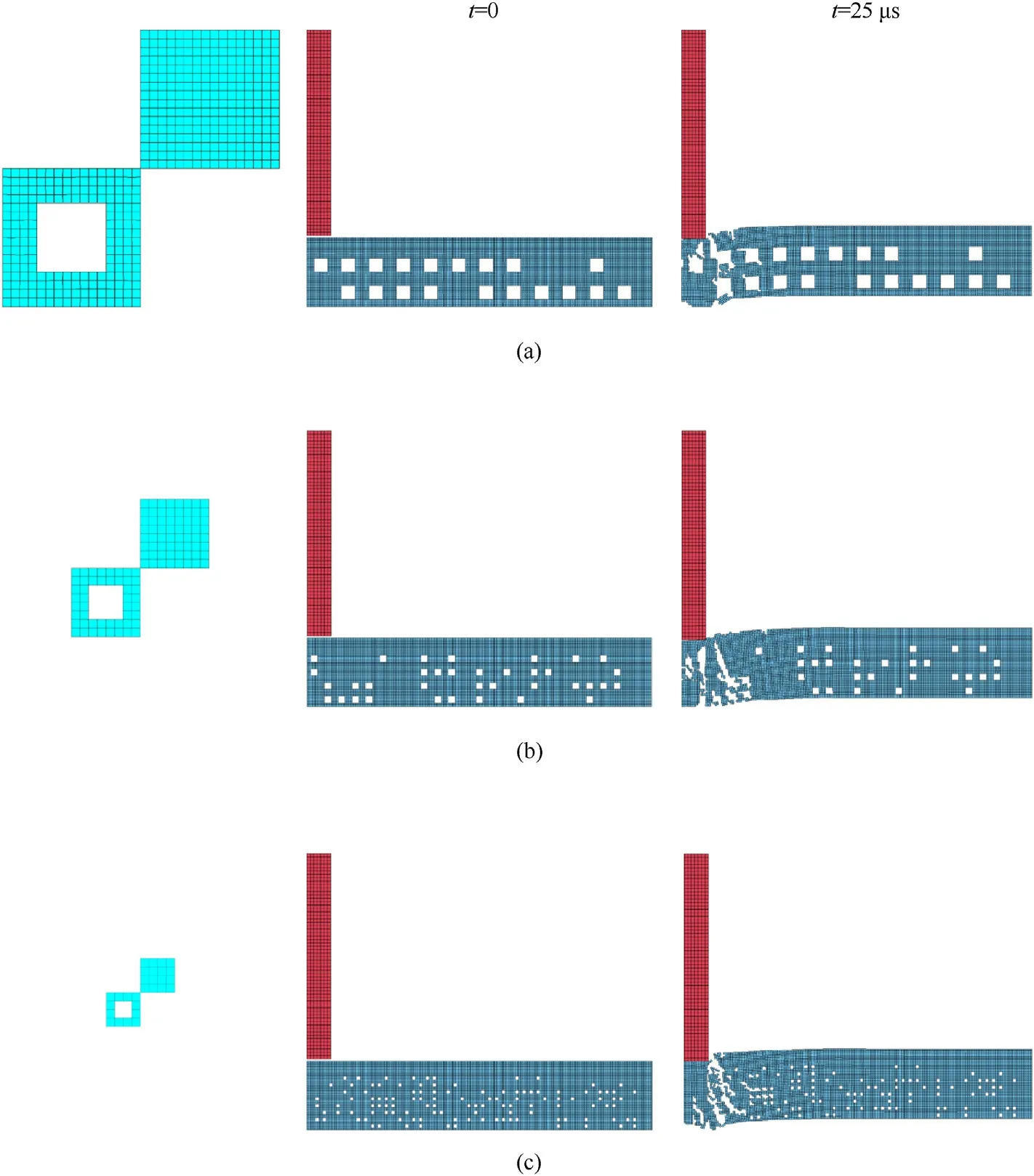
Fig.3.Cells, whole mesh and resulting fracture at time 25 μs for particular (a) 2 × 12, (b) 4 × 24 and (c) 8 × 48 configurations.
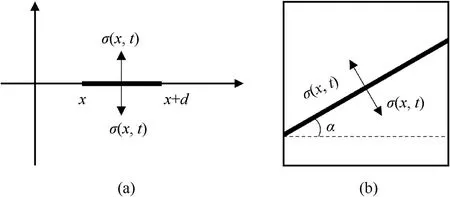
Fig.4.Interval of spatial integration in the incubation time fracture model (a) and element with a fracture area, where α = 0,π2,±π3,±π4,±π6.
For the fully connected ANN model the matrix describing the perforation pattern is converted into a single column: the matrix columns are stacked on top of each other and the resulting single column is then used as input for the fully-connected ANN.The convolutional neural networks operate with matrices without conversion.Further in the text the ANN models are denoted using the following notations: FC [n1,n2,…,nm] stands for a fullyconnected model with ni-sized m intermediate layers and FC [0]is a simple linear model, while CONV [n1,n2,…,nm] denotes convolutional ANN with M convolutional layers containing nifilters.In all cases ReLu activation was applied.For the CNNs 3 × 3 filters were used.ADAM algorithm was used for the parameter optimization.
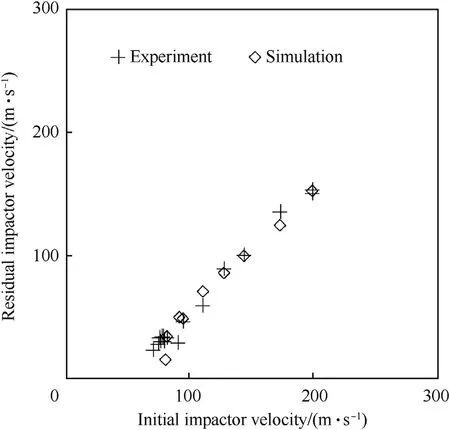
Fig.5.The FEM Model calibration-non-perforated base configuration;experimental results from Ref.[44].
Effectiveness and robustness of the two model architectures are investigated for both static problem and the impact problem.The model architecture selection is made based on the model's efficiency, simplicity (the simplest possible layer and filter design)and universality (high model efficiency for all configuration sets).All the models have been built using Python libraries Scikit-learn and PyTorch.
3.2.2.Evaluation of the ANN efficiency

Obviously R2 ranges from -∞to 1 and R2=1 indicates the highest possible efficiency of the model,while R2=0 corresponds to the baseline prediction.The accuracy metric is a ratio of number of correct predictions to total number of predictions.The 0.5-0.6 accuracy scores for the problems with balanced binary results sets(e.g.left or right;yes or no)are considered as poor since the model is essentially guessing.
The data sets are divided into train and test disjoint subsets.For the majority of studied problems, the test section has 1000 problems except for the perforation patterns with lowest resolutions(2 × 5 and 2 × 12 problems).
3.2.3.Optimization
As seen from the results some perforation patterns provide higher impact strength compared to a basic unperforated plate for the computations with 95 m/s projectile velocity.This provides an opportunity to perform some optimization procedures which use the trained neural networks and thus to test their ability to process rare cases.
In the studied case the configurations are denoted using matrices composed of discrete values-zeros and unities,since the cell can be either whole or perforated.Thus, the optimization methods based on the gradient descent[7]are inapplicable without complex restrictions and conditions since the optimization results will include matrices composed of float numbers from the [0,1]range.This way, heuristic optimization methods, such as genetic optimization algorithms [48], are preferable for this particular problem.
Shortly speaking the genetic algorithm is an enhanced version of a random search method.Instead of random generation of configurations which is used in the random search,a population of configurations is considered which evolves from stage to stage using crossbreeding and mutations.Each next population generation is produced using the best representatives of the previous generation due to the selection process.The trained neural network is used to quickly assess the configuration quality and to decide if its features should be kept for the further generations.The ANN models are used here as a fast alternative to FEM calculations which however results in an inevitable accuracy decrease.
4.Results
4.1.Static plate deflection problem
Fig.6 contains results on training of the ANN models developed for different configuration sets of the static problem.In all the graphs in Fig.6 the X axis is the number of configurations used to train the model and the Y axis is the model accuracy metric.The FC[0]model appeared to be the most effective for this particular static problem: while being the simplest one, it requires the smallest number of configurations for the model accuracy score to stabilize at the highest levels.Much more complicated models with higher numbers of intermediate layers are at most as efficient as the linear model requiring more data for training.Moreover, the convolutional models appear to be far less effective in this case failing to reach even 0.6 accuracy score for the higher resolution configuration sets.This probably should be expected as the plate deflection is controlled by how holes in the left and right halves of the plate are balanced.The convolutional neural network looks for certain local patterns which involve neighbor cells ignoring respective hole locations in the left and right plate halves.On the contrary, fully connected neural networks account for position of each cell and thus are able to analyze how holes and whole cells are balanced in the left and right plate halves.
Efficiency of the selected models applied to the different configuration sets with indicated dataset size are provided in Table 2.
To sum up, the following results were obtained for the static plate deflection problem:
? The ANN models provide high accuracy predictions as it is probably expected,since the observer is able to predict the plate deflection side for lower resolution perforation patterns(2×5,6 × 15) just looking at the perforation pattern.
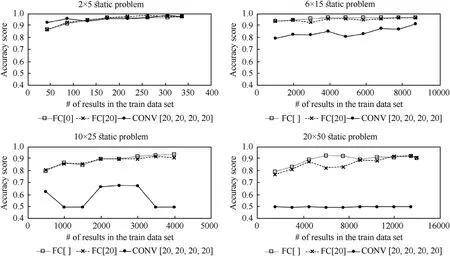
Fig.6.Dependence of the accuracy score of the ANN models built for static test problem and different perforation resolutions.
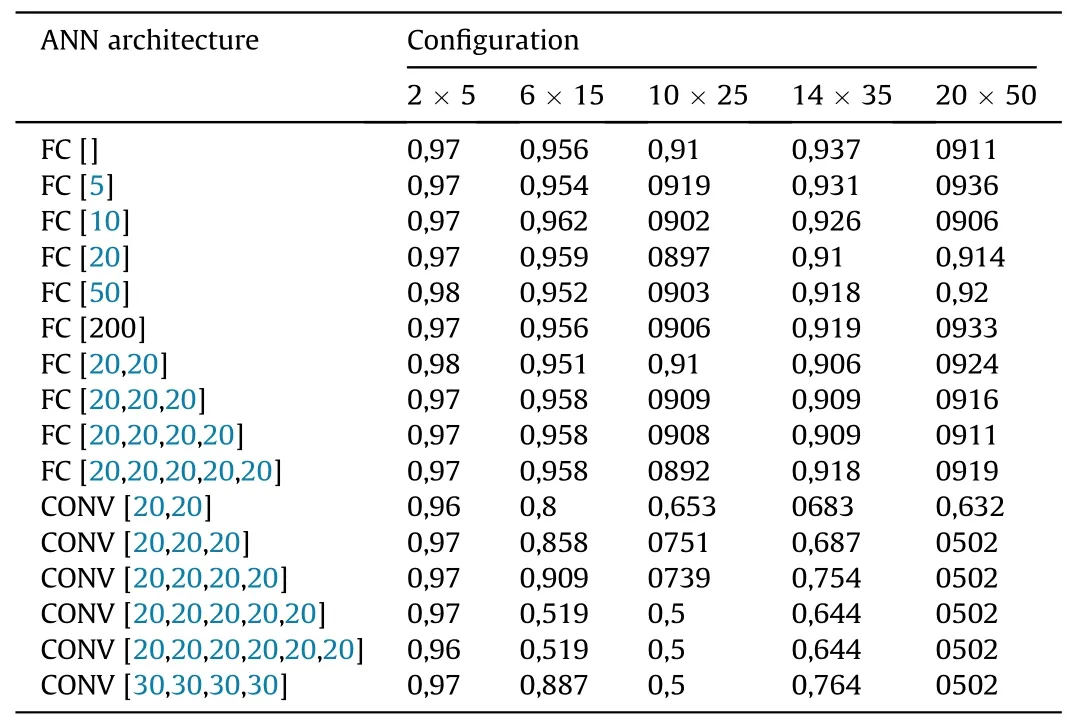
Table 2 Accuracy scores of different ANN architectures for the static plate deflection problem; the optimal one is highlighted.For all configurations the test data subset has 1000 problems except for the 2 × 5 case with 100 problems in the test subset.
? The simplest fully-connected model appears to be both accurate and easy to build and to train while the convolutional models fail to yield any accurate prediction despite the fact that the problem formulation is similar to the image processing problems - the model is supposed to distinguish the cell configurations.
4.2.Impact problem
4.2.1.Architectures of the ANN models,their efficiency and required sizes of datasets
For the impact problem a number of architectures of the neural networks are investigated.Table 3 contains information about performance of various architectures of the ANN models.In this case two models appear to be preferable in terms of accuracy,universality and required amount of train data: a fully-connected model with two intermediate layers (FC [20,20]) and a convolutional neural network with four layers - CONV [20,20,20,20].Information on training of these two models for the studied configuration sets is shown in Fig.7.
Fig.8 schematically shows two utilized types of the ANN models,while Fig.9 depicts diagrams with comparison of the ANN predictions with the FEM results.The dashed line in Fig.9 indicates the projectile residual velocity for a non-perforated plate and some configurations appear to slow down the projectile better than the basic non-perforated one.This formally means that for the case of a 95 m/s projectile some perforated configurations provide better protection than the solid one.This fact is used to test the developed optimization technique which is based on genetic algorithm and the trained neural network.The ANN manages to capture this effect,however the error for these cases is higher.Interestingly,there is no such effect for the higher 199 m/s projectile velocity case -results for all the configurations are equal to the base one at best and the ANN model prediction accuracy is better for this problem.This can be explained by the fact that the spread of results for the 199 m/s case is narrower comparing to other cases since for the higher projectile velocity the result is mainly defined by the number of holes under the contact area and not by their exact location-many configurations are indistinguishable from the ANN point of view resulting in equal residual projectile velocity and the problem complexity is reduced.
As expected the required data set size increases for problems with higher resolution of the perforation patterns and the increase is much more pronounced compared to the plate deflection problem.The 8 × 48 configuration appeared to be rather complex,requiring a lot of data to safely surpass the R2=0.9 efficiency level.
Predictions using the trained ANN models take considerably less time compared to the full FEM computation: fractions of a second compared to around 50 s (8-core processor).
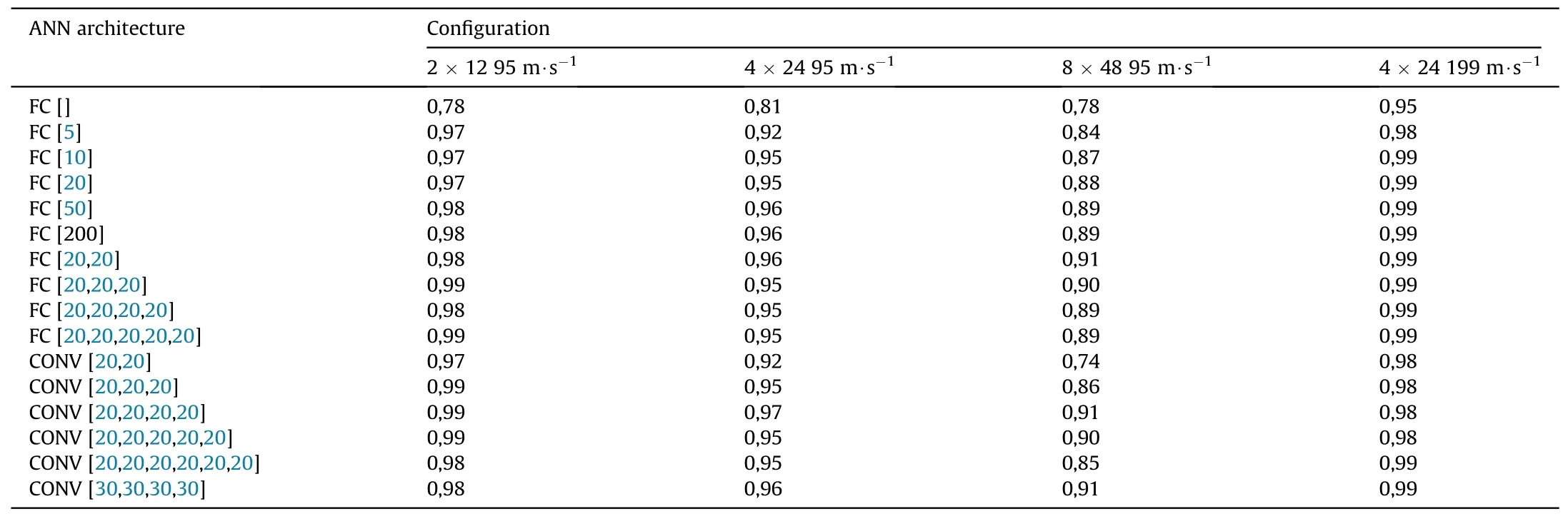
Table 3 Efficiency (R2 score) of various ANN architectures for different configurations of the impact problem.Projectile velocity is indicated for each problem.Optimal models are highlighted.For all configurations the test data subset has 1000 problems except for the 2 × 12 case with 500 problems in the test subset.
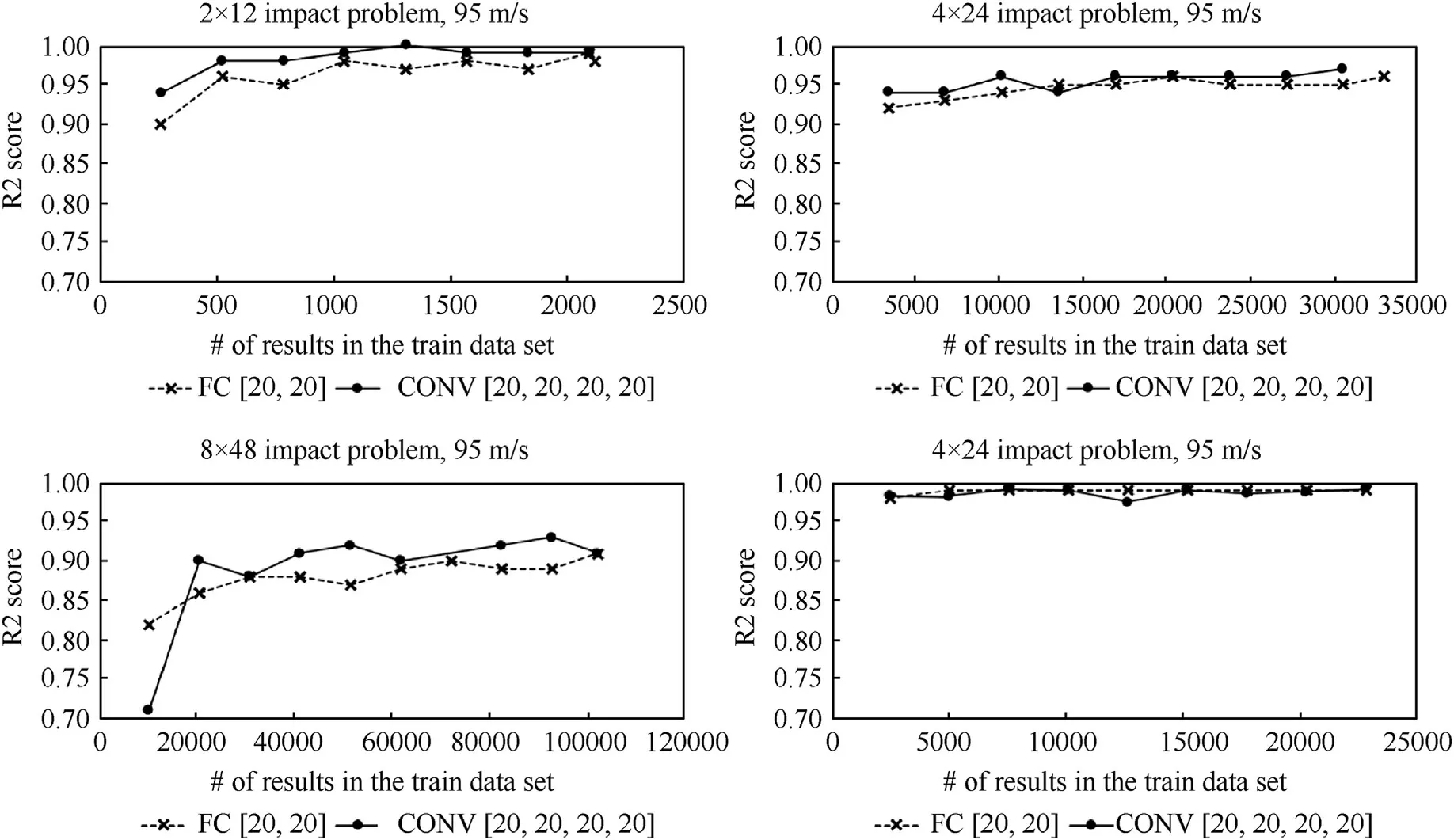
Fig.7.Efficiency (R2 score) of two types of neural networks depending on the dataset size for the impact problem.
4.2.2.Predicting results for problematic configurations
It is known that finite element meshes can be prone to considerable distortion when problems with high deformations are solved leading to errors and premature calculation stoppages[49-51].
General recommendations include reduction of a time step,mesh refinement,alternation of the contact parameters,changes of the material rheology[52],rezoning techniques[49,53]and simple deletion of heavily distorted elements which leads to fracture with no physical motivation.Alternative computational methods can be used to manage with highly deformed media such as Material Point Method, Smoothed Particle Hydrodynamics [54,55], Peridynamics[56] or coupling of different methods [57].
All the datasets for the impact problem contain configurations that resulted in an excessive element deformation causing the solver failure.For the 4 × 24 configuration set and a 95 m/s projectile velocity the solution could not be obtained for 199 configurations(out of 25 000).The problem is much more pronounced for the 199 m/s case: 7828 cases of premature computation termination due to error(out of 48 000).
The developed ANN models were tested for prediction of the computation success/failure for a particular configuration (4 × 24,199 m/s problem was used due to the considerable number of the failed computations).It is found that the developed ANN models are unable to predict the FEM computation failure yielding around 0.6 accuracy rate at most.It is a poor result from the predictions perspective, however this means that the configurations causing errors do not have any special features (combinations of the perforated cells)and thus do not form a distinguishable by the ANN class inside the whole dataset - calculation failure or success is almost random for the developed ANN model.This can serve as an indirect confirmation of the fact that the ANN models developed for the residual projectile velocity predictions can be applied to the failed configurations and as these configurations do not differ significantly from their processable counterparts.This way, the ANN model can be potentially extrapolated to the bad cases to bypass the FEM related difficulties and to predict the result for the cases when FEM computations either fail completely or require considerable tuning and modifications.Moreover, the predictions accuracy can be expected to be as high as in the normal cases.
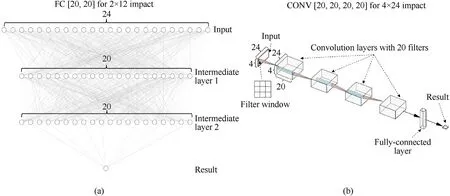
Fig.8.Schematic representation of the two utilized ANN architectures: (a) - the fully connected ANN (FC [20,20] for the 2 × 12 impact problem is shown); (b) - convolutional neural network with four convolutional layers with 20 filters each (CONV [20,20,20,20] and a final fully connected layer for categorization.
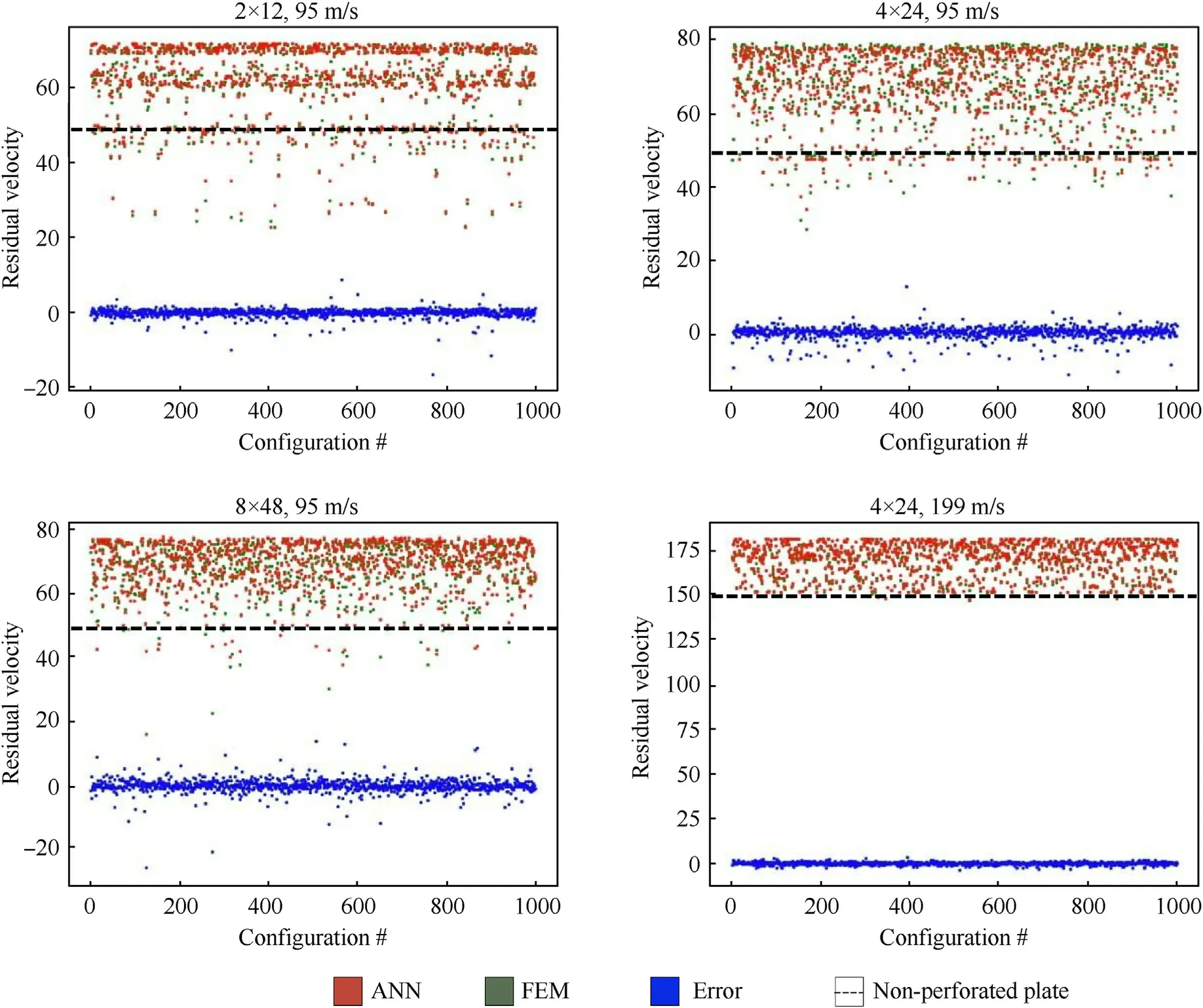
Fig.9.Accuracy of the ANN models developed for the impact problem, each dot indicates one problem from the test configuration set, dashed line indicates performance of the non-perforated target.
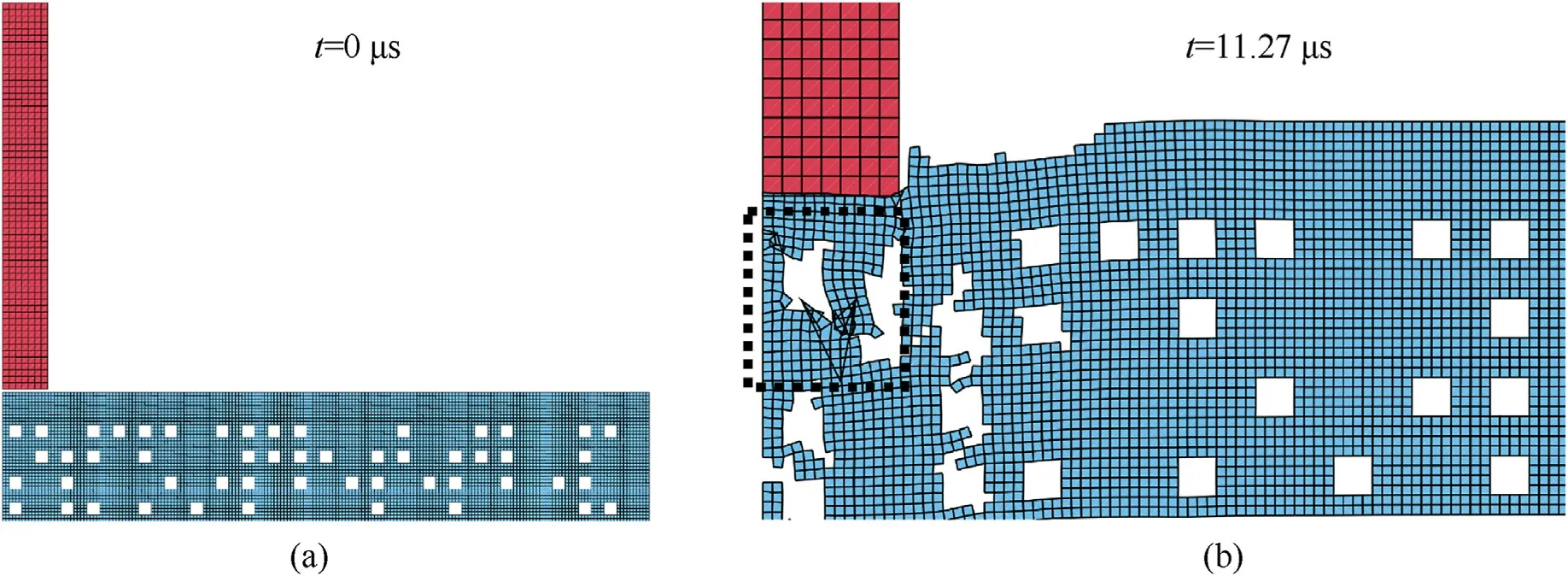
Fig.10.An example of (a) 4 × 24 configuration causing the computation failure and a zone with extensive element deformation (b) resulting in negative area error.
Some of the failed configurations were processed using FEM with a reduced time step(from 7.15e-8 s to 5.56e-8 s)leading to a normal termination of the computation.These results were used to evaluate efficiency of the ANN models applied to the problematic configurations and R2= 0.961 score was obtained for the 4 × 24 perforation pattern and 199 m/s projectile velocity.These figures indicate that the ANN models are applicable to configurations which are hard to process using the developed FEM scheme without tuning and adjustments.
An example of a problematic 4 × 24 configuration stroke at a 199 m/s velocity is shown in Fig.10(a)and (b)depicts a zone with inconsistent mesh behavior leading to an abrupt computation termination.This particular configuration could not be fixed by the time-step reduction and the ANN yields 151.2 m/s prediction for the residual projectile velocity.
4.2.3.Optimization results
The evolutionary optimization algorithm paired with the convolutional neural network (the СONV [20,20,20,20] architecture is applied) are used to construct some optimized 4 × 24 configurations for 95 m/s projectile velocity.For this problem the optimized configurations provide lower residual velocity of the projectile compared to the base model without perforation and thus theoretically better impact protection while being lighter.
One of the representatives of the family of the optimized configurations is shown in Fig.11.The optimized configuration behavior is compared to the plate without perforation.The holes make the spall related fracture more distributed leading to formation of two inclined cracks instead of a single vertical crack(dashed lines in Fig.11).The area beneath the impactor for the nonperforated plate is severely damaged losing its bearing capacity while the hole pattern results in a formation of a massive fragment which consumes momentum of the projectile and slows it down.
It should be noted here that this works for a relatively low 95 m/s velocity which is close to the threshold velocity.Successful application of the ANN model at a evaluation stage of a genetic algorithm proves that the ANN model is able to distinguish relatively rare and specific cases of the plate perforation.Moreover,application of the ANN at a evaluation stage of the optimizing algorithm can be of a great use for the algorithm tuning due to much faster performance.The genetic algorithm had a standard structure with mutation,crossover, evaluation and selection stages.
It is worth noticing, that other combinations of a heuristic optimization algorithms and an ANN are actively studied.In works[27,58-60]particle swarm and genetic algorithms are successfully used instead of conventional optimizers for the ANN parameter optimization.
5.Discussion
Artificial neural networks were found to be a powerful tool for reduction of computational costs for the particular problem of impact of perforated plates.The networks were trained using a preliminarily obtained set of FEM results and the number of required data is dependent on the perforation pattern resolution.On the one hand considerable computation resources are needed in order to obtain the dataset (for example, more than 100 000 problems should be solved for the 8×48 impact problem),on the other hand after the dataset has been obtained the solution of each next problem can be obtained instantly with high accuracy.Moreover, each next computation run does not require any FEM software which is often costly and requires licenses.Besides this the dataset generation is a completely automated procedure which is also beneficial for reduction of the development costs.This way, if the total number of problems to be solved exceeds the needed dataset size,the ANN based approach is worth considering.Such an approach might be useful for prototyping when general trends of the designed structure are of interest and many construction variants should be tested to obtain the desirable performance.Another possible use case is simultaneous solution of multiple problems,e.g.web-based CAD/CAE applications.It should be noted that realistic engineering problems would involve a complicated set of parameters to be varied which describe shape of the object, material properties and loading conditions or even a mixture of these parameters and each case should be studied separately.As it has been found even similar problems might require different architectures of the neural networks: while the convolutional neural network appeared to be successful for the impact problem, it was found to be inapplicable for the plate deflection problem due to purely mechanical reasons.
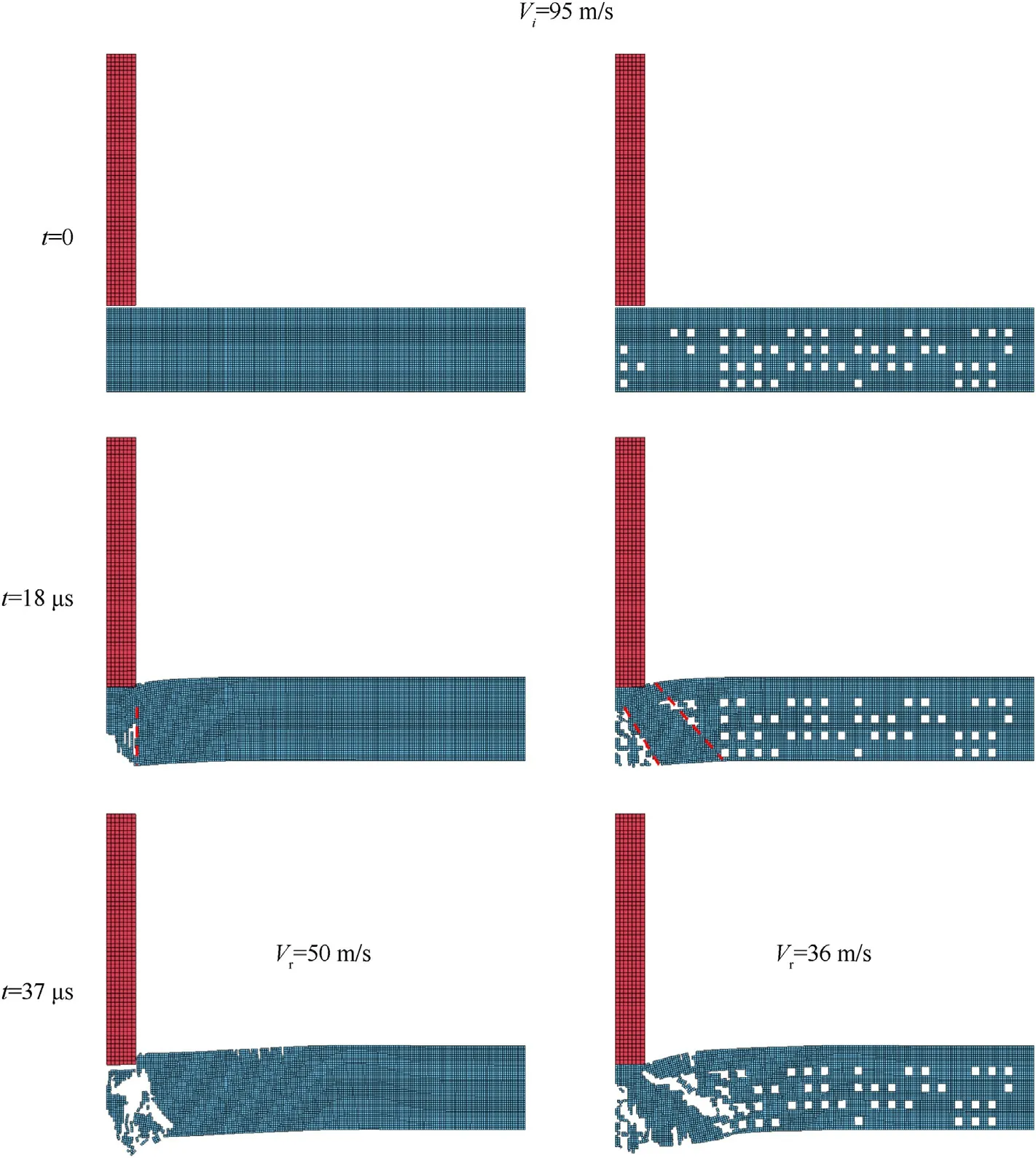
Fig.11.Comparison of performance of the non-perforated plate and of a plate generated by the optimization algorithm.Dashed lines indicate crack development paths.
The neural networks can be naturally used for the optimization purposes if algorithms based on gradient descent are applied.However,the studied case of the perforated plates is not suitable for these algorithms since the perforation configuration is encoded with binary matrices and the optimization procedure would yield matrices with real numbers from the[0,1]range.These values can be theoretically interpreted as the holes' diameters, but the resulting configuration would lie completely out of the main dataset which is characterized by discrete values.The gradient descent-based algorithms could be applied to the perforation problems if holes with arbitrary real diameters from a certain range were allowed.However,such modification would result in a much more complicated procedure of the dataset generation using FEM,since small holes would require very fine mesh and in general the procedure of assembling the sample using the pre-meshed cells would not be applicable.On the other hand, one could use cells with arbitrary material properties (e.g., Young's modulus or ultimate stress) instead of perforation which would allow non-binary optimization results, but it would be almost impossible to manufacture cells with given material properties and thus production of such samples seems unfeasible.
For the studied impact problem some optimized configurations were constructed using genetic algorithm which in fact does not require application of the neural networks.The developed ANN models were used at the evaluation stage of the optimization process being a fast alternative to the FEM calculations.The neural networks were used to quickly assess if a particular feature of the configuration (location of holes) is beneficial for the penetration resistance and thus should be kept for further generations of the configurations.Traditionally the evaluation stage would be performed using the full FEM calculation, but it would take considerably more time since one FEM run takes thousands of times longer than the ANN.It is also worth noting that GA-ANN combination(in sense that ANN is used at the evaluation stage instead of the full FEM calculation)can be used to examine the ANN model potential and accuracy.Moreover, this can be a fast way to tune the optimization algorithms since the time required for the evaluation can be significantly reduced if ANN is used instead of FEM:one GA run can be performed in a fraction of a minute instead of couple of days needed for the FEM-based GA.
The perforation configurations from the optimized set have the following common feature: two large angled cracks are formed instead of a single vertical crack in the base non-perforated sample.This leads to a formation of a relatively large fragment which takes in momentum from the projectile and slows it down.On the contrary in case of the non-perforated plate the fragment beneath the contact zone is eroded due to spallation.This way, for the 95 m/s projectile velocity some perforation patterns lead to better protection compared to the solid plate.However,for the higher 199 m/s impactor velocity this effect is not present.It is necessary to emphasize that this result should be regarded as a motivation for further research implying three-dimensional models and experimental tests if the effect takes place.
In addition to reduction of computational time and costs the developed approach can be used to overcome some known computational difficulties of FEM (or actually any other numerical method)applied to impact problems such as contact instabilities or inconsistent mesh behavior due to high strains.In the studied case some of the perforation patterns led to FEM failure however the information obtained from the rest of the dataset helped the neural network to predict the solution for the problematic cases too.The problematic configurations were found not to exhibit any specific features which could be distinguished by the neural network and thus they did not form a standalone subclass inside the dataset from the viewpoint of the neural network.This means that the developed ANN could be used to predict results for the problematic cases as they share features with the rest of the dataset.Consider a case when the computation fails for a particular combination of parameters Pj(Eq.(1))that characterize the problem(e.g.material model parameters or sample fixation and loading method or both,etc.)This problem can be potentially resolved using neural network model trained on a dataset consisting of problems with slightly altered Pjparameters (if alternation of Pjleads to successful FEM computations, of course).Inapplicability of the developed ANN model to prediction of FEM failure or success can be regarded as an indication that the ANN efficiency for the problematic configurations is comparable to the normal cases, since the problematic configurations do not form a subclass within the main dataset sharing features with the rest of the data and are not distinguished by the ANN model.It is worth noticing that high velocity of the projectile is a common cause of the FEM solution failure and the above described ANN based approach should not be expected to be very successful for the case.If the projectile velocity is included into the parameter array Pjand for all the projectile velocities higher than some critical value FEM fails, the problematic configurations clearly form a separate class.Thus, the train data would lack information about features of the problematic configurations which can possibly reduce the ANN model efficiency or make it completely inapplicable.This approach can be considered as deserving attention since such methodology can be possibly introduced in FEM routines to provide better user experience.
6.Conclusions
To sum up, the artificial neural networks can be regarded as a useful addition to the FEM(or any other computational method)for the cases when a representative of a family of similar problems is to be solved.The trained ANN models can help to obtain the result instantly and to overcome some possible computational difficulties encountered in the course of the FEM application.Moreover, the trained ANN models can be used for optimization purposes for example at the selection stage of genetic algorithms.
This has been shown to be true for a relatively simple case when the problem parameter array Pjcharacterizes the perforation pattern,however investigation of more complex cases(e.g.when Pjstands for a set of material properties or loading conditions)seems promising.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The work was supported by Russian Science Foundation [grant number 22-71-10019].
- Defence Technology的其它文章
- Mussel-inspired PTW@PDA composites for developing high-energy gun propellants with reduced erosion and enhanced mechanical strength
- An intelligent control method based on artificial neural network for numerical flight simulation of the basic finner projectile with pitching maneuver
- Shock Initiation Experiments with Modeling on a DNAN Based Melt-Cast Insensitive Explosive
- Coupling effect on the thermal hazard assessment of hazardous chemical materials via calorimetric technologies and simulation approaches
- Process and performance of DAAF microspheres prepared by continuous integration from synthesis to spherical coating based on microfluidic system
- TransTM: A device-free method based on time-streaming multiscale transformer for human activity recognition

