Free Energy of Anisotropic Strangeon Stars
Shichuan Chen, Yong Gao , Enping Zhou, and Renxin Xu
1 Department of Astronomy, School of Physics, Peking University, Beijing 100871, China; 2001110255@stu.pku.edu.cn,gaoyong.physics@pku.edu.cn, r.x.xu@pku.edu.cn
2 Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing 100871, China
3 Department of Astronomy, School of Physics, Huazhong University of Science and Technology, Wuhan 430074, China; ezhou@hust.edu.cn
Abstract Can pulsar-like compact objects release further huge free energy besides the kinematic energy of rotation?This is actually relevant to the equation of state of cold supra-nuclear matter, which is still under hot debate.Enormous energy is surely needed to understand various observations, such as γ-ray bursts, fast radio bursts and soft γ-ray repeaters.In this paper,the elastic/gravitational free energy of solid strangeon stars is revisited for strangeon stars,with two anisotropic models to calculate in general relativity.It is found that huge free energy(>1046 erg)could be released via starquakes, given an extremely small anisotropy ((pt-pr)/pr ~10-4,with pt/pr the tangential/radial pressure),implying that pulsar-like stars could have great potential of free energy release without extremely strong magnetic fields in the solid strangeon star model.
Key words: (stars:) pulsars: general – methods: numerical – (stars:) gamma-ray bursts: general
1.Introduction
A compact object composed of dense matter at supra-nuclear density forms after stopping the release of nuclear free energy in massive stars, which was initially termed as “gigantic nucleus” by Landau (1932).Can this kind of compact star release further huge free energy besides the rotational energy?This is an issue with a long history, relevant to the state equation of cold supra-nuclear matter,which is still challenging in both physics and astronomy nowadays(Xu 2023).
Observationally, an evolution of a post-burst relativistic fireball with free energy injection from the compact star through magnetic dipole radiation may provide a natural explanation for the plateau of γ-ray bursts (GRBs)(Dai &Lu 1998; Zhang & Mészáros 2001; Mei et al.2022).As the companion piece of GRBs,fast radio bursts(FRBs),especially the repeating ones with high burst rate, are calling for enormous free energy of compact central engines, which are most likely pulsar-like objects(Wang et al.2018, 2022; Luo et al.2020; Li et al.2021; Xu et al.2022).In addition,tremendous free energy is shown in the observations of the flares of galactic even extra-galactic sources, so-called soft γray repeaters, especially for the giant ones(Hurley et al.2005;CHIME/FRB Collaboration et al.2020; Fermi-LAT Collaboration et al.2021), with extremely bright giant flares with energy of 1044–47erg (Hurley et al.1999; Palmer et al.2005).
Theoretically,though the possibility of a solid core(Ruderman 1972; Canuto & Chitre 1973) cannot yet be ruled out, a conventional neutron star (NS) is fluid-like except for a solid crust(i.e., similar to a raw egg), the free energy of which could be negligible, but it might be significant in case of a state strongly magnetized(Duncan&Thompson 1992;Usov 1992;Thompson& Duncan 1993), so-called a magnetar(Thompson & Duncan 1995; Kouveliotou et al.1998) with extremely strong magnetic fields (~1013–15G).It seems that the theory of magnetars has been successful to explain many observations of anomalous X-ray pulsars and soft γ-ray repeaters, e.g., the energy budgets and the braking indices (Gao et al.2016, 2017; Wang et al.2020; Gao et al.2021).Nevertheless, nucleon-like units with strangeness, called strangeons, may form in bulk supra-nuclear matter produced during a core-collapse supernova, and a strangeon star (SS)(Xu 2003; Lai & Xu 2009; Lai et al.2023)should be in a globally solid state(i.e.,similar to a cooked egg)due to the large masses of and the strong coupling between strangeons.A calculation of the free energy for an anisotropic SS was presented in Newtonian gravity,showing a huge amount of energy released via starquakes when stellar stresses reach a critical value(Xu et al.2006), and an updated version with Einstein’s gravity will be given in the present work.
Although it is a common assumption in studying pulsar-like compact objects that the pressure is isotropic,it may not be true since some processes may induce anisotropy because of, for instance, a strong magnetic field (e.g., Cardall et al.2001;Frieben & Rezzolla 2012; Ciolfi & Rezzolla 2013; Gao et al.2015), relativistic nuclear interaction (Ruderman 1972;Canuto 1974), pion condensation (Sawyer 1972), phase transitions(Carter &Langlois 1998),superfluid core(Heiselberg &Hjorth-Jensen 2000),and so on.However,it is quite difficult to compute the exact anisotropic models on the physical ground from the first principle.Several heuristic anisotropic models have been put forward(e.g.,Bowers&Liang 1974;Herrera&Barreto 2013),based on some assumptions to make the models physically acceptable and available.
Additionally, the free energy of a pulsar-like compact object certainly depends on the equation of state (EOS) of bulk matter at supra-nuclear density, and it is generally thought that strangeness would play an important role in understanding the puzzling state, to be probably the first big problem solved in the era of gravitational-wave astronomy(Bodmer 1971; Witten 1984), see also Xu (2018)for a brief introduction.It is then suggested that pulsars could be strange quark stars (QSs), having similar mass and radius to that of normal NSs(Alcock et al.1986; Haensel et al.1986), which makes QSs a possible candidate model for this kind of compact objects.It is worth noting that the basic units of a strange star would be quarks for a QS, but could be strangeons if three-flavored quarks are localized in strangeons as for nucleons in the two-flavored case(Xu 2003).The model of an SS has been successful to explain many phenomena of pulsar-like stars, including the subpulse-drifting (Xu et al.1999;Lu et al.2019),the glitches interpreted with star-quakes(Zhou et al.2004, 2014; Lai et al.2018b; Wang et al.2021;Lu et al.2023), the Optical/UV excess in X-ray dim isolated NSs (Wang et al.2017), as well as massive pulsars (~2M⊙)proposed before discoveries(Lai & Xu 2009).Recently, the SS model is also consistent with the results of tidal deformability(Lai et al.2019) of and the light curve (Lai et al.2018a) from GW170817.In addition, the photon-driven mechanism might alleviate the current difficulty in corecollapse supernovae by forming a strange star inside the collapsing core(Chen et al.2007), producing more free energy injected into explosive shock waves than that of conventional neutrino-driven ones(Melson et al.2015).The model could also be tested in the future by detecting gravitational-wave echos associated with SSs (Zhang et al.2023).In summary, there are many differences between the SSs and normal NSs,not only in surface features,but also the global properties such as maximal mass and tidal deformability.It is expected to see these differences in future observations (see the review Lai & Xu 2017; Lai et al.2023 and references therein).
The free energy of solid SSs is focused on in the paper,with numerical calculations of the strain energy release during a starquake within general relativity in a spherically symmetric spacetime.This paper is motivated by Xu et al.(2006), which showed in Newtonian gravity that a solid pulsar can release a large amount of free energy from elastic or gravitational energy during a starquake due to the anisotropy of the solid star.We calculate here this kind of free energy with more physically acceptable anisotropic models and EOS in Einstein’s gravity.It is evident from our calculation that the huge free energy release of anisotropic solid SSs can naturally provide an alternative way to power γ-ray bursts, fast radio bursts, and soft γ-ray repeaters without extremely strong magnetic fields.Such kind of stress-energy stored in anisotropic stars to be releasable during a starquake has also been emphasized by Khunt et al.(2023), showing how the difference between sound propagation in radial and tangential directions would be used to identify potentially stable regions within a configuration.
Solid type stars have an advantage over fluid type ones(e.g.,conventional NS)in releasing the free energy from starquakes,since in the fluid-like star case, the starquake can only happen in the outer crust, while for the solid star, the whole star can release free energy by starquakes.This is one of the reasons we chose the model of SSs, one type of solid strange quark stars,rather than other fluid-like stars.Since we mainly focus on the difference in free energy of different parameters,we ignore the influence of anisotropy on the shape,structure,and radiation of the star.We think it is reasonable because the case we study has only small anisotropy ((pt-pr)/pr≤10-4, with pt/prthe tangential/radial pressure), which should have a minor influence on the results.We also neglect the influence of rotation of the star, since it has a tiny influence on the gravitational mass (hence the free energy) of SS in the case(Gao et al.2022).
The paper is arranged as follows.In Section 2, we will introduce the methods and models used to calculate the free energy of SSs in the anisotropic case, including the modified Tolman–Oppenheimer–Volkoff (TOV) equations in Section 2.1, two anisotropic models in Section 2.2, the EOS of SSs in Section 2.3,the method to calculate the free energy in Section 2.4 and the main results of our calculations in Section 2.5.We make conclusions and discussions in Section 3.We will use the cgs system of units throughout the paper.
2.Methods and Models
2.1.TOV Equations in the Anisotropic Case
For a spherically symmetric star modeled by perfect fluid in static equilibrium,the TOV equations constrain the structure of the star.But the isotropic star is only a common assumption.It is natural to believe that strongly interacting matter such as NSs should be described by locally anisotropic EOS (e.g.,Ruderman 1972; Bowers & Liang 1974).
For simplicity, consider a static distribution of anisotropic matter in spherically symmetric spacetime.In Schwarzschildlike coordinates, the metric can be written as:
The spherical symmetry spacetime also implies that the stressenergy tensor Tμνcan be written as (Dong et al.2023)
where ρ is the energy density,pris the radial pressure,ptis the tangential pressure, uμis the unit 4-velocity of the matter,uμ=gμνuν,and θμis the unit space-like vector in the direction of the radial vector, μμ=gμνθμ.
Combining with the Einstein equations,we have(Bowers&Liang 1974)
where Π=pt-prmeasures the local anisotropy and4π r2ρdris the mass within the radius r.
Equations (3)–(5) are the generalized TOV equations in the anisotropic case.Compared to the normal TOV equations,Equation (5) shows that the difference comes from the new variable Π=pt-pr, which should be determined by a new relation assumed, explained in Section 2.2.In this paper, we apply these equations to solid SSs.We think that it is reasonable since the SSs with small anisotropy can be approximated by anisotropic fluid.
2.2.Two Anisotropic Models
One of the most important issues is how to determine the model of Π, the difference between ptand pr.Since it is very difficult to obtain Π on physical grounds from the first principle, one could only guess some heuristic models.We assume the anisotropy is small so it does not change structures a lot, and the EOS only depends on prnot pt.
There are some minimal conditions on Π to make solutions physically acceptable (Estevez-Delgado & Estevez-Delgado 2018).In a nutshell, these conditions include: the interior solution should match continuously to the exterior Schwarzschild solution; the metric functions must be finite and non-zero within the star;the density and pressure must be non-negative and finite everywhere, and must be monotonic decreasing with radius; the radial and tangential pressure at the origin must be the same; the energy conditions should be satisfied; the causality condition must be satisfied within the star, i.e., the speed of sound must be lower than the light speed.
For simplicity, we choose two models of Π in our calculation.The first model is, where η1is a dimensionless constant,and R1is a constant with the dimension of length, to be R1=10 km for the typical radius of pulsars.The second one is the HB model with(Herrera&Barreto 2013), where η2is also a dimensionless constant.Theconstants η1and η2measure the anisotropy of the star,η1,2=0 implies that the star is isotropic and has no strain energy.Both models satisfy the conditions above and are physically acceptable.

Table 1 The Parameters of Lennard-Jones SS Model we used in the Calculation
2.3.Equation of State of Strangeon Matter
We choose the phenomenological Lennard-Jones model of SSs (Lai & Xu 2009), which assumes an interaction potential between two strangeons of
where ?is a constant that represents the depth of the potential,σ is a constant that represents the distance between two strangeons when their interaction potential u(r) is zero.
The Lennard-Jones model was usually used as the interaction between molecules, with the property of long-range attraction and short-range repulsion.The lattice QCD shows that there is a strong repulsive core of a few hundred MeVs at short distances (r ≤0.5 fm) surrounded by an attractive well at medium and long distances (Ishii et al.2007; Wilczek 2007).This kind of potential helps quark matter crystallize and form solid strange stars.
If we adopt the simple cubic lattice structure,and ignore the surface tension and vibration energy(since it is small compared to the potential energy and the rest energy), the total energy density ?qand pressure p of strangeon matter can be calculated as (Lai & Xu 2009)
where A12=6.2, A6=8.4, which are constants obtained from the simple cubic structure, Nqis the number of quarks in one strangeon,mqis the quark mass which assumed to be one-third of the nuclear mass and n is the number density of strangeons.
We adopt three groups of parameters of this Lennard-Jones SS model, which are named after their maximum gravitational mass.We choose the maximum gravitational mass Mmaxto be around 2.5, 3.0, 3.5 M⊙by setting different values of σ and ?.These parameters are listed in Table 1, wherens=(A62A12)12Nq3σ3is the surface number density of baryons, Nq, σ and ?are the same parameters as that in Equations(6)and(7).Nqis set to be 18,because a strangeon of 18-quark cluster has maximum symmetry, being completely asymmetric in spin,flavor,and color space(Michel 1988).The relation between the pressure P and energy density ρ for these three models is shown in Figure 1.The relation between the gravitational mass Mgand the radius R is shown in Figure 2,and the relation between Mgand the central energy density ρcis shown in Figure 3.The radius of SS with maximum mass in models LJ25,LJ30,LJ35 is 9.55 km,11.54 km,and 13.06 km,respectively.The adiabatic sound speed of SSs has been discussed in Lai&Xu(2009).This model of SSs is potentially stable against cracking0 (Abreu et al.2007; González et al.2015), which is satisfied almost everywhere within the star.
Though it has been reported that a black hole (BH) with a mass less then 3.5 M⊙was found (Thompson et al.2019), we think the model LJ35 is still meaningful.Since the 2σ confidence interval of the BH mass found in Thompson et al.(2019)is from 2.6 to 6.1 M⊙,it is still uncertain whether model LJ35 has exceeded minimum mass of BH or not.From the point of mathematics, it is acceptable even if 3.5 M⊙exceeds the upper limit of NS mass a bit,since we mainly focus on the influence of different parameters on the free energy.
2.4.To Calculate the Free Energy
With the generalized TOV Equations (3), (4), and (5) in the anisotropic case,Lennard-Jones SS EOS(7),(8)and the choice of anisotropic model, eitherwe have the complete equations to solve out the whole system.Once given the central energy density ρc,one can integrate the generalized TOV equations from the center to the surface, and obtain the radius, the gravitational mass Mgand the baryon mass Mbof the SS, which can be calculated as
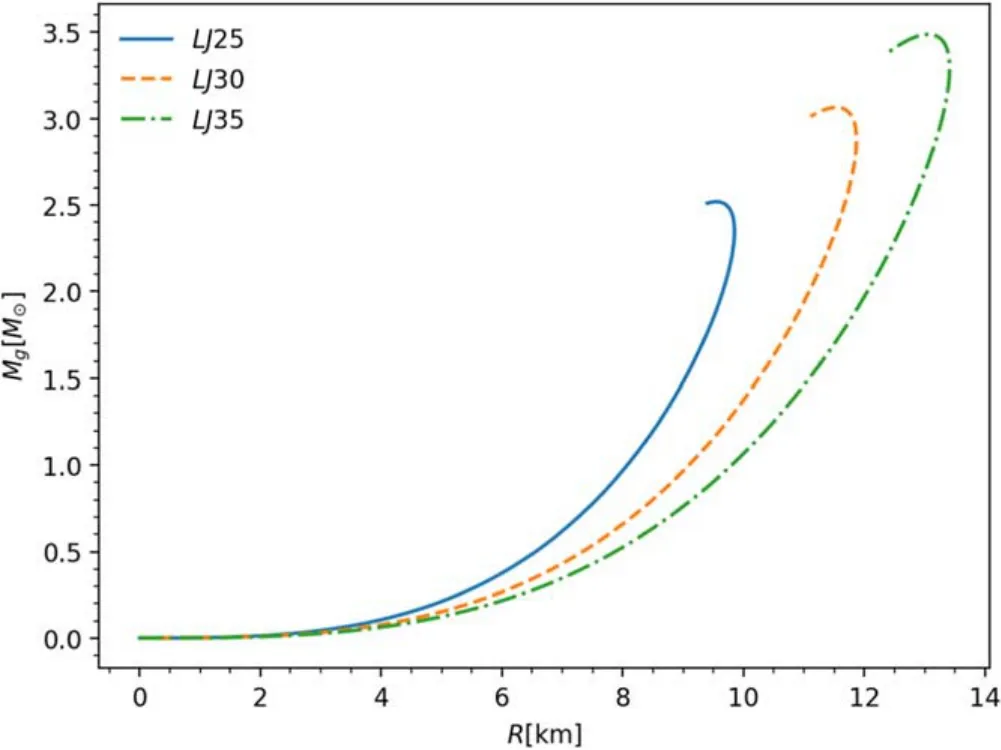
Figure 2.The M–R diagram of SS for different Lennard-Jones SS models adopted in the paper.
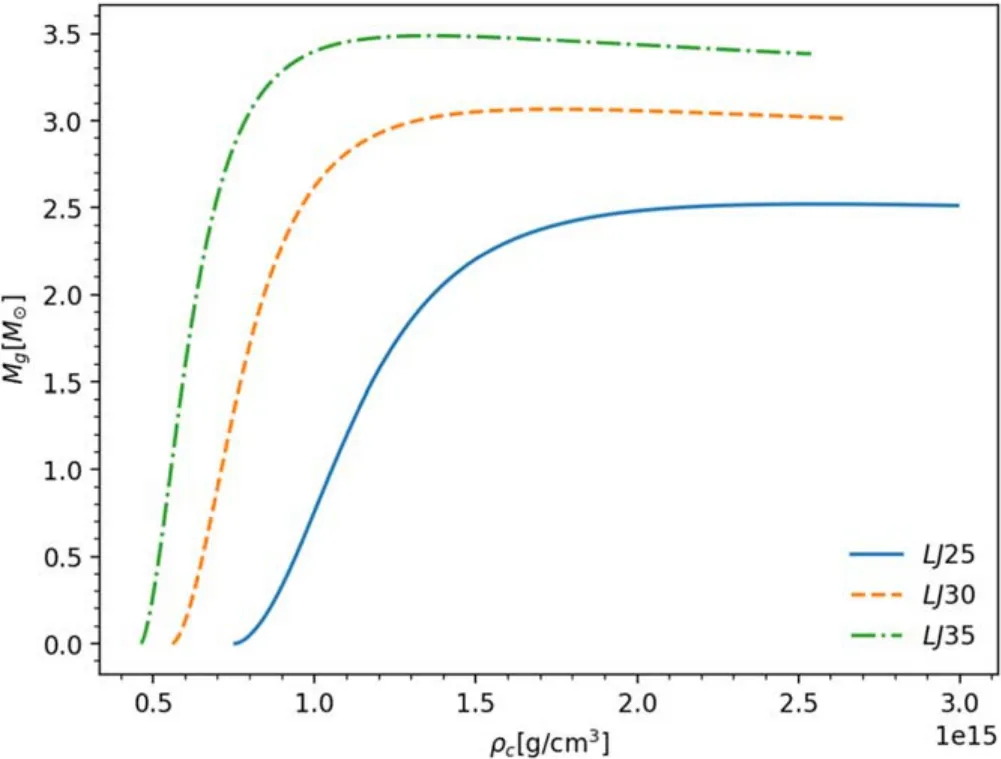
Figure 3.The M–ρc diagram of SS for different Lennard-Jones SS models adopted in the paper.
As the SS spins down, the centrifugal force will decrease,and elastic energy will accumulate to resist the deformation of the star.When the elastic energy exceeds a certain value, the star can no longer stand against it, and a starquake occurs.This kind of earthquake does not change the star’s volume.However, a solid star may have a starquake in case of accretion, which can change its volume.The two types of starquake models of SSs and their relation to glitches and pulsar’s spin down have been discussed in Zhou et al.(2014).
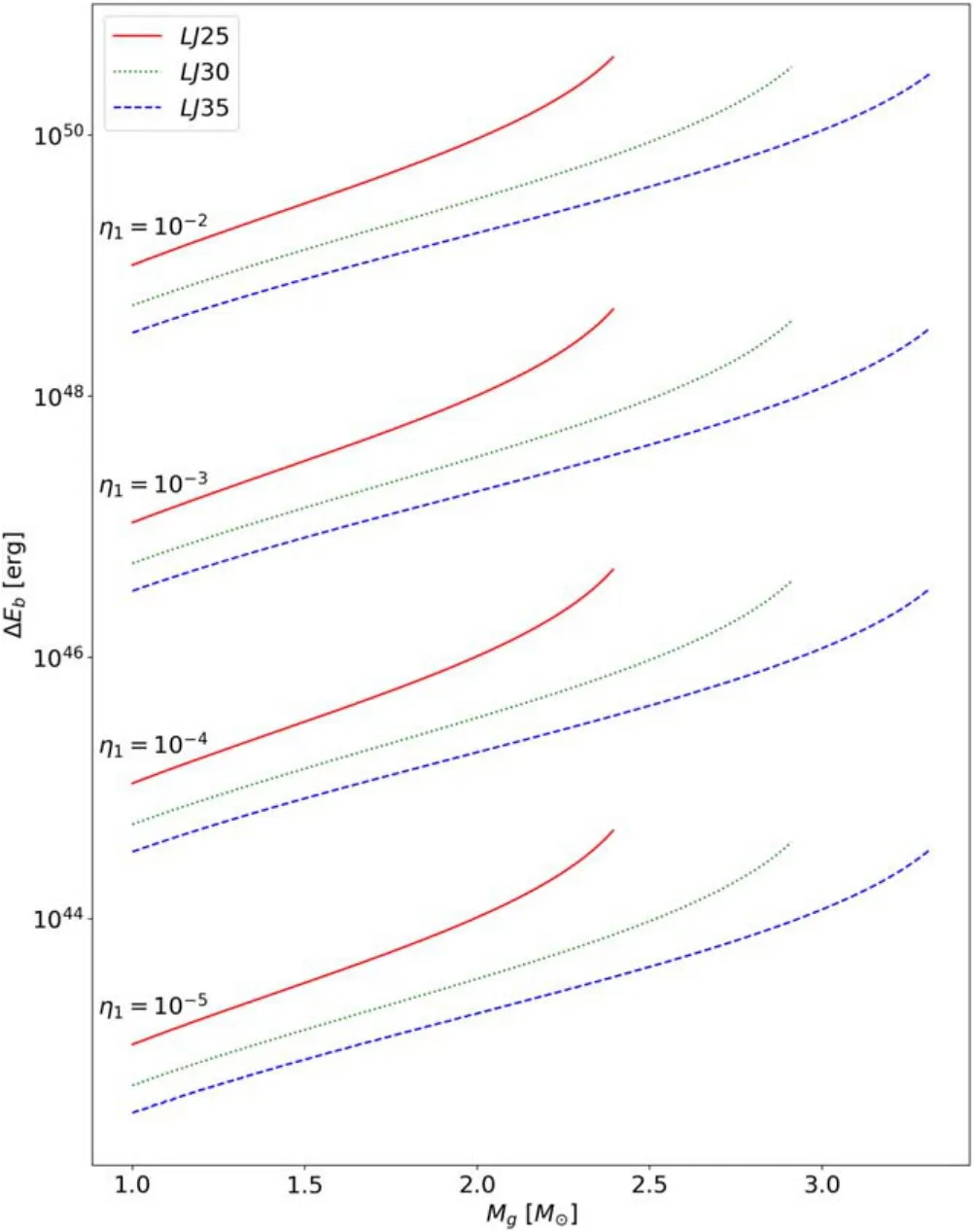
Figure 4.The difference of binding energy as a function of gravitational mass with the anisotropic model Π=-η1R1dpr/dr.Three different line styles (or colors) correspond to three choices of EOS, which are listed in Table 1.The lines in the same line style (or colors) from top to bottom have different η1,which are labeled in the graph.
The binding energy of the star can be calculated as Eb=(Mb-Mg)c2.Starquakes may cause the sudden change of Π, with a release of the gravitational energy as well as the strain energy.The difference of binding energy ΔEb=Eb(η1,2)-Eb(η1,2=0) between the star with η1,2≠0 and η1,2=0 may imply the free energy the star can release during the starquakes.
2.5.Results
The main results of our calculations are shown in Figures 4–7.Figures 4 and 5 show the difference of binding energy as a function of gravitational mass, implying the possible free energy the SSs may release via starquakes with different values of Mg, η1,2and different equations of states.Figures 6 and 7 show the value of Π/pras a function of radius, which measures the local anisotropy within the stars with different values of Mg, η1,2and different equations of states.

Figure 5.Same as Figure 4,except for the anisotropic model Π=-η2rdpr/dr.
From Figures 4 and 5, we can see that for larger mass and larger anisotropy (i.e., larger η), the potential free energy is larger.Given the same condition, LJ25 has the largest free energy,which means softer EOS tends to have larger potential free energy.Two anisotropic models have similar trends and shapes.
Figures 6 and 7 show that the higher the parameter η1,2is,the higher the Π is, implying that the dimensionless constant η1,2does represent the local anisotropy.It can be seen that anisotropy or the difference of pressure is close to zero near the center of the star,and grows higher with a larger radius.Three EOS models and two anisotropic models all have very similar trends and shapes.
From Figures 4 and 5, it is shown that for the modelwith η1=10-4–10-3or for the model Π=-η2rdpr/dr with η2=10-4–10-3, the difference of binding energy ΔEbis comparable to the typical energy of giant flare ~1044–47erg.From Figures 6 and 7,we can see that under these situations, the absolute value of the ratio of Π=pt-prto pris approximately 10-5–10-3.
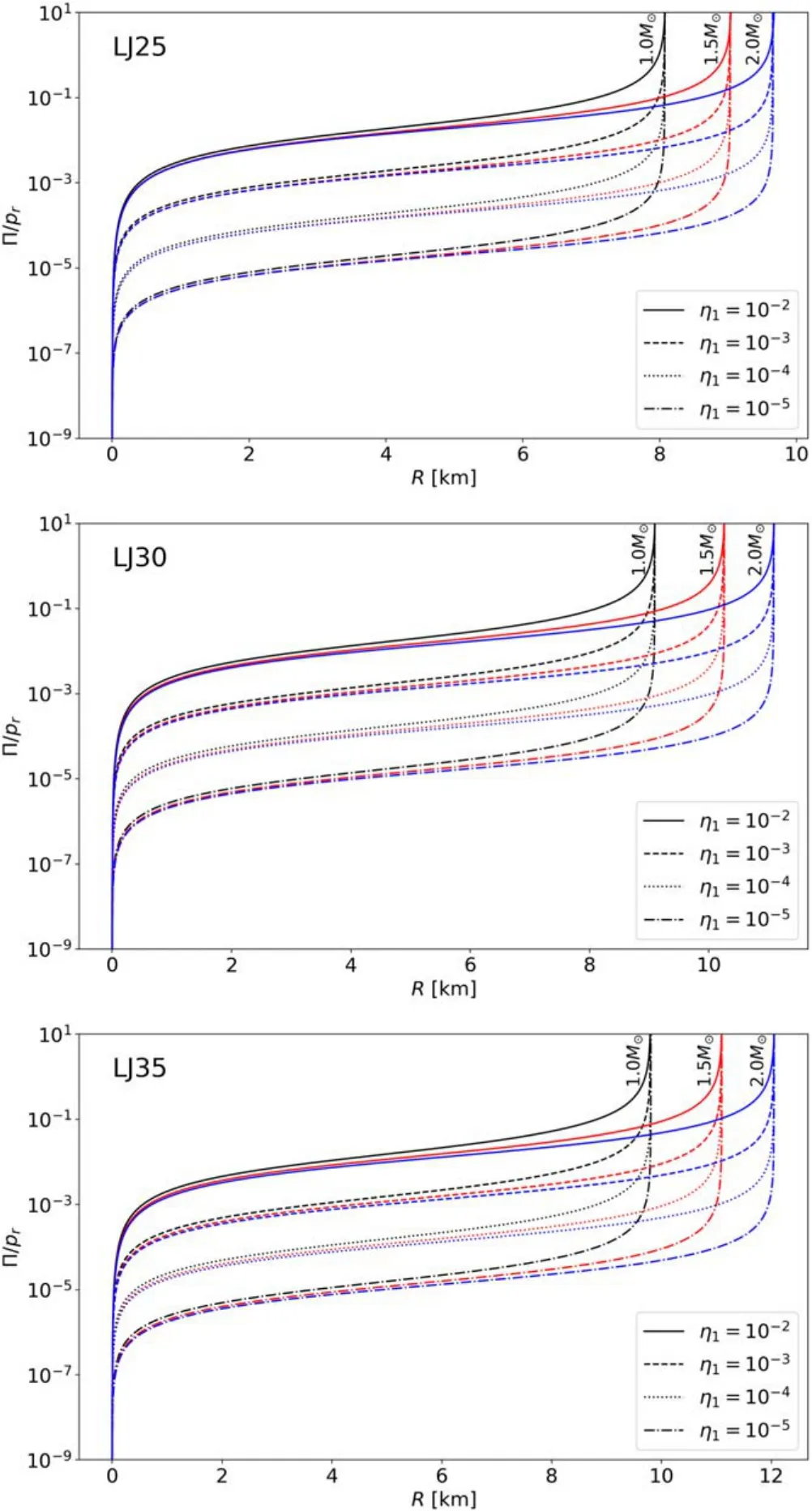
Figure 6.The value of Π/pr as a function of radius,with the anisotropic model Π=-η1R1dpr/dr.Three sub-graphs correspond to three choices of EOS listed in Table 1.Different line styles correspond to different values of η1.The lines in the same line style with different colors correspond to different gravitational masses Mg, which are labeled in the graph.
3.Discussions and Conclusions
The free energy of an SS would come from a release of the gravitational energy and the strain energy during starquakes,and extremely high magnetic fields might not be necessary in the case of SSs in order to understand various bursting events in astrophysics.The value of this free energy can be estimated as the difference of binding energy between the star with η ≠0 and η=0, where η is a constant that measures the strength of local anisotropy, and η=0 means the star is isotropic and has no strain energy.In this paper, we calculate this kind of free energy of SSs in general relativity,and find that a small degree of anisotropy(Π/pr~10-4)can account for a large amount of free energy, comparable to the typical energy of giant flares(~1044–47erg), as has already been illustrated in Newtonian gravity(Xu et al.2006).

Figure 7.Same as Figure 4,except for the anisotropic model Π=-η2rdpr/dr.
Since we cannot determine the anisotropic model on physical grounds from the first principle, we choose two heuristic models by guess in this paper, Π=-η1R1dpr/dr and Π=-η2rdpr/dr.Though we do not know the true form of the anisotropic model, these two toy models can at least show how anisotropy influence the free energy qualitatively.The influence of the anisotropy on the modified TOV equations is through Π=pt-pr,which only appears in Equation(5).So,if the values of Π within the star of two anisotropic models are similar,the value of free energy should also be close.Take the two models in the paper as an example.In the model Π=-η2rdpr/dr, there is a dimensionless constant η2which measures the intensity of anisotropy.In the model Π=-η1R1dpr/dr, we use the typical radius of pulsars R1=10 km to define a dimensionless constant η1.Since we have two dimensionless constants η1and η2which measure the anisotropy, we can compare them.From Figures 6 and 7, we can see that,when η1and η2have the same order of magnitude,Π/pralso have the same order of magnitude,and so is the value of the free energy ΔEb.For η1~10-3and η2~10-3, Π/pris around 10-4–10-3in the most part of the star except the center and the surface.Furthermore, as long as the anisotropic model can let Π/prbe over 10-4–10-3in the most part of the star,the free energy the star could release via starquakes can be over 1046erg, comparable to that of the giant flares.From Figures 4–7, we can roughly guess that the increase of an order of magnitude in Π/prcould make the free energy ΔEbincrease by two orders of magnitude.
However, it is still not clear how the potential free energy can be transformed into radiation via starquakes, so there are not many things we can say about the details of the energy release process.The starquakes may create a self-induction electric field (Lin et al.2015), which could initiate avalanches of pair creation in the magnetosphere and accelerate particles,inducing high-energy bursts (Thompson et al.2002; Xu et al.2006).Since the radiation is starquake induced, it should have some characteristics of quakes.Following the law of seismology, if small quakes happen frequently, no big quakes would happen, but a giant quake may occur after long-time silence.The glitches of pulsars may occur as X-ray transients,especially for the old SSs (Xu et al.2006).Since it is very difficult to get the anisotropic model on the physical ground from the first principle,we could only guess some heuristic toy models, which are required to satisfy some conditions to make sure the results are physically acceptable.All the factors that may have influence on the anisotropy, such as magnetic fields and relativistic nuclear interaction,are described roughly by the dimensionless constant η which represents the magnitude of local pressure anisotropy.We also ignore the impact of rotation,since it only has a minor influence on the gravitational mass,the change in Mgdue to rotation is less than one percent in normal cases(Gao et al.2022),which means that the rotation can be neglected when we focus on the free energy.
It is shown that the huge free energy (≥1046erg) could be released in an SS via starquakes, even with very small anisotropy(η ≤10-4).This kind of free energy may be related to γ-ray bursts, fast radio bursts, and soft γ-ray repeating sources, without the need of an extremely high magnetic field(~1015G).There are many improvements that can be made with this model in the future, since it is now only a phenomenological model with qualitative estimation of possible free energy in an anisotropic SS.More detailed models on starquakes and the process of energy transformation need to be built to give predictions on the observations, such as the spectrum of radiation or signals of gravitational waves.
Acknowledgments
The authors would like to thank those involved in the continuous discussions in the pulsar group at Peking University.This work is supported by the National SKA Program of China (2020SKA0120100).E.Z.is supported by NSFC grant No.12203017.
ORCID iDs
Yong Gao https://orcid.org/0000-0003-1390-5477
 Research in Astronomy and Astrophysics2024年2期
Research in Astronomy and Astrophysics2024年2期
- Research in Astronomy and Astrophysics的其它文章
- A Fermi-LAT Study of Globular Cluster Dynamical Evolution in the Milky Way: Millisecond Pulsars as the Probe
- Application of Regularization Methods in the Sky Map Reconstruction of the Tianlai Cylinder Pathfinder Array
- Effect of Cosmic Plasma on the Observation of Supernovae Ia
- Variable Stars in the 50BiN Open Cluster Survey.III.NGC 884
- Data-driven Simulations of Magnetic Field Evolution in Active Region 11429:Magneto-frictional Method Using PENCIL CODE
- The Clumpy Structure of Five Star-bursting Dwarf Galaxies in the MaNGA Survey
