COMPLETE K¨AHLER METRICS WITH POSITIVE HOLOMORPHIC SECTIONAL CURVATURES ON CERTAIN LINE BUNDLES (RELATED TO A COHOMOGENEITY ONE POINT OF VIEW ON A YAU CONJECTURE)*
(段曉曼) (關(guān)莊丹),2,
1. School of Mathematics and Statistics, Henan University, Kaifeng 475004, China
2. Department of Mathematics, The University of California at Riverside, Riverside, CA 92521, USA E-mail: xiaomanduanhenu@163.com; guan@henu.edu.cn
Abstract In this article, we study K¨ahler metrics on a certain line bundle over some compact K¨ahler manifolds to find complete K¨ahler metrics with positive holomorphic sectional(or bisectional) curvatures.Thus, we apply a strategy to a famous Yau conjecture with a co-homogeneity one geometry.
Key words K¨ahler Metrics; complete Riemannian metrics; open complex manifolds; holomorphic bisectional curvature; C* bundle; almost homogeneous manifolds
1 Introduction
A major component of the uniformization theory is to classify all complex manifoldsMnthat admit complete K¨ahler metrics with positive holomorphic bisectional (or just sectional)curvatures.WhenMnis compact, the so-called Frankel conjecture states that any compact K¨ahler manifoldMnwith a positive bisectional curvature must be bi-holomorphic toCPn.The closely related and slightly stronger conjecture of Hartshorne states that any projective manifold with an ample tangent bundle is bi-holomorphic toCPn.This Hartshorne conjecture was solved by Mori in his celebrated paper [22] in 1979.Around the same time, Siu-Yau [26]used differential geometric techniques to give a proof of the Frankel conjecture.
It is worth noting that the generalized version (namely, where ‘positive’ is replaced by‘nonnegative’, or ‘a(chǎn)mple’ replaced by ‘nef’) of Frankel’s conjecture was solved first by Mok and Zhong [24] for the Einstein case, then by Mok [20] for the general case in 1988, while the generalized version of the Hartshorne conjecture is still open.Important progress in this direction was made by Demailly-Peternell-Schneider [4] in 1994.
For when the manifold is non-compact, the following Conjecture was made by Yau in [30]:
Conjecture 1If an open and complete K¨ahler manifoldMnhas positive holomorphic bisectional curvatures, then it is bi-holomorphic toCn.
Related questions were first studied by Greene and Wu, and by Mok, Siu and Yau in the 70’s and 80’s; see [14-16, 21, 23, 25, 27, 28, 30, 31] and the references therein.
For an open and complete K¨ahler manifoldMnwith positive bisectional curvatures, it was shown by Greene and Wu [14] that the manifold is always Stein.
Note that whenn= 1, it is a classic result that any non-compact Riemann surface which admits a complete K¨ahler metric with positive curvature must be bi-holomorphic toC(in dimension 1, holomorphic bisectional curvature and holomorphic sectional curvature as well as the Riemannian sectional (that is, the Gauss) curvature mean the same thing).Thus this conjecture is a natural extension of the classical uniformization theory for Riemann surfaces to higher dimensions.
After the pioneering works mentioned above, Wu and Zheng, in [29], gave a classification of completeU(n) equivariant K¨ahler metrics onCnwith positive holomorphic bisectional curvatures.
We notice that if we blow up the origin ofCn,we obtain the line bundleO(-1)overCPn-1,and theU(n) action can be lifted toO(-1).Moreover, there is a power map
which is also aU(n) equivariant branched covering.Here,lis the holomorphic coordinate on the fiber, or the germ with regard toO(-k) as sheaves onCPn-1.
Furthermore, letωbe a K¨ahler metric onCnand letgbe a K¨ahler metric onCPn-1.We can lift bothωandgtoO(-1).We denote the lifted metrics byω0andg0, respectively, onO(-1).Thenωm=ω0+mg0is a K¨ahler metric for anym >0.In particular, ifωis aU(n)equivariant metric andgis the Fubini-Study metric, thenωmis aU(n) equivariant K¨ahler metric onO(-1).
Moreover, anyU(n) equivariant K¨ahler metric onO(-k) pushbacks to aU(n) equivariant Hermitian form onO(-1).
Therefore, combining the methods in [29] and [7], we can try to construct K¨ahler metrics with positive holomorphic bisectional curvatures onO(-k).
In every K¨ahler class of a compact almost homogeneous manifold with two ends, we found an unique Calabi extremal metric in [6, 7], Moreover, we found an unique extremal metric in a given K¨ahler class on a certainCP1bundle if the function Φ there is positive.We realized in[10] that this is equivalent to the geodesic stability of the K¨ahler class.
In [11], we proved that for these kinds of manifolds, there is another natural K¨ahler metric in the given K¨ahler class.
DefinitionFor any given K¨ahler class, an Hermitian metrichis a Maxwell-Einstein metric conformally related to the K¨ahler class ifh=u-2gis a Riemannian metric with a constant scalar curvature such thatuis the Hamiltonian function of a holomorphic vector field related to a K¨ahler metricgin the given K¨ahler class.
Proposition 1([11]) For any K¨ahler class on a compact almost homogeneous manifold with two ends, there is at least one Maxwell-Einstein metrics in the given K¨ahler class.
In this paper,we deal with open K¨ahler manifolds.Similarly,we could regard all the K¨ahler metrics onO(-k) as being with a form ofωmas in the K¨ahler classKm.HereKmis just the K¨ahler class onO(-k) with its cohomology class determined bymg0onCPn-1.O(-1) has a common open set withCn,On=Cn-{0}.Similarly, forO(-k) withk >1, there is an open set withOnas a finite covering which isU(n) equivariant.
As in [29],ω=?p, withpbeing a function ofr=‖z‖2onCn, and therefore onOn.
We notice thatGL(n,C) is also raised toO(-1) and comes down toO(-k).Therefore,GL(n,C) has an open orbitOnonO(-1), andO(-k) is almost homogeneous.Also,U(n) hasS2n-1orbits inOn, as real hypersurfaces.Therefore,O(-k) is a co-homogeneity one manifold.We denote the open orbit byOnk.
On the other hand, we notice that
for a special functionp0ofr.In particular, we always have thatgm=?pmfor some functionpmofronOnk.Therefore, all the calculations of [29] go through, at least onOnk.
Compared with [7], we have the following:
Main TheoremFor any K¨ahler classKmon an open almost homogeneous manifoldO(-k)of complex dimensionn, there are many(no)U(n)equivariant complete K¨ahler metrics with positive holomorphic (bisectional) curvature in the given K¨ahler class.
We notice that whenn= 2,O(-2) is just the canonical line bundle and the cotangent bundle overCP1, so we expect that the positive rational multiple canonical line bundles and the cotangent bundle over a compact K¨ahler manifold with positive holomorphic sectional curvatures always have a complete K¨ahler metric with positive holomorphic sectional curvatures.
On the other hand, an easy argument from [7] shows thatO(k) withk >0 does not admit a complete co-homogeneity one K¨ahler metric with positive holomorphic sectional curvatures.Therefore, we expect that the positive rational multiple anti-canonical line bundles and the tangent bundle of a compact K¨ahler manifold does not admit any complete K¨ahler metric with positive holomorphic sectional curvatures.
In the next section, we shall give some detailed calculations of the curvature tensors which do not seem to be available in the literature.Section 3 deals with the examples onO(-1);here, Theorem 3.3.1 is one of the cruxes of this paper, while Theorem 3.2.1 eventually leads to the solution for the line bundlesO(-k) with Theorem 3′from the next section.In Section 4, we achieve the goal of this paper onO(-k) fork >1.Further results have been also obtained in cooperation with the second author and his PhD.student M.X.Liang [12] on the examples of positive holomorphic sectional curvatures onO(-k) with a functionφ(U) without an asymptote or with a horizontal asymptote.Therefore,Theorem 3′and 3′′in the next section can be regarded as other cruxes of this paper.
To answer one of the questions on the Ricci curvature for these examples, we also notice in Remark 3.1.1 that the Ricci curvature is, in general, not necessarily positive.However, this is not our primary interest, so we will just leave things there.
To end this introduction, we would like to mention that there has been some critical new progress in the direction of Yau’s conjecture after [29], including but not limited to [3] and[18].This has been our motivation in this work, with a co-homogeneity one approach without knowing [31] from the start.
This article also serves as an exposition of both [29] and [7], as well as [11].Therefore, we will copy some of the material from them as we need, in this paper.Our Theorems 3.1.1, 3.2.1 were obtained in the summer of 2020.The second author gave a series of talks on them at Henan University around that time.Most of the rest of the results were obtained in the spring semester of 2021, and were parts of the master’s thesis of the first author [5].Our examples in Theorems 3.1.1 and 3.2.1 have a better smoothness than example 3.25 in [32] onO(-1), and they have a different flavor (that was what the second author told Professor Yang in December 2020, without knowing their earlier example 3.25 in [32]).In a talk in March 2022, Professor Bo Yang mentioned that, with Professor Zheng, he obtained many more examples at the end of 2021, though seems that they used a mildly different method; see [33].
2 Calculations of The Curvature Functions

Next, let us compute the curvature tensor ofω(h).Following Klembeck [17], let us fix a pointx= (z1,0,···,0).Klembeck ([17]) computed the components of the curvature tensor atxunder the coordinatezas

The above setting is almost exactly the same as that in[29],but for our future calculations,let us present it again here.


We also can see that all other curvatures, other than those that can be obtained by the standard curvature symmetries, are zeros.
If we have positive holomorphic bisectional curvatures,thenA,B,Cas special holomorphic bisectional curvatures, are positive.On the other hand, ifA >0,B >0 andC >0, by the symmetries, we only need to check that the holomorphic bisectional curvatures are positive atp.
We can assume thatX=x1e1+x2e2and thatY=y1e1+y2e2+y3e3.Here, we choose the corresponding orthonormal basis instead of the natural basis.
We have that
and =0 only ifx1y1=x1y3=x2y2=x2y3=0.However, we then have thaty3=0 and that
Therefore,the holomorphic bisectional curvature is always positive.We notice that there was a mistake in [17] regarding the choice of the two vectorsXandY, and that there was a mistake in [29] regarding the formula of the holomorphic bisectional curvature.
If one writes the metrics as in [7], we can restrict ourselves on the complex line passing through (1,0,···,0).For convenience, we denote the complex variable byz=x+iy, which is not to be confused with the earlier notation.Then we get that


An easy consequence of Lemma 1 is the following corollary:
Corollary 1OnCn,ω(h)has a positive(nonnegative)holomorphic bisectional sectional curvature if and only ifφis concave (semi-concave) down with respect toU; that is,φUU <0 (≤0), and (2.2) holds.Moreover, we have in this case that, 0<(≤)2B,C <(≤)U-1.In the second case, ifB(U0)=0 orC(U0)=0 at some pointU0, thenφ(U)=2UforU ≤U0.
ProofBy [29],ω(h) has a positive holomorphic bisectional curvature if and only ifA >0,B >0 andC >0.
By Lemma 1,A >0 is the same asφUU <0.OnCn,
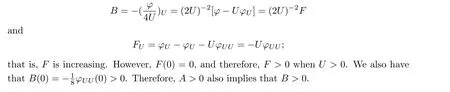
Moreover, we see that in this case,F <φ <2U.Therefore, 0<B <(2U)-1.Things are similar for the equality case.IfB(U0)=0, then
This implies thatφis just the tangent line of itself atU0,and thatφU=φU(0)=2 forU ≤U0.
Now letG= 2U+m-φandGU= 2-φU.ByGUU=-φUU >0 andGU(0) = 0,we get thatGU >0 whenU >0.Therefore, byG(0) =m= 0, whenm= 0, we see thatG >0 whenU >0.Also,C(0) = 2m-1>0 whenm >0.Whenm= 0, we have thatC(0) =-4-1φUU(0)>0; that is, ifA >0,C >0 also.Obviously, we haveUC <1.IfC(U0)=0, thenφ(U0)=2U0, andφis just 2UforU ≤U0.
We have thus proven the corollary.□
Theorem 1Whenk >0,there is noω(h)onO(-k)with positive holomorphic bisectional curvatures.
The problem here is that ifm >0, we cannot haveB >0 nearU=0.
In [29], there is another functionD=AC-B2.There it was proven thatω(h) has a positive real Riemannian sectional curvature if and only if all of the functionsA,B,CandDare positive.
We could not get any complete K¨ahler metrics with positive holomorphic bisectional curvature, but (on the suggestion of B.Chen) we can get new examples with positive holomorphic sectional curvatures.To do this,we notice that with the sameh,we can defineω(h)on bothCnand inKmonO(-1).Now we ask: assuming thatω(h) has a positive holomorphic bisectional curvature onCn, when does the correspondingω(h) have a positive holomorphic sectional curvature inKm?
The answer to this is that it does if
or ifDh,m′≥0 for somem′<m.
To prove this, we need to calculate the holomorphic sectional curvatures.In our earlier formula for the holomorphic bisectional curvatures, if we letY=X, we get a formula for the holomorphic sectional curvatures.We get that
Therefore, if we let|x1|2+|x2|2= 1,t=|x1|2,t ∈[0,1], the holomorphic sectional curvature is positive if
is positive.The reason for this is that, by our assumption onφand the result fromCn, whenm=0, this is always nonnegative (actually positive ifU/=0).We only need to prove that the sum of the rest of terms, i.e., those terms withm, is positive.This is true ifDh,mis positive or ifDh,m′is nonnegative for somem′<m.
We notice thatφUUis negative and thatφUcannot be negative.Otherwise,φwill be zero beforeUgoes to infinity.By 2dU=hdr, the condition (2) is just
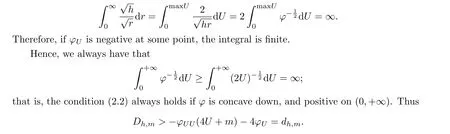
Therefore, ifdh,m ≥0, then the holomorphic sectional curvature is positive.
From the above, we get the sufficient conditions as follows:
Theorem 2 Assuming thatUis a smooth function on [0,+∞), thatφis a concave function ofUsatisfyingφU >0,φ(0)=0,φU(0)=2, and thatm >0 is a constant,
IfDh,m >0 orDh,m′≥0 for somem′<m,the metricsω(h)ofO(-1)have positive holomorphic sectional curvatures.
We also have
Theorem 3 Assume thatUis a smooth function on[0,+∞),thatφis a concave function ofUsatisfying thatφU >0,φ(0)=0,φU(0)=2, and thatm >0 is a constant,
Ifdh,m >0 ordh,m′≥0 for somem′<m,the metricsω(h)ofO(-1)have positive holomorphic sectional curvatures.
Remark 1 Theorems 2 and 3 give the sufficient conditions for complete K¨ahler metrics with positive sectional curvatures onO(-1) We will give some examples of complete K¨ahler metrics with positive holomorphic sectional curvatures in the next section.
This serves as the cases for the line bundleO(-1).However,these two Theorems seemingly do not supply a method for finding complete K¨ahler metrics with positive holomorphic sectional curvatures onO(-k) withk >1.

Now,φkandUksatisfy Corollary 1.Therefore, we can apply Corollary 1 after replacing these byφandU.That is, with the new notation, we have that
As before, we have that-φUU,φ-UφU,2U-φare nonnegative.
Therefore, as above, the holomorphic sectional curvature is positive if

If, (1)Dh,m,k,s >0 orDh,m′,k,s ≥0 for somem′<m, and (2),k(k-1)φ <sm, the metricsω(h) ofO(-k) with an integerk >1 have positive holomorphic sectional curvatures.
We also have
Theorem 3′Assume thatUis a smooth function on [0,+∞), thatφis a concave down function ofUsatisfying thatφU >0,φ(0)=0,φU(0)=2, and thatm >0 is a constant,

The first condition can be achieved byφhaving an asymptoticy=aU+b.
Therefore, we have
Theorem 2′′Assume thatUis a smooth function on [0,+∞), thatφis a concave down function ofUsatisfying thatφU >0,φ(0)=0,φU(0)=2, and thatm >0 is a constant,
If, (1)Dh,m,k,s >0 orDh,m′,k,s ≥0 for somem′<m, and (2.2),k2φ <2kU+sm, the metricsω(h) ofO(-k) with an integerk >1 have positive holomorphic sectional curvatures.
We also have
Theorem 3′′Assume thatUis a smooth function on [0,+∞), and thatφis a concave down function ofUsatisfying thatφU >0,φ(0)=0,φU(0)=2, thatm >0 is a constant,
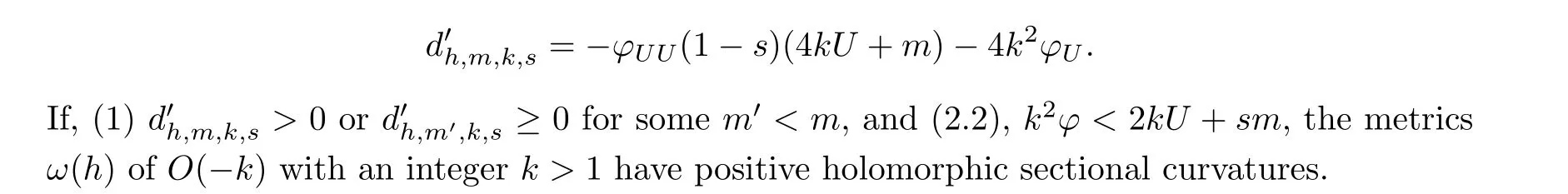
To apply these last four Theorems, it is natural to find examples with an asymptote in both cases where one is a horizontal asymptote and the other one is a slant asymptote.
Since our metric isU(n) invariant, everything is a function ofr=|z|2.However,ris not directly a part of a complex coordinate other than as a quadratic function.This does not describe the fiber of the C*bundle.Therefore, we shall use a better parameter.There is a natural coordinate changez= ewfor the C*part, i.e., outside the zero section.Lettings=Rew, thenr=e2sand
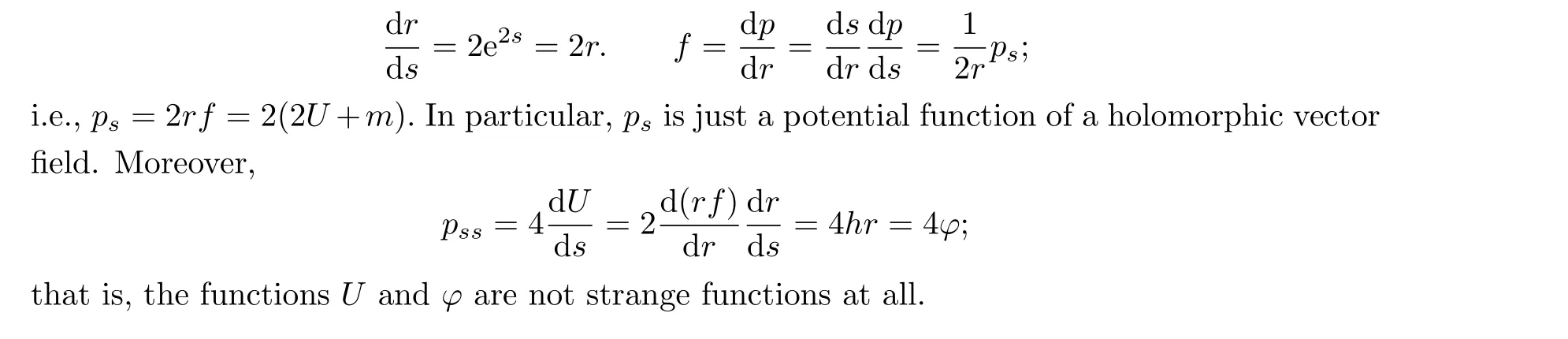
3 Complete K¨ahler Metrics with Positive Holomorphic Sectional Curvatures on O(-1)
In this section, we will discuss the examples of complete K¨ahler metrics with positive holomorphic sectional curvatures onO(-1), and we also give the asymptotes of the functionφ(U) for these examples.
3.1 Metrics with a φ(U) Without an Asymptote
We now solvedh,m=0.Lettingy=φU, we then get that
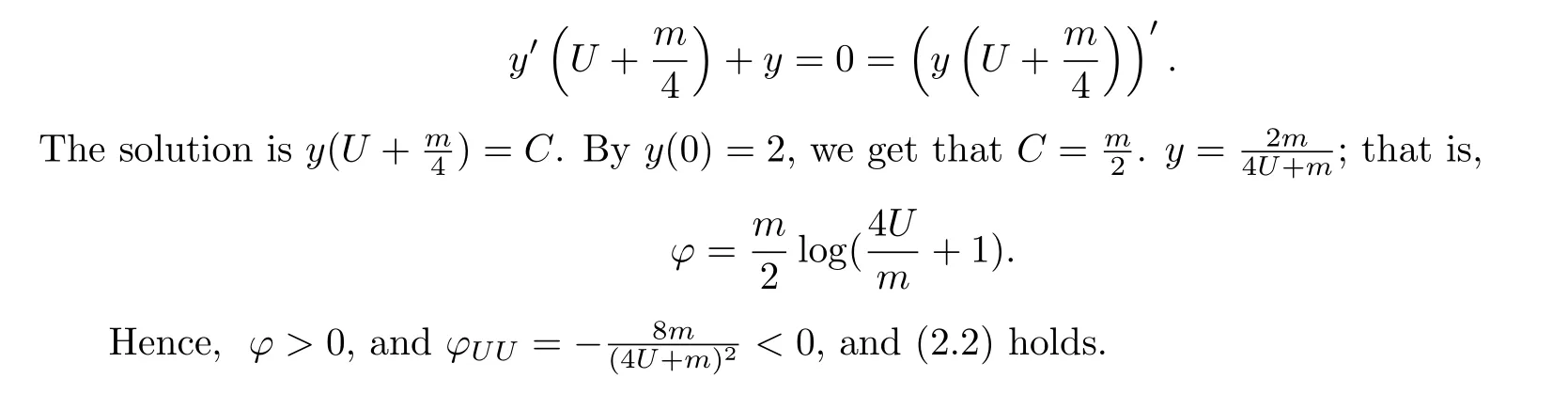
Theorem 3.1.1 Ifdh,m′= 0 withm′<m, then the metrics overO(-1) have positive holomorphic sectional curvatures.

Remark 3.1.2 In this case, lettingU →+∞, we have thatφ →+∞, andφdoes not have any asymptote.
3.2 Metrics with a φ(U) with a Horizontal Asymptote
We now solve



In this case,we can check thatφU >0,φUU <0.As a result,we get the following theorem:
Theorem 3.2.2 Ifdh,m=αUφU, then the corresponding solution overO(-1) has positive holomorphic sectional curvatures withα >0.
Next, we consider another case.
Theorem 3.2.3 Ifdh,m=4(dφU+f(-φUU)), then the corresponding solution

3.3 Metrics with a φ(U) with a Slant Asymptote
Next we will consider some slant asymptotic cases, which are the most important and the most difficult cases that we need to obtain.
If-φUU(4U+m)- 4φU=e+gφU+l(-φUU), then lettingy=φU, we have that-y′(4U+m-l)=e+(4+g)y, whereecan take the negative number.
Denote thatm-l=l0, 4+g=g0.We can then get thatg0>0, and therefore,
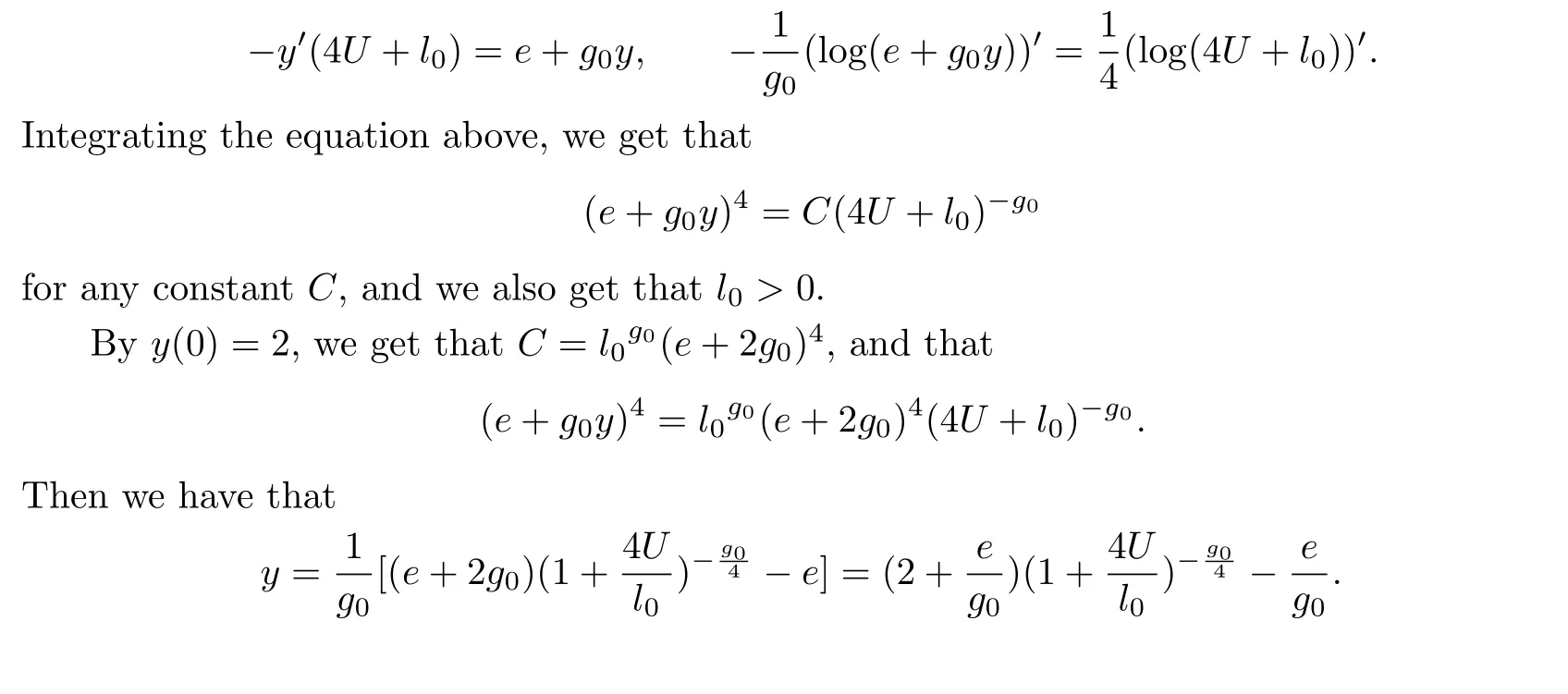

Now we check the possibility of the holomorphic sectional curvature being nonnegative in this case.
Summarizing the above, we get
Lemma 3.3.1 Ifdh,m=e+gφU+l(-φUU), then the corresponding solution has a form


Because 2-E=kFG >0, we just need thatm-F ≥0, i.e.,m ≥F.Therefore,



As a result, we just need 2k- 4≥0; that is,k ≥2.Then we can get the positive holomorphic sectional curvatures, as desired.
Theorem 3.3.1 Ifdh,m=e+gφU+l(-φUU), then the corresponding solution

3.4 More Metrics with a φ(U) with a Horizontal Asymptote
We know that in Theorem 3.2.2,dandfare positive constants.However,fcan take a negative value.


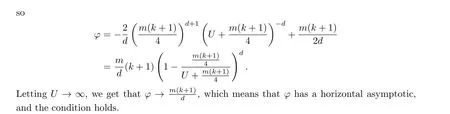
3.5 More Examples
According to Corollary 1 and the sectional curvature in Section 2, we can get that

See also the Corollary 3.9 in [32].
4 Complete K¨ahler Metrics with Positive Holomorphic Sectional Curvatures on O(-k) with k >1
Now we want to construct some examples of complete K¨ahler metrics with positive holomorphic sectional curvatures onO(-k) withk >1, using Theorem 3′from the second section.To do this, we apply the example from Theorem 3.2.1.We solve the equation
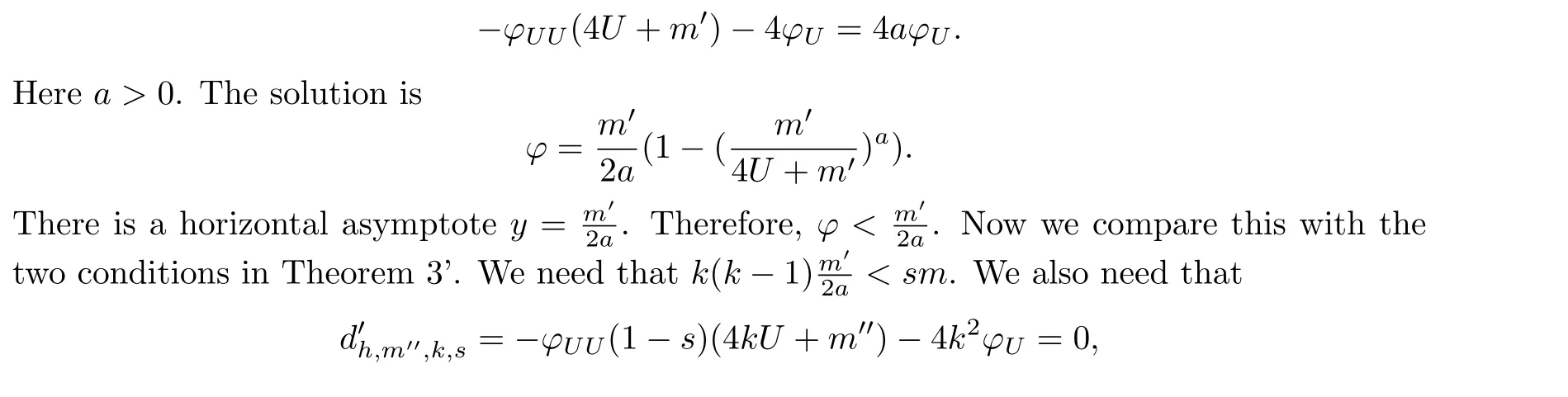
withm′′<m.To say that these conditions are satisfied by our solution, we need that the two equations are the same.We have that

Theorem 4There are manyφwith a horizontal asymptote which give complete K¨ahler metrics with positive holomorphic sectional curvatures onO(-k) withk >1.
This in particular proves our Main Theorem.Similar results with solutions without an asymptote or with a slant asymptote have been obtained in [12].
AcknowledgementsWe would like to thank Professors Feng, Han and the School of Mathematics and Statistics, Henan University for their support.The second author thanks Professor Peter Li for giving a talk related to this topic when the second author was at UC Riverside, and for his support with [7].He also thanks Professor X.Zhu for giving a talk at a conference in China, which led him to this problem.Thanks also go to Professor B.Chen for his encouragement.We also take this opportunity to thank Professor Francis Zheng for sending us his paper [29], which is not easy to acquire in China.We also appreciate the constructive comments and suggestions from the referees, which made this paper much more readable.
Conflict of InterestThe authors declare no conflict of interest.
 Acta Mathematica Scientia(English Series)2024年1期
Acta Mathematica Scientia(English Series)2024年1期
- Acta Mathematica Scientia(English Series)的其它文章
- THE RIEMANN PROBLEM FOR ISENTROPIC COMPRESSIBLE EULER EQUATIONS WITH DISCONTINUOUS FLUX*
- THE BOUNDEDNESS OF OPERATORS ON WEIGHTED MULTI-PARAMETER LOCAL HARDY SPACES*
- AGGREGATE SPECIAL FUNCTIONS TO APPROXIMATE PERMUTING TRI-HOMOMORPHISMS AND PERMUTING TRI-DERIVATIONS ASSOCIATED WITH A TRI-ADDITIVE ψ-FUNCTIONAL INEQUALITY IN BANACH ALGEBRAS*
- INTERFACE BEHAVIOR AND DECAY RATES OF COMPRESSIBLE NAVIER-STOKES SYSTEM WITH DENSITY-DEPENDENT VISCOSITY AND A VACUUM*
- CONVEXITY OF THE FREE BOUNDARY FOR AN AXISYMMETRIC INCOMPRESSIBLE IMPINGING JET*
- SOME PROPERTIES OF THE INTEGRATION OPERATORS ON THE SPACES F(p,q,s)*
