Quantum geometric tensor and the topological characterization of the extended Su–Schrieffer–Heeger model
Xiang-Long Zeng(曾相龍), Wen-Xi Lai(賴文喜), Yi-Wen Wei(魏祎雯), and Yu-Quan Ma(馬余全)
School of Science,Beijing Information Science and Technology University,Beijing 100192,China
Keywords: quantum geometric tensor, topological Euler number, Chern number, Berry curvature, quantum metric,Su-Schrieffer-Heeger(SSH)model
1.Introduction
The Su-Schrieffer-Heeger (SSH) model is a topological quantum system model with a simple structure, but distinct topological properties.[1-6]These include a winding number that characterizes the topological properties and the correspondence between bulk and edge states.[7-11]In addition, SSH models can be used to describe one-dimensional polyacetylene, graphene ribbons, p-orbital light ladder systems[12,13]and off-diagonal two-color optical lattices.[14]Historically,the Haldane model introduced a next-nearest neighbor(NNN)interaction into a two-dimensional honeycomb structure to realize the anomalous quantum Hall effect.[9]This caused the system to undergo a topological phase transition from an ordinary insulator to a Chern insulator.Interestingly, if we expand the SSH model by adding appropriate cyclic modulation parameters, we can obtain a phase diagram similar to the two-dimensional Haldane model,[15]which further enriches the theoretical value of the one-dimensional SSH model and can be used to simulate two-dimensional topological systems.[16-20]The parameters of the modulated SSH model can be obtained through existing experimental techniques involving cold atoms, optical setups or waveguide systems,[21-24]such as the interaction of fermion atoms on a two-legged ladder.[13]These results can be verified by using existing experiments.
As a general covariant tensor in Hilbert space geometry,the quantum geometric tensor(QGT)defined on a parameterized quantum state manifold is expected to shed some light on the quantum phase transitions in manybody systems.[27-29]Its imaginary part (up to a coefficient)corresponds to the Berry curvature, which is a key quantity to derive the first Chern number in order to understand the topological aspects of quantum matter.Especially, the quantum metric (real part of the QGT) proposed by Provost and Valee[25]is a positive semi-definite Riemannian metric,which defines a gauge-invariant distance between two adjacent quantum states in a parameterized Hilbert space.Recently, it was shown that the quantum metric plays a crucial role in quantum transport phenomena,quantum noise,optical conductivity,the anomalous Hall effect, unconventional superconductivity and related topics.[30-57]Furthermore,it has been revealed that the quantum metric can provide a topological Euler number for the energy band.This is based on the Gauss-Bonnet theorem applied to the topological characterization of the closed Bloch state manifold in the first Brillouin zone, which provides an effective topological index for a class of nontrivial topological phases.[58-72]
This paper is structured as follows.In Section 2,we study a cyclically modulated SSH model with long-range hopping terms and solve its Hamiltonian in the Bloch momentum space with periodic conditions.In Section 3,we obtain the QGT for the occupied lower band of the extended SSH model.The critical points in the model can be witnessed by the singularity behaviors of the Berry curvature and the quantum metric.In Section 4,we study the topological Euler number of this model and compare the phase diagrams marked by the Chern and Euler numbers, respectively.Finally, we provide a summary of our work.
2.The model
We consider the SSH model withNlattice points, the Hamiltonian can be written as[6]
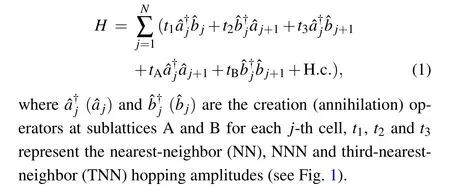
Fig.1.The extended SSH model of long-range interactions.
Now,we modulatet1andt2as

whereφis an additional parameter used to adjust the strength relation betweentAandtB.Then we consider the periodic boundary conditions and introduce the following Fourier transformation:

and the eigenvectors are
Here we choose the following modulated extended SSH model of long-range interactions as an example because it has richer topological properties and a higher Chern number topological phase than the ordinary SSH model.In this model,the Hamiltonian of the Bloch state momentum space is
It is obvious that the model is a generalized topological system.Whent3=tA=tB= 0, andt1?= 0,t2?= 0, or whent1(t2) =tA=tB= 0 andt2(t1)?= 0, the system will degenerate into a one-dimensional SSH model,but whent3=0 andtA,tB?=0,the system will become an extended SSH model of NNN interactions.Obviously,fortA=tB=0 andt1,t2,t3?=0,the model is equal to the two-coupled SSH models.
3.Quantum metric, Berry curvature and the quantum geometric tensor
Firstly, we introduce the QGT in the Bloch momentum space.It is derived from the gauge-invariant metric between two states on theU(1) line bundle.We consider two close wave functions in the parameterized Hilbert space|φ(k)〉and|φ(k+δk)〉,wherek=(μ,ν)denotes the Hamiltonian parameters(k,θ)for convenience.The distance between two close wave functions is given by


The direct calculations of quantum metricgμνare tedious;however, it can be verified that there is a simple relation between the quantum metric determinant and the Bloch state|φ(k)〉(for details see the Appendix A in Ref.[57]):

In Fig.2, we show the determinant of the quantum metric detgμνand Berry curvatureFμνas functions of quasimomentumθ,kin the first Brillouin zone,with different modulation parameters.
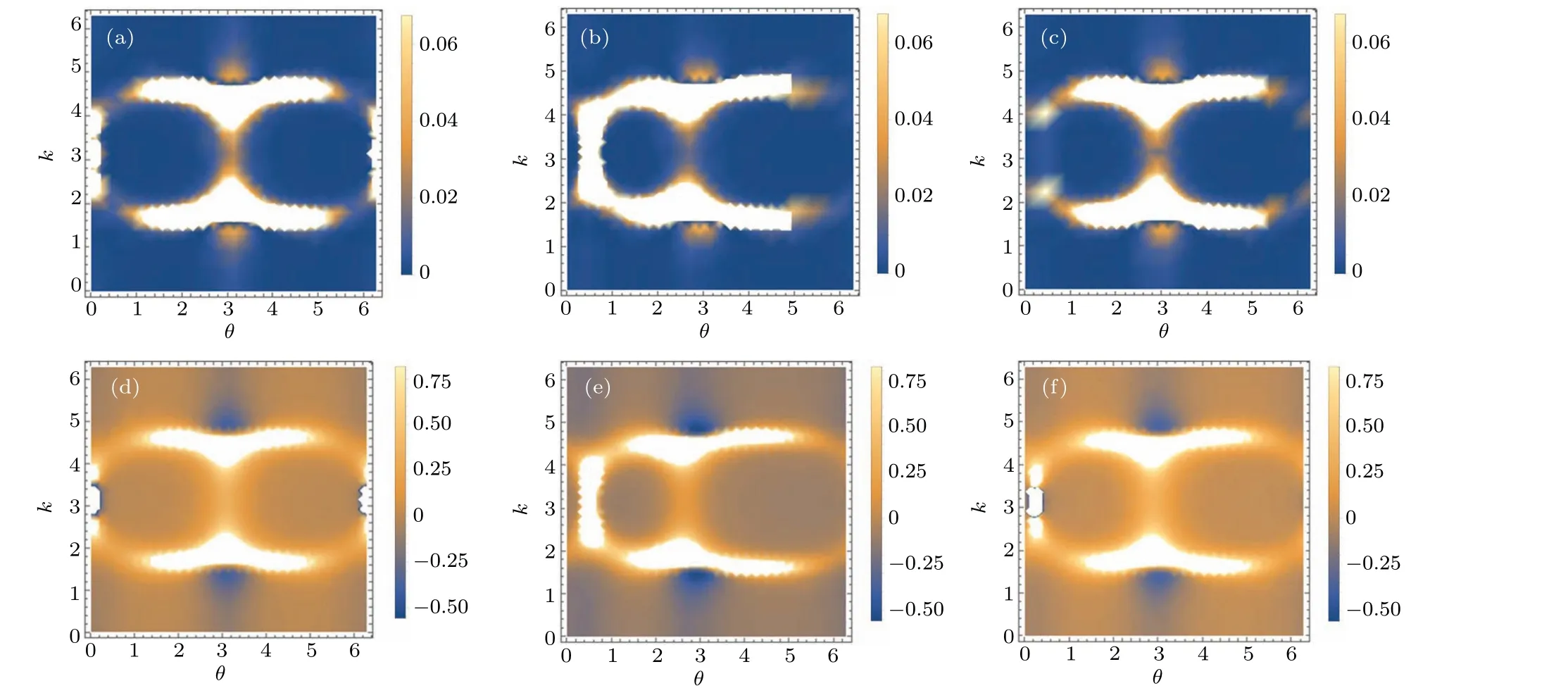
Fig.2.The determinant of the quantum metric detgμν and Berry curvature Fμν as the functions of quasi-momentum θ,k in the first Brillouin zone,with different modulation parameters.(a)detgμν with h=0.2,φ =π/2,t3=0.9.(b)Fμν with h=0.2,φ =π/2,t3=0.9.(c)detgμν with h=1,φ =π/2,t3=1.(d)Fμν with h=1,φ =π/2,t3=1.(e)detgμν with h=0.5,φ =π/2,t3=0.9.(f)Fμν with h=0.5,φ =π/2,t3=0.9.
4.Topological Euler number
In the two-dimensional parameter(μ,ν):=(k,θ)space,the topology of the first Brillouin zone is a two-dimensional torus.Considering the Hamiltonian in the two-dimensional momentum space, the Bloch state|φ(k)〉 will adiabatically evolve aU(1) line bundle.The first Chern number, which serves as a topological invariant for all filled bands,can be obtained by integrating the imaginary part (Berry curvature) of the QGT over the Brillouin zone
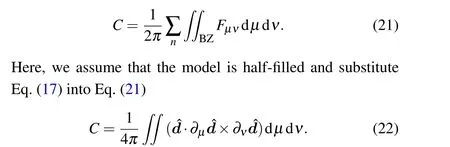
As shown in Fig.3, the model can exhibit different topological phases with higher Chern numbers by varying the NNN hopping term and it undergoes the corresponding topological quantum phase transitions.
The topological Euler numbers can be derived from the Gauss-Bonnet theorem based on the quantum metric(real part of the QGT)
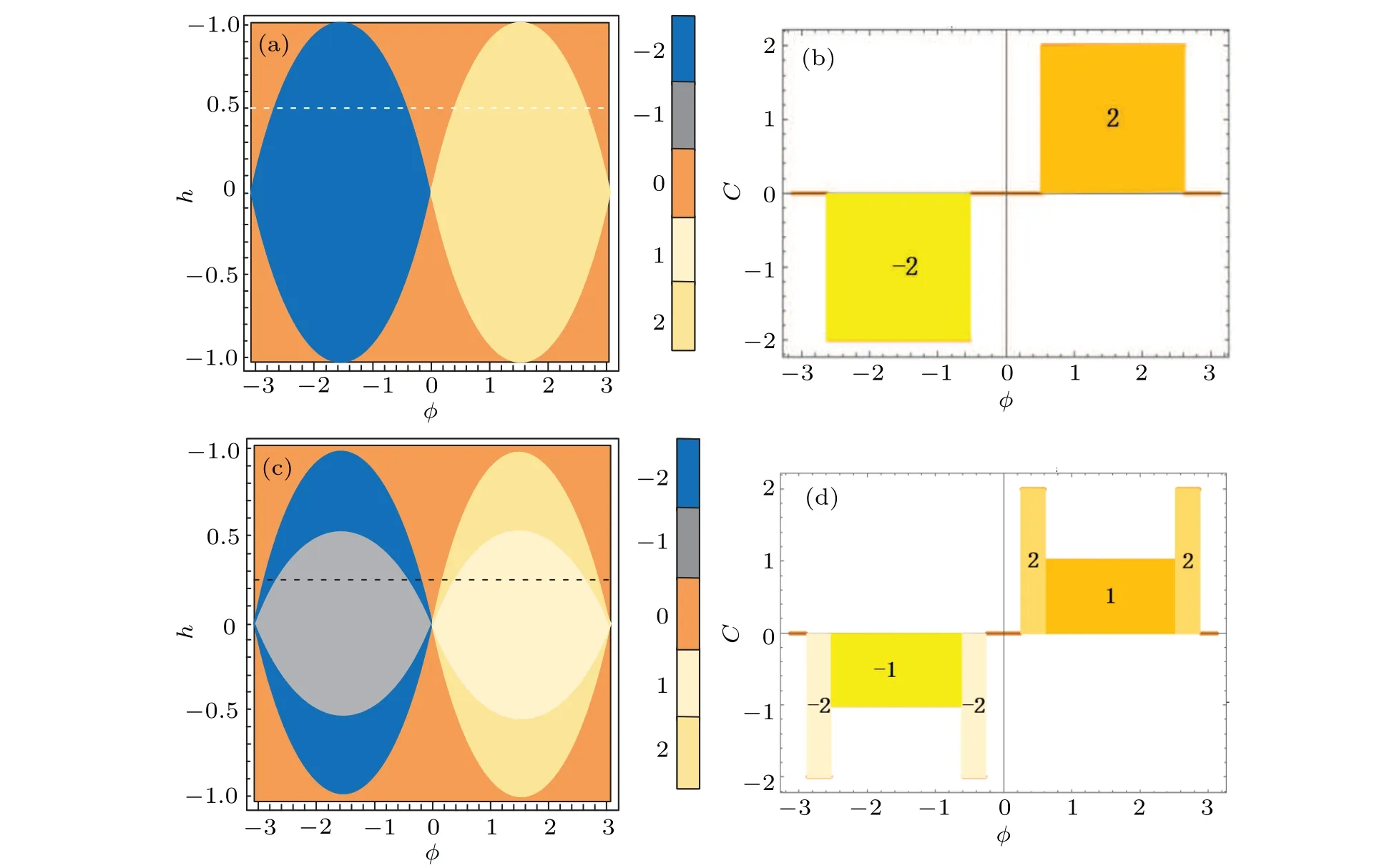
Fig.3.The Chern number varies with the parameters h and φ, and the other parameters are set to (a)t3 =1.(b) The Chern number for the white line in(a)where h=1/2 with φ ∈(-3,3).(c)t3=0.9.(d)The Chern number for the white line in(a)where h=1/4 with φ ∈(-3,3).
whereκ=Rμνμν/detgis the Gauss curvature and dA=(detg)1/2dμdνdenotes the measured area according to the metricgandRμνμνis the covariant Riemannian curvature tensor.The direct calculation of the Gauss curvature is complicated,but it can be verified that there exists the following relation(for details see Appendix B in Ref.[57])in a generalized two-band Hamiltonian on a 2D manifold asRμνμν=4detg.Then,we generalize Eq.(23)to get the topological Euler number with an energy band in the first Brillouin zone
The results for the topological Euler numbers are shown in Fig.4 with the Hamiltonian of parameterst3=1,h=1/2.
As shown in Fig.4, the Euler number of the lower energy band is not exactly equal to 4 in the topological nontrivial phase where the first Chern number =±2.The reason for this is that the quantum metric tensor is actually positive semidefinite.In a general two-dimensional two-band system,it can be proven that(for more details see Ref.[73]): (1)If the phase is topologically trivial, then the quantum metric must be degenerate - det(g)=0 in some region of the first Brillouin zone.This leads to the invalidity of the Gauss-Bonnet formula and exhibits an ill-defined“non-integer Euler number”.(2)If the phase is topological nontrivial with a non-vanishing Berry curvature, then the quantum metric will be a positive definite Riemann metric in the entire first Brillouin zone.Therefore,the Euler number of the energy band is guaranteed to be an even number 2(1-g) by the Gauss-Bonnet theorem on the closed two-dimensional Bloch energy band manifold with the genusg, which provides an effective topological index for a class of nontrivial topological phases.
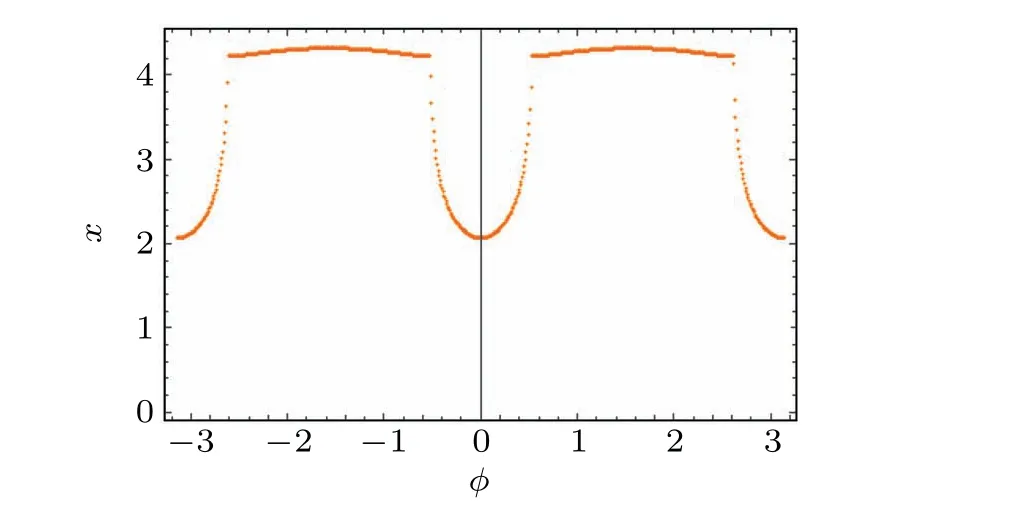
Fig.4.The Euler number varies with the parameter φ and the other parameters are set to t3=1,h=1/2.
5.Conclusion
In summary, we study the QGT and topological Euler number of an extended SSH model with long-range hopping terms.We show that the phase boundaries of the model can be witnessed by the singularity behaviors of both the Berry curvature and the quantum metric.We also study the topological Euler number of this model and make a comparison between the phase diagrams marked by the Chern and Euler numbers, respectively.The degeneracy of the quantum metric in some regions of the first Brillouin zone leads to noninteger Euler numbers.However, the non-integer Euler number can also provide an upper bound for the corresponding Chern numbers.[73]
Appendix A

Acknowledgements
Project supported by the Beijing Natural Science Foundation (Grant No.1232026), the Qinxin Talents Program of BISTU (Grant No.QXTCP C201711), the R&D Program of Beijing Municipal Education Commission (Grant No.KM202011232017), the National Natural Science Foundation of China(Grant No.12304190),and the Research fund of BISTU(Grant No.2022XJJ32).
- Chinese Physics B的其它文章
- A multilayer network diffusion-based model for reviewer recommendation
- Speed limit effect during lane change in a two-lane lattice model under V2X environment
- Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels
- Modeling the performance of perovskite solar cells with inserting porous insulating alumina nanoplates
- Logical stochastic resonance in a cross-bifurcation non-smooth system
- Experimental investigation of omnidirectional multiphysics bilayer invisibility cloak with anisotropic geometry

