Lyapunov Conditions for Finite-Time Input-to-State Stability of Impulsive Switched Systems
Taixiang Zhang , Jinde Cao ,,, and Xiaodi Li ,,
Dear Editor,
This letter studies finite-time input-to-state stability (FTISS) for impulsive switched systems.A set of Lyapunov-based conditions are established for guaranteeing FTISS property.When constituent modes governing continuous dynamics are FTISS and discrete dynamics involving impulses are destabilizing, the FTISS can be retained if impulsive-switching signals satisfy an average dwell-time(ADT) condition.When some or even all constituent modes governing continuous dynamics are not FTISS and discrete dynamics involving impulses are stabilizing, the FTISS can be achieved if impulsive-switching signals satisfy a reverse ADT condition.Examples are presented to illustrate the efficiency of proposed results.
Introduction: Many practical systems can be modeled by hybrid systems which involve both discrete-time and continuous-time behaviors [1], [2].Switched systems and impulsive systems are two general classes of hybrid systems.Switched systems involve a finite number of constituent modes and a switching signal orchestrating the switching between them [3], while impulsive systems depict real world processes that generate instantaneous state resets at discrete times [4].Impulsive switched system, as a more comprehensive dynamical system, involves impulses and switching in a single framework [5].Such system, as it is known, does not retain the property of constituent mode.Besides, the impulses governing the instantaneous state changes often divide into two classes: destabilizing impulses and stabilizing impulses [6], [7].In that scenario, a suitable choice of impulsive-switching signal plays an important role in guaranteeing stability or robustness for impulsive switched systems.
Input-to-state stability (ISS) characterizes an asymptotic convergence behavior of solutions with external inputs.Roughly speaking,ISS includes an asymptotic stability of the solutions in the absence of external inputs and an asymptotic gain property with respect to external inputs [8]–[10].Finite-time stability, having a faster rates of convergence time than asymptotic stability, requires that the solutions reach to equilibrium point during a finite time interval [11]–[14].The settling time, however, typically is unknown and depends on the initial conditions.Combining the properties of ISS and finite-time stability, [15] introduced a concept of FTISS for continuous-time systems.The theory of FTISS has proved very useful not only in the analysis of input systems, but also in the design controllers and observers of control systems.Surprisingly, there has been little FTISS results on dynamic systems up to now, see [16]–[18].Notice that although the impulse and switching are considered in [17], [18],those results only considered the case of stable continuous dynamics with destabilizing impulses.More importantly, a detailed analysis of the settling time has not been carried out in these existing works.
This letter focuses on FTISS of impulsive switched systems.Some sufficient conditions, which rely on a relation among continuous dynamics, impulsive actions, and external input, are presented.The main contributions are threefold: 1) The constituent modes governing continuous dynamics, which may or may not be FTISS, are seriously taken into account; 2) Regarding the impulsive actions in discrete dynamics, two classes of impulses including destabilizing impulse and stabilizing impulse are considered, respectively; 3) A precise estimation of settling time, whenever external inputs are absent, can be deduced under certain impulsive-switching signals.
Problem statement: Consider the impulsive switched system



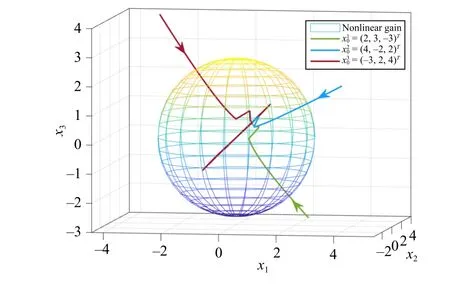
Fig.1.Simulation results of Example 1.


Fig.2.Simulation results of Example 2.(a) Trajectories of system (15) and(16) with ζ =0.34 ; (b) Trajectories of system (15) and (16) with ζ =0.88.
Conclusion: This letter studied FTISS for impulsive switched systems involving external inputs affecting both constituent modes and impulsive dynamics.With the help of ADT-like condition, some Lyapunov-based conditions have been proposed with certain classes of impulsive-switching signals.Moreover, a precise formulation of settling time, whenever external inputs are absent, has been achieved under the designed impulsive-switching signals.
Acknowledgments: This work was supported by the National Natural Science Foundation of China (61833005).
 IEEE/CAA Journal of Automatica Sinica2024年4期
IEEE/CAA Journal of Automatica Sinica2024年4期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- When Does Sora Show:The Beginning of TAO to Imaginative Intelligence and Scenarios Engineering
- Goal-Oriented Control Systems (GOCS):From HOW to WHAT
- Digital CEOs in Digital Enterprises: Automating,Augmenting, and Parallel in Metaverse/CPSS/TAOs
- A Tutorial on Federated Learning from Theory to Practice: Foundations, Software Frameworks,Exemplary Use Cases, and Selected Trends
- Cybersecurity Landscape on Remote State Estimation: A Comprehensive Review
- Data-Based Filters for Non-Gaussian Dynamic Systems With Unknown Output Noise Covariance
