Synchronization of Drive-Response Networks With Delays on Time Scales
Yanxia Tan and Zhenkun Huang
Dear Editor,
This letter deals with the synchronization in drive-response networks with discrete and distributed delays on time scales.Based on the theory of calculus on time scales, Lyapunov functional method and inequality technique, we obtain new sufficient conditions to ensure synchronization criteria which are dependent on boundedness of grainness but independent of the types of delays.Numerical simulations are given to illustrate the effectiveness of our new results.
Recently, the synchronization problem has played a significant role in nonlinear science since its potential applications in image processing, ecological systems, secure communication and harmonic oscillation generation, formation control, etc.[1]-[5].Ways of Synchronization for chaos systems which is applied to communication is investigated in [1].In [2], the authors discuss the synchronization via pinning control on general complex networks.In [3], researchers have studied the sufficient criteria which can ensure the occurrence of synchronization for Lur’e systems.Outer synchronization between drive and response networks via adaptive impulsive pinning control is investigated in [6].An effective control input and a feedback control with an updated law are designed to realize finite-time synchronization between two complex networks [7].
Among the various works of synchronization, continuous-time synchronization [4], [5] and discrete-time synchronization [8] cases are studied respectively.However, in most systems, the interaction among neurons would occur at any time, maybe discrete moments following with continuous-time intervals.Due to the trouble of studying synchronization for continuous-time and discrete-time respectively, it is necessary and meaningful to research them at the same time in neural networks on time scales.The theory of time scales [9] has received a lot of attention recently, which was introduced by Hilger in order to unify continuous and discrete analysis.The field of dynamic systems on time scales links and extends the classical theory of differential and difference equations.Various works have showed that the theory of time scales is an essential tool to deal with many practical problems.Many works concerning the nonlinear systems of differential equation on time scales have been reported in [9], [10] and references therein.However, there are few results dealing with the synchronization of drive-response systems with connection time delays for both discrete and distributed cases on time scales.
As encountered unavoidably in some systems, time delays should be taken into account in the modeling for practical networks.Discrete connection time delays in systems of delayed feedback provide a good approximation in some electronic networks which consist of a small number of neurons.However, due to the presence of parallel pathways with a variety of axon sizes and lengths, a spatial extent exists in biological neural networks which cannot be modeled with discrete time delays.In this case, distributed connection delays are necessary to be used in the models [11].Motivated by the above exposition and existing ones [12], we investigate the exponential synchronization in drive-response networks with discrete and distributed delays on time scales.



Remark 1: As τjiKˉji=1, (10) has the same form as (5) and it is obvious that exponential synchronization of system (1)-(2) and(3)-(4) on time scales is guaranteed by the same criteria.
Remark 2: Synchronization criteria (5) and (10) are dependent on upper bound of grainness.When upper bound of grainness μ ˉ=0, our results includes previous ones [12] as its special cases.As T=Z, the synchronization of coupled systems or drive-response neural networks are investigated in [13].As T =R, (1)-(2) and (3)-(4) reduce to continuous cases, our results lead to ones in [12].
Remark 3: Synchronization of drive-response systems or coupled neural networks in continuous-time (μ(t)=0) are studied in [4], [5],[12] and discrete-time ( μ(t)=1) cases are investigated in [13].This is the first time that we apply the theory of time scales to unify and improve discrete-time and continuous-time neural network under the same frameworks of systems (1)-(2) and (3)-(4).It is well known that few works have been done to study the synchronization of driveresponse systems on time scales, thus the main technique that we use in Theorems 1 and 2 is novel.

It is easy to check that (5) holds.Then, fort∈[0,+∞)T=P1,1, the state trajectory ofx(t) andy(t) with exponential synchronization can be observed in Fig.1.
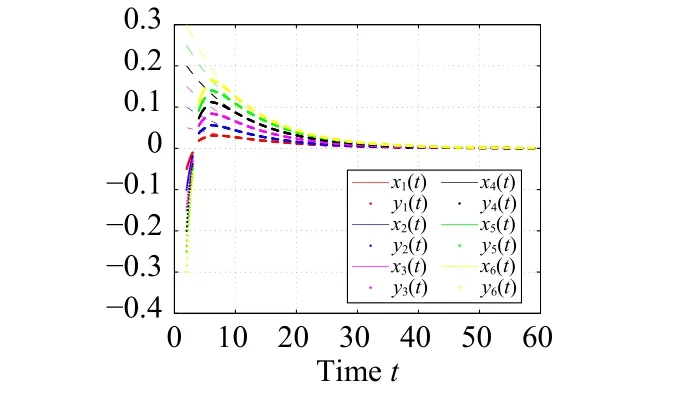
Fig.1.The state trajectory of system (1)-(2) with T =P1,1.

with the functions
It is easy to check that (10) holds.Then, fort∈[0,+∞)T=P1,1, the state trajectory ofx(t) andy(t) with exponential synchronization can be observed in Fig.2.
Conclusion: In this letter, by using the Lyapunov functional method and inequality technique, we have derived new sufficient criteria to ensure the synchronization of systems (1)-(2) and (3)-(4) on time scales.Both continuous-time and discrete-time synchronization are studied in a unified framework (1)-(2) and (3)-(4) as well as the connection time delays are of discrete or distributed cases.Our numerical results have proved that our results obtained in this letter are effective and the method utilized in this letter can be served as a universal framework for the research of other dynamic systems on time scales.
Acknowledgments: This work was supported by the National Natural Science Foundation of China (61573005).
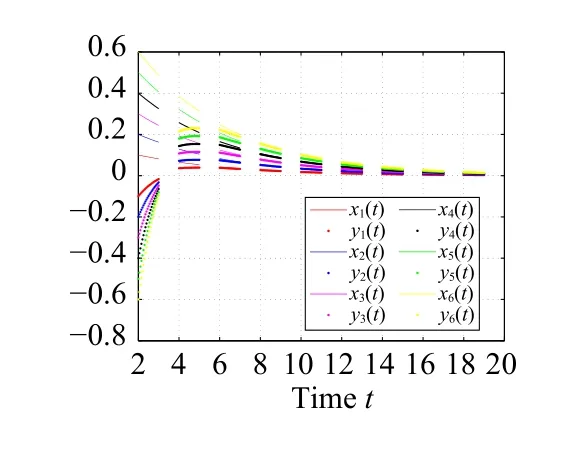
Fig.2.The state t rajectory of system (3) and (4) when T =P1,1.
 IEEE/CAA Journal of Automatica Sinica2024年4期
IEEE/CAA Journal of Automatica Sinica2024年4期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- When Does Sora Show:The Beginning of TAO to Imaginative Intelligence and Scenarios Engineering
- Goal-Oriented Control Systems (GOCS):From HOW to WHAT
- Digital CEOs in Digital Enterprises: Automating,Augmenting, and Parallel in Metaverse/CPSS/TAOs
- A Tutorial on Federated Learning from Theory to Practice: Foundations, Software Frameworks,Exemplary Use Cases, and Selected Trends
- Cybersecurity Landscape on Remote State Estimation: A Comprehensive Review
- Data-Based Filters for Non-Gaussian Dynamic Systems With Unknown Output Noise Covariance
