Parameter-Free Shifted Laplacian Reconstruction for Multiple Kernel Clustering
Xi Wu , Zhenwen Ren , and F.Richard Yu
Dear Editor,
This letter proposes a parameter-free multiple kernel clustering (MKC)method by using shifted Laplacian reconstruction.Traditional MKC can effectively cluster nonlinear data, but it faces two main challenges: 1) As an unsupervised method, it is up against parameter problems which makes the parameters intractable to tune and is unfeasible in real-life applications; 2) Only considers the clustering information, but ignores the interference of noise within Laplacian.To solve these problems, this letter proposes a parameter-free shifted Laplacian reconstruction (PF-SLR)method for MKC, relying on shifted Laplacian rather than traditional Laplacian.Specifically, we treat each base kernel as an affinity graph,and construct its corresponding shifted Laplacian with only low-frequency components.Then, by convex combination reconstructing a highquality shifted Laplacian, PF-SLR can preserve the energy information and clustering information on the largest eigenvalues simultaneously.After that, the cluster assignments can be obtained by performingkmeans on the co-product, without any parameters involved throughout the whole process.Compared with eight state-of-the-art methods, the effectiveness and feasibility of our method are verified.
Introduction: As we know, clustering is a significant tool for data mining, machine learning and other communities [1], [2], which aims to partition data into disjoint clusters relying on the similarity between samples.However, plentiful clustering methods are tricky to deal with nonlinear data [3].Exactly, MKC is a milestone role for handling nonlinear data, it needs a set of predefined base kernels, and then integrates them into a consensus kernel for clustering.Also, MKC can yield better performance than that of single kernel methods, and can avoid users to select and tune kernel parameters [4].
The most prevalent MKC methods are based on spectral graph learning, which learn an affinity graph and employ spectral clustering to obtain the results [5].According to spectral graph theory, such methods mainly use the spectrum of Laplacian to identify the clusters, and the relaxed solution of the crispy clusters is given by the minimum eigenvectors of Laplacian.They have achieved conspicuous performance, but thorny problems still remain.For example, [6] uses anchor strategy to reduce complexity, but it ignores the energy loss and may contain noise effect; [7] directly learns a Laplacian via Laplacian reconstruction, while the contradiction between preserving the energy information and clustering information inevitably decreases the performance; [8] is a parameterfree MKC method, but its performance relies on the manner of consensus kernel learning, which is exactly a stumbling block.
In this letter, a parameter-free MKC method is proposed to deal with the above problems, dubbed as PF-SLR for multiple kernel clustering.Specifically, treats each kernel as an affinity matrix and then obtainsrrank shifted Laplacian by introducing a low-pass filter.After that, theser-rank shifted Laplacians are used to reconstruct a true shifted Laplacian,where the reconstruction energy and clustering information can be preserved simultaneously.The clusters can be obtained by performingkmeans on the co-product (i.e., eigenvectors with the most abundant information) produced in the optimizing algorithm of PF-SLR.
Related work:

Contradictory discovery and solution:
1) Discovery: As shown in Fig.1, when performing Laplacian reconstruction, the energy information and the small reconstruction loss are in the largest eigenvalues, i.e., the energy information of LiSin (3) and (4) is preserved in the largest eigenvectors.However, according to (2), the clustering information is embedded in the smallest eigenvectors of LS.Thus, there is a contradictory discovery that reconstructing Laplacian is a contradiction with preserving cluster information.
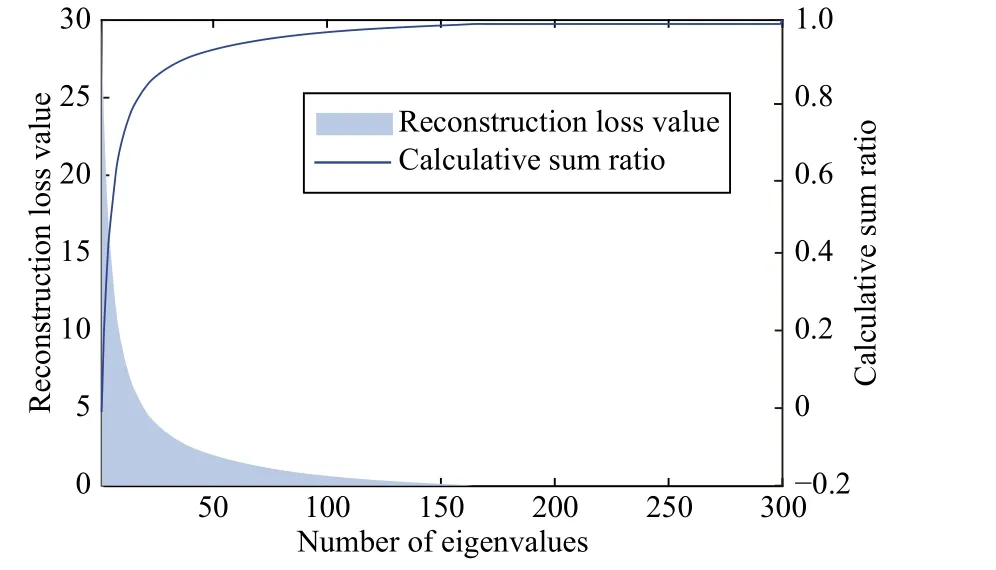
Fig.1.The obtained eigenvalues distribution of Laplacian via Gaussian kernel function on Yale dataset, where the eigenvalues are sorted with decreasing order.
2) Solution: To solve the contradiction, we propose a Laplacian learning paradigm via
It is effortless to see that thecsmallest eigenvalues of LSare corresponding to theclargest eigenvalues of L, so the clustering information can be given by theclargest eigenvectors of L.Considering the shift of cluster information on eigenvalues, we name L as shifted Laplacian.Thus L can perform reconstruction and encode clustering information, so as to solve contradiction exactly.
Objective function:
1) Shifted Laplacian reconstruction: For MKC, given a set of kerneleach Kpis regarded as an affinity graph rather than a plain kernel, so its normalized Laplacian can be easily obtained by graph spectral theorem.To delete the redundant edges of each graph,kis usually used to control the number of neighbors of nodes.Define Lpas the shifted Laplacian of Kp, it can be given by

Overall, PF-SLR is quietly straightforward to implement, and the advantages can be summarized as follows:
a) Parameter-free: As we known, the number of parameters is crucial for unsupervised methods, especially for clustering task.PF-SLR obtains the reconstructed shifted Laplacian without any parameters contained.
b) Consider both clustering information and energy preservation: PFSLR proposes to reconstruct a shifted Laplacian, such that the main energy and clustering information can be obtained, and the noise effects are minimized.
c) True Laplacian: As PF-SLR uses the convex combination to reconstruct the shifted Laplacian, such that obtains a true Laplacian mathematically, which can naturally apply spectral graph theorem and has a positive effect on the clustering performance.
2) The optimal solution: Since the subproblems of (10) have the closed-form solutions, the coordinate descent method can be applied to find the optimal solutions.
a) For αp: Assuming other variables are constant, the convex combinatio n αpof (10) is updated via
it can be further written as

Consequently, the optimization is completed and the co-product U is obtained, which is the informative eigenvectors (i.e., indicator matrix).And thenk-means is used to discretize U to get the final clustering results.The specific steps for optimization are exhibited in Algorithm 1.
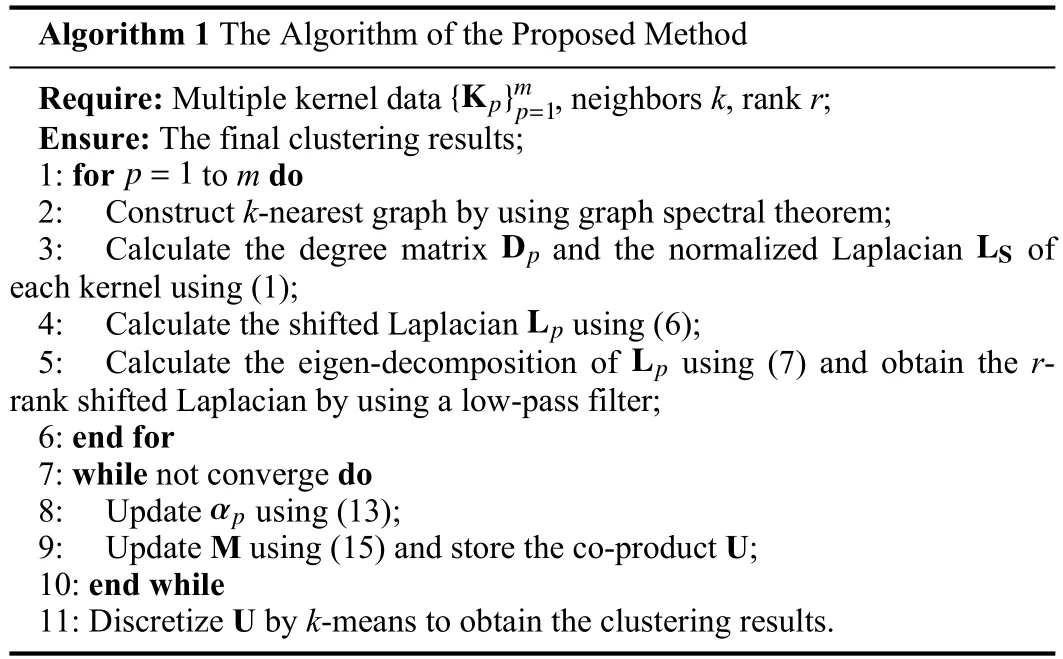
Algorithm 1 The Algorithm of the Proposed Method{Kp}mp=1 Require: Multiple kernel data , neighbors k, rank r;Ensure: The final clustering results;p=1 1: for to m do 2: Construct k-nearest graph by using graph spectral theorem;Dp LS 3: Calculate the degree matrix and the normalized Laplacian of each kernel using (1);Lp 4: Calculate the shifted Laplacian using (6);Lp 5: Calculate the eigen-decomposition of using (7) and obtain the rrank shifted Laplacian by using a low-pass filter;6: end for 7: while not converge do αp 8: Update using (13);9: Update M using (15) and store the co-product U;10: end while 11: Discretize U by k-means to obtain the clustering results.

Rate=k×(c÷m) andS rank=r÷c, tune their ranges to [0.1, 0.15,...,1.5] and [1, 2,..., 5] with step length 0.05 and 1.For fairness, all codes are downloaded from the author’s website and parameters are set based on the corresponding literature.Especially, repeatk-means step 50 times to record the average value for minimizing the impact of initial cluster centers, and the parameter of the diversity term in ONMSC is set to zero.For MLAN and MCLES, we treat the input kernel matrix as plain data to their algorithms.In addition, clustering accuracy (ACC) and average running time (in seconds) are used to indicate the clustering results of all methods.
3) Clustering results: The results are exhibited in Table 1, from which we can obtain: compared with BSKKM, AMKKM and RMKKM, PFSLR achieves superior performance because it has no use for selecting the kernel function; Compared with MLAN and MCLES, the improvement to view kernel matrix as affinity matrix for mining graph information is verified; Compared with CSA-MKC, they can strongly demonstrate PF-SLR considers the effects of reconstruction loss and noise; PFSLR achieves superior performance compared with ONMSC, indicating it can solve the contradiction between reconstruction energy and clustering information; Compared with CoALa, the effectiveness of taking the largest eigenvalues to obtain clustering information and principal energy is validated.In addition, compared to the Laplacian method with parameters (i.e., ONMSC, CoALa), PF-SLR shows the advantage of parameterfree method without tuning parameters in practice, and proves its advantage by using true Laplacian.Besides, the average time of PF-SLR is less than most methods especially CSA-MKC, demonstrating the effectiveness of usingr-rank shifted Laplacian instead of full rank, which can reduce complexity and improve clustering performance.
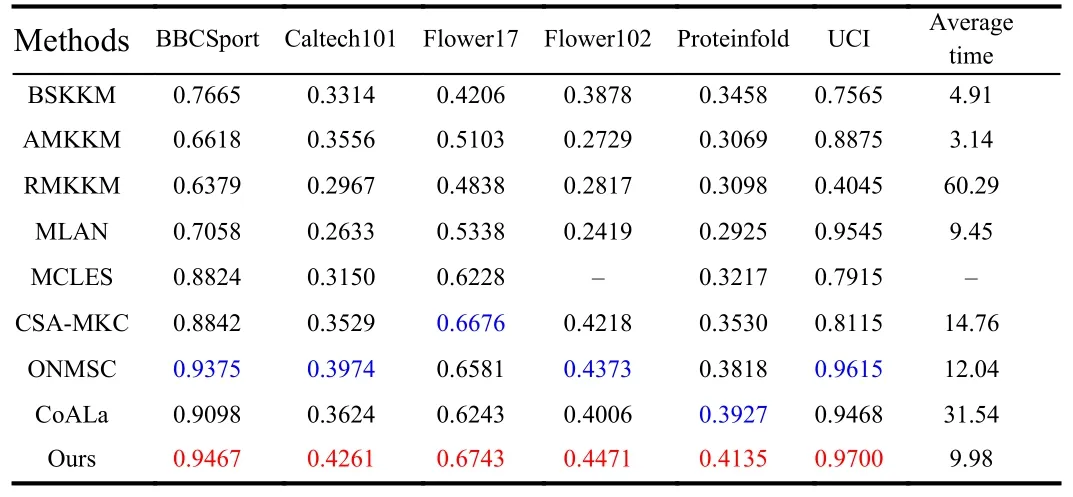
Table 1.ACC and the Average Time of All Methods, Where the Best Results are Marked in Red, Suboptimal Results are Marked in Blue, And “-”Indicates the Failed Results Because Time Costs too Long
4) The influence of initial values and convergence analysis: As shown in Fig.2(a), ACCis stablefor a wide rangeof initial valueskandr,which are straightforward to adjust for MKC method.Andthe experiments on all datasets show that ACC is optimal whenRateis between 0.1 and 0.75, usuallykis set to 2cor 3candris set toc.In other words,a relatively smallkwill yield the best ACC, indicating the ability of the graph can be improved by deleting redundant edges.Moreover, Figs.2(c)and 2(d) shows that the objective value rapidly drop to a flat area after three iterations, demonstrating Algorithm 1 can converge to a stable value.

Fig.2.Performance validation.
5) Study on the effectiveness ofr-rank filtering: In Fig.2(b), it can be clearly observed that ACC ofr Conclusion: This letter proposes a MKC method by adopting the shifted Laplacian without parameters, which uses a convex combination to integrate single shifted Laplacians and introduces a low-pass filter to remove the low-frequency components with low eigenvalues.The filtered high-frequency components are maximized to keep the principal energy of reconstruction and clustering information.Experiments on several datasets and comparisons with other methods confirm the superiority of the proposed method. Acknowledgments: This work was supported by Guangxi Key Laboratory of Machine Vision and Intelligent Control (2022B07), the Open Research Fund from Guangdong Laboratory of Artificial Intelligence and Digital Economy (SZ) (GML-KF-22-04), the Natural Science Foundation of Southwest University of Science and Technology (22zx7101), and the National Natural Science Foundation of China (62106209).
 IEEE/CAA Journal of Automatica Sinica2024年4期
IEEE/CAA Journal of Automatica Sinica2024年4期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- When Does Sora Show:The Beginning of TAO to Imaginative Intelligence and Scenarios Engineering
- Goal-Oriented Control Systems (GOCS):From HOW to WHAT
- Digital CEOs in Digital Enterprises: Automating,Augmenting, and Parallel in Metaverse/CPSS/TAOs
- A Tutorial on Federated Learning from Theory to Practice: Foundations, Software Frameworks,Exemplary Use Cases, and Selected Trends
- Cybersecurity Landscape on Remote State Estimation: A Comprehensive Review
- Data-Based Filters for Non-Gaussian Dynamic Systems With Unknown Output Noise Covariance
