The influence of boundary conditions on the distribution of energetic electrons during collisionless magnetic reconnection
Lei WANG (王磊),Can HUANG (黃燦),*,Dongke CHEN (陳冬可),Zhongwei YANG (楊忠煒),Aimin DU (杜愛民) and Yasong GE (葛亞松)
1 CAS Engineering Laboratory for Deep Resources Equipment and Technology,Institute of Geology and Geophysics,Chinese Academy of Sciences,Beijing 100029,People’s Republic of China
2 College of Earth and Planetary Sciences,University of Chinese Academy of Sciences,Beijing 100029,People’s Republic of China
3 State Key Laboratory of Space Weather,National Space Science Center,Chinese Academy of Sciences,Beijing 100190,People’s Republic of China
Abstract We conducted 2-D particle-in-cell simulations to investigate the impact of boundary conditions on the evolution of magnetic reconnection.The results demonstrate that the boundary conditions are crucial to this evolution.Specifically,in the cases of traditional periodic boundary (PB) and fully-opened boundary (OB) conditions,the evolutions are quite similar before the system achieves the fastest reconnection rate.However,differences emerge between the two cases afterward.In the PB case,the reconnection electric field experiences a rapid decline and even becomes negative,indicating a reversal of the reconnection process.In contrast,the system maintains a fast reconnection stage in the OB case.Suprathermal electrons are generated near the separatrix and in the exhaust region of both simulation cases.In the electron density depletion layer and the dipolarization front region,a larger proportion of suprathermal electrons are produced in the OB case.Medium-energy electrons are mainly located in the vicinity of the X-line and downstream of the reconnection site in both cases.However,in the OB case,they can also be generated in the electron holes along the separatrix.Before the reverse reconnection stage,no high-energy electrons are present in the PB case.In contrast,about 20% of the electrons in the thin and elongated electron current layer are high-energy in the OB case.
Keywords: magnetic reconnection,electron energization,particle-in-cell simulation
1.Introduction
Magnetic reconnection is an efficient mechanism that explosively converts magnetic energy into kinetic and thermal energy of the plasma,causing a topological rearrangement of the magnetic field [1–6].This process is associated with various outburst phenomena in space plasma,such as solar flares [7,8],coronal mass ejections [9],and magnetospheric substorms [10–13].Additionally,reconnection has been fulfilled in dedicated plasma devices [14–16].
The dynamic behavior of electrons is a critical factor in collisionless magnetic reconnection,and the generation of energetic electrons is a significant characteristic of this process [17–19].During antiparallel reconnection,electrons undergo a three-step acceleration process,which includes being trapped by an electrostatic potential well of the polarization electric field and gaining energy due to a pre-acceleration near the inflow separatrices,then being accelerated by the induced electric field in the electron diffusion region,and finally being accelerated during their gradient and curvature drift motion near the magnetic field pileup region [20].Egedalet alsuggested that electrons are pre-accelerated by parallel electric fields distributed along the separatrices before flowing into the reconnection site [21,22].Moreover,electrons can be accelerated along the separatrix multiple times by the parallel electric fields,allowing them to reach relativistic energies [23].In the guide field reconnection,when electrons are funneled into the vicinity of the X-line,they are not demagnetized and gyrate with the force of the guide field,resulting in longer residence time of electrons in the diffusion region and sustained acceleration by the parallel reconnection electric field [24,25].Near the reconnection front or dipolarization front (DF) region,the parallel electric field can trap electrons,causing sustained acceleration by the betatron mechanism [26,27].Additionally,electrons near the DF region can also be significantly accelerated by the Fermi mechanism [28,29].The formation of multiple magnetic islands [30] due to multiple X-line reconnections can lead to electron acceleration during the island coalescence process [31–35].Okaet alfurther discovered that electrons trapped within the islands undergo continuous energization due to the presence of the reconnection electric field prevalent in the reconnection diffusion region [36].Electrons can also gain energy stochastically from the Fermi acceleration mechanism in multiple magnetic islands during reconnection [37].The current sheet linked to a large-scale magnetic island can be fragmented into multiple electronscale current sheets,prompting the generation of secondary magnetic reconnection and resulting in a turbulent state.This process leads to significant electron energization [38–40].
Earlier kinetic simulations of magnetic reconnection typically employ periodic boundary conditions [41–43],which can artificially recirculate particles and magnetic flux and restrict the duration of the physically meaningful results.To overcome this limitation,Daughtonet aldeveloped an appropriate open boundary model to simulate a much larger system and eliminate the artificial effects,allowing the kinetic structure of the reconnection layer to develop over extended periods [44].They found that the electron diffusion region lengthens over time,leading to the electron layer becoming unstable and generating secondary islands periodically.Consequently,the fast reconnection rate is resumed.However,the impact of boundary conditions on the temporal and spatial distribution of energetic electrons at different energy levels under identical plasma and magnetic field parameters remains unclear.In this work,we conducted the first comparative study of the evolution of reconnection and the characteristics of energetic electrons using numerical simulations under periodic and open boundary conditions.
2.Simulation model
In this study,we have simulated the anti-parallel magnetic reconnections via 2-D particle-in-cell (PIC) codes [25,26,45].Apart from the setting of boundary conditions,the remaining components of the simulation model are nearly identical to those used in our previous studies.The simulations start from a Harris current sheet with the number densityn(z)=nb+n0sech2wherenb=0.1n0is the background density and δ=0.5diis the half-width,heredipresents the initial ion inertial length based onn0.Theycomponent of the initial magnetic vector potential is ψ=-δB0lnand the magnetic field is inferred fromB=-ey×?ψ,whereB0is the ambient magnetic field around the current sheet.Ions and electrons follow Maxwellian distribution,with the mass ratio=100 and the initial temperature ratiowhere “i” (“e”) represents ion (electron).The ratio of light speed to Alfvén speed is 15.The typical kinetic energy of a thermal electron is about 0.0476mec2.The electromagnetic fields are updated by Maxwell equations [46],and ions and electrons are treated as individual particles and respond to the electromagnetic fields.The simulations are performed in the (x,z) plane with a domain of [-17.5di,17.5di]×[-9di,9di]and a spatial resolution of 0.025di.The simulations employ more than 108particles in each species.Two cases are run in this study.In the traditional periodic boundary (PB) case,periodic boundary conditions are applied in thexdirection,while fields match the conducting boundary conditions and particles are mirrored at the boundaries in thezdirection.In the fully-opened boundary (OB) case,the particle boundary is identical to the setting in reference [44],and we use a sample of 6 cells to calculate the particle distribution function.Neumann boundary is applied for the electromagnetic fields.Simulations are initiated with a weak local flux perturbation placed at (0,0) [47].The time step is Δt=wheredenotes the ion gyrofrequency.The simulations end att=for each case.
3.Results and discussion
The results of the evolution of magnetic reconnection under two different boundary conditions are displayed in figure 1.Figure 1(a) shows the reconnected magnetic flux and the reconnection electric fieldEy.Magnetic reconnection initiates at aboutt=.Aroundt=,the reconnection rate reaches its peak,exceeding 0.4,indicating that reconnection enters a rapid growth phase.Here,the reconnection rate is represented byEynormalized byVAB0,where Alfvén speedVAis calculated by the peak number density,not the upstream.The fast reconnection may be driven by the selfreinforcing process of the reconnection electric field [48].Beforet=,the evolution of the two cases exhibits striking similarities.However,the evolution diverges significantly afterward.In the PB case,the reconnection electric field drops rapidly and even becomes negative after reaching its maximum.In contrast,in the OB case,the system remains in the fast reconnection stage,withEyranging from 0.25 to 0.45.Figures 1(b) and (c) depict the temporal evolution ofEyalong the linez=0 in the PB and OB cases,respectively.Eypeaks at the outflow front,also known as DF.The evolution appears similar beforet=.In the PB case,Eyin the DF region increases,reaching its maximum of~ 1.3 att=,and then rapidly decreases,even becoming negative.This indicates that the outflows are blocked and the reconnection enters the reverse phase.In contrast,in the OB case,Eyin the DF region continues to increase and reaches its maximum of~ 3.3 att=before the DF propagates out of the simulation domain.This suggests that in the OB case,the amplitude of the DF keeps growing and steepening.
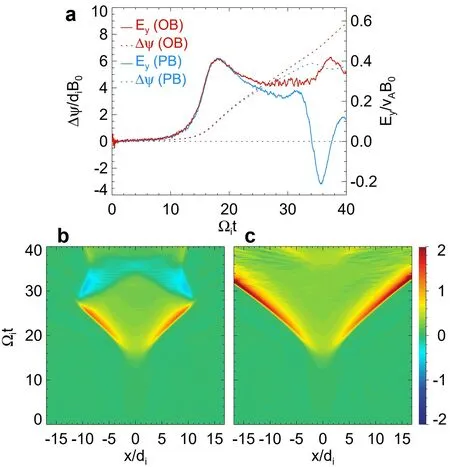
Figure 1.(a) The reconnected magnetic flux (dotted lines) and the reconnection electric field (solid lines) for the PB case (blue) and OB case (red),respectively.The time evolution of reconnection electric field for (b) PB case and (c) OB case along z=0 from t=0 to t=.
Figure 2 illustrates the production of energetic electrons in different energy ranges in the PB case at two typical times(t=and.From top to bottom,the panels exhibit the distribution of electron number densityne,parallel electric fieldE||,reconnection electric fieldEy,and the proportion of suprathermal (0.15mec2<εT<0.4mec2),medium-energy (0.4mec2<εM<1mec2),and high-energy(εH>1mec2) electrons.Att=(in the fast reconnection phase),along the separatrices,the ion-scale parallel electric fields (marked by the arrow in figure 2(b)) in the density depletion layer [49] (the dark blue area in figure 2(a)) accelerate electrons to suprathermal [21,50].In the electron current layer near the X-line,electrons are energized to suprathermal and even medium energy under the DC acceleration ofEy[24,51,52].As electrons move from the reconnection site to the magnetic pile-up region,a significant proportion of suprathermal electrons are accelerated to high energies during their gradient/curvature-drift motion[20,51].Ahead of the DF,thermal electrons are energized to suprathermal mainly by local betatron acceleration [26].The DF serves as the boundary between the background thermal electrons and the accelerated electrons.No high-energy electrons are produced before the end of the fast reconnection phase.Att=,in the reversed reconnection phase,Eybecomes predominantly negative,and DFs are reflected toward the X-line (compared with figures 2(a) and (g)).A significant proportion of medium-energy electrons (peaks at >50%) and high-energy electrons (peaks at >40%) are produced in the pile-up region.
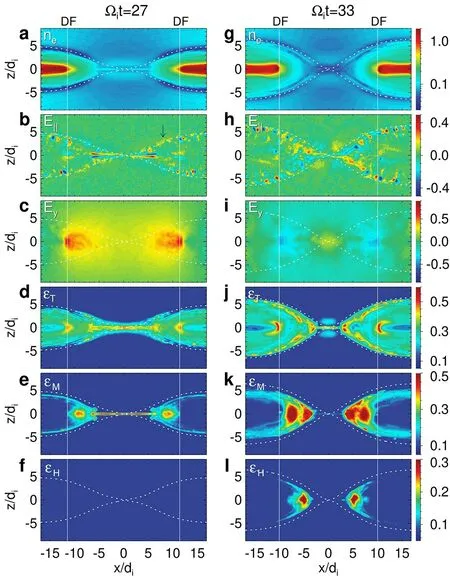
Figure 2.The simulation results from the PB case at t= and t=,respectively.The quantities,from top to bottom,are electron number density ne,parallel electric field E||,reconnection electric field Ey,and proportion of suprathermal electrons,mediumenergy electrons,and high-energy electrons.The black contours in the top panels denote the in-plane magnetic field lines.The white solid (dashed) lines mark the positions of the DF (separatrices).
Figure 3 presents the results of the OB case.Att=,stronger parallel electric fields exist in the density depletion layer compared to the PB case (compared with figures 2(b) and 3(b)),resulting in a larger proportion of thermal electrons being accelerated to suprathermal(compared with figures 2(d) and 3(d)).In the electron current layer near the X-line,electrons are energized to suprathermal and even medium energy via the reconnection electric field.Unlike in the PB case,high-energy electrons can be produced in the OB case,with an average proportion of~ 20% in the fast reconnection phase.The proportion of suprathermal electrons in the pile-up region is similar in both cases,while the PB case has a higher proportion of mediumenergy electrons compared to the OB case.In the OB case,the proportion of suprathermal electrons near the DF is larger than that in the PB case.This is because the DF in the OB case keeps growing (figure 1(c)) with continuous local betatron acceleration.
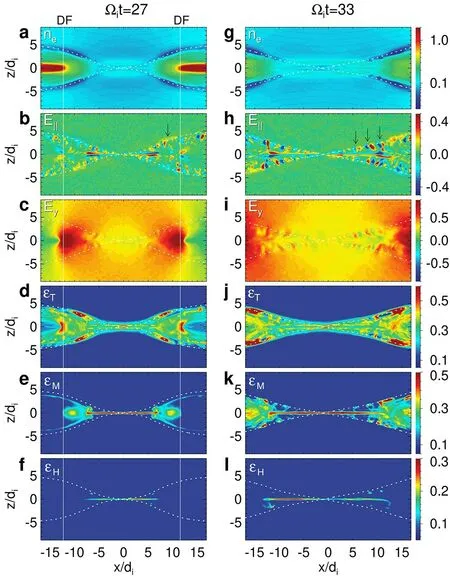
Figure 3.The simulation results from the OB case with the same format as figure 2.
Att=,the DF mentioned above has already propagated out of the simulation domain,while fast reconnection is still ongoing.The electron beam instability leads to the formation of electrostatic solitary structures (arrows in figure 3(h)) or electron phase-space holes (EHs) that propagate rapidly along the separatrices towards the X-line [53–55].As their propagation speed exceeds the phase velocity of the whistler waves,they can excite Cherenkov emission [56],resulting in an electromagnetic perturbation that gradually enhances along the separatrices towards the X-line (Eyperturbation shown in figure 3(i)).This modulates the reconnection rate,which is shown as theEyperturbation aftert=in figure 1(a).The transverse instability traps electrons [57,58],and the reconnection electric field accelerates them from suprathermal to medium energy (figures 3(j)–(k)).As there is no outflow region blocking,the electron current layer can elongate beyond 20di,and high-energy electrons continue to be produced in this region.
Figure 4 provides a quantitative comparison of the production efficiencies of suprathermal electrons (solid curves) and medium-energy electrons (dashed curves)between the PB case (in blue) and the OB case (in red).Before the reconnection rate reaches its maximum,there are no obvious differences between the two cases.Near the separatrix in the PB case,the proportion of suprathermal electrons initially increases slowly and reaches its maximum(~ 23%) att=,and then decreases rapidly.While in the OB case,it increases almost continuously and consistently remains higher than in the PB case aftert=Due to the energization of electrons in the EHs,the proportion of medium-energy electrons is much larger in the OB case.In the pile-up region,the evolution of the proportion of electrons in both energy ranges is similar in the two cases beforet=.Subsequently,the suprathermal electron proportion becomes slightly higher in the OB case,while the medium-energy electron proportion gets higher in the PB case.In the DF region,the proportion of suprathermal electrons in both cases increases almost continuously after the initiation of reconnection,with a slower growth rate aftert=.But the proportion in the OB case surpasses that in the PB case aftert=.The variation trends of the medium-energy electron proportions in the two energy ranges are similar to those in the pile-up region,but the values are smaller.From the separatrix to the DF,the differences between the two cases appear earlier,suggesting that the physics downstream is more susceptible to the influence of boundary conditions.
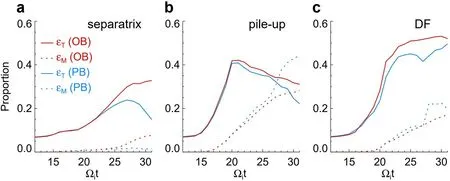
Figure 4.The time evolution of the mean proportion of suprathermal electrons (solid curves) and medium-energy electrons (dashed curves)in the vicinity of (a) separatrix,(b) magnetic pile-up region,and (c) DF region from t= to t=.The blue and red lines represent the results from the PB case and OB case,respectively.Here the separatrix region,the pile-up region,and the DF region are defined as the place where ψ is between ψSP±0.15diB0,between ψPU±0.3diB0,and between ψDF±0.3diB0,respectively.ψSP and ψDF are the y components of the magnetic vector potential at the separatrix and the DF.ΨPU is the mean of ψSP and ψDF.
In the PB case,particles move out from one side of the boundary in thexdirection and reenter the simulation domain from the opposite side multiple times.These reentering particles can go back to the diffusion region and undergo re-acceleration.This process leads to a larger proportion of medium-energy and high-energy electrons (compared with figures 2(k)–(l) and 3(k)–(l)).Additionally,the reconnection outflow and DF are blocked after the system reaches the fast reconnection stage,as illustrated in figure 1(b).In contrast,in the OB case,the DF can propagate out freely.TheBzcomponent continuously strengthens throughout the entire simulation domain,resulting in a consistent increase in the proportion of suprathermal electrons near the DF due to betatron acceleration.This proportion is almost always greater than that observed in the PB case (figure 4(c)).
The OB condition can be used to simulate the substorm process when the magnetic flux in the magnetotail lobe can be continuously replenished to compensate for the reconnected magnetic flux near the reconnection site.However,when the reconnection is faster than the upstream supply,the OB condition used in this study is no longer applicable.In the simulations of reference [56],they used periodic boundary conditions with a large simulation box size ofLx×Ly=200di×30di.Due to the blocking that occurs in the late stage of the evolution of primary reconnection under the PB condition,the simulation domain must be sufficiently large to prevent the artificial recirculation of particles and magnetic flux.However,we found that appropriate OB conditions can produce similar results in a very small calculation domain (meaning low computational cost).This indicates that the OB condition is very suitable for studying local physical processes and therefore has extensive value in application.On the other hand,the PB condition can be applied in certain specific situations,such as in the Earth’s space due to the existence of the dipole field or in experimental devices with closed boundaries,where there is outflow blocking and a reverse reconnection process occurs,producing medium-energy and even high-energy electrons.Additionally,in the magnetic island chain geometry [32,37],electrons can gain kinetic energy by reflecting from the ends of the contracting magnetic islands or by refecting between two approaching magnetic islands.The PB condition is also suitable for this scenario.
4.Conclusion
In conclusion,2-D PIC simulations are conducted to investigate the effects of boundary conditions on magnetic reconnection evolution.Before the fastest reconnection rate is achieved,the evolution is similar between the PB and OB conditions;however,differences emerge afterward.In the PB case,the reconnection electric field rapidly declines and becomes negative sometimes after reaching its maximum,whereas in the OB case,the system remains in the fast reconnection stage.Suprathermal electrons are generated near the separatrix and exhaust region,with more being produced in the OB case in the electron density depletion layer and the DF region.Medium-energy electrons are mainly located in the vicinity of the X-line and downstream of the reconnection site in both cases,but the OB case also generates them in electron holes along the separatrix.Highenergy electrons are absent in the PB case before reverse reconnection,while a considerable number of high-energy electrons are present in the thin and elongated electron current layer in the OB case.The study provides new insights into magnetic reconnection evolution and the role of boundary conditions in affecting the temporal and spatial distribution of energetic electrons.
Acknowledgments
We acknowledge the support from the Key Research Program of the Chinese Academy of Sciences (No.ZDBSSSW-TLC00105),the National Key R&D Program of China(No.2022YFF0503200),National Natural Science Foundation of China (Nos.41974173 and 42274224),and the Youth Innovation Promotion Association,Chinese Academy of Sciences (No.2019066).
 Plasma Science and Technology2024年4期
Plasma Science and Technology2024年4期
- Plasma Science and Technology的其它文章
- Experimental results of a magnetic field modification to the radio frequency driver of a negative ion source
- A fringe jump counting method for the phase measurement in the HCN laser interferometer on EAST and its FPGA-based implementation
- Simulation of liquid cone formation on the tip apex of indium field emission electric propulsion thrusters
- Novel method for identifying the stages of discharge underwater based on impedance change characteristic
- Performance of pulsed plasma thruster at low discharge energy
- Dynamic propagation velocity of a positive streamer in a 3 m air gap under lightning impulse voltage
