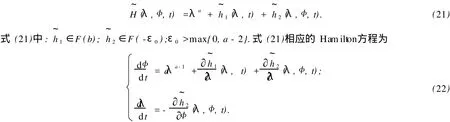平面非自治 Hamilton方程的 Lagrange穩(wěn)定性*
金慧萍
(義烏工商職業(yè)技術學院,浙江義烏 322000)
0 引 言
20世紀 60年代早期,英國著名數(shù)學家 Littlewood[1]研究了平面非自治 Hamilton方程

是否具有 Lagrange穩(wěn)定性,即方程的每個解 x(t)是否都在 t∈(-∞,+∞)上存在,且
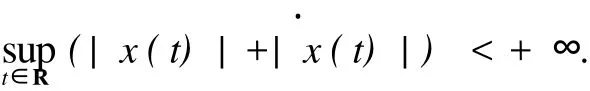
后來,把這一問題稱為 Littlewood有界性問題,且所考慮的方程也更一般,為

關于 Littlewood有界性問題的第 1個正面結果是Morris[2]在研究方程
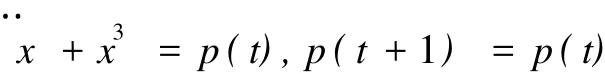
時得到的.接著,Dieckerhoff和 Zehnder[3]把Morris的結果推廣到如下多項式系統(tǒng):

式 (3)中:0≤l≤2n;pj(t)(j=0,1,…,l)為充分光滑的周期為 1的函數(shù).在這一問題上,人們又得到了一系列結果[4-12].
證明周期Hamilton方程具有Lagrange穩(wěn)定性的大致想法如下:設D={(x,x·)∈R2:x2+x·2≤r2}為相平面(x,x·)上一個充分大的圓盤;在R2D上尋找恰當?shù)男磷儞Q,將原系統(tǒng)變?yōu)橐粋€近可積Hamilton系統(tǒng),此時相應的 Poincare映射接近于扭轉映射;由Moser扭轉定理可得該 Poincare映射在距離相平面(x,x·)的原點任意遠處存在不變曲線,它微分同胚于圓環(huán)且圍繞原點;每個這樣的不變曲線對應于原系統(tǒng)的一個在擴展相空間(x,x·,t)∈R2×R上的周期不變柱面;由初值問題的解的存在唯一性,方程的任一解就被限制在這些周期不變柱面之間.
本文將研究多項式系統(tǒng)
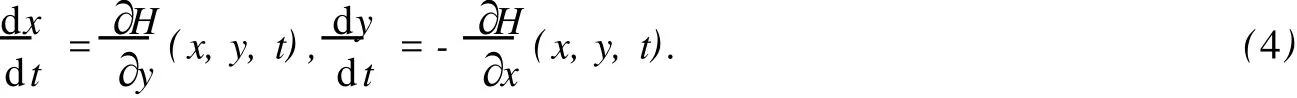
其中

式 (5)中:m,n∈N;I為 (N∪{0})2的有限子集;pi,j∈C∞(t).筆者將證明如下結果:
定理 1 設在系統(tǒng) (4)和系統(tǒng) (5)中,若所有 (i,j)∈I滿足 ni+m j<2m n,則系統(tǒng) (4)的每個解都在(-∞,∞)上存在且有界.
注 1 顯然,當 n=1,j=0且 i<2m時,式 (4)就是式 (3).
注 2 類似于文獻[9],如果將 pi,j對 t的光滑性減弱為 C2,則仍能得到定理 1.
以下總用字母 C表示某些大于 0的常數(shù).
1 辛變換
考慮未擾動系統(tǒng)
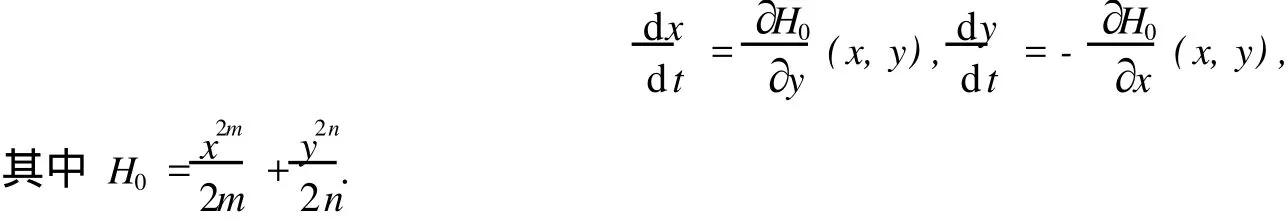
設 (C(t),S(t))為該方程的滿足初始條件 (x(0),y(0))=(0,1)的唯一解,其周期為 T*,則
(1)nC(t)2m+mS(t)2n=m;
(2)C′(t)=S2n-1(t),S′(t)=-C2m-1(t),且 C(0)=0,S(0)=1;
(3)C(t+T*)=C(t),S(t+T*)=S(t).
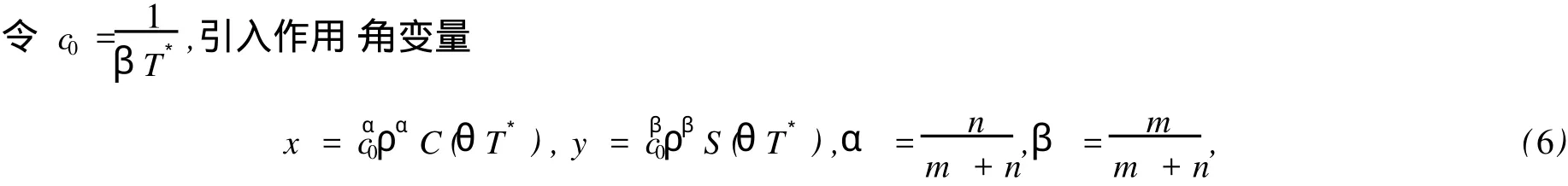
容易驗證式 (6)是一個辛變換.變換 (6)將系統(tǒng) (4)與系統(tǒng) (5)變?yōu)?/p>
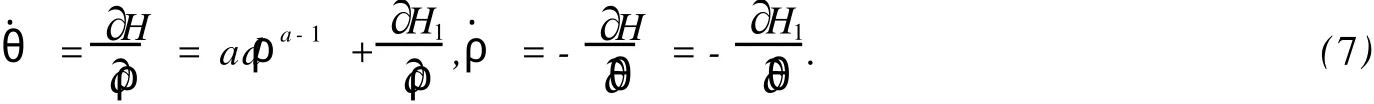
其中
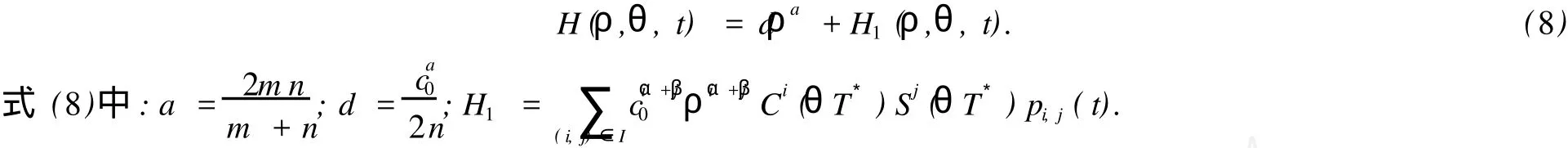
以下將忽略非零常數(shù) d,因為忽略 d不會影響定理 1的證明.
設ρ∈R,(θ,t)∈T2,稱函數(shù) f(ρ,θ,t)∈F(r),如果 f∈C∞且對任意的 i,j,k∈N∪{0},存在 ρijk>0,使得
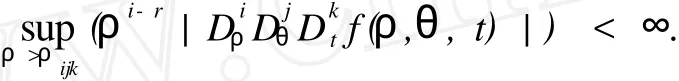
容易證明 F(r)有如下性質:
(1)若 r1 (2)若f∈F(r),則Diρf∈F(r-i),Djθf∈F(r); (3)若 f1∈F(r1),f2∈F(r2),則 f1·f2∈F(r1+r2); 和平環(huán) 性質 1 考慮 Hamilton函數(shù) 其中 h1∈F(c),h2∈F(b),且 a>max{1,c,b},則存在一個周期為 t的辛變換 式 (10)中:U∈F(b-(a-1));V∈F(b-a);Aλ+?Φ (Aλ0)? Aλ-(1?λ-<λ0<λ+),且變換后新的Hamilton函數(shù)形如 先尋找恰當?shù)纳珊瘮?shù)來構造所需的變換Φ.設Φ隱式定義為 以下在函數(shù)中隱去變量 t,并記 h0(ρ)=ρa+h1(ρ,t).在變換Φ的作用下,式 (9)變?yōu)?/p> 其中 設 即 則 引理 1 設 S由式 (13)和式 (14)定義,則由式 (12)定義的辛變換Φ關于 t是周期的,形如 且對充分大的λ滿足U∈F(b-(a-1)),V∈F(b-a). 在變換Φ的作用下,式 (15)變?yōu)?/p> 式(18)中: 引理 2 函數(shù) R1,R2和 R3滿足 多次應用性質 1可以得到性質 2. 性質 2 存在常數(shù)ε0>max{0,a-2}及周期為 t的正則變換Φ =Φj°Φj-1°… °Φ1,使得對 1?λ-<λ0<λ+,有 Aλ+?Φ (Aλ0)? Aλ-,且在Φ的作用下,式 (8)變?yōu)?/p> 這就是為什么需要ε0>a-2的原因 (見引理 3).文獻 [3]所考慮的是 n=1的情形,此時 a-2<0,所以相應的ε0只需大于 0即可.而本文所考慮的一般情形中,n可以是任意自然數(shù),從而相應的 a-2也可以任意大. 接下來將運用Moser扭轉定理證明定理 1.將性質 2應用于式 (8),得 下面估計 f和 g.由于 a可以任意大,所以本文中的 f和 g與文獻[3]中的估計有所不同.利用不等式ε0>max{0,a-2}可以得到引理 3. 引理 3 對任意 i,j∈N∪{0},有 式 (25)和式 (26)兩邊對λ求偏導,得到 于是,也證明了 i=1,j=0的情形.同樣地,式 (25)和式 (26)兩邊對 φ求偏導,得到 因而,對情形 i=0,j=1同樣成立.其他情形可類似證得,故略.引理 3證畢. 作變換 r=r(λ),得到一個新映射 從而,當 t=0時,式 (23)從這條不變曲線出發(fā)的解決定了一個在擴展相空間 (r,φ,t)∈Ar0×R中的不變周期柱面.由初值問題的解的存在唯一性定理知,初值位于這些不變周期柱面內部的解永遠被限制在其內部.從而定理 1得證. [1]Littlewood J.Unbounded solutions ofy"+g(y)=p(t)[J].J LondonMath Soc,1966,41(1):491-496. [2]Morris G.A case of boundedness in littlewood′s problem on oscillatory differenial equations[J].BullAustralMath Soc,1976,14(1):71-93. [3]Dieckerhoff R,Zehnder E.Boundedness of solutions via the twist theorem[J].Ann Scuola Norm Sup Pisa,1987,14(1):79-95. [4]Jin Huiping,WeiBaoshe.OnLittlewood′sproblem for a classof nonpolynomialpotentials[J].南京大學學報:數(shù)學半年刊,2008,25(2):178-189. [5]LeviM.Quasi-periodic motions in superquadratic periodic potentials[J].Comm Math Phys,1991,143(1):43-83. [6]LeviM.KAM theory for particles in periodic potentials[J].Ergod Th&Dynam Sys,1990,10(4):777-785. [7]Liu Bin.Boundedness for solutions of nonlinear Hill′s equations with periodic forcing terms via Moser′s twist theorem[J].Differential Equations,1989,79(2):304-315. [8]Liu Bin.Boundedness of solutions of nonlinear periodic differential equations via Moser′s twist theorem[J].Acta Mathematica Sinca New Series,1992,8(1):91-98. [9]Wang Yiqian,You Jiangong.Boundedness of solutions in polynomial potentialswithC2coefficients[J].ZAMP,1996,47(6):943-952. [10]You Jiangong.Boundedness of solutions of super-linearDuffing′s equations[J].Scientia Sinica,1991,8:805-817. [11]Yuan Xiaoping.Invariant torus ofDuffing equation[D].北京:北京大學,1995. [12]Yuan Xiaoping.Boundedness of solutions ofDuffing-type Equation[J].Science in China,1998,41(6):595-605.
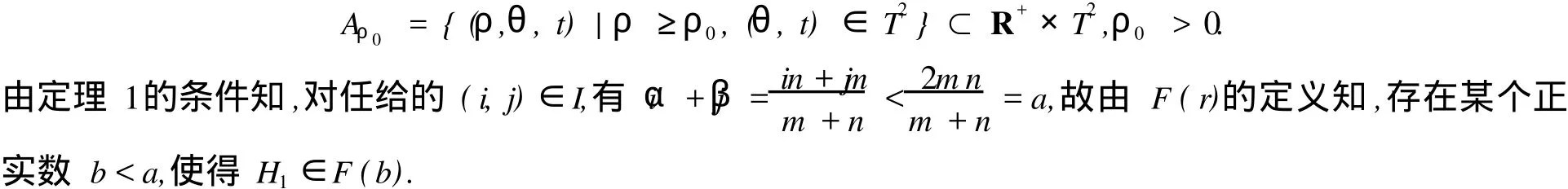

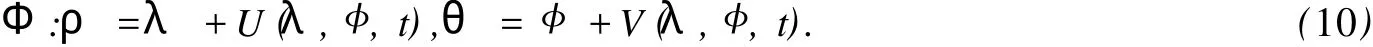
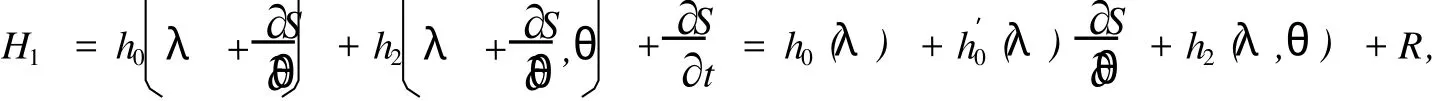
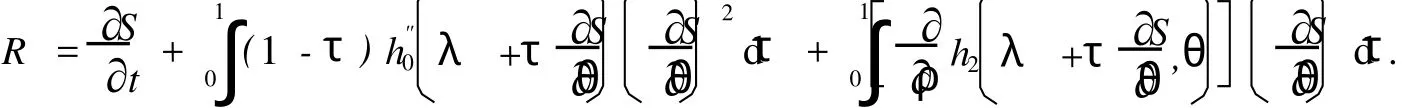





2 定理 1的證明