晏 江,萬(wàn)建武,余 龍

廣州大學(xué),廣東廣州510006

焊球點(diǎn)不同分布模式下的焊球數(shù)量的解析模型研究

晏 江,萬(wàn)建武,余 龍

廣州大學(xué),廣東廣州510006

在數(shù)據(jù)統(tǒng)計(jì)的基礎(chǔ)上,對(duì)倒裝芯片焊球采用叉排布置時(shí),焊球數(shù)量的變化情況進(jìn)行了分析研究,提出了相應(yīng)的解析分析模型,并對(duì)所提出的解析分析模型的可靠性進(jìn)行了驗(yàn)證.研究結(jié)果表明,所得出的解析方程式的計(jì)算結(jié)果與實(shí)際數(shù)據(jù)能很好地吻合.

倒裝芯片;焊球順排;焊球叉排;解析模型

在倒裝芯片的封裝方式中,焊球點(diǎn)是連接芯片和基板的通道.相同尺寸芯片上布置的焊球點(diǎn)越多,意味著芯片具有更高的信號(hào)輸出輸入能力.當(dāng)前焊球的分布模式主要采用順排排列方式,為了在一定程度上增加芯片的輸入輸出(I/O)容量,叉排排列方式在一定條件下是一種可行的焊球分布模式.目前,在這兩種排列方式下,焊球點(diǎn)的數(shù)量變化情況尚處于數(shù)據(jù)統(tǒng)計(jì)及一些簡(jiǎn)單的計(jì)算階段,缺乏理論方面的分析.本文在數(shù)據(jù)統(tǒng)計(jì)的基礎(chǔ)上,對(duì)焊球點(diǎn)的數(shù)據(jù)統(tǒng)計(jì)做出詳細(xì)的解析分析,提出了相應(yīng)的解析分析模型.

1 焊球分布的數(shù)據(jù)統(tǒng)計(jì)

在芯片面積和相鄰焊球點(diǎn)中心距離相同的情況下,如果叉排布置的焊球點(diǎn)比順排的多,這說(shuō)明在芯片面積相同的情況下,焊球點(diǎn)采用叉排布置芯片會(huì)有更高的信號(hào)輸出輸入能力.本文在參考文獻(xiàn)[4]的工作基礎(chǔ)上,取兩種不同的焊球布置情況進(jìn)行分析,相關(guān)統(tǒng)計(jì)數(shù)據(jù)分別列于表1和表2.表1的焊球直徑為168μm,焊球間中心距離為262μm.當(dāng)焊球點(diǎn)為順排方式時(shí),芯片邊緣與焊球點(diǎn)邊緣之間的縫隙寬度為0.122 mm,叉排時(shí)右邊芯片邊緣與焊球點(diǎn)邊緣之間的縫隙寬度不小于0.122 mm.表2的焊球直徑為100μm,焊球間中心距離為250μm.當(dāng)焊球點(diǎn)為順排方式時(shí),芯片邊緣與焊球點(diǎn)邊緣之間的縫隙寬度為0.075 mm,叉排時(shí)右邊芯片邊緣與焊球點(diǎn)邊緣之間的縫隙寬度不小于0.075mm.

表1 直徑為168μm焊球不同布置的統(tǒng)計(jì)結(jié)果Table 1 Statistical results of solder bump of 168μm in diameter under different distribution patterns

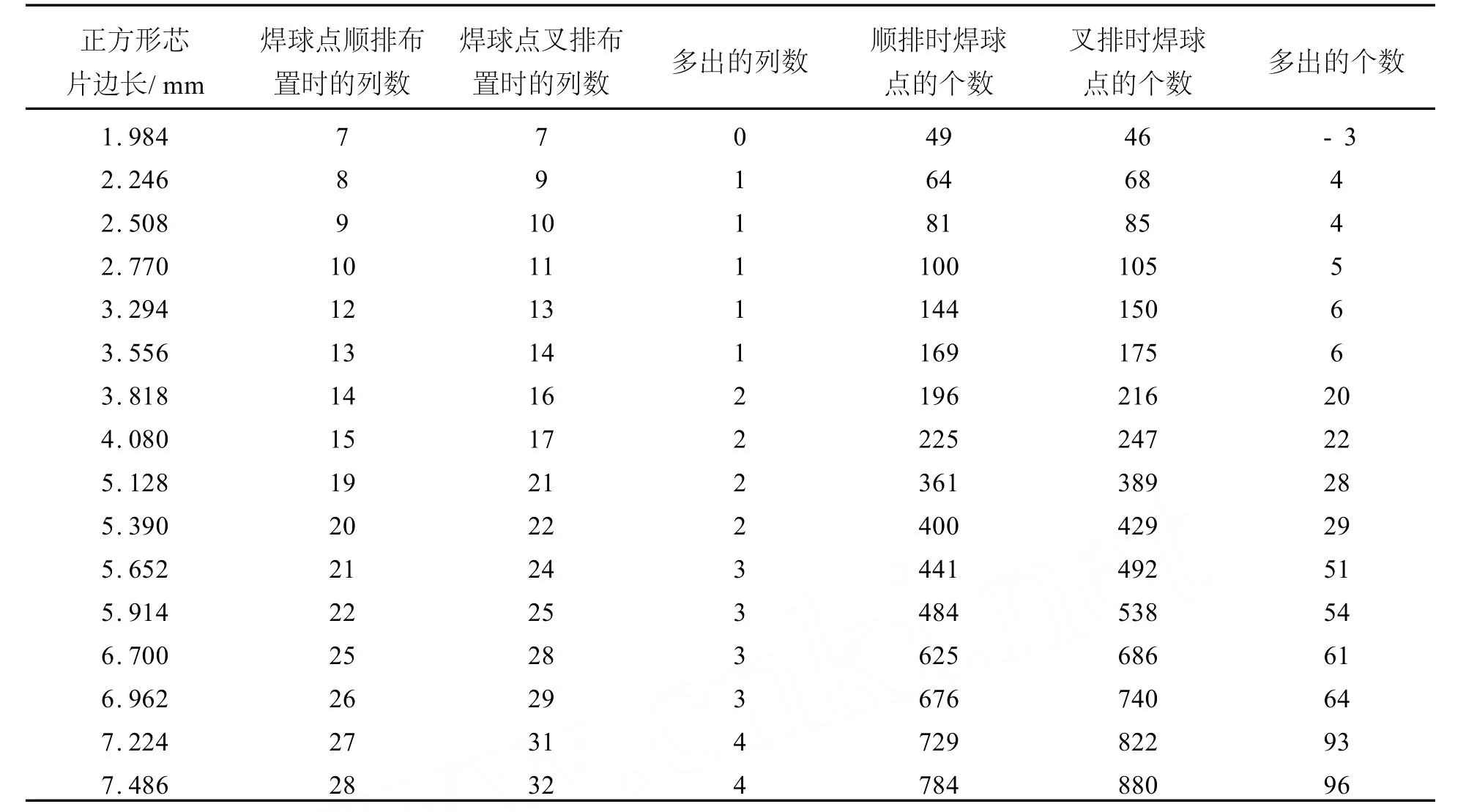
(續(xù)表1)

表2 直徑為100μm焊球不同布置的統(tǒng)計(jì)結(jié)果Table 2 Statistical results of solder bump of 100μm in diameter under different distribution patterns

從表1和表2的統(tǒng)計(jì)數(shù)據(jù)可以看出:隨著芯片面積的不斷變大,采用焊球點(diǎn)叉排布置方式,確實(shí)能夠布置更多的焊球點(diǎn),這樣能提高芯片的信息輸入輸出能力;焊球點(diǎn)的增多與叉排布置時(shí)列數(shù)的變化有著密切的關(guān)系,而且列數(shù)的增加具有一定的規(guī)律.由此可知,在數(shù)據(jù)統(tǒng)計(jì)的基礎(chǔ)上,做出相應(yīng)的解析分析是很有必要的.

2 焊球叉排布置方式的解析分析

2.1 叉排排數(shù)變化的解析分析

為了方便計(jì)算,特將叉排布置中的焊球數(shù)量比相鄰列較少的焊球列向上平移至與第一行對(duì)齊,即將圖1(b)中的第2和4列向上平移個(gè)單位 ,使之變成圖1(c).當(dāng)焊球叉排布置時(shí),與順排相比行列均發(fā)生了變化,但焊球的布置情況又不能同時(shí)滿足各行各列焊球布置的飽滿度.經(jīng)過(guò)圖1(c)的變換后可以做出如此假設(shè),即當(dāng)焊球叉排布置時(shí),焊球的行數(shù)沒(méi)有發(fā)生變化,即和焊球順排布置時(shí)的行數(shù)是一樣的,僅僅是焊球的列數(shù)發(fā)生了變化,并且根據(jù)以上的假設(shè)滿足排數(shù) m1=m2和邊長(zhǎng) l1=l2.從圖1(c)可見(jiàn),經(jīng)變化后的焊球排列的行數(shù)和行距沒(méi)有發(fā)生變化,只是第2列和第4列的焊球比其他列的焊球少一個(gè),即偶數(shù)列的焊球要比奇數(shù)列的焊球少一個(gè).

以下各式中所涉及到的字母為圖1中相對(duì)應(yīng)的參數(shù),其中1代表順排布置,2代表叉排布置;c表示順排布置時(shí),行列方向的邊緣縫隙,同時(shí)也表示叉排布置時(shí)除右邊邊緣外的其他邊緣的邊緣縫隙;c2表示叉排布置時(shí),芯片右邊邊緣的邊緣縫隙.

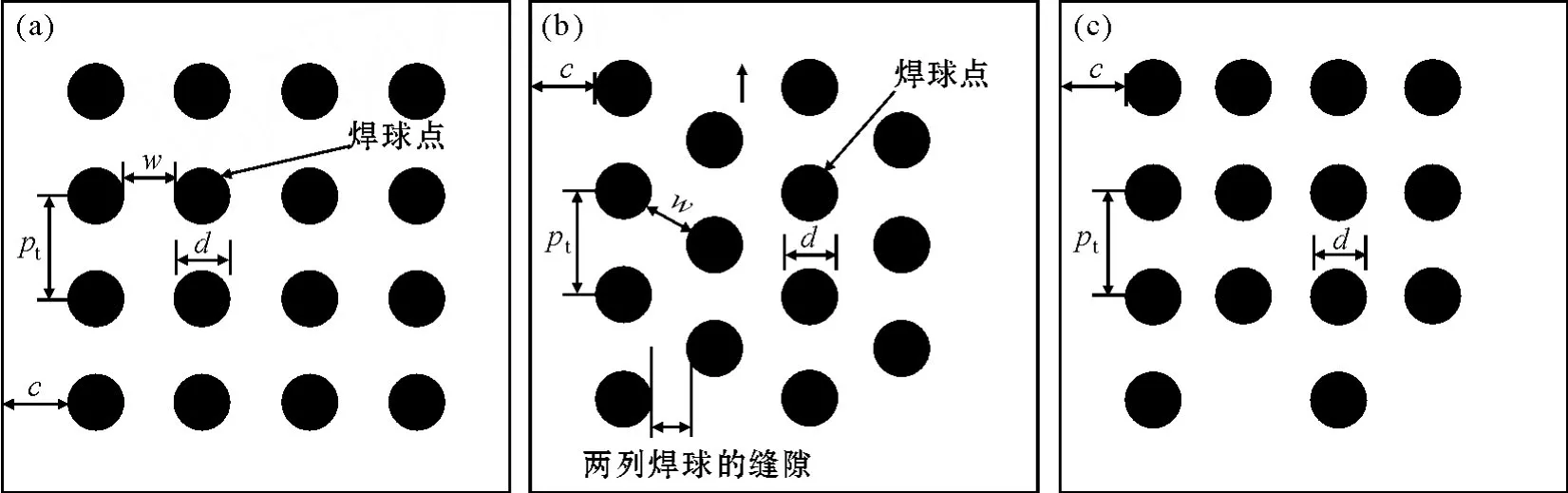
圖1 焊球布置參數(shù)(a)順排布置;(b)叉排布置;(c)變換后的布置Fig.1 Parameters of solder bumps arrangement(a)tandem arrangement;(b)stagger arrangement;(c)arrangement after transfo rm

由于芯片是正方形芯片,在進(jìn)行排列布置焊球時(shí),是按照順排布置模式進(jìn)行比較的,也就是說(shuō),叉排布置時(shí)焊球的行數(shù)是一定的,其長(zhǎng)度即為芯片的邊長(zhǎng).經(jīng)計(jì)算可得:

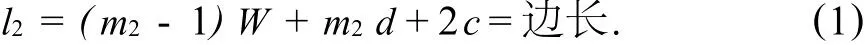
列方向上的計(jì)算方式,與行方向上的計(jì)算稍有區(qū)別,但是芯片是固定的,所以其計(jì)算出的結(jié)果不變,表達(dá)式為:

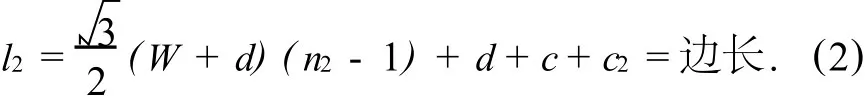
在叉排布置中相鄰兩焊球是以等邊三角形的模式布置的,故相鄰兩焊球的水平間距d),即圖1(c)中的相鄰兩列的中心距為比順排排列(圖1(a))時(shí)焊球的間距縮短,縮短的長(zhǎng)度為:

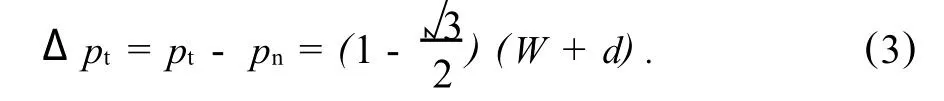
由于焊球間水平距離的縮短,隨著列數(shù)增加到一定的程度,以及Δpt的不斷累積,叉排排列的列數(shù)會(huì)比順排的增多.為使叉排布置時(shí)的焊球列數(shù)增加1列,所需的順排布置的列數(shù)為 n1,則有:

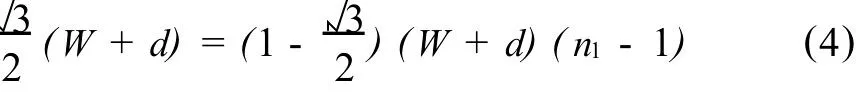
其中n1-1表示相鄰兩列焊球的中心距數(shù),經(jīng)計(jì)算得出n1-1=2+3≈6.646,由此所得出 n1至少為7.464,故 n1的最小值應(yīng)取8,而此時(shí)叉排布置的列數(shù)比順排布置時(shí)的列數(shù)增加了1列.當(dāng)芯片的長(zhǎng)度大于或等于 l1=7(W+d)+2c+d時(shí),可使叉排布置時(shí)的焊球列數(shù)增加,從而增加焊球布置的數(shù)量,提高芯片的輸入輸出容量.

同理,若想叉排布置的列數(shù)比同樣情況下的順排布置的列數(shù)增加 a列,則有:

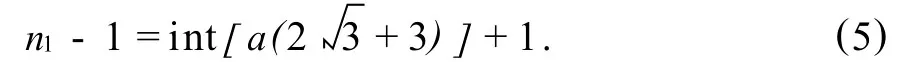
式(5)中int為取整函數(shù).此時(shí)焊球叉排布置時(shí)的列數(shù)比順排布置時(shí)多出 a列,通過(guò)式(4)計(jì)算出的 a與a+1順排的列數(shù)值用 na和na+1表示,則順排布置時(shí)介于這兩個(gè)值之間的任何順排的列數(shù)值,都能夠使同種情況下叉排布置時(shí)的列數(shù)多出a列.

2.2 焊球點(diǎn)數(shù)量變化的解析分析

在計(jì)算叉排布置的焊球的數(shù)量時(shí),已知排列的列數(shù)為 n2,則排數(shù)為 m2的計(jì)算公式如下:

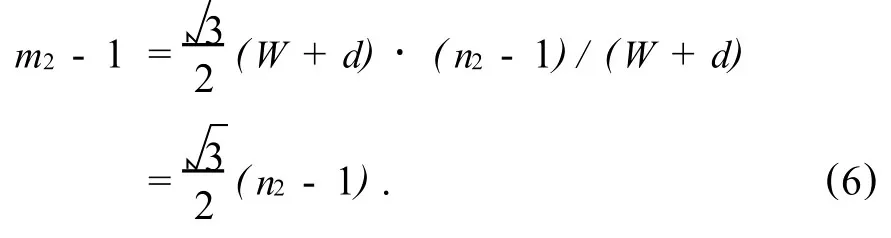
由于芯片是正方形芯片,在進(jìn)行排列布置焊球的時(shí)候,是按照順排布置模式進(jìn)行比較的,也就是說(shuō),叉排布置時(shí)焊球的行數(shù)是一定的,其長(zhǎng)度 l2,即為順排布置時(shí)芯片的邊長(zhǎng),與列數(shù)方向的式(2)進(jìn)行比較,則有c=c2,顯然這個(gè)結(jié)論是不成立的.因?yàn)樯婕暗竭@個(gè)無(wú)限不循環(huán)小數(shù),在滿足行數(shù)方向正常排列的情況下,列數(shù)方向是不可能恰好布置的,此時(shí)的c2應(yīng)該略大于c,但又不能滿足足夠的空間使焊球列數(shù)增加,所以由式(6)可知,當(dāng) m2-1取整時(shí),應(yīng)該取比(n-1)大的最小整數(shù),所以有:2

若已知順排布置情況下的焊球的排數(shù),可以推導(dǎo)出相對(duì)應(yīng)叉排布置時(shí)焊球布置的列數(shù),即:

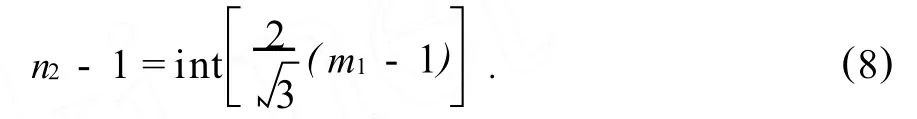
順排布置時(shí),焊球的數(shù)量:

叉排布置時(shí),焊球的數(shù)量為奇數(shù)和偶數(shù)時(shí),方程式分別為:

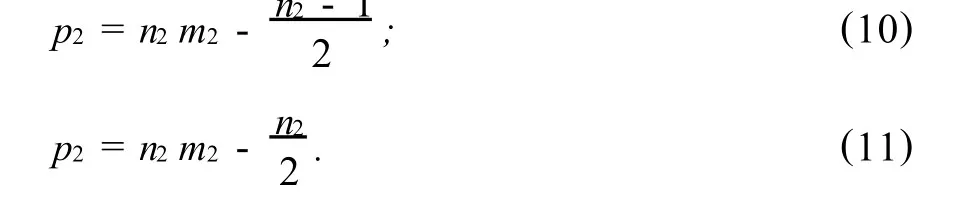
3 解析分析模型的驗(yàn)證

表3為解析分析模型的計(jì)算結(jié)果與表2中有關(guān)數(shù)據(jù)的比較.表3可知,所提出的解析分析模型的計(jì)算結(jié)果與實(shí)際的結(jié)果相符合.表明,解析分析模型是可靠的.

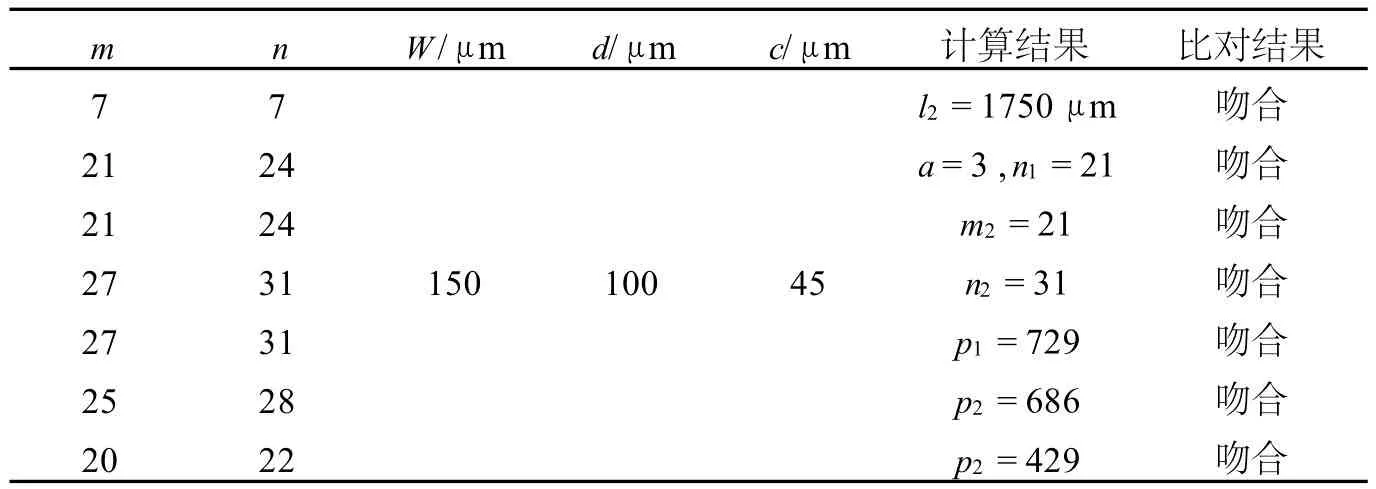
表3 數(shù)據(jù)結(jié)果比對(duì)Table 3 Comparison of data results

4 結(jié) 論

所提出的解析方程式的計(jì)算結(jié)果與實(shí)際數(shù)據(jù)能很好地吻合,在順排和叉排布置情況下,能方便地計(jì)算出焊球的數(shù)量及列數(shù),從而確定哪種方式下焊球的數(shù)量較多,為芯片提供更大的數(shù)據(jù)輸入輸出能力.

[1]譙凱.M EMS器件倒裝芯片封裝中的柔性化凸點(diǎn)制備技術(shù)及其應(yīng)用[D].武漢:華中科技大學(xué),2001.

[2]WAN JW,ZHANGW J,BERGSTROM D.An analyticalmodel fo r p redicting the underfill flow characteristics in flip-chip encapsulation[J].IEEE Transactions on Advanced Packaging,2005,28(2):481-487.

[3]萬(wàn)建武.倒裝芯片封裝的下填充流動(dòng)研究[M].北京:科學(xué)出版社,2008:103-106.

[4]張良明,萬(wàn)建武.焊球分布模式對(duì)芯片下填充膠流動(dòng)的影響[J].電子工藝技術(shù),2008,29:3.

Study on analyticalmodel of solder-bump number under different distribution patterns

YAN Jiang,WAN Jianw u,YU Long
Guangzhou University,Guangzhou 510006,China

In this paper,on the basisof statistical data,through the analysisof solder-bump number in staggered arrangement of flip-chip package,an analyticalmodel is p roposed,and the reliability of the model is also validated in thispaper.The results show that the analytical equation can bewell in agreementw ith the actual data.

flip-chip;aligned arrangement;staggered arrangement;analyticalmodel

TF123.121

A

1673-9981(2011)02-0125-05

2010-11-22

晏江(1986—),男,湖北應(yīng)城人,碩士研究生.