劉合國,王麗

(湖北大學(xué)數(shù)學(xué)與計算機(jī)科學(xué)學(xué)院,湖北 武漢 430062)

(i)當(dāng)m=1時,Aut(HolG)?1;

(ii)當(dāng)m=2時,Aut(HolG)?HolG=D8;

(iii)當(dāng)m≥3時,HolG的內(nèi)自同構(gòu)群

Inn(HolG)=〈x,y,z|x2=y2m-2=z2m-1=1,[x,y]=1,zx=z-1,zy=z3〉,

且Aut(HolG)/Inn(HolG)?2×2.

關(guān)鍵詞有限循環(huán)2-群;全形;自同構(gòu)群

中圖分類號O152.3文獻(xiàn)標(biāo)志碼A

文獻(xiàn)[2-5]中已經(jīng)確定了可裂的亞循環(huán)p-群的自同構(gòu)群的結(jié)構(gòu),近來文獻(xiàn)[6]中完全確定了可裂的亞循環(huán)群的自同構(gòu)群的結(jié)構(gòu),這樣當(dāng)p為奇素數(shù)時,循環(huán)p-群G的全形HolG的自同構(gòu)群Aut(HolG)就可以完全確定了.事實(shí)上,當(dāng)G?pm時,由文獻(xiàn)[6]中引理3.2知

Holpm?(pm-1pm)×p-1,

最后由文獻(xiàn)[6]中定理4.6可以得 Aut(Holpm)?(p-1Sp)×Autp-1,

現(xiàn)在我們要確定有限循環(huán)2-群全形的自同構(gòu)群的結(jié)構(gòu).

引理當(dāng)m≥3,k≥0時,下述結(jié)論成立.

(i) 32k+1≡1(mod 2),但32k+1?1(mod 22);

(ii)32k+1≡-1(mod 22),但32k+1?-1(mod 23);

(iii)32k≡-1(mod 2),但32k?-1(mod 22);

(iv)32m-2(2k+1)≡1(mod 2m),但32m-2(2k+1)?1(mod 2m+1).

引理的證明(i),(ii),(iii)式容易驗證,只對(iv)進(jìn)行證明.

當(dāng)m=3時,32m-2(2k+1)-1=32(2k+1)-1=(32k+1-1)(32k+1+1),由(i),(ii)知

32(2k+1)≡1(mod 23),32(2k+1)?1(mod 24).

歸納地假設(shè)

32m-2(2k+1)≡1(mod 2m),32m-2(2k+1)?1(mod 2m+1).

因為

32m-1(2k+1)-1=(32m-2(2k+1))2-1=(32m-2(2k+1)-1)(32m-2(2k+1)+1),

所以

32m-1(2k+1)≡1(mod 2m+1),32m-1(2k+1)?1(mod 2m+2),

證畢.

當(dāng)G?2時,Aut(HolG)?1;當(dāng)G?22時,G的全形HolG是8階二面體群,此時Aut(HolG)?HolG=D8.

當(dāng)G?2m,m≥3時,令G=〈z〉?2m,G有兩個典型的自同構(gòu)x和y：

x:G→G,z|→z-1;

y:G→G,z|→z3.

其中|x|=2,|y|=2m-2.因為Aut2m?2×2m-2,所以AutG?〈x〉×〈y〉.這樣

[xaybzc,x]=z-2c,

[xaybzc,y]=z2c,

[xaybzc,z]=z1-(-1)a3b,

得c≡0(mod 2m-1),且(-1)a3b≡1(mod 2m),根據(jù)引理得a=0,b=0,c=0或者2m-1.所以ζH?〈z2m-1〉,又因〈z2m-1〉?ζH,故ζH=〈z2m-1〉.

一方面由[x,z]=z2可得z2∈H′,故〈z2〉≤H′;另一方面由〈z2〉char〈z〉H可得〈z2〉H,又由[x,z]=z2,[z,y]=z2知H/〈z2〉是Able群,于是有H′≤〈z2〉,從而H′=〈z2〉.因H是有限2-群,故FratH=H′H2,其中H2=〈h2|h∈H〉,所以便有FratH=〈y2,z2〉.

任取ψ∈AutH,設(shè)

ψ:H→H

x|→xa11ya21za31y2b11z2b21,

y|→xa12ya22za32y2b12z2b22,

z|→xa13ya23za33y2b13z2b23.

其中aij=0或者1;0≤2b1j<2m-2,0≤2b2j<2m(i,j=1,2,3).

(i)當(dāng)m=3時,|AutH|=26,ψ具有如下形式:

ψ:H→H,x|→xz2i,y|→yz2k,z|→22j+1

或者

ψ:H→H,x|→yz2i,y|→xz2k,z|→xyz2j+1,

其中2|(k+i);

(ii)當(dāng)m≥4時,|AutH|=22m,ψ具有如下形式:

ψ:H→H,x|→xz2i,y|→yz2k,z|→z2j+1

或者

ψ:H→H,x|→xy2m-3z2i,y|→y2m-3+1z2k,z|→zy2m-3z2j,

其中2m-2|(k+i).

(xa11ya21za31y2b11z2b21)2= (xa11ya21+2b11z32b11a31+2b21)2=x2a11y2a21+4b11z(32b11a31+2b21)[1+(-1)a113a21+2b11]=

y2a21+4b11z(32b11a31+2b21)[1+(-1)a113a21+2b11].

所以有

2a21+4b11≡0(mod 2m-2),

而且

(32b11a31+2b21)[1+(-1)a113a21+2b11]≡0(mod 2m).

根據(jù)引理可得當(dāng)m≥4時,

(i)a11=0,a21=0,a31=0,2b11=0,2b21=2m-1,此時2階元形如z2m-1;

(ii)a11=0,a21=0,a31=0,2b11=2m-3,2b21=0,此時2階元形如y2m-3;

(iii)a11=0,a21=0,a31=0,2b11=2m-3,2b21=2m-1,此時2階元形如y2m-3z2m-1;

(iv)a11=1,a21=0,a31=0,2b11=0,2b21=2i,此時2階元形如xz2i;

(v)a11=1,a21=0,a31=1,2b11=0,2b21=2i,此時2階元形如xz2i+1;

(vi)a11=1,a21=0,a31=0,2b11=2m-3,2b21=2i,此時2階元形如xy2m-3z2i.

當(dāng)m≥4時,由數(shù)學(xué)歸納法得

(xa12ya22za32y2b12z2b22)2m-2= (xa12ya22+2b12z32b12a32+2b22)2m-2=

y2m-2(a22+2b12)zez=zez,

其中ez=(32b12a32+2b22)[1+(-1)a123a22+2b12+…+(-1)(2m-2-1)a123(2m-2-1)(a22+2b12)].

于是當(dāng)(-1)a123a22+2b12=1時

ez=(32b12a32+2b22)2m-2,(xa12ya22za32y2b12z2b22)2m-2=z(32b12a32+2b22)2m-2.

當(dāng)(-1)a123a22+2b12≠1時,

ez≡0(mod 2m),ez?0(mod 2m+1);

或者

ez≡0(mod 2m),2m-2(a22+2b12)?0(mod 2m-1),

于是當(dāng)(-1)a123a22+2b12=1時,即a12=a22=2b12=0,有

ez=(32b12a32+2b22)2m-2=(a32+2b22)2m-2,

2m-2(a22+2b12)=0≡0(mod 2m-1).

所以

(a32+2b22)2m-2≡0(mod 2m),(a32+2b22)2m-2?0(mod 2m+1).

即

a32+2b22≡0(mod 22),a32+2b22?0(mod 23).

從而a32=0,2b22=22(2j+1),故a12=0,a22=0,a32=0,2b12=0,2b22=22(2j+1),此時2m-2階元形如z22(2j+1).

當(dāng)(-1)a123a22+2b12≠1時,a12,a22,2b12不同時為0.

(i) 若a22=0,則有

2m-2(a22+2b12)=2m-1b12≡0(mod 2m-1).

所以

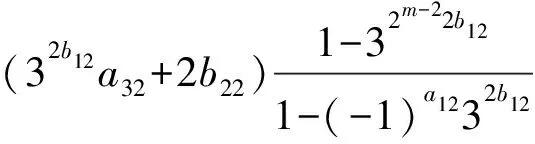
若a12=0,則

因為a12,a22,2b12不同時為0,所以可設(shè)2b12=2t(2k+1)(其中t≥1,k≥0),此時有

于是可得

(32b12a32+2b22)≡0(mod 22),(32b12a32+2b22)?0(mod 23).

由此解得a32=0,2b22=22(2j+1),故a12=0,a22=0,a32=0,2b12=2i(其中i≥1),2b22=22(2j+1),此時2m-2階元形如y2iz22(2j+1)(其中i≥1).

若a12=1,則有

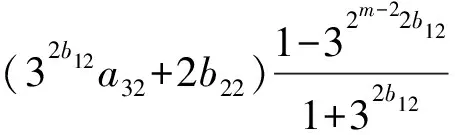
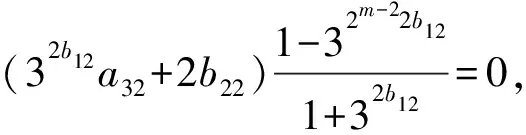
于是可得t=1且(32b12a32+2b22)?0(mod 2).由此解得a32=1,2b12=2(i+1),故a12=1,a22=0,a32=1,2b12=2(2i+1),2b22=2j,此時2m-2階元形如xzy2(2i+1)z2j.

(ii)若a22=1,則有

2m-2(a22+2b12)=2m-2(1+2b12)?0(mod 2m-1).

同上分a12=0和a12=1兩種情況進(jìn)行討論,得形如y2i+1z2j,xy2i+1z22j的元階也是2m-2.

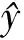
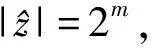
(4)注意到

[xa1yb1zc1,xa2yb2zc2]=zc1((-1)a23b2)-c2((-1)a13b1),

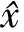
[z2m-1,z2j+1]=1,

[y2m-3z2m-1,z2j+1]=z(2j+1)(1-32m-3),

[xzi,z2j+1]=z2(2j+1),

[xy2m-3z2i,z2j+1]=z(2j+1)(1+32m-3).

[z2m-1,zy2m-3z2j]=1,

[y2m-3,zy2m-3z2j]=z(32m-3+2j)(1-32m-3),

[y2m-3z2m-1,zy2m-3z2j]=z(32m-3+2j)(1-32m-3),

[xzi,zy2m-3z2j]=z2(32m-3+2j)+i(32m-3-1),

[xy2m-3z2i,zy2m-3z2j]=z(32m-3+2j)(1+32m-3).

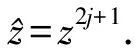
[z4,z2j+1]=1,

[yz2i,z2j+1]=z-2(2j+1),

[xzi,z2j+1]=z2(2j+1),

[xyz4i,z2j+1]=z4(2j+1).

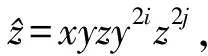
當(dāng)m=3時,

當(dāng)m≥4時,

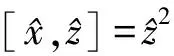
[z2j+1,y2iz22(2k+1)]=z(2j+1)(32i-1),[z2j+1,xzy2(2i+1)z2k]=z-(2j+1)(1+32(2i+1)),

[z2j+1,y2i+1z2k]=z(2j+1)(32i+1-1),[z2j+1,xy2i+1z22k]=z-(2j+1)(1+32i+1).

[zy2m-3z2j,y2iz22(2k+1)]=z(32i-1)(32m-3+2j),

[zy2m-3z2j,xzy2(2i+1)z2k]=z(32(2i+1)+2k)(1-32m-3)z-(32(2i+1)+1)(32m-3+2j),

[zy2m-3z2j,y2i+1z2k]=z(32i+1-1)(32m-3+2j),

[zy2m-3z2j,xy2i+1z22k]=z-(32i+1+1)(32m-3+2j).

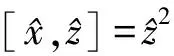
[z2j+1,z4]=1,

[z2j+1,yz2k]=z2(2j+1),

[z2j+1,xzk]=z-2(2j+1),

[z2j+1,xyz4k]=z-4(2j+1).

[xyz2j+1,z4]=1,[xyz2j+1,yz2k]=z2(2j+1),

[xyz2j+1,xzk]=z4kz-2(2j+1),[xyz2j+1,xyz4k]=z-4(2j+1).

當(dāng)m=3時,

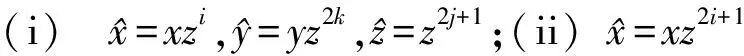
當(dāng)m≥4時,

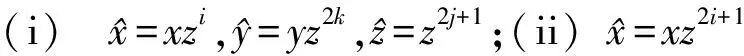
當(dāng)m≥4時,

ψ:H→H,x|→xz2i,y|→yz2k,z|→z2j+1

的自同構(gòu)ψ有22m-1個(其中2m-2|(k+i)).

因為

[xz2i+1,y2m-3+1z2k]=z4kz(2i+1)(3(2m-3+1)-1)≠1,

[xy2m-3z2i,y2m-3+1z2k]=z2k(32m-3+1)z2i[3(2m-3+1)-1].

若

2k(32m-3+1)+2i[3(2m-3+1)-1]≡0(mod 2m),

即

2(32m-3-1)(k+3i)+2(2k+2i)≡0(mod 2m),

2k+2i≡0(mod 2m-1),

ψ:H→H,x|→xy2m-3z2i,y|→y2m-3+1z2k,z|→zy2m-3z2j

的自同構(gòu)ψ有22m-1個(其中2m-2|(k+i)).

當(dāng)m=3時,

同m≥4時的情況,可知滿足ψ:H→Hx|→xz2i,y|→yz2k,z|→z2j+1

的自同構(gòu)ψ有25個(其中2|(k+i)).

因為

[xz2i+1,xz2k]=z2(2k-2i-1)≠1,[yz2i,xz2k]=z-2(2k+2i).

若

-2(2k+2i)≡0(mod 23),

即

2k+2j≡0(mod 22),

故滿足

ψ:H→H,x|→yz2i,y|→xz2k,z|→xyz2j+1

的自同構(gòu)ψ有25個(其中2|(k+i)),證畢.

定理2設(shè)G是2m階循環(huán)群(m≥3),記

H:=HolG=〈x,y,z|x2=y2m-2=z2m=1,[x,y]=1,zx=z-1,zy=z3〉.

則

InnH=〈x,y,z|x2=y2m-2=z2m-1=1,[x,y]=1,zx=z-1,zy=z3〉,

且AutH/InnH?2×2.

定理2的證明已知ζH=〈z2m-1〉.于是可得

InnH?H/ζH=〈x,y,z|x2=y2m-2=z2m-1=1,[x,y]=1,zx=z-1,zy=z3〉.

現(xiàn)將xa11ya21za31y2b11z2b21共軛地作用在生成元x,y,z上時,得到

xxa11ya21za31y2b11z2b21=xz2(32b11a31+2b21);

yxa11ya21za31y2b11z2b21=yz-2(32b11a31+2b21);

zxa11ya21za31y2b11z2b21=z(-1)a113a21+2b11.

因2(32b11a31+2b21)可取遍0,1,2,…,2m-1中所有偶數(shù),(-1)a113a21+2b11可取遍0,1,2,…,2m-1中所有奇數(shù),故xa11ya21za31y2b11z2b21所誘導(dǎo)的內(nèi)自同構(gòu)有2m-12m-1=22m-2個.又因InnH?(2×2m-2)2m-1,故|InnH|=22m-2,于是H的任意內(nèi)自同構(gòu)必定把x映射為把y映射為把z映射為

注意到|AutH|=22m,|InnH|=22m-2,可得|OutH|=|AutH/InnH|=4.

當(dāng)m=3時,取α,β∈AutH,其中

α:H→H,x|→yz2,y|→xz2,z|→xyz.β:H→H,x|→xz4,y|→y,z|→z.

則α,β?InnH,且可以驗證α2=β2=1,即|αInnH|=|βInnH|=2.因為

αβ:H→H,x|→yz6,y|→xz2,z|→xyz.

所以αβ?InnH,αInnH≠βInnH.

于是可得

AutH/InnH=〈αInnH〉×〈βInnH〉?2×2;

當(dāng)m≥4時,取α,β∈AutH,其中

α:H→H,x|→xz2m-1,y|→y,z|→z.β:H→H,x|→xy2m-3z2m-1,y|→y2m-3+1,z|→zy2m-3.

.

同理可以驗證|αInnH|=|βInnH|=2,αInnH≠βInnH.

于是可得

AutH/InnH=〈αInnH〉×〈βInnH〉?2×2,

證畢.

[1] Kargapolov M I, Merzljakov Ju I.Fundamentals of the theory of groups[M].NewYork:Springer-Verlag,1979.

[2] Curran M J.The automorphism group of a split metacyclic 2-group[J].Arch Math,2007,89:10-23.

[3] Bidwell J N,Curran M J. The automorphism group of a split metacyclic p-group[J].Arch Math,2006,87:488-497.

[4] Zhou Fang,Liu Heguo.Automorphism groups of semidirect products[J].Arch Math,2008,91:193-198.

[5] Bidwell J N, Curran M J. Corrigendum to “The automorphism group of a split metacyclic p-group”[J].Arch Math,2009,92:14-18.

[6] Golasiński M, GonCalves D L. On automorphisms of split metacyclic groups[J].Manuscripta Math,2009,128:251-273.