楊文玲,任苗苗,邵勇

(西北大學(xué)大學(xué)數(shù)學(xué)系,陜西西安 710127)

關(guān)于幾類2階ai-半環(huán)生成的簇的研究

楊文玲,任苗苗,邵勇

(西北大學(xué)大學(xué)數(shù)學(xué)系,陜西西安 710127)

借助半環(huán)的格林關(guān)系研究了由所有2階ai-半環(huán)生成的半環(huán)簇S2的一些子簇.

其次,定義了與S2中半環(huán)的元素相關(guān)的同余關(guān)系,并揭示了同余關(guān)系之間的聯(lián)系.

半環(huán);格林關(guān)系;簇;同余

DO I：10.3969/j.issn.1008-5513.2013.05.009

1 引言及預(yù)備知識(shí)

設(shè)(S,+,·)是一個(gè)(2,2)-型代數(shù),其中+和·是S上的二元運(yùn)算.若S滿足下列條件:

(1)(S,+)是交換半群;

(2)(S,·)是半群;

(3)a·(b+c)=a·b+a·c,(a+b)·c=a·c+b·c(?a,b,c∈S).

則稱(S,+,·)是半環(huán).由此可見半環(huán)是環(huán)和分配格的共同推廣.所謂的半格是指交換的冪等元半群.加法半群為半格的半環(huán)簡稱為ai-半環(huán).眾所周知,半格的自同態(tài)半環(huán)是ai-半環(huán),且每一個(gè)ai-半環(huán)可嵌入到某一個(gè)半格的自同態(tài)半環(huán)中[1].設(shè)S是半群.P(S)(Pf(S))表示S的非空(有限)子集的全體.在P(S)上定義+和·如下:

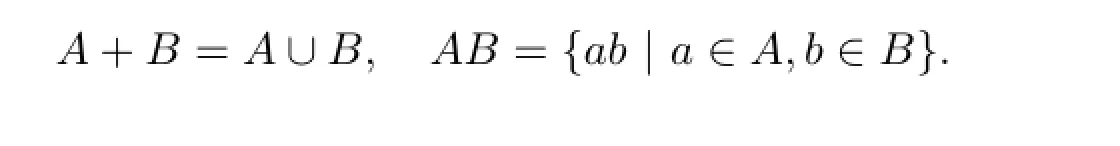
則P(S)和Pf(S)成為ai-半環(huán).事實(shí)上,若X+表示自由半群,則Pf(X+)是所有ai-半環(huán)作成簇的自由對(duì)象[1].

許多學(xué)者對(duì)ai-半環(huán)進(jìn)行了研究[2-7].文獻(xiàn)[7]引入了半群的閉子半群的概念,進(jìn)而給出了所有乘法半群是帶的ai-半環(huán)作成的簇的自由對(duì)象的模型.其后,文獻(xiàn)[2-4]證明了上述簇的子簇格是分配格,且有78個(gè)元素.此外,每一個(gè)子簇都是有限基底的和有限生成的.在上述文獻(xiàn)的基礎(chǔ)上,本文研究所有2階ai-半環(huán)生成的簇.

容易驗(yàn)證,在同構(gòu)意義下有6個(gè)互不相同的2階ai-半環(huán),分別記為L2,R2,M2,D2,N2和T2,其運(yùn)算表如下.

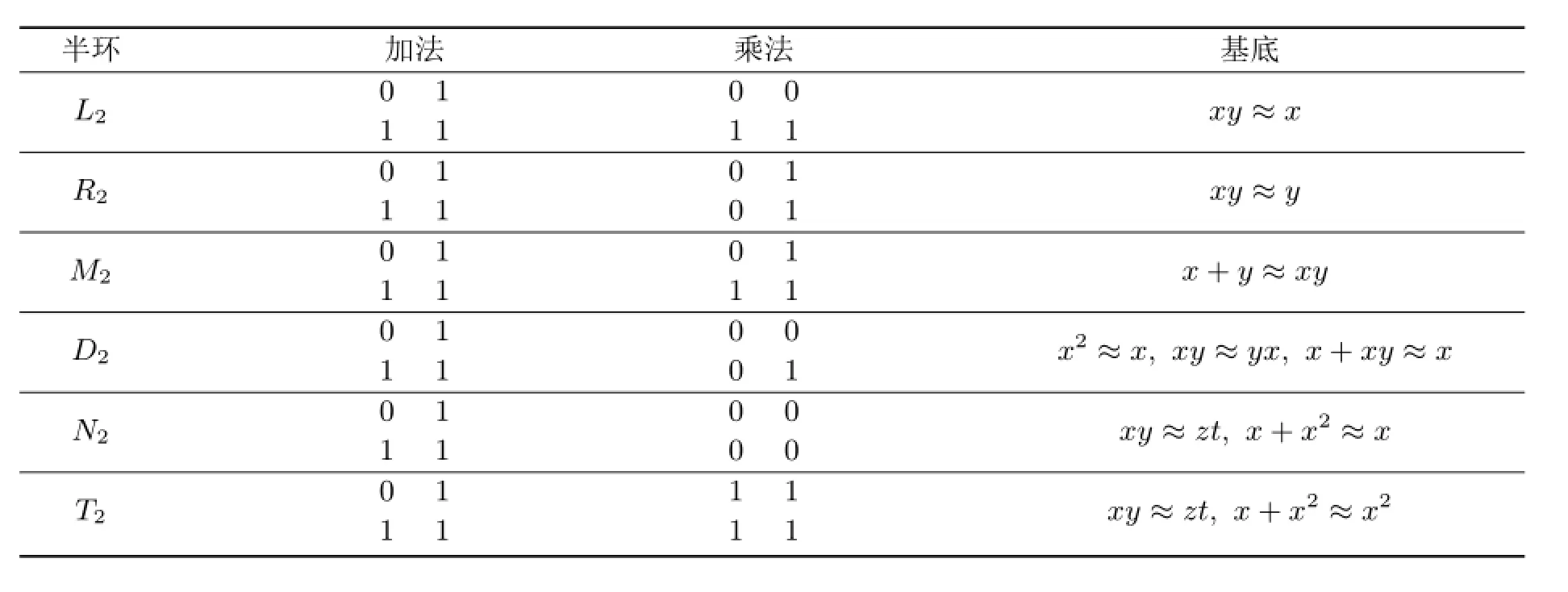
表1 L2,R2,M2,D2,N2和T2運(yùn)算表

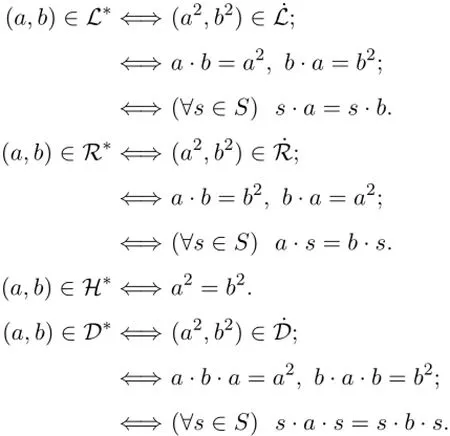
證明得到

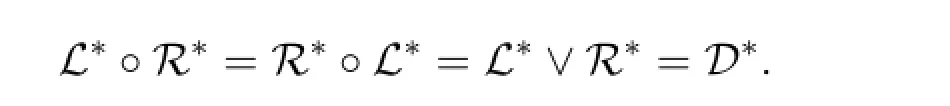
為了應(yīng)用方便起見,下文均用ab表示a·b,Con(S)表示半環(huán)S上所有同余所構(gòu)成的集合.對(duì)于給定的半環(huán)S,HSP(S)表示由半環(huán)S所生成的簇.文中沒有給出的概念和符號(hào)可以參考文獻(xiàn)[8-9].

本文首先利用半環(huán)的格林關(guān)系研究了由所有2階ai-半環(huán)生成的半環(huán)簇S2的一些子簇,給出了這些子簇的基底.其次,定義了與S2中半環(huán)的元素相關(guān)的同余關(guān)系,并對(duì)同余關(guān)系之間的聯(lián)系進(jìn)行了研究.

2 主要內(nèi)容

表2 L2×N2的加法運(yùn)算表

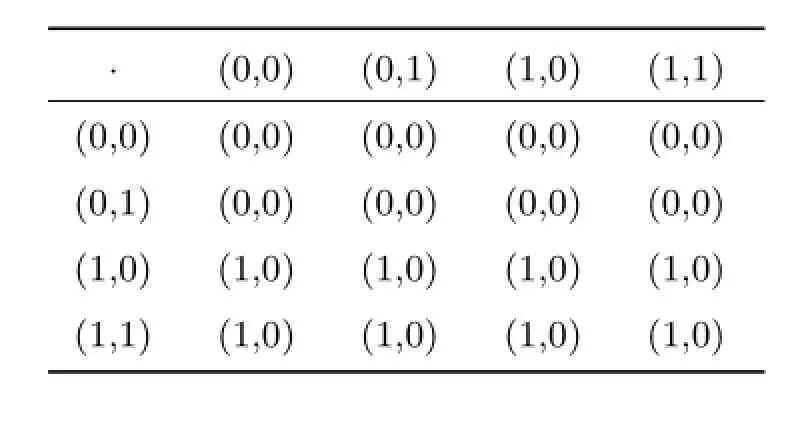
表3 L2×N2的乘法運(yùn)算表

[1]KuˇrilM,Pol′ak L.On varieties of sem ilattice-ordered sem igroup[J].Sem igroup Forum,2005,71(1):27-48.

[2]Pastijin F,Zhao X Z.Varieties of idem poten t sem irings w ith commu tative add ition[J].A lgebra Universalis, 2005,54:301-321.

[3]Ghosh S,Pastijn F,Zhao X Z.Varieties generated by ordered bands I[J].Order,2005,22:109-128.

[4]Pastijn F.Varieties generated by ordered bands II[J].Order,2005,22:129-143.

[5]Zhao X Z,Shum K P,Guo Y Q.L-subvarieties of the variety of idem potent sem irings[J].A lgeb ra Univers, 2001,46:75-96.

[6]Zhao X Z,Guo Y Q,Shum K P.D-subvarietiesof the variety of idem potent sem irings[J].A lgebra Colloquium, 2002,9:15-28.

[7]Zhao X Z.Idem potent sem iringsw ith a comm utative additive reduct[J].Sem igroup Forum,2002,64:289-296.

[8]Burris S,Sankppanaver H P.A Course in Universal A lgebra[M].New York:Sp ringer Verlag,1981.

[9]How ie JM.Fundamentals of Sem igroup Theory[M].Oxford:Oxford Science Pub lication,1995.

[10]Bhuniya A K,M ondal T K.Distribu tive lattice decom positions of sem irings w ith a sem ilattice add itive reduct[J].Sem igroup Forum,2010,80(2):293-301.

The study of som e classes of the varieties generated by ai-sem irings of order tw o

Yang Wenling,Ren M iaom iao,Shao Yong

(Departm ent of M athem atics,Northwest University,X i′an 710127,China)

In this paper,we study som e subvarieties of the variety S2generated by all ai-sem irings of order tw o by Green′s relations of a sem iring.A lso,we defne some congruenceswhich are related to elements of a sem iring in S2and show the relationships of these congruences.

sem iring,Green′s relations,variety,congruence

O153.3

A

1008-5513(2013)05-0498-09

2013-04-10.

陜西省自然科學(xué)專項(xiàng)基金(2011JQ 1017);西北大學(xué)科學(xué)研究基金(NC0925).

楊文玲(1988-),碩士生,研究方向：代數(shù)學(xué).

2010 MSC:16Y60