張志兵,陳撫良

(江西師范大學(xué)數(shù)信學(xué)院,江西南昌 330022)

局部對(duì)稱的黎曼流形中的極小子流形

張志兵,陳撫良

(江西師范大學(xué)數(shù)信學(xué)院,江西南昌 330022)

主要研究了局部對(duì)稱的黎曼流形中的定向緊致無邊極小子流形的內(nèi)蘊(yùn)剛性問題,利用一個(gè)矩陣不等式,得到了這類子流形的一個(gè)剛性定理.所得結(jié)果部分改進(jìn)了已有的一個(gè)結(jié)論.

局部對(duì)稱的黎曼流形;極小子流形;矩陣不等式

1 引言

2 預(yù)備知識(shí)及引理

3 定理的證明

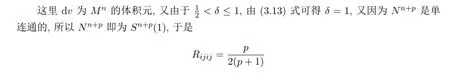
這時(shí)利用定理1.3的情況(2),可得定理1.4的結(jié)論(2),從而定理1.4得證.

致謝非常感謝審稿人的幫助和指正．

[1]Yau S T.Subm anifolds w ith constan tm ean cu rvature II[J].Am er.J.M ath.,1975,97:76-100.

[2]紀(jì)永強(qiáng),徐森林.局部對(duì)稱黎曼流形中的極小子流形[J].東北數(shù)學(xué),2005,21(1):61-69.

[3]Gu J R,Xu H W.On Yau Rigidity Theorem For M inimal Submanifolds In Spheres[J].M ath.Res.Lett., 2012,19(3):211-523.

[4]紀(jì)永強(qiáng).子流形幾何[M].北京:科學(xué)出版社,2004.

[5]Lu Z Q.Normal scalar curvature con jecture and its app lications[J].Journal Functional Analysis,2011,261: 1284-1308.

[6]Ge JQ.Tang Z Z.A p roof of the DDVV con jectu re and its equality case[J].Pacif c J.M ath.,2008,237:87-95.

[7]Lu Z Q.Recent developments of the DDVV con jecture[J].Bull.Transil.Univ.Brasov.Ser.B,2008,14: 133-144.

M inim al subm anifold in locally symm etric R iem ann ian m an ifold

Zhang Zhibing,Chen Fuliang
(Department of M athematics,Jiangxi Normal University,Nanchang 330022,China)

In this paper,wemain ly investigate rigidity p rob lem of the oriented com pactm inimal submanifold in local symm etry Riem annian m anifold,using a m atrix inequality,got a rigid ity theorem of this kind of subm anifold．The resu lts im prove partly a conclusion w hich has been pub lished.

locally symmetric Riemannian manifold,m inimal submanifold,matrix inequality

O 186.12

A

1008-5513(2013)04-0373-09 DO I：10.3969/j.issn.1008-5513.2013.04.007

2013-06-19.

國(guó)家自然科學(xué)基金(11226078,11261038).

張志兵(1987-),碩士,研究方向：微分幾何.

2010 M SC:53C20