張姍姍,瞿萌,束立生

(安徽師范大學(xué)數(shù)學(xué)計算機(jī)科學(xué)學(xué)院,安徽蕪湖 241003)

Bochner-Riesz算子交換子在加權(quán)Morrey空間上的有界性

張姍姍,瞿萌,束立生

(安徽師范大學(xué)數(shù)學(xué)計算機(jī)科學(xué)學(xué)院,安徽蕪湖 241003)

運用了Sharp極大函數(shù)估計的方法證明了當(dāng)權(quán)函數(shù)滿足一定條件時,Bochner-Riesz算子與加權(quán)BMO函數(shù)生成的交換子在加權(quán)Morrey空間上的有界性.

Bochner-Riesz算子;加權(quán)Morrey空間;加權(quán)BMO空間

1 引言及相關(guān)定義

經(jīng)典的Morrey空間Lp,λ首先是由Morrey[1]在研究二階橢圓型偏微分方程解的局部性質(zhì)時所引進(jìn)的.2009年,Komori和Shirai[2]建立了加權(quán)Morrey空間Lp,κ(ω)并且研究了調(diào)和分析中一些主要算子,比如Hardy-Littlewood極大算子,Calder′on-Zygmund奇異積分算子以及分?jǐn)?shù)次積分算子在這些加權(quán)Morrey空間上的有界性問題.在?n(n≥2)中階為δ＞0 的Bochner-Riesz算子起初是通過Fourier變換,對Schwartz函數(shù)來定義的,

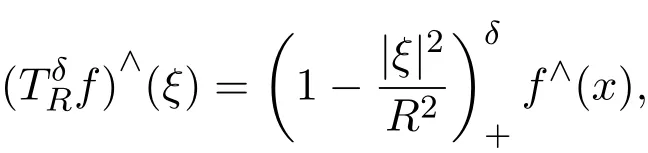
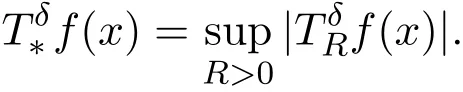
這些算子首先是由Bochner引進(jìn)的,它們與多重Fourier級數(shù)的求和密切相關(guān)并且在調(diào)和分析的研究中起著很重要的作用.設(shè)b是?n上的一個局部可積函數(shù),對于任意給定的R＞0, b和所生成的交換子定義如下:

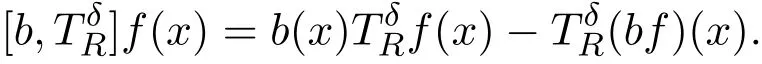
2 主要結(jié)果及證明

從而完成了定理的證明.

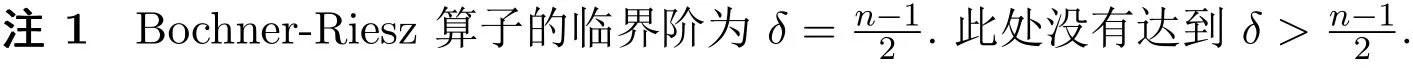
[1]Morrey C B.On the solutions of quasi-linear elliptic partial differential equations[J].Trans.Amer.Math. Soc.,1938,43:126-166.

[2]Komori Y,Shirai S.Weighted Morrey spaces and a singular integral operator[J].Math.Nachr.,2009,282(2): 219-231.

[3]王華.關(guān)于Calder′on-Zygmund算子在加權(quán)Morrey空間上的一些交換子估計[J].中國科學(xué):A輯,2012, 42(1):31-45.

[4]Muckenhoupt B.Weighted norm inequalities for the Hardy maximal functions[J].Trans.Amer.Math.Soc., 1972,165:207-226.

[5]陸善鎮(zhèn),王昆揚.Bochner-Riesz平均[M].北京:北京師范大學(xué)出版社,1988.

[6]Stein E M,Weiss G.Introduction to Fourier Analysis on Euclidean Spaces[M].New Jersey:Princeton Univ. Press,1971.

[7]Paluszy′nski M.Characterization of the Besov spacea via the commutator operator of Coifman,Rochberg and Weiss[J].Indiana Univ.Math.,1995,44:1-17.

[8]Garcia-Cuerva J.Weighted Hpspaces[J].Dissertations Math.,1979,62:1-63.

[9]Hu Guoen,Lu Shanzhen.The maximal operator associated with the commutator of the Bochner-Riesz operator[J].Beijing Math.,1996,21:96-106.

[10]周民強(qiáng).調(diào)和分析講義[M].北京:北京大學(xué)出版社,1995.

[11]王華.Bochner-Riesz算子在加權(quán)Morrey空間上的一些估計[J].數(shù)學(xué)學(xué)報,2012,55(3):552-560.

[12]P′erez C.Endpoint estimates for commutators of singular integral operators[J].Funct.Anal.,1995,128:163-185.

[13]Stein E M.Harmonic Analysis:Real-Variable Methods,Orthogonality,and Oscillatory Integrals[M].Princeton:Princeton University Press,1993.

Boundedness of the commutator of Bochner-Riesz operators on weighted Morrey spaces

Zhang Shanshan,Qu Meng,Shu Lisheng
(College of Mathematics and Computer Science,Anhui Normal University,Wuhu241003,China)

In this paper,we use a method of sharp maximal function to show the boundedness of commutator generated by Bochner-Riesz operators and weighted BMO function on the weighted Morrey spaces under appropriate conditions on the weight.

Bochner-Riesz operators,weighted Morrey spaces,weighted BMO spaces

O174.2

A

1008-5513(2013)02-0214-07

10.3969/j.issn.1008-5513.2013.02.016

2012-12-05.

安徽省高校自然科學(xué)項目(KJ2011A138).

張姍姍(1989-),碩士生,研究方向:調(diào)和分析.

2010 MSC:42B25