First-principles Study of Electronic Structures,Elastic Properties and Thermodynamics of the Binary Intermetallics in Mg-Zn-Re-Zr Alloy
Gang CHEN*,Peng ZHANG
First-principles Study of Electronic Structures,Elastic Properties and Thermodynamics of the Binary Intermetallics in Mg-Zn-Re-Zr Alloy
Gang CHENa,b,*,Peng ZHANGb
aDepartment of Engineering,University of Leicester,University Road,Leicester LE1 7RH,UKbSchool of Materials Science and Engineering,Harbin Institute of Technology at Weihai,Weihai 264209,China
The electronic structures,elastic properties and thermodynamics of MgZn2,Mg2Yand Mg2La have been determined from the f i rst-principle calculations.The calculated heats of formation and cohesive energies show that Mg2La has the strongest alloying ability and structural stability. The structural stability mechanism is also explained through the electronic structures of these phases.The ionicity and metallicity of the phases are estimated.The elastic constants are calculated;the bulk moduli,shear moduli,Young’s moduli,Poisson’s ratio value and elastic anisotropy are derived;and the brittleness,plasticity and anisotropy of these phases are discussed.Gibbs free energy,Debye temperature and heat capacity are calculated and discussed.
Copyright?2013,China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.
Magnesium alloy;Electronic structure;Elastic property;Thermodynamic property;First-principles
1.Introduction
Mg-Zn-Re-Zr alloy is a commonly used deformation magnesium alloy in aerospace industry because of its excellent properties,suchashigh-temperaturestrength,excellent corrosion resistance and anti-oxidation properties[1-6]. MgZn2,Mg2Y and Mg2La phases,as strengthening phase,are believed to be the key components affecting the properties of Mg-Zn-Re-Zr alloy.They belong to the typical AB2type Laves phase and play an important role in ref i ning the grains and improving the mechanical properties and creep resistance [7].Therefore,it is important to study the electronic structures, elastic properties and thermodynamics of MgZn2,Mg2Y and Mg2La.
The f i rst-principles techniques have been widely applied to study the physical properties of intermetallic compound.There are many reports on the properties of MgZn2,Mg2Y and Mg2La.Zhou et al.[8]researched the structure stabilities and elastic properties of MgZn2phase.Wang et al.[9]studied the structural stabilities and electronic characteristics of Mg2La phase.Zhang et al.[10]calculated the enthalpies of formation of Mg2Y and Mg2La.Ganeshan et al.[11]calculated the elastic constants of Mg2La.Wrobel et al.studied the thermodynamic and mechanical properties of Mg2La[12].Almost all of the above research focused on the enthalpies of formation,electronic structures and the physical properties such as elastic constants,elastic modulus and Poisson’s ratio.However,minimal focus has been placed on the thermodynamics properties of MgZn2,Mg2Y and Mg2La.In general,the thermodynamicpropertiesofintermetalliccompoundsare important because some thermodynamic properties,such as Gibbs free energy,Debye temperature and heat capacity,can determinethethermodynamicstabilityofsystem.Themeasurement of thermodynamic property of intermetallic compounds is often challenging.Recently,the f i rst-principles based on the density functional theory investigations of thermodynamic properties of metals have given some quite satisfactory results for Gibbs free energy and heat capacity [13-19].Therefore,it seems to be interesting to investigate the thermodynamic properties of MgZn2,Mg2Y and Mg2La phases by using the f i rst-principles.
In this paper,the electronic structures,elastic properties and thermodynamics of MgZn2,Mg2Y and Mg2La will be analyzed with f i rst-principles method.The results are discussed in comparison with the available experimental values. The structures are optimized by full relaxation,and the lattice parameters are obtained.The heat of formation and the cohesive energy are calculated and discussed.The structural stability mechanism is also explained through the electronic structures of these phases.The elastic constants are calculated, the bulk modulus,shear modulus,Young’s modulus,Poisson’s ratio value and elastic anisotropy are derived,and the brittleness and plasticity of these phases are researched by empirical criterion.Gibbs free energy,Debye temperature and heat capacity from phonon calculations are discussed.This study will provide useful data for analysis and design of Mg-Zn-Re-Zr alloy,and also for future measurements of MgZn2,Mg2Y and Mg2La.
2.Computational methods
The total energy,elastic properties and electronic structure are calculated by using Cambridge sequential total energy package(CASTEP),in which the f i rst-principles plane-wave pseudo-potentials method based on density functional theory (DFT)is adopted[20].The ultrasoft pseudo potentials[21]are employed to represent the interactions between ionic core and valence electrons.For Mg,Zn,Yand La,the valence electrons consideredare2p63s2,3d104s2,4s24p64d15s2and 5s25p65d16s2,respectively.A special k-point sampling method was used for the integration by setting 6×6×4 for MgZn2, 5×5×4 for Mg2Y and 5×5×5 for Mg2La,respectively. Perdew-Wang(PW91)[22]version of the generalized gradient approximation(GGA)[23]is used for calculating the exchange-correlation energy.A kinetic energy cut-off value of 340 eV[24]is used for plane wave expansion.The total energy changes during the optimization f i nally converging to less than 1×10-6eV and the forces per atom are reduced to 0.02eV/°A.TheBroyden-Fletcher-Goldfarb-Shannon (BFGS)algorithm is applied to relax the whole structure to reach the ground state where both cell parameters and fractional coordinates of atoms are optimized simultaneously.All calculations are performed with the non-spin polarized density functional theory.The DMol program is used for the calculation of thermodynamic properties of phases[25-27].As for as the calculation of Gibbs free energy is concerned,at f i rst, the simulation of molecular dynamics is done,the motion direction and strength of each atom and other information are obtained based on the frequency analysis by the use of cell optimizationconf i guration,someenergiesofvibration, rotation and translation at different temperatures are given by the integrated treatment of the movement information of all the atoms in order to calculate the entropy and enthalpy of the unit cell,and f i nally,the Gibbs free energy is calculated by using the standard statistical thermodynamic formulas.In the calculation of Gibbs free energy,each compound is relaxed for 0.01 ps with a time step of 1.0 fs through NVT molecular dynamics.The BLYP exchange-correlation function is adopted for GGA correction.All-electron Kohn-Sham wave functions are expanded in a double numerical basis with polarized orbit(DNP).
3.Results and discussion
3.1.Crystal structures and lattice constants
The crystal structures of MgZn2,Mg2Y and Mg2La phases are shown in Fig.1.The crystal structural parameters and lattice constants are listed in Tables 1 and 2.The structures are optimized by full relaxation,and the equilibrium lattice parameters of MgZn2,Mg2Y and Mg2La phases are derived and listed in Table 2.The calculated results are compared with others experimental and analytical results[8,10,12,28,29].It can be found that the calculated lattice parameters are in good agreement with the experimental values and other theoretical values,with the difference between them being less than 0.5%, especially,our calculated lattice parameters are closer to the experimental values compared with other theoretical values,so the present calculations are highly reliable.
3.2.Heat of formation and cohesive energy
Negative heat of formation usually means an exothermic process,the lower the heat of formation is,the stronger the alloying ability is.To analyze the alloying abilities of MgZn2, Mg2Y and Mg2La phases,their heats of formation(ΔH)are calculated by the following expression[30]
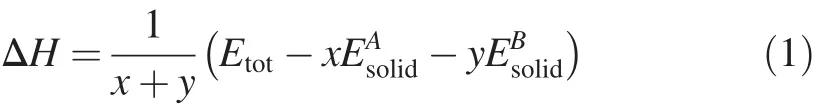
where Etotis the total energy of the unit cell,x and y are the numbers of Mg,Zn,Y and La atoms,respectively,EAsolidand are the energies of each Mg,Zn,Y and La atoms in the solid states.The calculated energies of Mg,Zn,Y and La atomsforourconsideredsystemsare-978.4696, -1711.1724,-1053.1388and-863.0929eV/atom, respectively.
The obtained heats of formation of MgZn2,Mg2Y and Mg2La calculated by Eq.(1)are listed in Table 2.The calculated heats of formation of Mg2Y are in good agreement with the experimental result and other theoretical value,but the calculated heats of formation of MgZn2and Mg2La are quite different from the experimental results.This difference may be attributed to that our calculation method is different from others and the temperature calculated here is 0 K.Further analysis found that the heats of formation of MgZn2,Mg2Yand Mg2La were all negative,conf i rming that the structures of these phases can exist stably.The values of heats of formation decrease in the sequence of Mg2Y>MgZn2>Mg2La.It can be seen that Mg2La phase has the strongest alloying ability among them.
Cohesive energy is def i ned as the energy which releases when the crystal is decomposed into single atoms.The lower the cohesive energy is,the higher the structure stability is.To estimate their phase stabilities,their cohesive energies(Ecoh) are calculated by the following expression
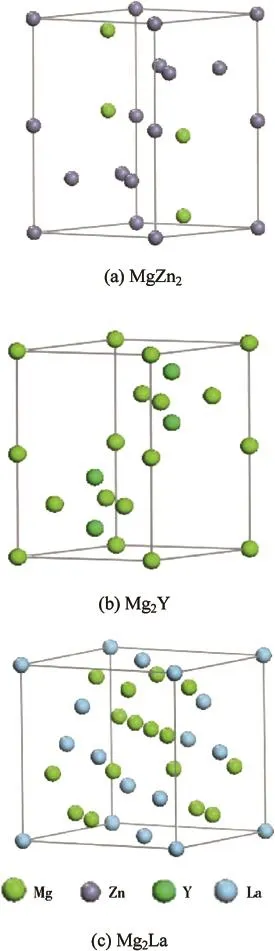
Fig.1.The crystal structures.
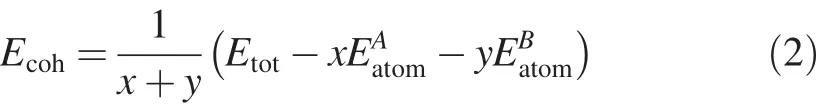
where Ecohis the total energy of the unit cell used in the present calculation,x and y are the numbers of Mg,Zn,Yand La atoms in unit cell,respectively,and EAatomand EBatomare the energies of isolated Mg,Zn,Y and La atoms in the free state, respectively.The calculated energies of Mg,Zn,Y and La isolated atoms are-976.0772,-1708.0388,-1047.8932 and -857.8028 eV/atom,respectively.
The calculated results of the cohesive energies of MgZn2, Mg2Y and Mg2La are shown in Fig.2.The negative cohesive energies of MgZn2,Mg2Y and Mg2La show their energetic stabilization.From the calculated values,it can be further found that the cohesive energy decreases in the sequence of MgZn2>Mg2Y>Mg2La.Hence,Mg2La phase has the strongest structural stability among them.
3.3.Electronic structures
In the present work,the total and partial densities of states (DOS)are calculated to have a further insight into the bonding of MgZn2,Mg2Y and Mg2La phases and then to reveal the structural stability mechanism of these phases.The total and partial densities of states of MgZn2,Mg2Y and Mg2La phases are shown in Fig.3.It can be seen from Fig.3 that the main bonding peaks of all phases basically fall within-10 eV to 0 eV,and originate from the contribution of valence electron numbers of Zn(s),Zn(d),Mg(s)and Mg(p)orbits for MgZn2(Fig.3(a));but for Mg2Y,those are the result of the bonding orbits of Y(s),Y(p),Y(d),Mg(s)and Mg(p)orbits (Fig.3(b));for Mg2La,those mainly originate from the contribution of valence electron numbers of La(s),La(p), La(d),Mg(s)and Mg(p)orbits(Fig.3(c)).From Fig.3(d),it is found that the number of bonding electrons(per atom)of MgZn2is 1.5445 between the Fermi level and-10 eV,which is smaller than 2.2197 of Mg2Y and 2.3002 of Mg2La.The smaller the number of bonding electrons is,the weaker the interaction of charges is[31].Hence,Mg2La has the strongest structural stability among them.The same result can be obtained through cohesive energy analysis,conf i rming the conclusion from the electronic structure point of view.
Thepopulationanalyticalresultscanprovidemore insightful information on chemical bonding.The calculated results are listed in Table 3.It is seen from Fig.3 that the charges of Mg are transferred to Zn in MgZn2,and thetransferred charges(1.05×4)are 4.2;for Mg2Y,the charges (0.06×4)of Mg(I)transferred to Mg(II)and Y are 0.24;but for Mg2La,the charges(0.18×4)of La transferred to Mg are 0.72.The calculated results indicate that the ionicity of these compounds gradually increases in the order of Mg2Y<Mg2La<MgZn2.
The metallicity of the compound is estimated by Li[32]

Table 1Crystal structural parameters of MgZn2,Mg2Y and Mg2La phases.
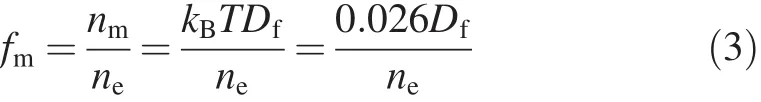
where Dfis the DOS value at the Fermi level in unit state/ eV cell,T is the temperature,nmand neare the thermally excited electrons and the valence electron density of cell, respectively,kBis the Boltzmann constant,neis calculated by ne=N/Vcell,N is the total number of valence electrons,and Vcellis the cell volume.From the related parameters and calculated results listed in Table 4,we can observe that fmincreases in the following sequence:MgZn2<Mg2La<Mg2Y.Thus,the maximal and minimal“metallicities”correspond to Mg2Y and MgZn2,respectively.
The electron density difference,which is def i ned as the electron density difference between the isolated atoms and their bonding states,ref l ects directly their bonding nature,as shown in Fig.3.The contour lines are plotted from -0.02833e/°A3to0.08057e/°A3withtheintervalof 0.01729 e/°A3.The red(in web version)lines correspond to higher density region,and the blue(in web version)lines correspond to lower density region.From Fig.4(a),it is found that the metallic Mg-Mg bonds,the covalent Zn-Zn bonds and the ionic Mg-Zn bonds exist in MgZn2.In Fig.4(b),the metallic Y-Y bonds,the covalent Mg-Mg bonds and the ionic Mg-Y bonds are found in Mg2Y.Fig.4(c)also shows the metallic La-La bonds,the covalent Mg-Mg bonds and the ionic Mg-La bonds.Generally,the charge density distributions show that,for the AB2-type phase,there are mostly metallic bonding between A and A,the covalent bonding between B and B and the ionic bonding between A and B, which is a common feature for the electronic structure in AB2type binary phase[33].
3.4.Elastic properties
The elastic properties of Mg,MgZn2,Mg2Y and Mg2La will be discussed in this section.Mg,MgZn2,Mg2Y and Mg2La belong to the hexagonal and cubic structures,respectively.The hexagonal structure has 5 independent elastic constants:C11,C12,C13,C33and C44,and the cubic structure has 3 elastic constants:C11,C12and C44.The corresponding mechanical stability conditions are C11>0,C11-C12>0, C44>0,(C11+C12)C33-2C213>0 for the hexagonal structure,and are C44>0,C11>|C12|,C11+2C12>0 for the cubic structure.The calculated elastic constants of Mg, MgZn2,Mg2Yand Mg2La are listed in Table 5.As can be seen in Table 5,these conditions are easily satis fi ed,and the obtained elastic constants are close to the available theoretical and experimental values.Therefore,the calculated elastic constants are credible,and the calculated conditions selected in this paper should be suitable.
Mg2La phase is cubic structure.The bulk modulus B and shear modulus G are calculated as follows[34]
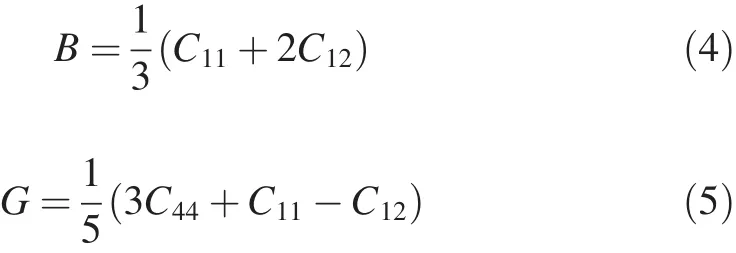

Table 2Lattice constants and heats of formation of MgZn2,Mg2Y and Mg2La phases.
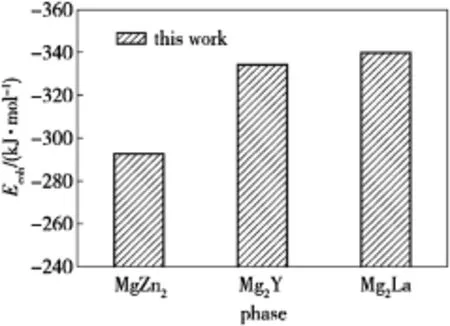
Fig.2.Cohesive energies(Ecoh)of MgZn2,Mg2Y and Mg2La phases.
The structures of Mg,MgZn2and Mg2Y phases are hexagonal.The bulk modulus B and shear modulus G are calculated as follows[35]
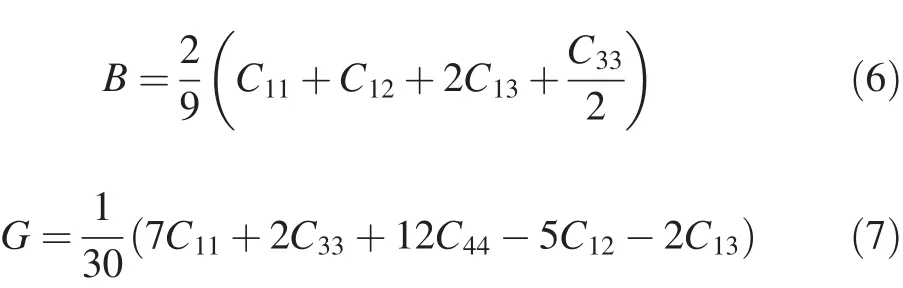
The Poisson’s ratio ν and Young’s modulus E of Mg, MgZn2,Mg2Y and Mg2La are deduced according to the following formula
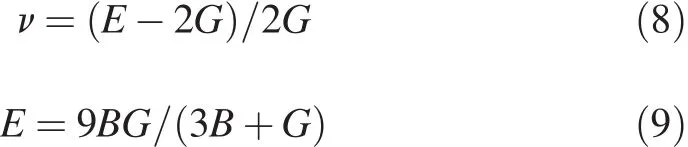
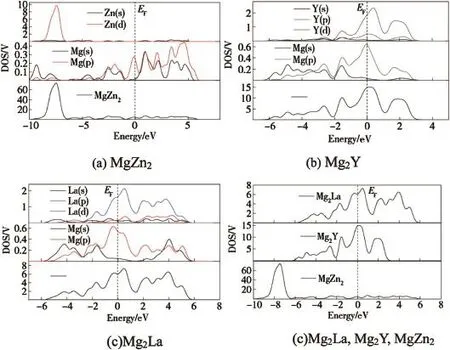
Fig.3.Densities of states of MgZn2,Mg2Y and Mg2La phases.
Table 6 lists the calculated elastic moduli Poisson’s ratios and universal elastic anisotropy indexes.The bulk modulus is usually assumed to be a measure of resistance to volume change by applied pressure,so the larger bulk moduli of MgZn2and Mg2Y show that they have stronger resistance to volume change by applied pressure.Besides,the shear modulus is a measure of resistance to reversible deformation upon shear stress.If the value of shear modulus is larger,the directional bonding between atoms is more pronounced.The calculated results demonstrate that Mg2Y has the largest shear modulus,and then followed by Mg2La and MgZn2.Hence,the directional bonding in Mg2Y would be much stronger those that in Mg2La and MgZn2.Furthermore,Young’s modulus provides a measure of stiffness of the solid.The larger the Young’s modulus is,the stiffer the material is.From the calculated values we found that Young’s modulus of Mg2Y is 59.48 GPa larger than those of Mg2La and MgZn2,indicating that Mg2Y is much stiffer than Mg2La and MgZn2.As indicated above,the elastic moduli of the three phases are larger than that of pure Mg.Hence,it is obvious that their mechanical properties are improved after alloying.
The ratio of shear modulus to bulk modulus of phase can be used to predict the brittle and ductile behaviors of materials.A high(low)G/B value is associated with brittleness(ductility). The critical value separating ductility from brittleness is about 0.57.In the present work,the values of Mg,MgZn2,Mg2Yand Mg2La are 0.539,0.328,0.569 and 0.613,respectively, implying that Mg2La is brittle,while Mg,MgZn2and Mg2Y are ductile.On the other hand,the Poisson’s ratio is used to quantify the stability of the crystal against shear,which usually ranges from-1 to 0.5.The bigger the Poisson’s ratio is, the better the plasticity is.Most of the calculated Poisson’s ratios are very close to 0.25,which means that most of thematerials are with predominantly central interatomic forces [36].MgZn2has the biggest Poisson’s ratio among the three materials considered in this paper.
All single crystals in practice are anisotropic,so an appropriate parameter is needed to characterize the extent of anisotropy.Recently,Ranganathan and Ostoja-Starzewski[37] summarized the existing anisotropy theories,and concluded that most of them are lack of universality because of their nonuniqueness and ignoring a large part of the elastic stiffness tensor.Then they developed a new universal anisotropy index, AU,which can be calculated by the following equation
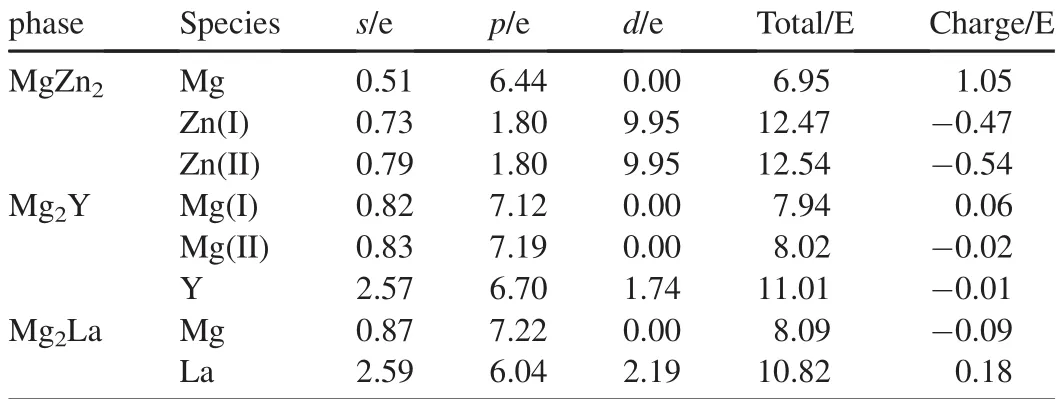
Table 3Mulliken electron populations of MgZn2,Mg2Y and Mg2La phases.
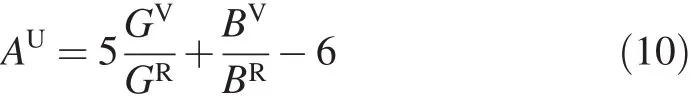
where GV,BV,GRand BRare the shear moduli and bulk moduli estimated using Voigt and Reuss methods,respectively. The anisotropy indexes of Mg,MgZn2,Mg2Y and Mg2La are listed in Table 6,from which,we can conclude that the bulk and shear moduli values calculated by Voigt method are close to those calculated by Reuss method,and the difference between shear moduli calculated with Voigt and Reuss methods has a signif i cant effect on AU.The anisotropy decreases in the following sequence:Mg>MgZn2>Mg2La>Mg2Y.Besides pure Mg,MgZn2behaves more anisotropy than Mg2Y and Mg2La.

Table 4Df,N,Vcelland fmof MgZn2,Mg2Y and Mg2La phases.
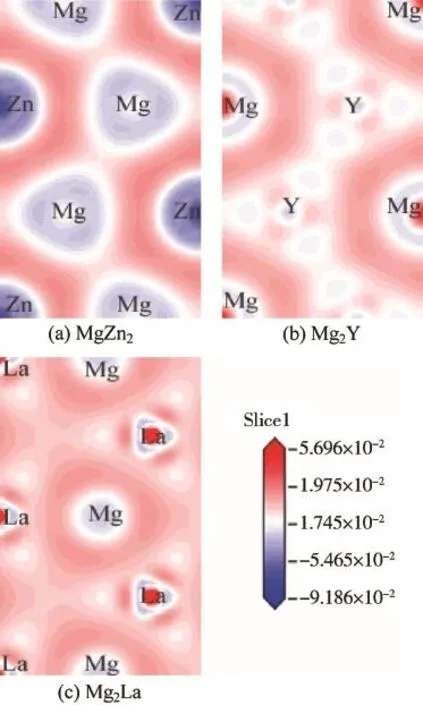
Fig.4.The contour plots of density difference of electronic charges on(001) plane.
3.5.Thermodynamic stability
Here,the thermodynamic property is used to describe the structural stabilities of these compounds with the elevated temperature,especially their Gibbs free energy(G).The Gibbs free energy G of the calculated Mg,MgZn2,Mg2Yand Mg2La phases as a function of temperature from 297 to 573 K is depicted in Fig.5.It can be seen from Fig.5 that the values of the Gibbs free energy at the same temperature gradually decreaseinthefollowingsequence:Mg>Mg2Y>MgZn2>Mg2La.The smaller the Gibbs free energy is,the better the thermal stability of compound is[34].Hence,the calculated results of the Gibbs free energy show that the thermal stabilities of these compounds gradually increase in the following sequence:Mg<Mg2Y<MgZn2<Mg2La.The thermal stabilities of MgZn2,Mg2Y and Mg2La phases arebetter than that of pure Mg and do not change with the elevated temperature,that is to say,the addition of Zn,Y,La addition to the magnesium alloy can improve the heat resistance by forming MgZn2,Mg2Y and Mg2La phases.
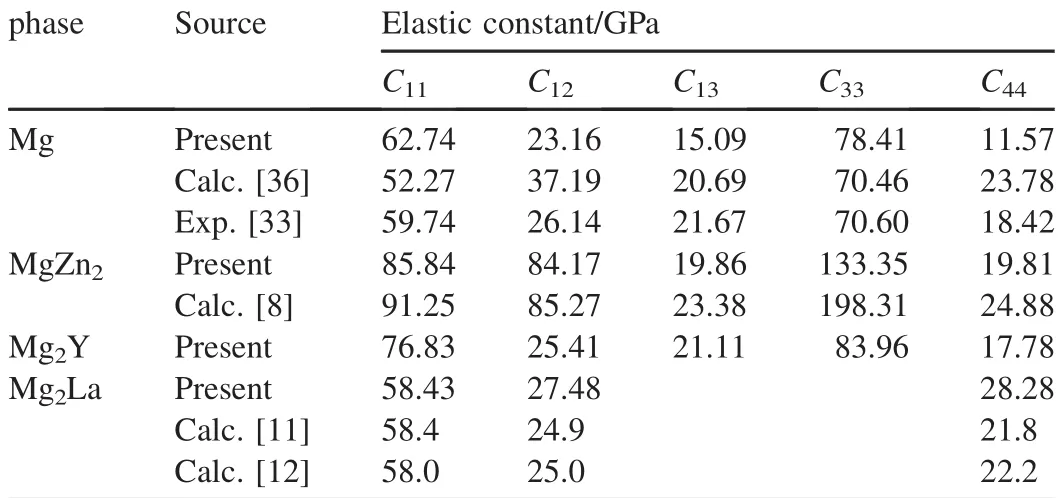
Table 5The calculated and experimental elastic constants of MgZn2,Mg2Y and Mg2La phases.
Once the elastic constants and electronic structures of the compound are known,one can calculate the Debye temperature and heat capacity at the low-temperature.Debye temperature can be used to predict the thermodynamics of material from the elastic properties;it can be also used to distinguish between high-and low-temperature regions for a solid.For T>ΘD,all modes have energy of kBT,and for T<ΘD,one expects the high-frequency modes to be frozen [38].ΘDcan be estimated from the average sound velocity by the following equations[39]
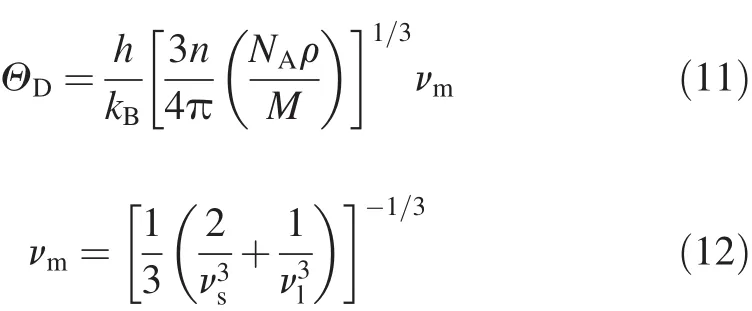
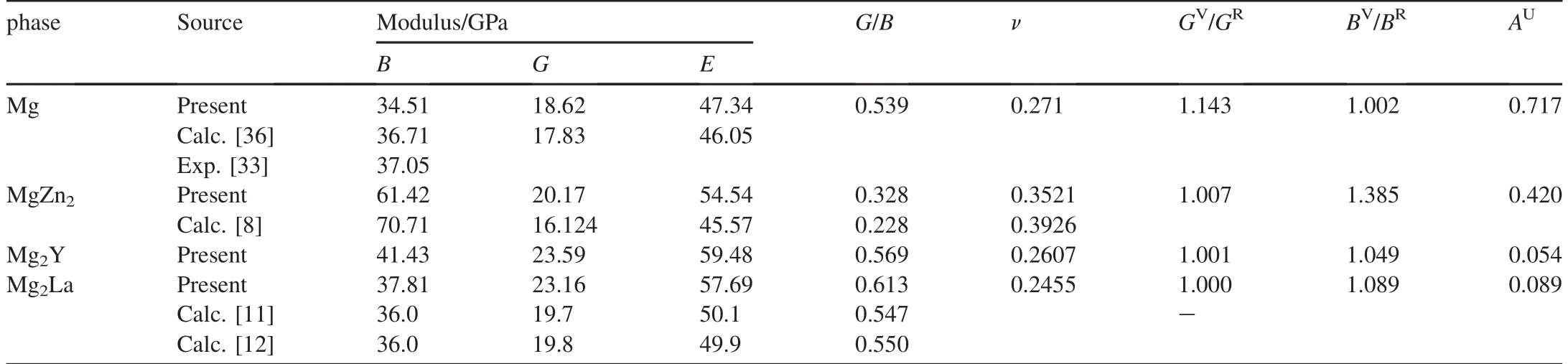
Table 6The calculated and experimental elastic moduli,Poisson’s ratios and universal elastic anisotropy indexes of MgZn2,Mg2Y and Mg2La phases.
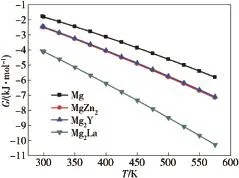
Fig.5.The Gibbs free energies of Mg,MgZn2,Mg2Y and Mg2La phases as functions of temperature.
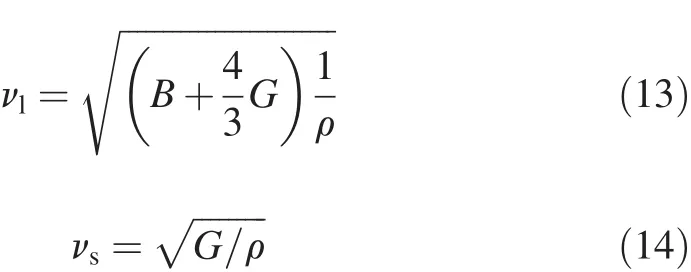
where ΘDis the Debye temperature,h and kBare the Planck and Boltzmann constants,respectively,n is the total number of atoms per formula,NAis the Avogadro number,M is the molecular weight per formula,vmis the average sound velocity,vlis the longitudinal sound velocity,and vsthe shear sound velocity.The calculated results of ΘD,vland vsare listed in Table 7.The largest ΘDis 317.02 K for Mg2Y.It is known that ΘDcan be used to characterize the strength of covalent bonds in solids.From Table 7,we can conclude that the covalent bond in Mg2Y is stronger than those in other phases.Besides,the sequence of ΘDfor these phases is Mg2Y>Mg2La>MgZn2,which is consistent with the observed trend of Young’s modulus and shear modulus,as shown in Table 6.From the values of ΘD,Young’s modulus and shear modulus,we may conclude that the mechanical stability of Mg2Y is the best among three phases.
Besides,since MgZn2,Mg2Y and Mg2La phases studied in the present paper have the metallic feature at the Fermi level, the calculations of the electronic structures and elastic constants enable us to estimate the heat capacity(cp)at the lowtemperature,which is given as
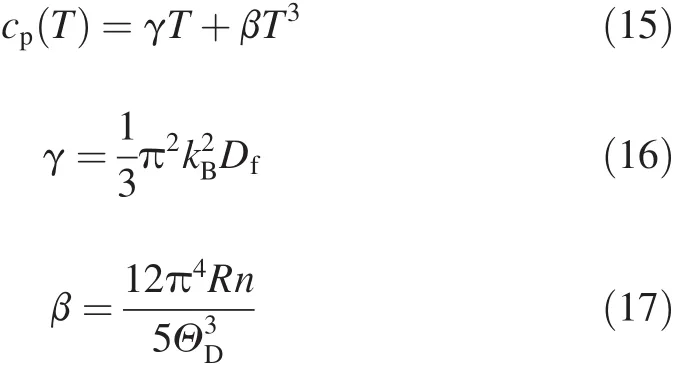

Table 7Theoretically calculated thermal properties of MgZn2,Mg2Y and Mg2La phases.

Fig.6.Heat capacities of MgZn2,Mg2Y and Mg2La phases in the range of 0-25 K.
where γ and β are the coeff i cients of electronic and lattice heat capacities,respectively;n is the total number of atoms per formula unit;R is the molar gas constant.Heat capacity is an invaluable tool to explore the fundamental properties of materials.Note that ΘD,as a rule,only describes the temperature dependence of cpfor T<ΘD/10[40].Fig.6 shows cpvs T in the range of 0-25 K for three phases.As can be seen from Fig.6,the main contribution to cpis the excitation of electrons at 13 K,the values of cpchange in the sequence of Mg2Y>Mg2La>MgZn2,and the change of cpis consistent with the change of γ,indicating the heat capacities are determined by the electrons at f i rst;besides,in Table 7,the smallest value of γ=10.1431×10-3J/(K2mol)is attributed to MgZn2,and because it has the smallest DOS value at the Fermi level(Df),MgZn2has the weakest metallic nature among three phases.In the range of 13-25 K,the contribution from phonon excitation must be taken into account.As a result,the growth trend of cpis MgZn2>Mg2La>Mg2Y, which is the same as the sequence of β.Thus,it can conclude that the heat capacity is determined by the electron excitation at very low temperatures(near 0 K),and the contribution from phonon excitation is signif i cant at high temperature.
4.Conclusions
The electronic structures,elastic properties and thermodynamics of MgZn2,Mg2Y and Mg2La were determined from fi rst-principles calculation.The calculated heats of formation and cohesive energies show that Mg2La has the strongest alloying ability and structural stability.The calculations of bonding electron numbers show that Mg2La has the strongest structural stability.The calculated elastic constants show that three phases are mechanically stable.The calculated bulk moduli B,shear moduli GU,Young’s moduli E,Poisson ratio ν and elastic anisotropy Ashow that Mg2La is brittle,while MgZn2and Mg2Y are ductile;the stiffness of Mg2Y is the highest;MgZn2has the best plasticity and anisotropy among three phases.The calculations of thermodynamic properties show that the Gibbs free energies of MgZn2,Mg2Yand Mg2La decrease,while the heat capacity Cvincreases with the elevated temperature.The calculated results of the Gibbs free energy show that the thermal stability of these compounds gradually increases in the order of Mg2Y<MgZn2<Mg2La. The calculated Debye temperature,Young’s modulus and shear modulus show that the mechanical stability of Mg2Y is the best among three phases.
Acknowledgments
We are grateful for the support of the National Natural Science Foundation of China(NSFC)for support under Grant No.51005217.Dr.Chen is grateful for the support from China Postdoctoral Science Foundation Grant No.20100480677.
[1]Li YG,Liu SR,Liu HL.Mechanical properties and microstructure of MB26 alloy under different condition of hot working process.Chin J Rare Met 2004;28:942-6[in Chinese].
[2]Chen Q,Shu DY,Zhao ZD,Zhao ZX,Wang YB,Yuan BG.Microstructuredevelopmentandtensilemechanicalpropertiesof Mg-Zn-RE-Zr magnesium alloy.Mater Des 2012;40:488-96.
[3]Chen Q,Yuan BG,Zhao GZ,Shu DY,Hu CK,Zhao ZD,et al.Microstructural evolution during reheating and tensile mechanical properties of thixoforged AZ91D-RE magnesium alloy prepared by squeeze castingsolid extrusion.Mater Sci Eng A 2012;537:25-38.
[4]Chen Q,Zhao ZD,Zhao ZX,Hu CK,Shu DY.Microstructure development and thixoextrusion of magnesium alloy prepared by repetitive upsetting-extrusion.J Alloy Compd 2011;509:7303-15.
[5]Chen Q,Lin J,Shu DY,Hu CK,Zhao ZD,Kang F,et al.Microstructure development,mechanical properties and formability of Mg-Zn-Y-Zr magnesium alloy.Mater Sci Eng A 2012;554:129-41.
[6]Bettles CJ,Gibson MA.Microstructural design for enhanced elevated temperature properties in sand-castable magnesium alloys.Adv Eng Mater 2003;12:859-65.
[7]Mordike BL.Creep-resistant magnesium alloys.Mater Sci Eng A 2002;324:103-12.
[8]Zhou DW,Xu SH,Zhang FQ.First-principles calculations of structural stabilities and elastic properties of AB(2)type intermetallics in ZA62 magnesium alloy.Acta Metall Sin 2010;46:97-103.
[9]Wang YF,Zhang WB,Wang ZZ.First-principles study of structural stabilities and electronic characteristics of Mg-La intermetallic compounds.Comput Mater Sci 2007;41:78-85.
[10]Zhang H,Shang SL,Saal JE.Enthalpies of formation of magnesium compoundsfromf i rst-principlescalculations.Intermetallics 2009;17:878-85.
[11]Ganeshan S,Shang SL,Zhang H.Elastic constants of binary Mg compoundsfromf i rst-principlescalculations.Intermetallics 2009;17:313-8.
[12]Wrobel J,Hector LG,Wolf W.Thermodynamic and mechanical properties of lanthanum-magnesium phases from density functional theory.J Alloy Compd 2012;512:296-310.
[13]Shang SL,Wang Y,Kim DE.First-principles thermodynamics from phonon and Debye model:application to Ni and Ni3Al.Comput Mater Sci 2010;47:1040-8.
[14]Zhao KM,Jiang G,Wang LL.Electronic and thermodynamic properties ofB2-FeSifromf i rstprinciples.PhysicaBCondensMatter 2011;406:363-7.
[15]Pang MJ,Zhan YZ,Wang HZ.Structural,electronic,elastic and thermodynamic properties of AlSi2RE(RE=La,Ce,Pr and Nd)from f i rstprinciple calculations.Comput Mater Sci 2011;50:3303-10.
[16]Xiao B,Feng J,Zhou CT,Xing JD,Xie XJ,Cheng YH,et al.The elasticity,bond hardness and thermodynamic properties of X2B(X=Cr, Mn,Fe,Co,Ni,Mo,W)investigated by DFT theory.Physica B Condens Matter 2010;405:1274-8.
[17]Hector LG,Herbst JF,Wolf W.Ab initio thermodynamic and elastic properties of alkaline-earth metals and their hydrides.Phys Rev B 2007;76:014121.1-18.
[18]Herbst JF,Hector LG.Structural discrimination via density functional theory and lattice dynamics:monoclinic Mg2NiH4.Phys Rev B 2009;79. 155113-1,7.
[19]Herbst JF,Hector LG.Energetics of the Li amide/Li imide hydrogen storage reaction.Phys Rev B 2005;72.125120-1,8.
[20]Shi DM,Wen B,Melnik R.First-principles studies of Al-Ni intermetallic compounds.J Solid State Chem 2009;182:2664-9.
[21]FaganSB,MotaR,BaierleRJ.Stabilityinvestigationandthermalbehavior of a hypothetical silicon nanotube.J Mol Struct 2001;539:101-6.
[22]Pack JD,Monkhors HJ.Special points for Brillouin zone integrations’-a reply.Phys Rev B 1977;16:1748-9.
[23]Perdew JP,Burke K,Ernzerh M.Generalized gradient approximation made simple.Phys Rev Lett 1996;77:3865-8.
[24]NykenJ,GarciaFJ,MoselBD.Structuralrelationships,phasestabilityand bondingofcompoundsPdSnn(n=2,3,4).SolidStateSci2004;6:147-55. [25]Hector LG,Herbst JF.Electronic structure calculations for LaNi5and LaNi5H7:energeticsandelasticproperties.JAlloyCompd 2003;353:74-85.
[26]Shang SL,Hector LG.First-principles study of elastic and phonon properties of the heavy fermion compound CeMg.J Phys Condens Matter 2009;21(24):246001-12.
[27]Hector LG,Herbst JF.Density functional theory for hydrogen storage materials:successesandopportunities.JPhysCondensMatter 2008;20(6):64229-39.
[28]Li CH,Hoe JL,Wu P.Empirical correlation between melting temperature and cohesive energy of binary Laves phases.J Phys Chem Solids 2003;64:201-12.
[29]Miedema AR,Dechatel PF,Deboer FR.Cohesion in alloys-fundamentals of a semi-empirical model.Physica B+C 1980;100:1-28.
[30]Chen L,Peng P,Li GF.First-principle calculation of point defective structures of B2-RuAl intermetallic compound.Rare Metal Mater Eng 2006;35:1065-70.
[31]Zhou DW,Liu JS,Xu SH.Thermal stability and elastic properties of Mg3Sb2and Mg3Bi2phases from f i rst-principles calculations.Physica B Conden Matter 2010;405:2863-8.
[32]Li YF,Gao YM,Xiao B.Theoretical study on the stability,elasticity, hardness and electronic structures of W-C binary compounds.J Alloy Compd 2010;502:28-37.
[33]Yu WY,Wang N,Xiao XB,Tang BY,Peng LM,Ding WJ.First-principles investigation of the binary AB2 type Laves phase in Mg-Al-Ca alloy: electronicstructureandelasticproperties.SolidStateSci2009;11:1400-7. [34]Anderson OL.A simplif i ed method for calculating the Debye temperature from elastic constants.J Phys Chem Solids 1963;24:909-17.
[35]Kanoun MB,Goumri-Said S,Reshak AH.Theoretical study of mechanical,electronic,chemical bonding and optical properties of Ti2SnC, Zr2SnC,Hf2SnC and Nb2SnC.Comput Mater Sci 2009;47:491-500.
[36]Mattesini M,Ahuja R,Johansson B.Cubic Hf3N4and Zr3N4:a class of hard materials.Phys Rev B 2003;68.184108.
[37]Ranganathan SI,Ostoja-Starzewski M.Universal elastic anisotropy index.Phys Rev Lett 2008;101(5).055504.
[38]Mayer B,Anton H,Bolt E.Ab-initio calculation of the elastic constants and thermal expansion coeff i cients of Laves phases.Intermetallics 2003;11:23-32.
[39]Deligoz E,Ciftci YO,Jochym PT.The f i rst principles study on PtC compound.Mater Chem Phys 2008;111:29-33.
[40]Drulis MK,Czopnik A,Drulis H.On the heat capacity of Ti3GeC2.Mater Sci Eng B 2005;119:159-63.
25 April 2012;revised 20 August 2013;accepted 27 August 2013 Available online 3 October 2013
*Corresponding author.School of Materials Science and Engineering, Harbin Institute of Technology at Weihai,Weihai 264209,China.
E-mail address:chengang2003@126.com(G.Chen).
Peer review under responsibility of China Ordnance Society
Production and hosting by Elsevier
2214-9147/$-see front matter Copyright?2013,China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.
http://dx.doi.org/10.1016/j.dt.2013.09.011
- Defence Technology的其它文章
- The Research on Compressive Properties of Polytetraf l uoroethylene at High Strain Rate
- Research on Key Technologies of Detecting 1553B Avionics Data Bus Network
- Application of Space-time Conservation Element and Solution Element Method in Intake and Exhaust Flows of High Power Density Diesel Engine
- Research on Optical Properties and Micro-processing Characteristics of Collodion Thin Film
- The Spatial Color Mixing Model of Digital Camouf l age Pattern
- Design Method of Equipment Optimization Development Based on Standardization Theory

