王彩玲, 高慧巖

(1. 吉林大學(xué) 數(shù)學(xué)學(xué)院, 長春 130012; 2. 北京中科金財(cái)科技股份有限公司, 北京 100083)

文獻(xiàn)[1-6]利用抽象次微分對(duì)單目標(biāo)規(guī)劃問題進(jìn)行了研究. 本文利用抽象次微分給出目標(biāo)函數(shù)為弱凸函數(shù)的向量優(yōu)化問題的最優(yōu)性條件, 推廣了文獻(xiàn)[1-6]的結(jié)果.

1 抽象凸函數(shù)的概念

考慮如下多目標(biāo)規(guī)劃問題：

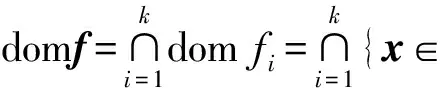
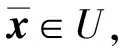
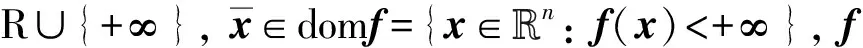
?x∈Rn}.

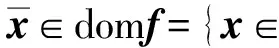
?x∈Rn}.

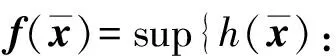
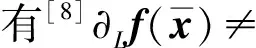
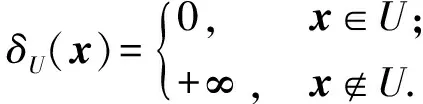
2 最優(yōu)性條件

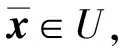
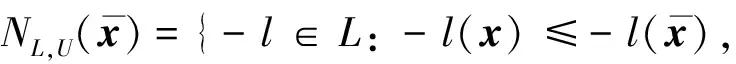
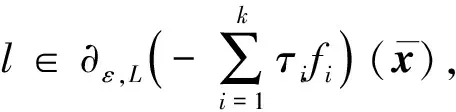
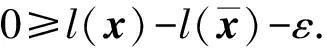
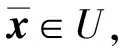
證明： 首先, 證明

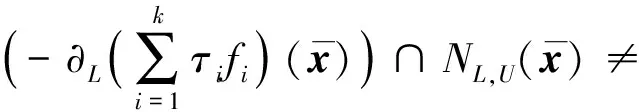
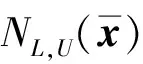
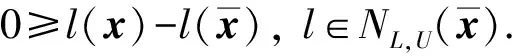
其次, 證明

由于

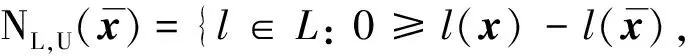
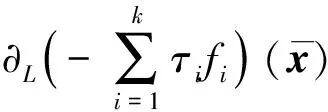
(1)

又因?yàn)?/p>

(2)

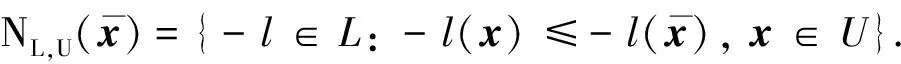
(3)

[1] Jeyakumar V, Rubinov A M, WU Zhi-you. Sufficient Global Optimality Conditions for Non-convex Quadratic Minimization Problems with Box Constraints [J]. Journal of Global Optimization, 2006, 36(3): 471-481.

[2] Jeyakumar V, Rubinov A M, WU Zhi-you. Non-convex Quadratic Minimiation Problems with Quadratic Constraints: Global Optimality Conditions [J]. Mathematical Programming, 2007, 110(3): 521-541.

[3] WU Zhi-you, Jeyakumar V, Rubinov A M. Sufficient Conditions for Globally Optimality of Bivalent Nonconvex Guadratic Programs with Inequality Constraints [J]. Journal of Optimization Theory and Applications, 2007, 133(1): 123-130.

[4] WU Zhi-you. Sufficient Global Optimalty Conditions for Weakly Convex Minimizition Problems [J]. Journal of Optimization Theory and Application, 2007, 39(3): 427-440.

[5] Jeyakumar V, Rubinov A M, WU Zhi-you. Generalized Fenchel’s Conjugation Formulas and Duality for Abstract Convex Function [J]. Journal of Optimization Theory and Application, 2007, 132(3): 441-458.

[6] WU Zhi-you, Rubinov A M. Global Optimality Conditions for Some Classes of Optimization Problems [J]. Journal of Optimization Theory and Application, 2010, 145(1): 164-185.

[7] 林銼云, 董加禮. 多目標(biāo)優(yōu)化的方法與理論 [M]. 長春： 吉林教育出版社, 1992.

[8] Rubinov A M. Abstract Convexity and Global Opimization [M]. Dordencht: Kluwer Academic Publishers, 2000.

[9] WANG Cai-ling, GAO Hui-yan. Optimality Conditions of Multiobjective Programming Problerms Based on the Astract Convexity [J]. Journal of Jilin University: Science Edition, 2012, 50(4): 698-700. (王彩玲, 高慧巖. 抽象凸多目標(biāo)規(guī)劃的最優(yōu)性條件 [J]. 吉林大學(xué)學(xué)報(bào): 理學(xué)版, 2012, 50(4): 698-700.)