Influences of soil hydraulic and mechanical parameters on land subsidence and ground fissures caused by groundwater exploitation*
CHEN Xing-xian (陳興賢)
School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, China
Bureau of Geology Mineral Resources Prospecting of Jiangsu Province, Nanjing 210018, China, E-mail: js_cxx@sina.com
LUO Zu-jiang (駱祖江), ZHOU Shi-ling (周世玲)
School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, China
Influences of soil hydraulic and mechanical parameters on land subsidence and ground fissures caused by groundwater exploitation*
CHEN Xing-xian (陳興賢)
School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, China
Bureau of Geology Mineral Resources Prospecting of Jiangsu Province, Nanjing 210018, China, E-mail: js_cxx@sina.com
LUO Zu-jiang (駱祖江), ZHOU Shi-ling (周世玲)
School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, China
(Received January 27, 2013, Revised August 15, 2013)
In order to study the influences of hydraulic and mechanical parameters on land subsidence and ground fissure caused by groundwater exploitation, based on the Biot’s consolidation theory and combined with the nonlinear rheological theory of soil, the constitutive relation in Biot’s consolidation theory is extended to include the viscoelastic plasticity, and the dynamic relationship among the porosity, the hydraulic conductivity, the parameters of soil deformation and effective stress is also considered, a threedimensional full coupling mathematical model is established and applied to the study of land subsidence and ground fissures of Cangzhou in Hebei Province, through the analysis of parameter sensitivity, the influences of soil hydraulic and mechanical parameters on land subsidence and ground fissure are revealed. It is shown that the elastic modulusE, the Poisson ratioν, the specific yieldμand the soil cohesionchave a great influence on the land subsidence and the ground fissures. In addition, the vertical hydraulic conductivityzkand the horizontal hydraulic conductivityskalso have a great influence on the land subsidence and the ground fissures.
Biot’s consolidation, viscoelastic plasticity, groundwater, land subsidence, ground fissure
Introduction
Serious geological disasters related with the land subsidence and the ground fissure were caused by excessive exploitation of the groundwater in China’s north China plain and the Yangtze River delta since the 1980s. The land subsidence and the ground fissure caused by the groundwater excessive exploitation was shown to be a complex process in which the seepage interacts with the stress field[1]. The process is closely related to the soil hydraulic and mechanical parameters. Therefore, the influences of the soil hydraulic and mechanical parameters on the land subsidence caused by the groundwater excessive exploitation are the key to simulate and predict the land subsidence accurately. In China, the history of the model research of the land subsidence caused by the groundwater exploitation may date back more than 10 years, with Shanghai and Tianjin as representative research centers. However, in these models the groundwater flow model is almost a quasi three-dimensional model, with only the flow equation in the aquifer and without one in aquitard to simulate the water level change. It would be difficult to determine the land subsidence caused by the aquitard water release[2,3]. The land subsidence models are usually vertical one-dimensional linear elastic models, based on the Terzaghi theory, and they can not be used to simulate and forecast the soil horizontal deformation, and the occurrence of the ground fissure[4,5]. The dynamic relationship among the soil deformation parameters, the permeability and the stress fields is not well established[6-8], neither the full coupling between the seepage and the land subsidence. Thus it is difficult to accurately determine theinfluences of the soil hydraulic and mechanical parameters on the land subsidence by using these models. The objective of this paper is based on the Biot’s consolidation theory combined with the nonlinear rheological theory of soil, to extend the constitutive relation in Biot’s consolidation theory to include the viscoelastic plasticity, with consideration of the dynamic relationship among the porosity, the hydraulic conductivity, the parameters of soil deformation and effective stress, and to establish a three-dimensional full coupling mathematical model and to apply it to the study of land subsidence and ground fissures of Cangzhou in Hebei Province. On the basis of the model calibration and the analysis of parameter sensitivity, the influences of the soil hydraulic and mechanical parameters on the vertical displacement (land subsidence) and the horizontal displacement (ground fissures) are studied. It is shown that the elastic modulusE, the Poisson ratioν, the specific yieldμand the soil cohesionchave a great influence on the land subsidence and the ground fissures. In addition, the vertical hydraulic conductivityzkand the horizontal hydraulic conductivityskalso have a great influence on the land subsidence and the ground fissures.
1. Biot’s consolidation theory
For a saturated soil, assuming that the soil skeleton deformation is linear elastic and small, the seepage satisfies the Darcy’s law, the water is incompressible or with a micro compression, the three dimensional Biot’s consolidation equation can be expressed as follows[9]:
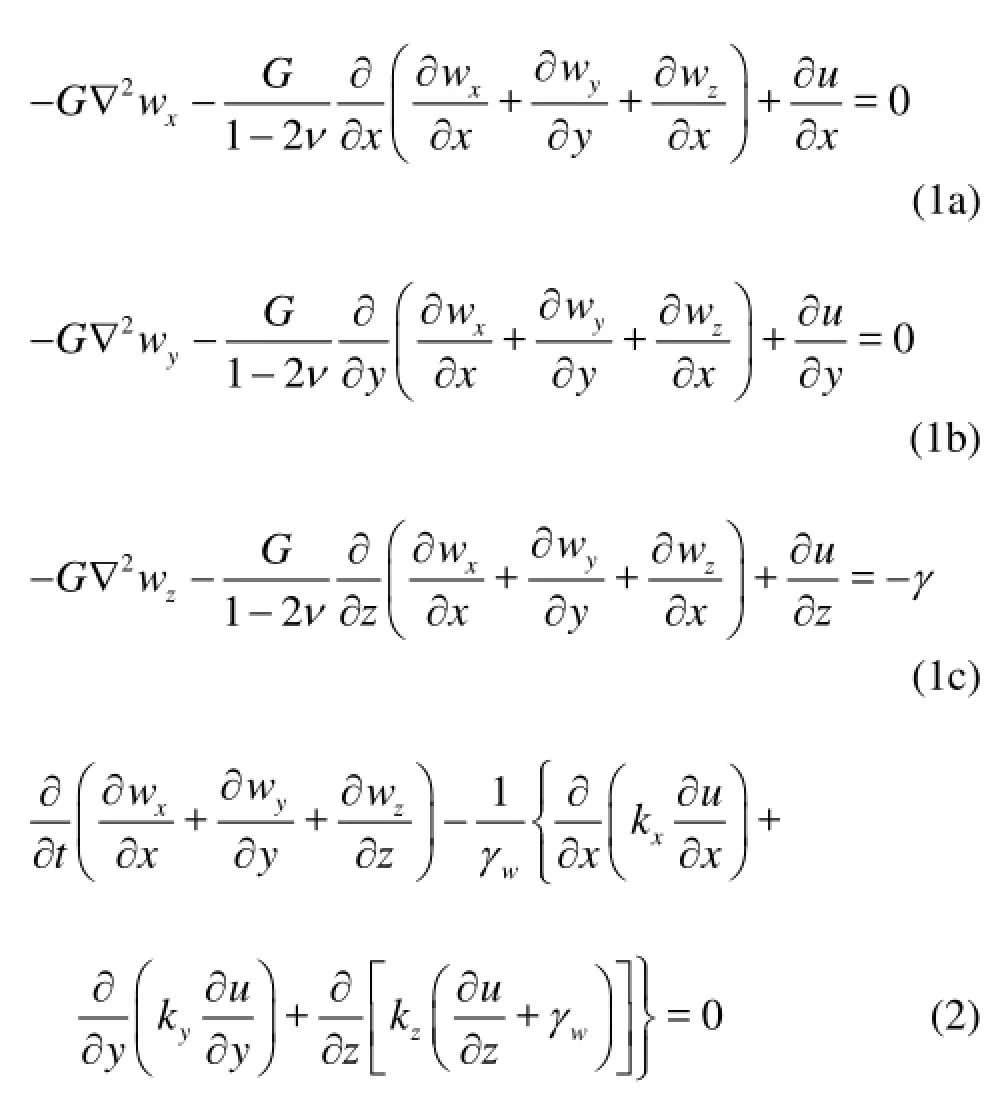

2. Constitutive model of soils


3. Visco-elastic-plastic finite element equation of Biot’s consolidation
The Galerkin weighted residual method is used to discretize the equations. With the nonlinear characteristics of soils, the incrementtΔ is used, and Eqs.(1) and (2) are discretized into an incremental form as[11]


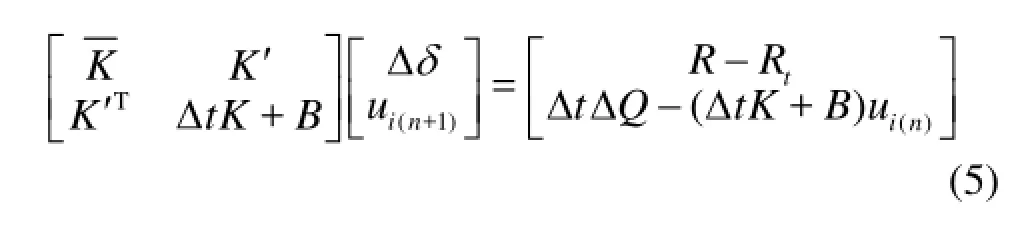
This is the three-dimensional finite element equation of Biot’s consolidation, and can be solved under appropriate conditions[12].
4. Dynamic model of parameters
(1) Nonlinearity of porosity and hydraulic conductivity
Actually, the fluid-solid coupling is related with various porosity effects on permeability of soils, and the pore pressure dissipation leads to the deformation of the soil skeleton, as evidenced as the soil consolidation deformation in a macroscopic view[13]. Through the assumed conditions of Biot’s consolidation, the dynamical expression of the porositynand the hydraulic conductivitykcan be obtained according to the definition of the porosity and the Kozeny-Carman equation[14]
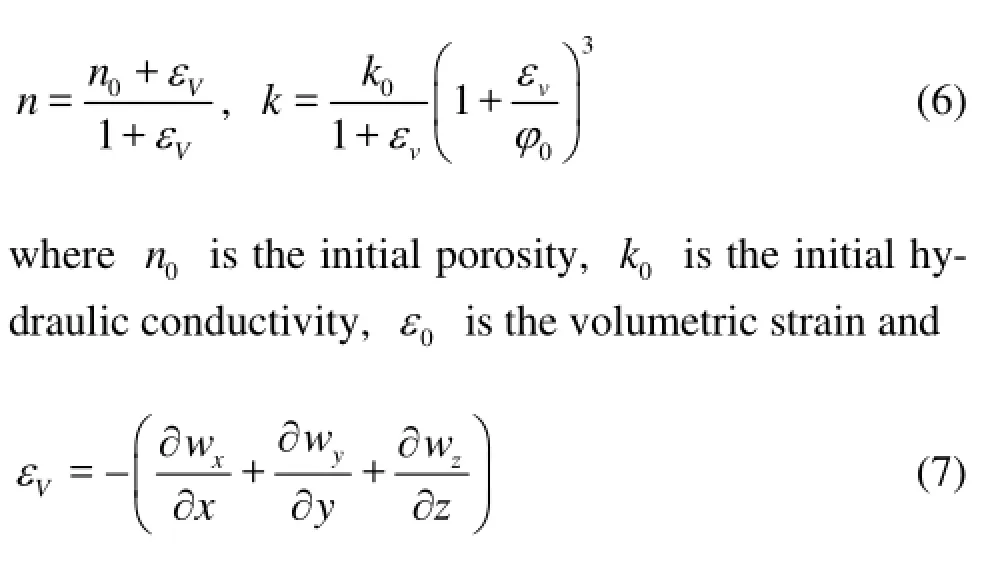
(2) Nonlinearity of soil parameters
Using the Duncan-nonlinear model to extend the constitutive relations of the soil to nonlinear ones, where the elastic constantsEandνin the matrix [D] in constitutive relations {Δσ}=[D]{Δε} are no longer regarded as constant, but they vary with the stress state. The tangent modulus and the Poisson’s ratio are expressed as follows:
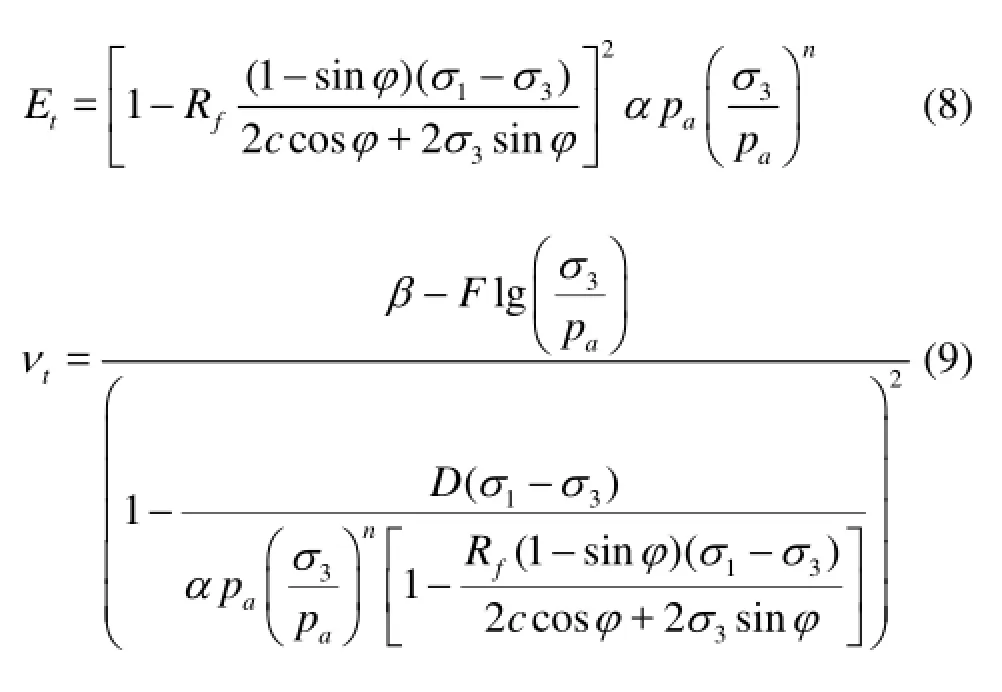
wherefRis the failure ratio,cis the viscous force,φis the internal friction angle,1σis the first principal stress,3σis the third principal stress, lgαandβare the intercepts of the plotted curves of the results of the conventional triaxial compression test,apis the atmospheric pressure, =F0.33, =D4 are the experimental parameters of soil,nis the slope of the results of the conventional triaxial compression test.
5. Conditions for a unique solution
5.1Initial conditions
The initial conditions include the initial ground stress condition, the initial displacement condition and the initial pore pressure condition.
(1) The initial ground stress condition: an estimation of the initial stress based on the gravity of the soil is

wherexσis the initial horizontal stress,zσis the initial vertical stress,zis the depth of the calculating point,0Kis the static lateral pressure coefficient,

5.2Boundary conditions
There are four kinds of boundary conditions: the pore water condition, the impulse boundary condition, the free surface boundary condition and the displacement boundary condition.
(1) The pore water conditions1Γ

wheresuis the known pressure of the pore water on the boundary1Γ.
(2) The impulse boundary conditions2Γ

whereqLis the known discharge per unit area on the boundaryΓ2
(3) The free surface boundary conditionsΓ3
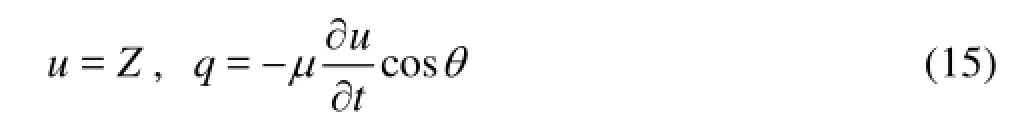
whereμis the specific yield,θis the angle between the normal vector of the outer boundary and the perpendicular direction,qis the discharge per unit area on the boundary3ΓandZis the elevation of the free surface.
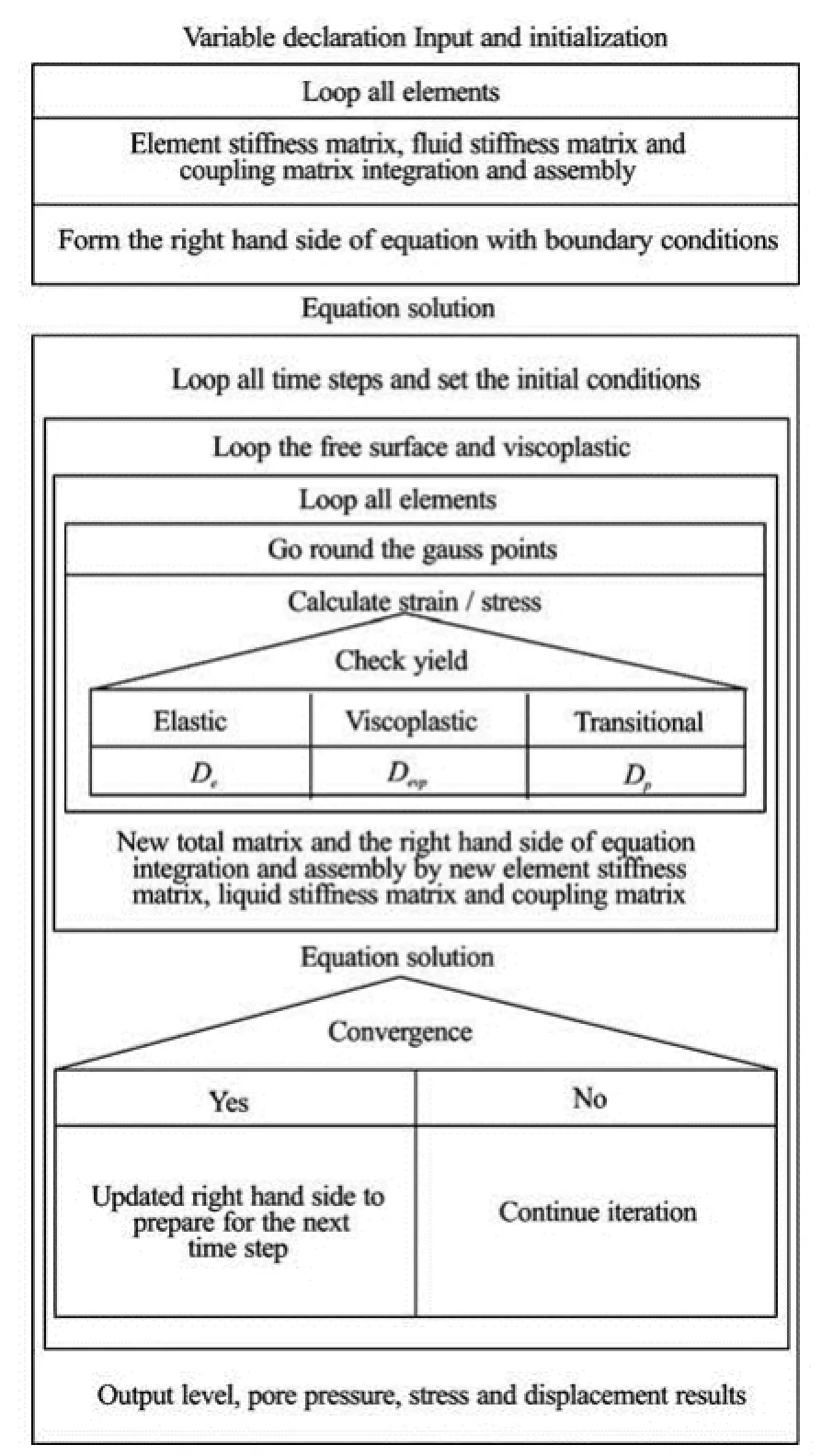
Fig.1 Program structure
(4) The displacement boundary condition4Γ
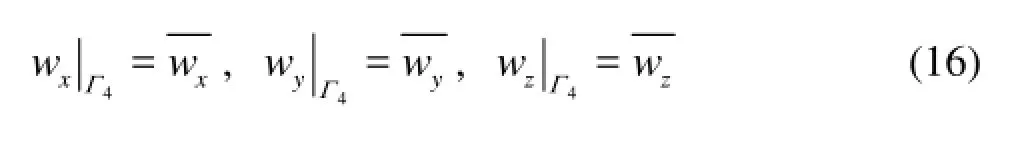

The whole calculation is carried out by a computer program in FORTRAN language, and a finite element numerical simulation software is developed based on the visco-elastic-plastic Biot’s consolidation theory for the groundwater withdrawal and the land subsidence. The program structure is shown in Fig.1.
6. Sensitivity analysis of model parameters
6.1Generalization and discretization of the geological model
Cangzhou in Hebei province is taken as an example. The quaternary loose sediment of Cangzhou is taken as the calculation region, which covers an area of 1.4056×1010m2, with the maximum vertical depth of 350 m. The outside of the area is treated as impulse boundaries. The top of the model system is a recharge boundary to receive precipitation and agricultural irrigation infiltration, and as also a drainage boundary to evaporate the groundwater. The bottom of the model system is an impervious boundary. The discretizations are achieved by use of 8-node hexahedron element, with the subdivisions on the plane of 8 948 rectangular grids. The loose sediments are divided into four layers vertically, as the first phreatic aquifer formation, the second confined aquifer, the third confined aquifer formation and the fourth confined aquifer formation. The subdivisions of the study area are shown in Fig.2.
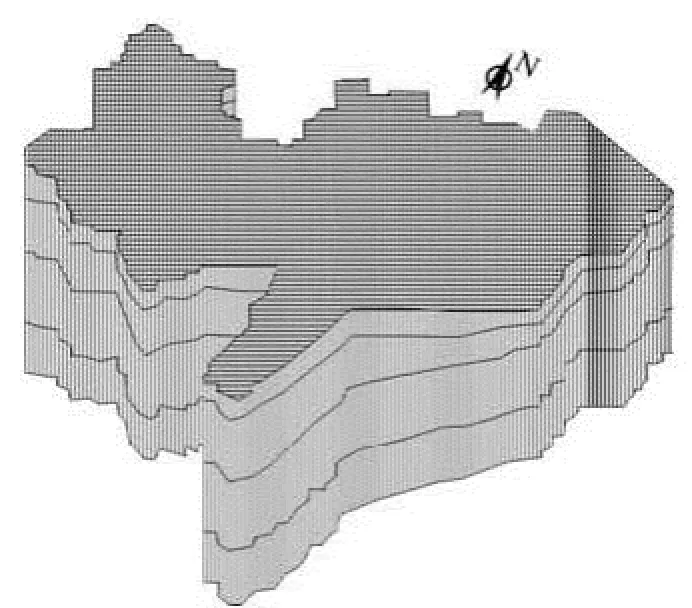
Fig.2 Vertically mesh of the study area
6.2Calibration and validation
The data from 52 observation wells and 300 land subsidence leveling data are chosen for the model calibration and validation. The observation data of the water level and the leveling data of subsidence are collected from December 31st, 2005 to December 31st, 2005. A month is taken as a stress period of exploitation and there are 12 stress periods in total. Meanwhile, there are 10 account steps in each stress period.
The initial pore water pressures of each aquifer are obtained from the conversion of the measured initial water level. The initial displacements of each aquifer and boundary are 0.
Due to the deep buried depth and weak evaporation intensity of the groundwater, the rainfall infiltration and the evaporation of the groundwater are considered as one parameter, named the comprehensive infiltration coefficient.
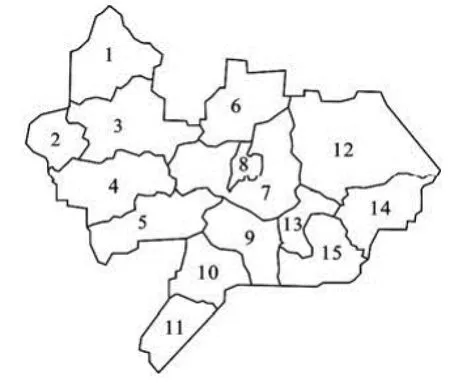
Fig.3 Comprehensive infiltration coefficient zoning map

Table 1 Comprehensive infiltration coefficient values
The comprehensive infiltration coefficient is calculated for 15 zonings after model calibration and validation. The zoning map and the coefficient value of each zoning are shown in Fig.3 and Table 1.
The relevant hydraulic and mechanical parameters are calculated for 69 zonings. The zoning map of the second confined aquifer formation is shown in Fig.4 and the parameter values for each zoning are shown in Table 2. The fitting curves of the water level are shown in Fig.5 and Fig.6, and the land subsidence contour fitting is shown in Fig.7.
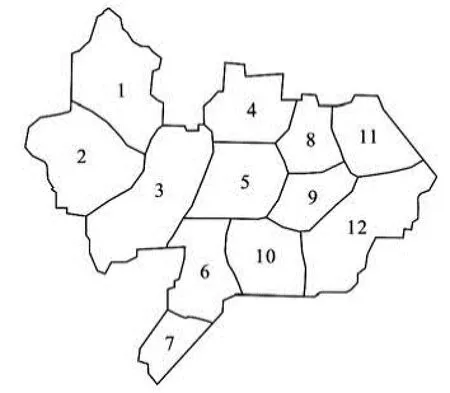
Fig.4 Hydrological parameter zoning map for layer 2
6.3Parameter sensitivity analysis
It is important to accurately determine the model’s parameters, but in practice, the parameters always change greatly on account of the sampling and the sample preparation, the test instrument, the test method and process, the proficiency of the experimenters, data analysis, and so on. It is important to study the influences of parameters on the calculation results, as by the parameter sensitivity analysis[15].

If a tiny change ofixleads to a great change ofX, we will say thatXis sensitive toixandixis a hypersensitivity parameter. On the other hand, if a great change ofixleads to a tiny change ofX, we will say thatXis insensitive toixandixis a hyposensitivity parameter.
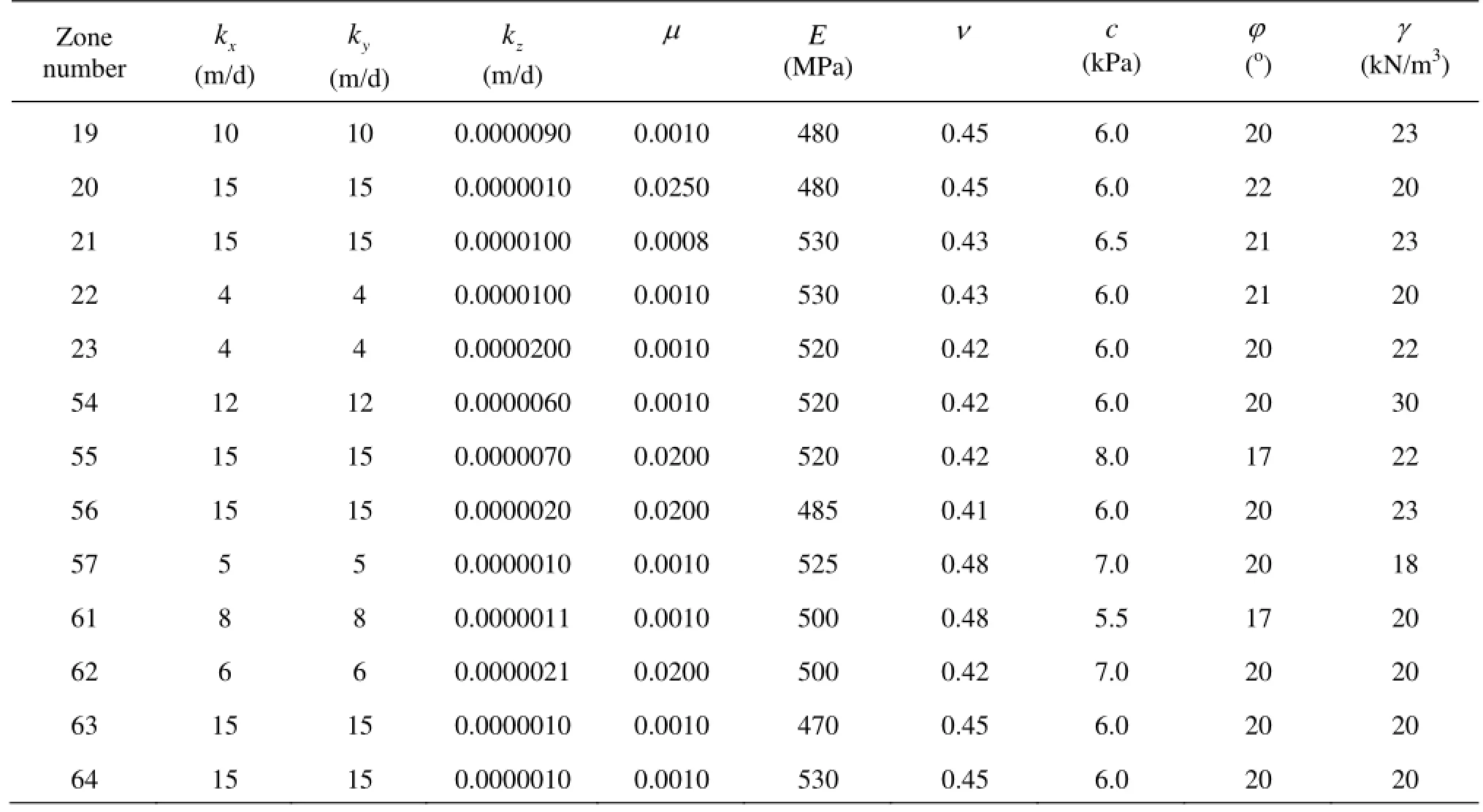
Table 2 The parameter values for each zoning of layer 2
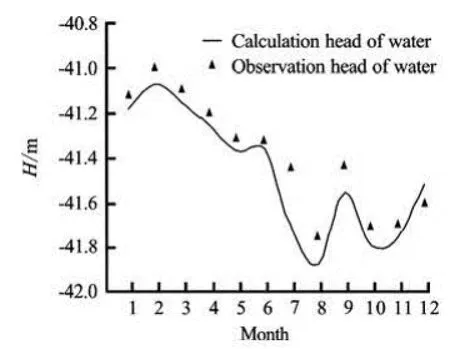
Fig.5 Comparison of simulated results with observation data of groundwater level for well Cangguan12-1, layer 2
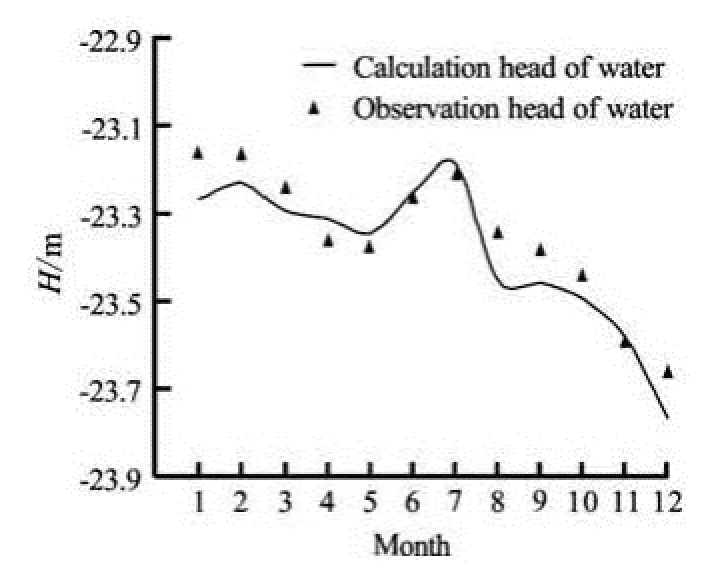
Fig.6 Comparison of simulated results with observation data of Groundwater level for well Huang40-22, layer 2
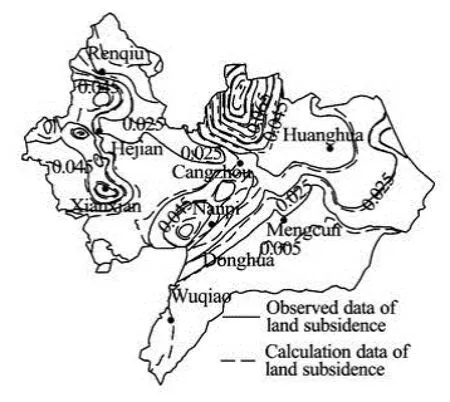
Fig.7 Comparison of simulated results with observation data of land subsidence of 2006
According to the traditional parameter sensitivity analysis, the parameter sensitivity in this case is the partial derivative of the displacement to the parameter. The displacement is sensitive to the parameter if the parameter sensitivity is great. Then the parameter has a greater influence on the land subsidence and the ground fissures. Because the soil hydraulic and mechanical parameters in the coupling model of the groundwater exploitation, the land subsidence and the ground fissures have different dimensions, the sensitivities of different parameters also have different dimensions and they are incomparable. Thus, one can not use the traditional sensitivity to characterize the sensitivity of the parameters. On the basis of the finite difference method, the parameter relative sensitivity is defined and used to characterize the sensitivity of the displacement to parameters. The formula is as follows
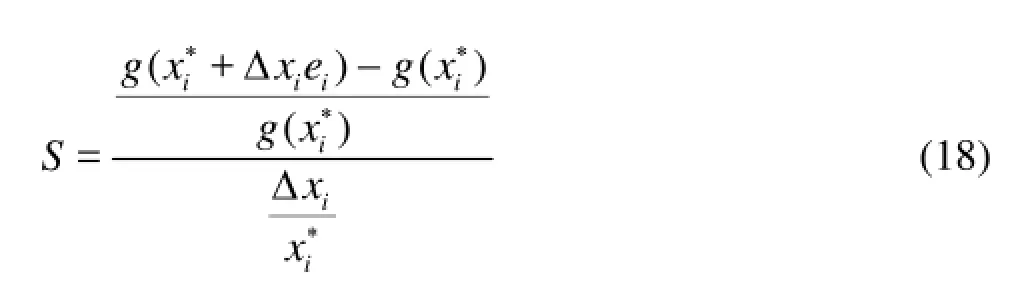


The sensitivity analysis includes 8 parameters: the elastic modulus of the soilE, the Poisson ratioν, the horizontal hydraulic conductivitysk, the vertical hydraulic conductivityzk, the soil cohesionc, the friction angleφ, the specific weight of the soilλand the specific yieldμ. The physical quantities we use to measure the sensitivity include the horizontal displacement and the vertical displacement, as the ground fissures and the land subsidence. The maximal horizontal and vertical displacements of the second confined aquifer are taken as an example. The calculated results are shown in Table 4.
The following conclusion can be made from the results: the elastic modulusE, the Poisson ratioν, the vertical hydraulic conductivityzk, the specific yieldμand the soil cohesionchave great impacts on the vertical displacement, and they are very high sensitive parameters. The horizontal hydraulic conductivitysk, the specific weight of soilλand the friction angleφare high sensitive parameters, their influences on the vertical displacement are relatively weak.
The elastic modulus of the soilE, the Poisson ratioν, the horizontal hydraulic conductivitysk, the specific yieldμand the soil cohesioncare very high sensitive parameters. They have great influences on the horizontal displacement. The influence of the vertical hydrauliczkon the horizontal displacement is relatively weak. The impacts of the friction angleφand the specific weight of the soilλare the lowest, they are sensitive parameters.
6.3.3 Result analysis
(1) The impact of the elastic modulusE: the elastic modulusEis a physical quantity, used to describe the soil’s capability of resisting the deformation. We can conclude from the results that the horizontal displacement is decreased and the vertical displacement is increased when the elastic modulusEis increased. This shows that the land subsidence caused by pumping is smaller in a hard soil than in a soft soil, relatively speaking. Meanwhile, the influences on the displacements are greater when the elastic modulusEis larger. On the other hand, when the elastic modulusEis smaller, the influences are weaker.
(2) The impact of the Poisson’s ratioν: the Poisson’s ratio is a constant used to reflect the lateral deformation of the soil. It is defined as the ratio of the absolute values of the transverse normal strain and the axial normal strain when the soil is under one-way tensile or compressive loading. The calculated results show that the horizontal displacement is increased and the vertical displacement isdecreased when the
Poisson rationνis increased. The amplitude reduction in the vertical displacement is greater than the increased amplitude of the horizontal displacement. This highlights the effects of the horizontal deformation. That is, the effects of the Poisson ratioνon the soil horizontal deformation are very significant. Meanwhile, when the Poisson ratioνis larger, its impacts on the displacement are greater. On the other hand, when the Poisson ratioνis smaller, the impacts are weaker.

Table 4 The results of parameter sensitivity analysis
(3) The impact of the horizontal hydraulic conductivityks: the horizontal hydraulic conductivity is a reflection of the soil permeability in the horizontal direction. It is a main parameter which determines the horizontal seepage and the pore water pressure dissipation. According to the calculated results, the horizontal and vertical displacements are decreased when the horizontal hydraulic conductivityksis increased. This shows that the increase of the horizontal hydraulic conductivityksspeeds up the dissipate rate of the pore water pressure and accelerates the soil consolidation. Meanwhile, the impacts of the horizontal hydraulic conductivitykson the soil displacement are more significant when the horizontal hydraulic conductivity is large. Otherwise, the influences are weak.
(4) The impact of the vertical hydraulic conductivitykz: the vertical hydraulic conductivity is a reflection of the soil permeability in the vertical direction and the closeness of the hydraulic connection of adjacent aquifers. The calculated results show that when the vertical hydraulic conductivitykzis increased, the horizontal and vertical displacements are decreased. This is mainly due to the fact that the increase of the vertical hydraulic conductivitykzstrengthens the hydraulic connection between aquifers, accelerates the water exchange between the various aquifers, slows down the pore water dissipation speed, and the speed of the soil deformation. Meanwhile, the influences of the vertical hydraulic conductivitykzon the displacement are greater when the parameter value is larger. On the other hand, the influences of the vertical hydraulic conductivitykzon the displacement are weaker when the parameter value is smaller.
(5) The impact of the specific yieldμ: the specific yield is a parameter that measures the drainage capacity of gravity and is close to the exchanged water of the free surface. According to the calculated results, the horizontal displacement is decreased and the vertical displacement is increased when the specific yield is increased. This mainly due to the fact that the increase of the specific yieldμstrengthens the capacity of releasing water, speeds up the pore water dissipation speed, and accelerates the vertical deformation of the soil. Meanwhile, when the value of the specific yieldμis larger, the impacts on the displacement are greater. On the other hand, when the value of the specific yieldμis smaller, the impacts on the displacement are weaker.
(6) The impact of the soil cohesionc: the soil cohesion is the mutual attraction between soil particles, and is an index that reflects the soil shear strength. The calculated results show that when the soil cohesioncis increased, the horizontal and vertical displacements are increased, because when the pore water stress dissipates, the increased soil cohesionccan accelerate the soil consolidation and deformation. Moreover, when the value of the soil cohesioncis larger, the influences on the displacement are greater. Otherwise, the influences on the displacement are weaker.
(7) The impact of the friction angleφ: the friction angle is a representation of the soil internal friction, includes the surface frictional forces between soil particles and the bit forces caused by the chain effects of the soil particles. Just like the soil cohesionc, the friction angleφis an important parameter that reflects the soil shear strength. According to the calculated results, when the friction angle is enlarged, the horizontal displacement is decreased and the vertical displacement is increased. Because the enlargement of the friction angle enhances the soil shear strength and reduces the horizontal displacement. Meanwhile, when the friction angle is larger, the impacts on the displacement are greater, otherwise, the impacts are weaker.
(8) The impact of the specific weight of the soilλ: the gravity of unit volume soil is called the specific weight of the soilλ. The calculated results show that when the specific weight of the soilλis increased, the horizontal displacement is increased, and the vertical displacement is decreased. The confining pressure is increased with the increase of the soil gravity and the horizontal displacement is exacerbated significantly. A part of the effective stress is transformed into the confining pressure, and the vertical displacement is relatively decreased. Meanwhile, the impacts on the displacement are increased with the increase of the specific weight of the soilλ.
7. Conclusions
(1) Based on Biot’s consolidation theory and combined with the nonlinear rheological theory of soil, the constitutive relation in Biot’s consolidation theory is extended to include the viscoelastic plasticity, and the dynamic relationship among the porosity, the hydraulic conductivity, the parameters of the soil deformation and the effective stress is also considered, a three-dimensional fully coupled mathematical modelis established. This model considers a perfect coupling among the groundwater exploitation, the land subsidence and the ground fissure caused by the exploitation.
(2) The elastic modulusE, the Poisson ratioν, the specific yieldμand the soil cohesionchave great influences on the vertical displacement (land subsidence) and the horizontal displacement (ground fissures). In addition, the vertical hydraulic conductivitykzand the horizontal hydraulic conductivityksalso have great influences on the vertical displacement (land subsidence) and the horizontal displacement (ground fissures). The impacts of the horizontal hydraulic conductivityks, the specific weight of the soilλand the friction angleφon the vertical displacement (land subsidence) and the vertical conductivitykzon the horizontal displacement (ground fissures) come second. The influences of the friction angleφand the specific weight of the soilλon the horizontal displacement (ground fissure) are the smallest relatively.
(3) The soil hydraulic and mechanical parameters change symmetrically around the reference value, but the influences caused by the parameter changes on the vertical displacement (land subsidence) and the horizontal displacement (ground fissures) are asymmetrical. Compared with the reference value, when the parameter values are large, the influences on the land subsidence and the ground fissures are greater than when the parameter values are small.
[1] CHEN Chong-xi, PEI Shun-ping. A study on water exploitation and land subsidence[J]. Engineering Geology and Hydrogeology, 2001, (2): 5-8(in Chinese).
[2] YANG G. Advances and challenge in research on land subsidence in China[C]. Proceeding of the Seventh International Symposium on Land Subsidence. Shanghai, China, 2005.
[3] LUO Zu-jiang, ZHANG Ying-ying and WU Yong-xia. Finite element numerical simulation of three-dimensional seepage control for deep foundation pit dewatering[J]. Journal of Hydrodynamics, 2008, 20(5): 596-602.
[4] ZHANG Xian-min, TONG Deng-ke and XUE Li-li. Numerical simulation of gas-water leakage flow in a two layered coal bed system[J]. Journal of Hydrodynamics, 2009, 21(5): 692-698.
[5] ZHANG Yan-jun, ZHANG Yan-ji. The numerical analysis of elastic visco-plastic biot’s consolidation to marine soft soil[J]. Journal of Jilin University (Earth Science Edition), 2003, 33(1): 71-75(in Chinese).
[6] PHIEN-WEJ N., GIAO P. H. and NUTALAYA P. Land subsidence in Bangkok, Thailand[J]. Engineering Geology, 2006, 82(4): 187-201.
[7] LI Pei-chao, KONG Xiang-yan and Lu De-tang. Mathematical modeling of flow in saturated porous media on account of fluid-structure coupling effect[J]. Journal of Hydrodynamics, Ser. A, 2003, 18(4): 419-426(in Chinese).
[8] ABIDIN H. Z., ANDREAS H. and GUMILAR I. et al. Land subsidence of Jakarta (Indonesia) and its relation with urban development[J]. Natural Hazards, 2011, 59(3): 1753-1771.
[9] LUO Zu-jiang, LI Hui-zhong and FU Yan-ling. Threedimensional numerical simulation of groundwater dewatering and land- subsidence control in quaternary loose sediments[M]. Beijing, China: Science Press, 2009(in Chinese).
[10] CHEN Xiao-ping, BAI Shi-wei. The numerical aanalysis of visco-elastic-plastic biot’s consolidation for soft clay foundation[J]. Chinese Jounal of Geotechnical Engineering, 2001, 23(4): 481-484(in Chinese).
[11] LIU C.-W., LIN W.-S. and SHANG C. et al. The effect of clay dehydration on land subsidence in the Yun-Lin Coastal Area, Taiwan[J]. Environmental Geology, 2001, 40(4-5): 518-527.
[12] SMIITH I. M. Programming the finite element method[M]. New York, USA: John Wiley and Sons, 2007.
[13] ZHANG Yun, XUE Yu-qun and Wu Ji-chun et al. Land subsidence and earth fissures due to groundwater with drawal in the Southern Yangtze Delta, China[J]. Environmental Geology, 2008, 55(4): 751-762.
[14] LUO Zu-jiang, WANG Yan. 3-D variable parameter numerical model for evaluation of the planned exploitable groundwater resource in regional unconsolidated sediments[J]. Journal of Hydrodynamics, 2012, 24(6): 959-968.
[15] YOU Guang-ming. Numerical platform of elasto-plastic finite element method and its application to geological engineering[D]. Doctoral Thesis, Shanghai, China: Tongji University, 2007(in Chinese).
10.1016/S1001-6058(14)60018-4
* Project supported by the Jiangsu Special Fund (Grant No. dk2012ky01), the Hebei Grand Special Fund (Grant No. CZCG2012055).
Biography: CHEN Xing-xian (1963-), Male, Ph. D.,
Senior Engineer
- 水動力學研究與進展 B輯的其它文章
- Deepwater gas kick simulation with consideration of the gas hydrate phase transition*
- Detrended analysis of Reynolds stress in a decaying turbulent flow in a wind tunnel with active grids*
- Estimation of discharge and its distribution in compound channels*
- A hybrid DEM/CFD approach for solid-liquid flows*
- An ocean circulation model based on Eulerian forward-backward difference scheme and three-dimensional, primitive equations and its application in regional simulations*
- Scale analysis of turbulent channel flow with varying pressure gradient*

