LI Xiao-chao,LI Dong-ya,JIN Quan-qin

(1.Department of Mathematics,Huanghuai University,Zhumadian 463000,China;2.Department of Mathematics,Tongji University,Shanghai 200092,China)

A Class of Solvable Lie Algebras and Their Hom-Lie Algebra Structures

LI Xiao-chao1,LI Dong-ya1,JIN Quan-qin2

(1.Department of Mathematics,Huanghuai University,Zhumadian 463000,China;2.Department of Mathematics,Tongji University,Shanghai 200092,China)

The f i nite-dimensional indecomposable solvable Lie algebras s with Q2n+1as their nilradical are studied and classif i ed,it turns out that the dimension of s is dim Q2n+1+1. Then the Hom-Lie algebra structures on solvable Lie algebras s are calculated.

solvable Lie algebra;nilradical;Hom-Lie algebra;structure

§1.Introduction

The purpose of this paper is to classify a certain type of f i nite-dimensional solvable Lie algebras and give their Hom-Lie algebra structures.These Lie algebras have a specif i c nilradical Q2n+1(n≥2)that in an appropriate basis{X1,X2,···,X2n+1}has the Lie brackets

Levi’s theorem[1]tells us that any fi nite-dimensional Lie algebra is isomorphic to a direct sum of a semi-simple Lie algebra and a maximal solvable ideal.The classi fi cation of fi nitedimensional semi-simple Lie algebras over complex numbers is given in[2].Since any solvable Lie algebra s has a uniquely de fi ned nilradical n,i.e.,maximal nilpotent ideal,satisfying dimn≥ims.Hence we can consider a given nilpotent Lie algebra of dimension n as the nilradicaland then f i nd all of its extensions to solvable Lie algebras.In previous articles this has been performed for some nilpotent Lie algebras,see[3-6].The Scalar f i eld F for algebras considered in this paper is complex number f i eld ?.

Hartwig,Larsson,Silvestrov developed a new approach to the deformation theory of Witt and Virasoro algebras using σ-derivations in[7].They also introduced the concept of Hom-Lie algebra,which is a non-associative algebra satisfying the skew symmetry and the Hom-Jacobi identity.In[8],the authors determined the Hom-Lie algebra structures on semi-simple Lie algebras.We will determine the Hom-Lie algebra structures on some solvable Lie algebras in section 4.

§2.Preliminaries

Any solvable Lie algebra s contains a unique maximal nilpotent ideal,i.e.,the nilradical n.We will assume that n is known,that is,in some basis(X1,X2,···,Xn)we know the LieThe classif i cation of all the solvable Lie algebras s with nilradical n can be achieved by adding further elements Y1,···,Ymto the basis(X1,X2,···,Xn)to form a basis of s.Since the derived algebra of a solvable Lie algebra is contained in the nilradical [2],i.e.,[s,s]?n,we have

The matrix elements of the matrices Bimust satisfy certain linear relations following from the Jacobi relations between the elements(Yi,Xa,Xb).The Jacobi identities between the triples (Yi,Yj,Xb)will provide linear expressions for the structure constantsin terms of the matrix elements of the commutators of the matrices Biand Bj.Since n is the maximal nilpotent ideal of s,the matrices Bimust satisfy another condition;no nontrivial linear combination of them is a nilpotent matrix,i.e.,they are linearly nil-independent.

Now,we will consider the adjoint representation of s,restrict it to the nilradical n and fi nd ad|n(Yi).It follows from the Jacobi identities that ad|n(Yi)is a derivation of n.In other words, fi nding all sets of matrices Biin(2.1)satisfying the Jacobi identities is equivalent to fi nding all sets of outer nil-independent derivations of n

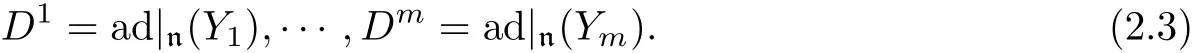
Furthermore,in view of[s,s]?n,the commutators[Di,Dj]must be inner derivations of n.This requirement determines the structure constants,i.e.,the Lie brackets(2.2),up to elements in the center C(n)of n.

Di ff erent sets of derivations may correspond to isomorphic Lie algebras,so redundanciesmust be eliminated.The equivalence is generated by the following transformations

where(Sij)is an invertible m×m matrix,(Tib)is a m×n matrix and the invertible n×n matrix(Rab)must be chosen so that the Lie brackets(1.1)are preserved.

§3.Classif i cation of Solvable Lie Algebras with the Nilradical Q2n+1

The Lie algebra Q2n+1is def i ned by the Lie brackets(1.1)in the introduction,which has degree of nilpotency 2n.In order to obtain all equivalence classes of extensions by non-nilpotent derivations,we f i rst determine the algebra of derivations of Q2n+1.

Theorem 3.1Any outer derivations of Q2n+1are represented by lower triangular matrices in the standard basis{X1,X2,···,X2n+1}.The diagonal elements satisfy

and form of matrix D is

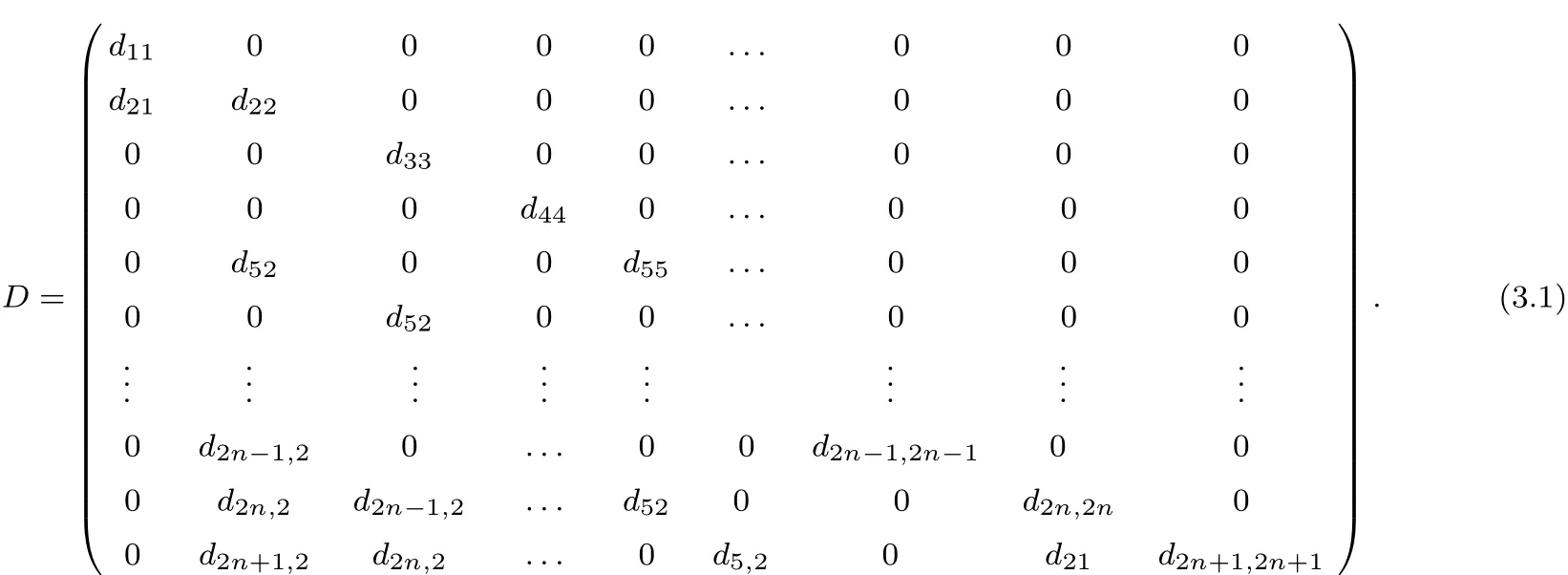
shows that dki=0(3≤i≤2n+1,k＜i).Considering[X2,X3]=0(n≥3)or[X2,X3]=X5(n=2),we have d12=0.Hence,D=(dij)are lower triangular matrices.

Consider the derivations on basis elements Xi,Xj,we get

(C1)i=1,2≤j≤2n?1:dj+1,j+1=d11+djj,d2n+1,j+1=d2n,j+(?1)j+1d2n+1?j,1, dk,j+1=dk?1,j,j+2≤k≤2n;

(C2)i=1,j=2n:d2n+1,2n+1=d11+d2n,2n;

(C3)2≤i≤n,j=2n+1?i:d2n+1,2n+1=dii+d2n+1?i,2n+1?i;

(C4)2≤i≤n?1,i＜j＜2n+1?i:(?1)id2n+1?i,j?(?1)jd2n+1?j,i=0;

(C5)The remaining brackets give no new conditions on the coefficients dij.

From the third equation of case(C1),we by induction obtain

From case(C4),we obtain

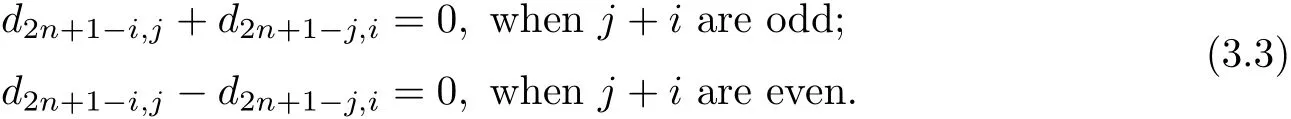
From equations(3.2)and(3.3),we have(not include d2n,2,since i≥2 in(3.3))

By cases(C1),(C2)and(C3),we can easily get

Finally,we can simplify the matrices of the outer derivations by adding suitable inner deriva-we can transform di,1(3≤i≤2n+1)and d32to zero.By the second equation of case(C1),we have

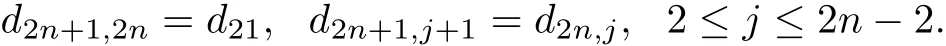
From Theorem 3.1,we know that the diagonal elements of the matrix D can be completely determined by d11.According to the theory of linearly algebra,the number of nil-independent elements m can be at most one since a set of two or more derivations of the form(3.1)cannot be linearly nil-independent.

Theorem 3.2Any solvable Lie algebra s with nilradical Q2n+1will have dimension dims=2n+2.

Here,“solvable”will always mean solvable,indecomposable,non-nilpotent.

Theorem 3.3Precisely one class of solvable Lie algebras s2n+2of dims=2n+2 with nilradical Q2n+1exists.It is represented by a basis{X1,···,X2n+1,Y}and the Lie brackets are

ProofWe rescale D to put d11=1 and change the basis of Q2n+1by several steps.First, let

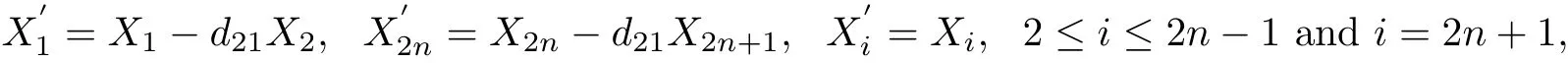
we can change d21to zero.Second,for j=2,3,···,n?1,we let f

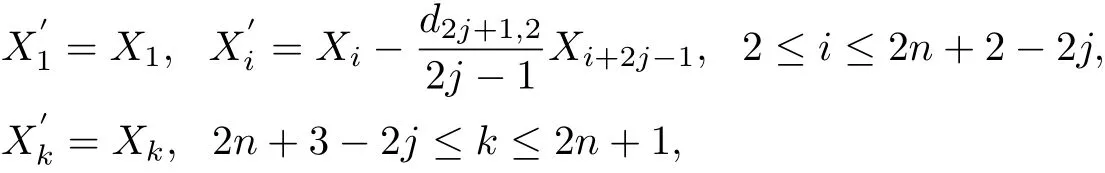
i rst we put d52to zero,then d72etc up to d2n?1,2.Third,let

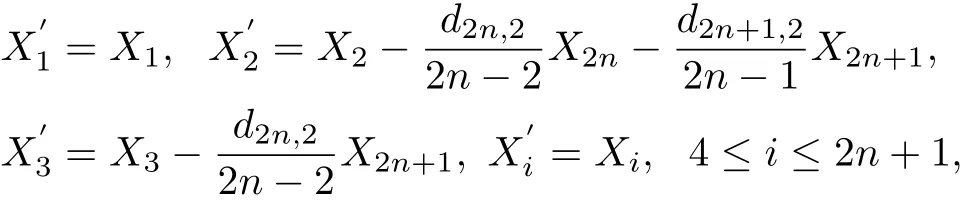
we can change d2n,2,d2n+1,2to zero.

Hence,we have D=diag{1,2,···,2n+1}.The theorem is proved.

§4.Hom-Lie Algebra Structures on s2n+2

The Hom-Lie algebra structures on solvable Lie algebras s2n+2are given in this section.

Def i nition 4.1A Hom-Lie algebra(L,σ)is a non-associative algebra L together with an algebra homomorphism σ:L→L,such that

for all x,y,z∈L,where[,]denotes the product in L.We call Axiom(HL2)the Hom-Jacobi identity.

Theorem 4.1Let s2n+2be a solvable Lie algebra with Lie brackets(3.4).If(s2n+2,σ)is a Hom-Lie algebra,then σ is represented as the following two cases

(i)σ(Xi)=0,1≤i≤2n+1,σ(Y)=c2n?1X2n?1+c2nX2n+c2n+1X2n+1;

(ii)σ(X1)=X1+a2nX2n+a2n+1X2n+1,σ(X2)=X2+a2nX2n+1,σ(Xi)=Xi,3≤i≤2n+1,σ(Y)=Y+(2n?1)a2nX2n?1+2na2n+1X2n+c2n+1X2n+1.

ProofLet σ be a homomorphism on s2n+2.Since[s2n+2,s2n+2]=Q2n+1,we set

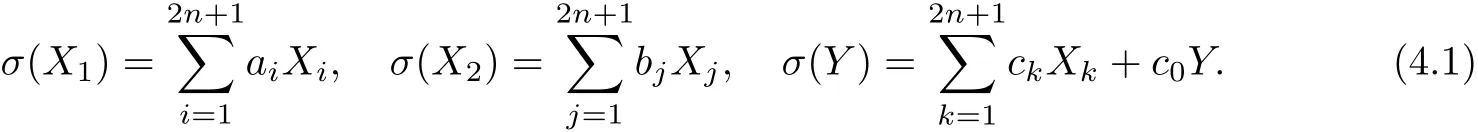
Since σ is a homomorphism on[Y,X1]=X1,[Y,X2]=2X2,we have

(1)If c0=0.Then a1=a2=b1=b2=0,by equation(4.2)and(4.3),we get σ(X1)= a2n+1X2n+1,σ(X2)=b2n+1X2n+1.Since σ(Xi+1)=[σ(X1),σ(Xi)],we have σ(Xi)=0(3≤i≤2n+1).Considering Y,X1,Xj(2≤j≤2n)satisfy Hom-Jacobi identity,we have

That is

Finally,(4.2)and(4.3)imply σ(X1)=σ(X2)=0.The case(i)is proved.

(2)If c0=.Then a1=b1=b2=0,by equation(4.3),we get σ(X2)=Condition σ(Xi+1)=[σ(X1),σ(Xi)]implies σ(Xi)=0(4≤i≤2n+1).Considering Y,X2,X2n?1satisfy Hom-Jacobi identity,we have

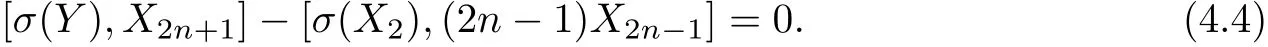
Since the second Lie bracket of equation(4.4)is zero,we have c0=0.It is a contradiction.

(3)Similarly,if c0=2 or c0/=01,2,we also get contradictions.

(4)If c0=1.We have a2=b1=0.Considering Y,X1,X2satisfy Hom-Jacobi identity,we have b4=b5=···=b2n?1=0.By equation(4.3),we get

That is,b3=b2n=0,c1b2=0,(2n?1)b2n+1?c2n?1b2=0.

If b2=0,we have b2n+1=0,that is,σ(X2)=0.Similar to case(2),it is a contradiction. Hence,we get

Since σ(Xi+1)=[σ(X1),σ(Xi)],we have

Considering Y,X1,Xj(2≤j≤2n)satisfy Hom-Jacobi identity,we have

Hence,we get

Since 2≤j≤2n,by equation(4.7),we have a1=b2=1.Equation(4.2)implies,

We have

By equations(4.8)and(4.9),we have a3=···=a2n?1=0,c2=···=c2n?2=0 and

Equation(4.10)implies 2na2n+1?c2n=0.Therefore,

In summary,we get the representation of σ

AcknowledgementThe authors are grateful to the referee for his valuable suggestions.

[1]LEVI E E.Sulla struttura dei gruppi f i niti e continui[J].Atti Accad Sci Torino,1905,40:551-65.

[2]HUMPHREYS J E.Introduction to Lie Algebras and Representation Theory[M].New York:Springer-Verlag, 1972.

[3]NDOGMO J C,WINTERNITZ P.Solvable Lie algebras with Abelian nilradicals[J].Journal of Physics A, 1994,27:405-423.

[4]RUBIN J,WINTERNITZ P.Solvable Lie algebras with Heisenberg ideals[J].Journal of Physics A,1993, 26:1123-1138.

[5]TREMBLAY S,WINTERNITZ P.Solvable Lie algebras with triangular nilradicals[J].Journal of Physics A,1998,31:789-806.

[6]WANG Yan,LIN Jie,DENG Shao-qiang.Solvable Lie algebras with quasif i liform nilradicals[J].Communication in Algebra,2008,36:4052-4067.

[7]HARTWIG J T,LARSSON D,SILVESTROV S D.Deformations of Lie algebras using σ-derivations[J]. Journal of Algebra,2006,295:314-361.

[8]JIN Quan-qin,LI Xiao-chao.Hom-Lie algebra structures on semi-simple Lie algebras[J].Journal of Algebra, 2008,319:1398-1408.

tion:17B05,17B30

CLC number:O152.5Document code:A

1002–0462(2014)02–0231–07

date:2012-08-17

Supported by the National Natural Science Foundation of China(11071187);Supported by the Natural Science Foundation of Henan Province(13A110785)

Biography:LI Xiao-chao(1981-),male,native of Zhumadian,Henan,an associate professor of Huanghuai University,Ph.D.,engages in Lie algebra.