Combined algorithm of acquisition and anti-jamming based on SFT
Ying Ma,Xiangyuan Bu,Hangcheng Han,and Qiaoxian Gong
School of Information and Electronics,Beijing Institute of Technology,Beijing 100081,China
Combined algorithm of acquisition and anti-jamming based on SFT
Ying Ma,Xiangyuan Bu*,Hangcheng Han,and Qiaoxian Gong
School of Information and Electronics,Beijing Institute of Technology,Beijing 100081,China
A communication and navigation receiver is required to remove hostile jamming signals and synchronize receiving signals effectively especially for satellite communication and navigation whose resources are becoming more and more limited.This paper proposes a novel signal receiving method by combining the processes of anti-jamming and synchronization to reduce the overall computational complexity at the expense of slightly affecting the detection probability,which is analyzed in detail by derivations. Furthermore,this paper introduces sparse Fourier transformation (SFT)into the proposed algorithm to replace fast Fourier transformation(FFT)so as to further reduce the calculation time especially in large frequency offset environments.
acquisition,anti-jamming,navigation,sparse Fourier transformation(SFT).
1.Introduction
In satellite communicationand navigationsystems,limited resources become an increasingly serious problem.For example,some inter-satellites’Doppler frequency shifts (DFSs)can be±500 kHz[1–3].The quick estimation of such high DFSs will bring a big challenge to the limited resources.Many other satellite systems such as the low earth orbit(LEO)to ground links,Ka-band communication between the lunar relay satellite(LRS)and the earthbased ground system(EBGS)in NASA’s lunar communication and navigation architecture[4]also face the same problem.It is very important for us tond fast algorithms for satellite receivers to reduce the resource consumption.Acquisition is a time-consuming process which performs a two-dimension search to estimate the code phases and DFSs of satellite signals.Common traditional acquisition algorithms mainly include correlator-based,matchlter-based and FFT-based algorithms[5–11].Their heavy computation burden consequently leads to large power consumption and millions of hardware multiplications[12–13].Thus all the algorithms mentioned above, eventhe fastest FFT-based algorithm,will impose great restrictions on their applications[14].What’s more,highpower jamming is increasingly becoming a potential problem for satellite based communication,especially for satellite-ground links which are widely used in earth observation and navigation.Reference[15]shows that the electromagnetic interference to ultra high frequency (UHF)band signals of LEO-groundlinks is mainly narrow band inference,including single tone jamming,multi-tone jamming,continuous pulse wave interference and other possiblenarrow-bandinterference.Facedwith such a complicated environment mentioned above,how to reduce the jamming inuence is becoming another important problem.Hence,an improved acquisition method which has a stronger anti-jamming ability and less computation complexity is proposed.
The contributions of this paper can be summarized as follows:
(i)Firstly,we introduce anti-jamming into the FFT-based acquisition algorithm.Traditionally,an interference excision block has to be located before the acquisition block in strong interference environments[16,17].Considering the huge overlap between these two blocks,we propose a combined method for fast and reliable signal receiving.
(ii)Secondly,we analyze the impacts of interference on acquisition probabilityusing theoretical derivationsand simulations.
(iii)Thirdly,to further reduce the computation complexity,we introduce sparse Fourier transformation(SFT), presented in 2012 by Haitham Hassanieh[18,19],into our method.They used the simplied SFT to modify the traditional FFT-based acquisition[20].However,their methodcannotworkverywellunderlargefrequencyoffsetandlow signal-to-noiseratio(SNR)situationsbecausethe powerof the input satellite signal will be decreased if it is subsampled in the frequency domain to reduce the whole computation complexity.Moreover,it is not easy to be combined with the interference suppression block.Therefore,in this paper,we improve this method and introduce it into our combined algorithm to replace inverse fast Fourier transform(IFFT)when we compute the correlation.Our proposedmethodreducesthecomputationcomplexityofIFFT from O(N log(N))to O(r(W+B logB+|C|))(N is the point number of the input of the IFFT,r,B,W,C are parameters of SFT which will be described later).Meanwhile,its performance is as good as the traditional FFT-based method in strong interference and high dynamic environments.
This research work is organized as follows.Section 2 presents system descriptions.Section 3 analyzes the performance.Section 4 introduces the SFT algorithm.In Section 5,simulations are performed and the results are presented.Conclusions are driven in Section 6.
2.System description
A direct sequence spread spectrum(DSSS)system is considered in our work,which usually contains three primary signal processing blocks in baseband,arranged serially: signal acquisition module,tracking module and data decoding module.A signal acquisition module is responsiblefordetectingreceivingsignals,estimatinginitial phases of the pseudo-random binary sequence(PRN)and DFS of signals.A fast and reliable acquisition block is the premise and basis for the next two blocks.However,although the DSSS system has certain ability of anti-jamming,it still cannot work very well if the interference is too strong to suppress.Hence,we always put an interference excision block before acquisition.In order to reduce the computation complexity,this paper proposes a combinedalgorithm of anti-jamming and acquisition based on SFT.Some parameters are dened in Table 1,and the new algorithm is depicted in Fig.1.

Table 1 Parameter defnition

Fig.1 Block diagram for the combined acquisition and antijamming algorithm
First,the incoming signal can be expressed as

where s(t),j(t),and n(t)denote respectively the signal, the narrow-band interference and the noise which is a additive white Gaussian noise of zero mean and two-sided power spectral density N0/2.As shown in[21],without loss of generality,the system adopts a BPSK modulation scheme,so the input signal at the nth sample,can be expressed as

where d(nTs)={?1,1}is the data bit stream,P(nTs) is the spreading code which is the±1 valued PRN code. Without loss of generality,the interference is assumed to be a narrow-bandsignal whose central frequencyis ωIF.It is expressed in the frequency domain as

where ωaand ωbare frequencies near ωIF.The in-phase and quadrature signals after down conversion are rI(nTs) and rQ(nTs),i.e.

Then,in orderto excisethe interference,the inputsignal is transformed into the frequency domain by FFT for each block of N samples which is given by

where k=0,1,...,N?1,xT(n)=x(t)t=nTs.

where tnis the delay caused by convolutionwith the bandstoplter.
We use Taylor series to approximate hbs(t)and cut it with a rectangularwindowto makeit physicallyrealizable. Therefore,

Accordingto the convolutiontheorem,multiplyinga bandstoplter Hbs(ω)in the frequency domain is equivalent to convolving with hbs(t)in the time domain.After the antijamming block,the receiving signals become

with?denoting convolution and



After that,the non-coherent detector will evaluate the powerand judge whether it passes the preset threshold.If it does,the signal is successfully captured.Otherwise,the synchronizing process above will be repeated for all the other possibleuntil the correlation peak exceeds the acquisition threshold.Hereis the step size of the estimated frequency,M is a positive integer.If the frequencyoffset is verylarge,we will adopt parallel acquisition in the frequency domain shown in Fig.1.
Finally,in order to reduce the computation complexity, we use FFT and IFFT to replace the correlation in(10)according to the convolution theorem,i.e.


We use F(x(n))to denote the Fourier transformation of x(n),and F?(x(n))to denote the conjugate of F(x(n)) in this paper.As we all know,the maximum number of frequencies we have to search is decided by the maximum frequencyoffset.Hence,if thefrequencyoffsetis toolarge, there will be too many FFT and IFFT points to compute, which will impose great restrictions on their applications. To reduce the computation complexity,we use the cyclic shifts for the FFTs of the initial ωdto replace the computation of all the FFTs for all the other ωd.
3.Performance analysis
We start with the derivation of the correlation output:eIand eQ.As eIand eQhave similar expressions,we will analyze the in-phase component eIas an example.Then we will analyze the detection probability of our combined algorithm.
3.1Outputs of correlation
The“integration and dumping”function described above is equivalent to a low pass(LP)lter with an unit-impulse response in time and frequency domains,i.e.

As a result,only the difference frequencycomponentΔωdneeds to be considered,here Δωd=?ωd?ωd.At the output of the“integration and dumping”lter,we dene I as the in-phase component of the signal,NIas the in-phase component of the noise,Q is the quadrature component of the signal,NQis the quadrature component of the noise, i.e.

Based on(10),we get


and

Let

Assuming that the code delay between the input PRN code and the local PRN code is

then,

where l is an integer and|ρ|<1.
According to[22–24],we get


Let

When the PRN code phase is captured,i.e.l=0 and

then,
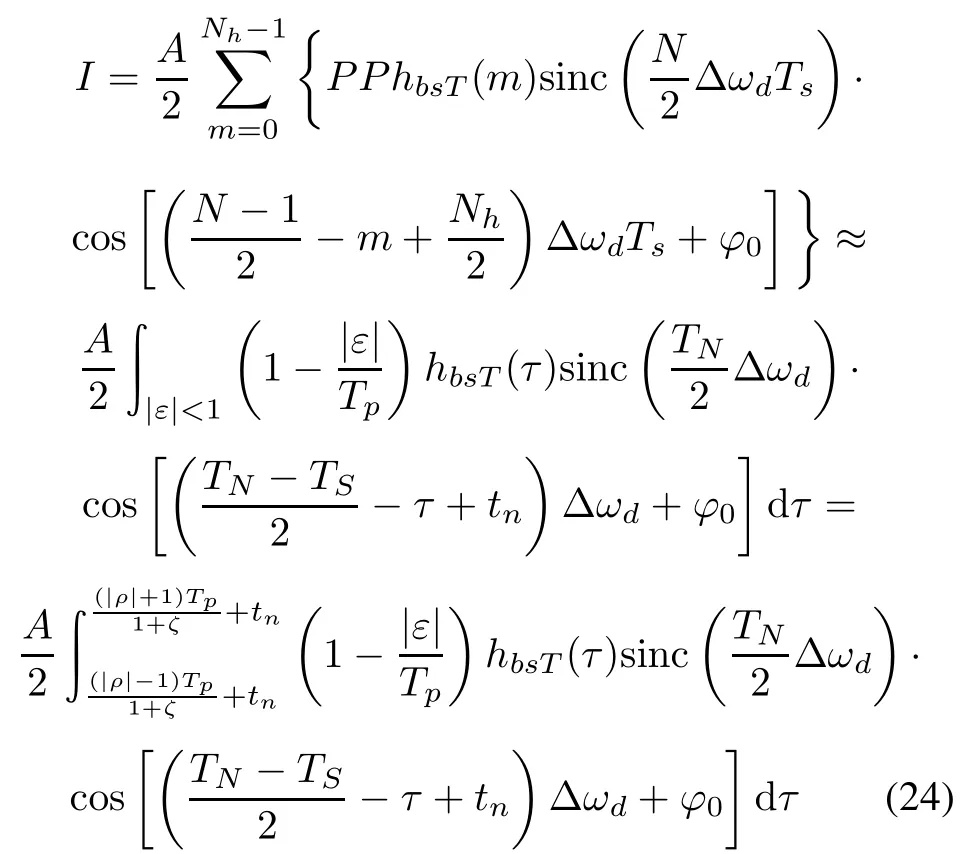
where TN=NTs.
Whenthe jammingsignal’s bandwidthis zero,the bandstoplterwill beanall-passlter,i.e.BBS=ωb?ωa=0, then hbs(t)=δ(t?tn).We get
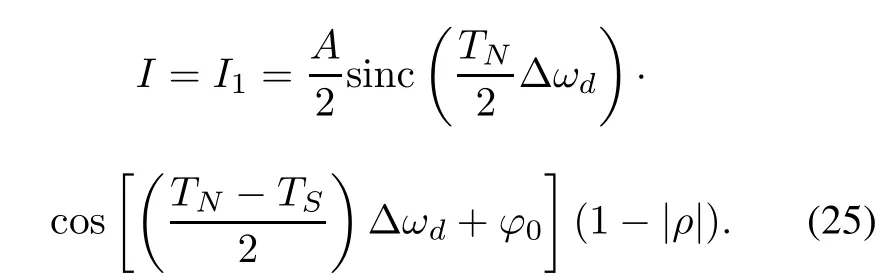
Otherwise,

where


Based on(26)and(27),we have

Then we will focus on the analysis of the noise component NI.According to(14),NIis related to the noise nT(n).Specically,nT(n)is the sampled white Gaussian noise,whosebandwidthisapproximatelyequivalenttothat of the PRN code which is 1/NTs.As the noise is independent of the local PRN code,the effect of convoluting with the local PRN code is to spread the power density of the noise over a bandwidth wider than its original bandwidth and thereby reduce the power spectral density over the bandwidth of the“integration and dumping”function. Therefore,NIis a zero-mean Gaussian whose variance is N0/(2N)[22].Similarly,the quadrature component is eQ=Q+NQ,here

and

3.2Detection probability analysis
Inthissection,we will discusstheacquisitionproblem.Let

then we get

whose expectations and variances are


As eIand eQare approximately independent,the joint probability density of eIand eQbecomes


and

where I0(x)is the modied Bessel function of zero order. If the detection threshold is set as ν,then the detection probability becomes


and

In this situation,the detection probability becomes

It can be perceivedthat the simulation result(see farther below)is found to be in good agreement with our theoretical derivation shown above.
4.SFT application
Although the well-known Fourier transformation has been deeplyinvestigatedin navigationsystems nowadays,many inter-satellite links which have high DFSs are still constrained by resources.It is necessary for us to investigate a new algorithm which can ease resource burden for future satellite communication and navigation systems.SFT has recently drawn much attention because it can compute the FFT/IFFT of a sparse signal in sublinear time.It was proved in[18]that the Fourier coefcients computed by SFT satisfywith probability 1?1/n,here x is the FFT of the input signal,n is the length of x,is the SFT of the input signal,x?Scontains the values of the small Fourier coefcients,k is the number of the large coefcients,ε and δ are thelter parameters which will be dened later.From this inequality we can observe that if the output of FFT is sparse,we can use SFT to replace FFT.The more sparse of the Fourier coefcients of the signal are,the less error caused by SFT will be introduced.
According to(5),the output of IFFT is very sparse as shownin Fig.2(a).The largecoefcientsrepresentthe correlative peaks and the leakage of correlative peaks caused by thelter.Evidently,it satises the restricted condition of the input signal of SFT(sparsity).Hence,we use SFTto replaceIFFT to reducethe whole computingcomplexity in the acquisition block.The whole acquisition process is shown in Fig.2.Instead of estimating all the Fourier coefcients of the output of IFFT,this algorithm onlynds and estimates the relatively large ones(such as point 39 to point 43 in Fig.2(a)),and then picks out the largest one which represents the position of ξ and ωdthat we search for.It is easy tond out that the largest value is obtained at point 41.

Fig.2 Correlation peak estimating process using SFT
To make it simpler,we assume that the length of the input data of SFT is 80 points,although the real data length is farmorethan 80.To bespecic,it works[18]as follows:

where x is the input of SFT.
Step1Permutex(n)witharandomκandλ(κ,λ∈[n] with λ odd),i.e.

Step 2Dene y′=Gy.Here G denotes thelter used in Fig.2(c)which is an ideal box-carlter of length 6 in the frequency domain.Thislter can also be obtained by convolving a Dolph-Chebyshev function with a box-car function.Deneat window G(ε,ε′,δ,W)as: supp(G)?[?W/2,W/2],F(G)i∈[1?δ,1+δ]for all i∈[?ε′n,?ε′n]and F(G)i<δ for all i/∈[?εn,?εn] [18].It has been proved that,in the frequency domain,this efcientlter G is nearlyat inside the pass region and has an exponential tail outside.After that,the spectrum of y around the large coordinates becomes large as shown in Fig.2(c)markedinreddashedrectangles.Onlyinthisway, the downsampling coordinates in the next step which are the nearest to the large coordinates in the permuted spectrum can be large.


whose elements are the coordinates near the coordinates in J.As a result,set E is likely to contain large coefcients. We can compute F(zi)in O(W+B log2B)time,considering multiplication bylter G in Step 2.In this example, set E contains 12 elements.As we can see not all the 12 elements in E are the real large coefcients.
Step 4Find the locations of the elements in set E in the original spectrum,i.e.C={i∈[n]|κi∈E}(It takes time of O(|C|)).However,we still cannot identify the real large coefcients in set C before Step 5,shown with big points in Fig.2(e).The real large coefcients are marked red,and the false large coefcients caused by leakage and downsampling are marked blue.
Step 5For r∈{1,...,L}(here L is 3),we perform Steps 2,3,4 for r times to get Cr.For each i∈C= C1∪···∪CL,let

where s denotes the score every coordinate obtained in the original spectrum.As the permutationin Step 1 is random, only the real large coefcients can most likely exist in C′because of the high scores they get.Even a minority ofwrong positions can be omitted because the value of F(x) is estimated as the median one,

As shown in Fig.2(f),the highest scores are s(40),s(41), s(42),which correspond to the largest three coordinates in Fig.2(a).In this way,the total running time is reduced to O(r(W+B log2B+|C|)).Moreover,it can work very well in environments of large frequency offset and low SNR,which will be shown in Section 5.
Compared with[18],we omit the pre-processing.The purpose of pre-processing is to restrict the positions of the large coefcients to a set to reduce the computation complexity.It works as follows.

Then,in Step 5,after obtaining Ci,every element in Cishouldbe checkedwhetherit belongsto A.If not,it will be removedout of Ci.Hence,set Ciwill have fewer elements and the whole computation complexity will be reduced.
However,this process is not required in acquisition.Because the number of large coefcients is very small,the number of elements in Ciis also small.We do not need to reduce the number of elements in Cianymore.Moreover, the cost of preprocessingwill increase the whole complexity.As a result,we decide to remove this process to reduce the whole complexity.
Reference[20]aliases the inputsignal and computesthe FFT of the aliased signal to obtain the subsampled Fourier coefcients of it.And then,it does the same operation to the local PRN code to obtain the subsampled Fourier coefcients of the local PRN code.Finally it times the subsampled Fourier coefcients of the input signal and the subsampled Fourier coefcients of the local PRN code and transforming the result into time domain tond the correlation peak.Compared to[20],we make two changes.
Firstly,the method in[20]can only obtain the subsampled Fourier coefcients of the input signal,however,if there are narrow-bandinterference signals mixed in the input signal,the performance will be very bad.As an improvement,we use FFT to obtain the spectrum of the input signal.In this way,we can easilynd the positions of the interferencefrequenciesandeliminate the interferencesignalbyan interferenceexcisionblock.TheSFT will beonly used in the IFFT process.
Secondly,[20]does not have the iteration process such as Step 5.Moreover,the subsampled signal in[20]will lose much frequencyinformation.Hence,this method cannot be used in low-SNR environments.As an improvement,we make iterations in Step 5 to improve the location accuracy.
5.Performance simulations
In order to evaluate the performanceof our new algorithm, we carried out three simulations.The parameters are set as Table 2.

Table 2 Values of parameters in the simulations
Each point shown in simulations below is the average over 100 runs with different realizations of code phasedelays and noises randomly chosen.
Firstly,in order to verify the theoretical derivations of the acquisition probability in Section 3,both theoretical and simulation results are plotted in Fig.3.As we can see, the acquisition probability is found to be in good agreement with our theoretical prediction.

Fig.3 Acquisition probability of the theoretical value and simulation value
Secondly,we analyze the impacts of narrow-band interferences on acquisition probability.In our experiments, wex the bandwidth of the interference as 20 kHz and report the acquisition probability with different jamming-to-signal power ratios(JSRs):15 dB,20 dB,24 dB,27 dB.As we can see from Fig.4,the traditional receiver cannot work very well as the interference gets strong.Nevertheless,in our new algorithm which combines the interference excision with the acquisition block, the signal can be captured accurately if SNR>?15 dB.

Fig.4 Acquisition probability with different jamming signals
Thirdly,we evaluate and compare the performances of FFT and SFT in the acquisition block under a large frequency offset(500 kHz).In most cases,the acquisition probability is required to be 99%or even more,otherwise, it will become meaningless.As we can see in Fig.5,when SNR>?15 dB,there is no difference between the acquisition accuracies of FFT and SFT,which remain to be nearly 100%.Thus,we can come to the conclusionthat the reduced runtime does not come at the expense of performance losses.

Fig.5 Acquisition probability of FFT and SFT
6.Conclusions
This paper presents a combinedalgorithmof anti-jamming and synchronization based on SFT for satellite based communication and navigation receivers.Both theoretical derivations and simulations for detecting probability are carried out in this paper.They demonstrate that our new algorithm can not only work very well in strong interference environments but also largely reduce the computing complexity while slightly affecting the acquisition accuracy.Furthermore,we believe that the sparse Fourier transformation will play a greater role in other kinds of interference excisions besides the narrow-band ones.These achievements have not been achieved in the literature till date to the best of our knowledge.Also,we plan to explore different applications in our future work.
[1]S.Amiri,M.Mehdipour.Accurate doppler frequency shift estimation for any satellite orbit.Proc.of the 3rd International Conference on Recent Advances in Space Technologies,2007: 602–607.
[2]Y.Xu,Q.Chang.A tracking method for weak and high dynamic GNSS inter-satellite link signal.Proc.of the 2nd International Conference on Communications and Networks,2012: 111–114.
[3]J.S.Chern,Z.C.Hong.Design and application of intersatellite link in weather observation constellation.Journal of Marine Science and Technology,2012,20(4):472–477.
[4]V.Badescu.Moon: Prospective energy and material resources.New York:Springer Verlag,2012.
[5]E.D.Kaplan.Understanding GPS principle and applications. Norwood:Artech House,1996.
[6]D.J.R.van Nee,A.J.R.M.Coenen.New fast GPS code acquisition technique using FFT.Electronics Letters,1991, 27(2):158–160.
[7]A.J.R.M.Coenen,D.J.R.van Nee.Novel fast GPS/GLONASS code-acquisition technique using low update rate FFT.Electronics Letters,1992,28(9):863–865.
[8]H.S.Seo,C.Park,S.J.Lee.A new fast acquisition algorithm for GPS receiver.http://cslab.cnu.ac.kr.
[9]Z.Zhu.Averaging correlation for weak GPS signal processing. Ohio:Ohio University,2002.
[10]B.Buchli,F.Sutton.GPS-equipped wireless sensor network node for high-accuracy positioning applications.Proc.of the 9th European Conference on Wireless Sensor Networks,2012: 159–179.
[11]R.J.L.M.Sahmoudi,M.G.Amin.Acquisition ofweak GNSS signals using a new block averaging pre-processing.Proc.of the Conference on Position,Location and Navigation Symposium,2008:1362–1372.
[12]OriginGPS. ORG447X series datasheet. http://w-ww. acaltechnology.com.
[13]Perthold Engineering LLC.SkyTraq venus 6 GPS module. http://www.perthold.de.
[14]A.C.Team.Fundamentals of global positioning system receivers:a software approach.New Jersy:John Wiley&Sons, 2005.
[15]J.Y.Liang.Studying on narrowband interference suppression inLEO satellitespread spectrum communication systems. Shanghai:Shanghai Institute of Microsystem and Information Technology,2006
[16]L.B.Milstein,P.K.Das.An analysis of a realtime transform domainltering digital communication system—Part I: narrow-band interference rejection.IEEE Trans.on Communi-cations,1980,28(2):816–824.
[17]S.Davidovici,E.G.Kanterakis.Narrowband interference rejection using real-time fourier transforms.IEEE Trans.on Communications,1989,37(7):713–722.
[18]H.Hassanieh,P.Indyk,D.Katabi,et al.Simple and practical algorithm for sparse Fourier transform.SODA,2012:1183–1194.
[19]H.Hassanieh,F.Adib,D.Katabi,et al.Nearly optimal sparse fourier transform.Proc.of the 44th ACM Symposium on Theory of Computing,2012:563–578.
[20]H.Hassanieh,P.Indyk,D.Katabi,et al.Faster GPS via the sparse Fourier transform.Proc.of the 18th Annual International Conference on Mobile Computing and Networking, 2012:353–364.
[21]W.Zhuang,J.Tranquilla.Modeling and analysis for the GPS pseudo-range observable.IEEE Trans.on Aerospace and Electronic Systems,1995,31(2):739–751.
[22]W.Zhuang.Composite GPS receiver modeling,simulations and applications.University of New Brunswick,1992.
[23]W.J.Gill,J.Spilker.An interesting decomposition property for the self-products of random or pseudorandom binary sequences.IEEE Trans.on Communications Systems,1963, 11(2):246–247.
[24]A.Polydoros,N.B.Pronios.On the power density of digital modulated signals and applications in code dispreading.Proc. of the 21st Conference on Century Military Communications, 1988:977–981.
Biographies

Ying Ma was born in 1989.She is currently working towards her Ph.D.degree with Beijing Institution of Technology.Her research interests are energy-efcient optimization,GPS navigation, and sparse Fourier transformation.
E-mail:mayingbit2011@gmail.com

Xiangyuan Bu was born in 1965.He is a professor in Wireless Communications and Networks Laboratory,School of Information and Electronics,Beijing Institute of Technology.His current research interests are wireless communication and signal processing.
E-mail:bxy@bit.edu.cn

Hangcheng Han was born in 1985.He is a lecturer in Laboratory for Modern Communication School of Information and Electronics,Beijing Institute of Technology.His current research interests are satellite communication and navigation,low SNR receiver,spread spectrum communications and antijamming technology.
E-mail:hanhangcheng@bit.edu.cn

Qiaoxian Gong was born in 1990.She is a master of information and communication engineering in School of Information and Electronics,Beijing Institution of Technology.Her current research interests are GPS navigation,signal processing,and earth-moon orbit navigation.
E-mail:chelcygong@gmail.com
10.1109/JSEE.2015.00050
Manuscript received April 01,2014.
*Corresponding author.
This work was supported by the National Natural Science Foundation of China(The Key Research of Beidou Receiver based on SFT, 61301089).
 Journal of Systems Engineering and Electronics2015年3期
Journal of Systems Engineering and Electronics2015年3期
- Journal of Systems Engineering and Electronics的其它文章
- Multi-channel differencing adaptive noise cancellation with multi-kernel method
- Modied sequential importance resamplinglter
- Immune particle swarm optimization of linear frequency modulation in acoustic communication
- Parameter estimation for rigid body after micro-Doppler removal based on L-statistics in the radar analysis
- Antenna geometry strategy with prior information for direction-nding MIMO radars
- Modied Omega-K algorithm for processing helicopter-borne frequency modulated continuous waveform rotating synthetic aperture radar data
