Resultant matrices and Bezoutians under the polynomial bases generated by a bilinear transformation function
WU Hua-zhang
(School of Mathematical Sciences, Anhui University, Hefei 230601, China)
?
Resultant matrices and Bezoutians under the polynomial bases generated by a bilinear transformation function
WU Hua-zhang
(School of Mathematical Sciences, Anhui University, Hefei 230601, China)
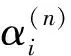
bilinear transformation function; companion matrix; resultant matrix; Bezout matrix; Barnett’s formula
0 Introduction
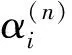
whichestablishatransformationbetweentheupperhalfandthelowerhalfcomplexplanes.Ontheotherhand,thematrixcorrespondingtothebilineartransformationfunctionaboveisaMobiustransformationmatrixwhichcanbeusedtoestablishaone-to-onecorrespondencebetweenHankelandToeplitzmatrices[5].
Itiswellknown[6]thatthereexistcloserelationsbetweenresultantmatrixandBezoutmatrix(orsimplyBezoutian).TheBezoutianshavemanyimportantapplicationsinnumericalcomputing,controltheory,systemidentification,andnetworksandsignalprocessing.WerefertothebooksofBarnett[7],LancasterandTismenetsky[8],andBiniandPan[9].AmongthemethodsforthestudyofBezoutiansthepowerbasisisusuallygeneralizedtopolynomialcases.Ithasbeenshownin[10-11]thatmostpropertiesofclassicalBezoutian,suchastheBarnett-typeformula,theintertwiningrelationandthediagonalreduction,keepstillthesimilarformsforsomegeneralizedpolynomialBezoutians.
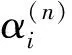
1 Resultant matrices
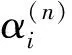
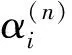
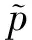
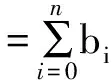
Thus, E-1Acanberegardedasacompanionmatrixofp(λ).Thepurposeofconstructingsuchacompanionmatrixismainlyfortheconvenienceofthecomputationoftheelements,notmerelyforitstheoreticalapplications.
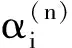
whichimplies
(1)
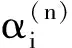
Nowweconsidertheresultantmatrixoftwopolynomials.Set
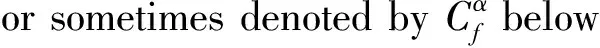
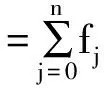
(1) g(Cα)isaresultantmatrixoff(z)andg(z).
(2)ThedegreeoftheGCDd(z)off(z)andg(z)isequalton-rank(g(Cα)).
(3)Thecoefficientsofd(z)areproportionaltothelastrowofg(Cα)afterbeingreducedtorowechelonform.
Forexample,let
Thenthecompanionmatrixoff(x)is
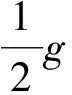
thus rank (g(Cα))=1, and the degree of the GCD off(x) andg(x) is equal to 3-1=2. According to Theorem 1(3),d(x) should be proportional to
which is equal tog(x).
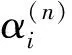
can be determined by
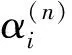
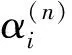
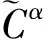
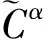
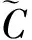
2 Bezoutians
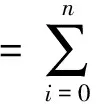
(2)
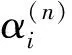
For the computation of the elements of generalized Bezoutian, by [15] we have following formulas and ommit its proof. Here we still distinguish two different bases.
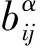
Thus the cost of the algorithm iso(n2).
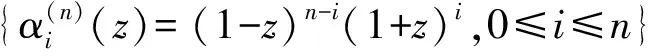
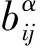
Thus the cost of the algorithm iso(n2).
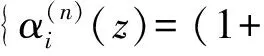
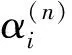
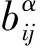
Thus, by the definition (2), the last equality equals
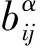
3 Properties and relationships of resultant matrices and Bezoutians
3.1 Properties of resultant matrices
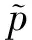
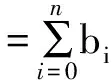
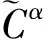
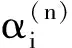
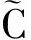
respectively,alsokeepthesimilarrelationshipswiththeirtransposes.
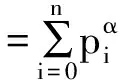
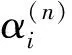
Theorem 6 Assume that notations are as above. Then the following relations are satisfied
(3)
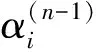
(4)
Proof Eqs.(3) can be checked by using a similar method as that in [15]. Here we omit the proof.
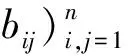
Theorem 7 Assume that notations are as before. Then we have
3.2 Relationships between Bezoutians and resultant matrices
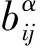
which implies
(5)
By those equalities we can generalize the Barnett’s formula
to a general form. SinceB(p,1) is a special Bezout matrix withq(z)=1, then
Thus, Eq.(5) implies
(6)
Theorem 8 Assume that notations are as before. Then the generalized Barnett’s formulas hold
ThegeneralizedBarnett’sformulasaboveimplythefollowingresult.
Corollary 3 Assume that notations are as before andJthe reverse unit matrix. Then
Proof We only verify the first equality, the second one can be similarly proved and omitted. In view of Prop.2.11 in [5], we have
whereCpdenotes the companion matrix ofp(z), andJis the reverse unit matrix. Multipling byBTandBfrom the left hand side and the right hand side on the last equality respectively, and using Eqs.(3) and (5), we have
whereJα=BJBT.Theproofiscompleted.
AnintertwiningrelationofthegeneralizedBezoutianswiththeresultantmatricesarefulfilled.
Theorem 9 Assume that notation are as before. Then we have
Proof We only prove the first equality. By [8], we have the following equality
Using Eqs.(3) and (5), the remain is merely some elementary calculation.
[1] Emiris I Z, Mourrain B. Matrices in elimination theory[J]. Symbolic Comput,1999,28(1/2):3-44.
[2] Kajiya J T. Ray tracing parametric patches[J]. Computer Graphics, 1982,16:245-254.
[3] Farouki R T, Goodman T N. On the optimal stability of the Bernstein basis[J]. Math Comp, 1996,65:1553-1566.
[4] Farouki R T, Rajan V T. On the numerical condition of polynomial in Bernstein form[J]. Comp Aided Geom Design, 1988,5:1-26.
[5] Heinig G, Rost K. Algebraic methods for Toeplitz-like matrices and operators[M].Basel:Birkhauser,1984.
[6] Barnett S, Lancaster P. Some properties of the Bezoutian for polynomial matrices[J]. Linear and Multilinear Algebra, 1980, 9:99-110.
[7] Barnett S. Polynomials and linear control system[M].NewYork:Marcel Dekker, 1983.
[8] Lancaster P, Tismenetsky M. The theory of matrices[M]. 2nd ed.London:Academic Press, 1985.
[9] Bini D A, Pan V. Numerical and algebraic computations with matrices and polynomials[M].Boston:Birkhauser,1994.
[10] Mani J, Hartwig R E. Generalized polynomial bases and the Bezoutian[J]. Linear Algebra and Its Applications, 1997,251:293-320.
[11] Wu H Z. More on polynomial Bezoutians with respect to a general basis[J]. Electronic Journal of Linear Algebra, 2010,21:154-171.
[12] Winkler J R. A companion matrix resultant for Bernstein polynomials[J]. Linear Algebra and Its Applications 2003,362:153-175.
[13] Golub G H, Van Loan C F. Matrix computations[M].Baltimore:John Hopkins University Press,1989.
[14] Montaudouin Y D, Yiller W. The Cayley method in computer aided geometric design[J]. Comp Aided Geom Design, 1984,1:309-326.
[15] Wu H Z, Sun J P. A generalized Bezout matrix under a special polynomial basis[J]. Journal of Hefei University:Natural Sciences, 2014,24(2):5-9.
(責(zé)任編輯 朱夜明)
雙線性變換函數(shù)生成基下的結(jié)式矩陣和Bezout矩陣
吳化璋
(安徽大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,安徽 合肥 230601)
雙線性變換函數(shù);友矩陣;結(jié)式矩陣;Bezout矩陣;Barnett公式
10.3969/j.issn.1000-2162.2015.06.001
Foundation item:Supported by the Natural Science Foundation of Anhui Province (1208085MA02)
O151 Document code:A Article ID:1000-2162(2015)06-0001-08
Received date:2015-02-16
Author’s brief:WU Hua-zhang (1966-), male, born in Quanjiao of Anhui Province, professor of Anhui University,tutor for postgraduate.

