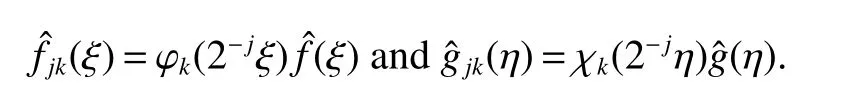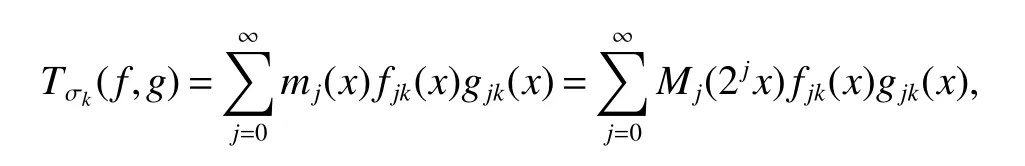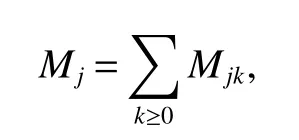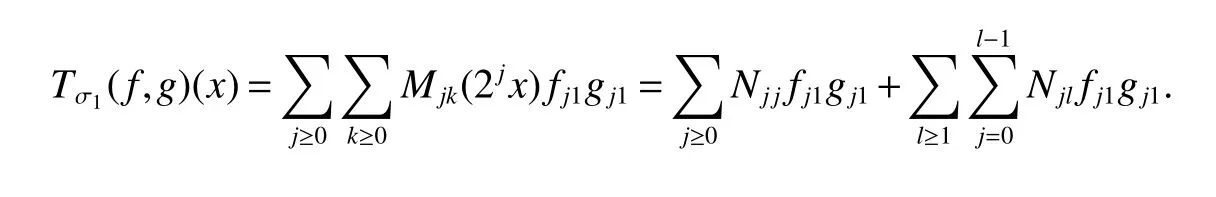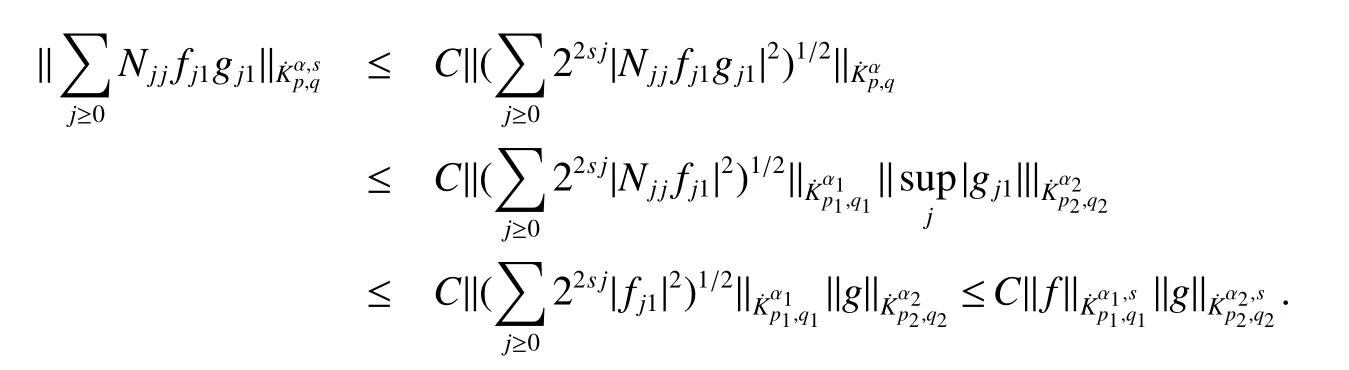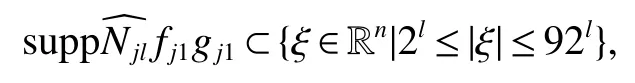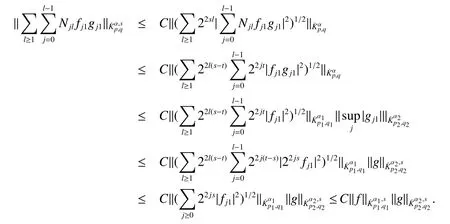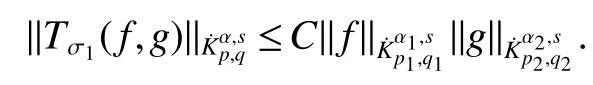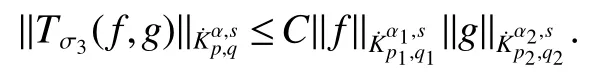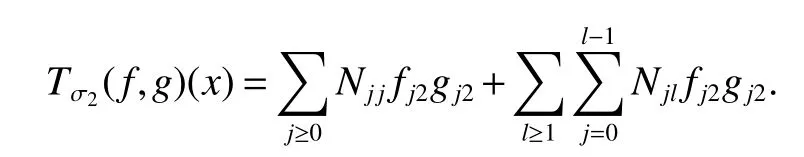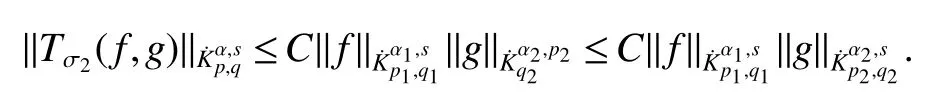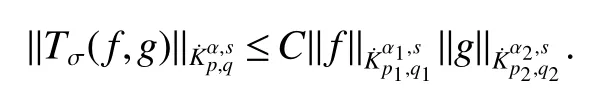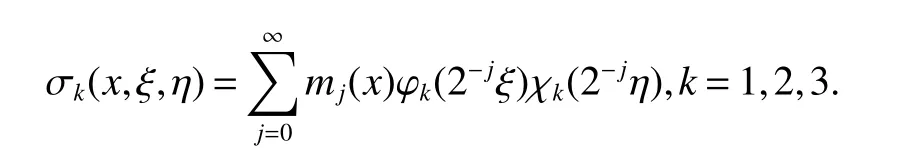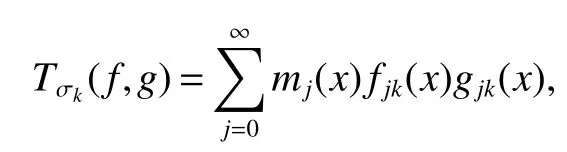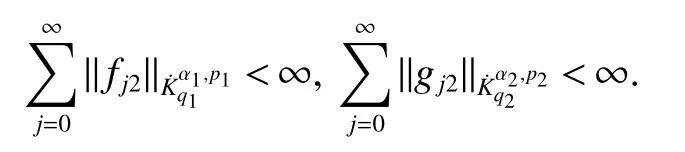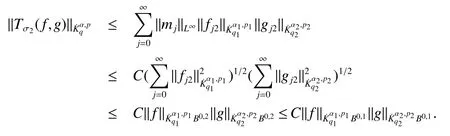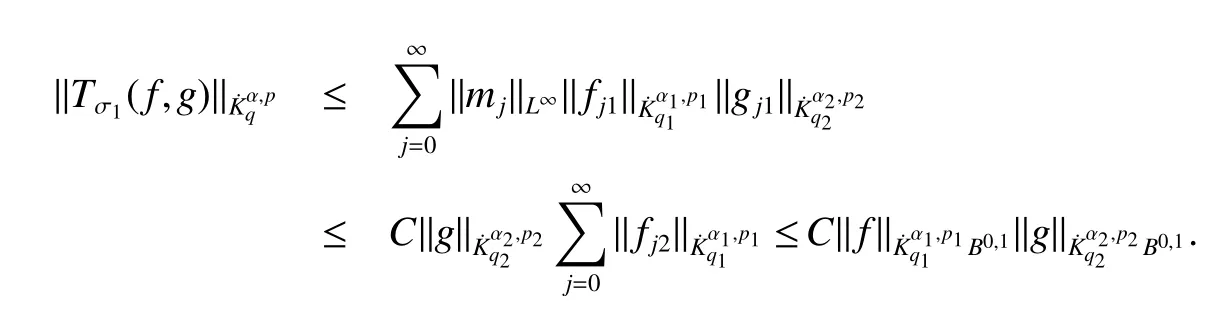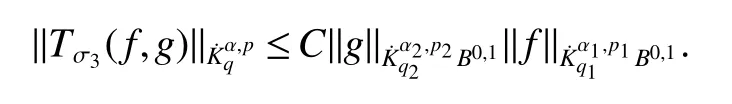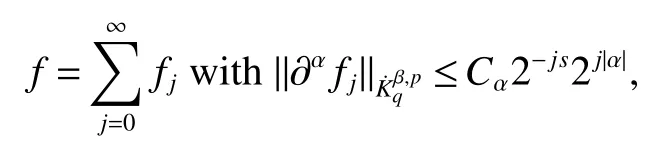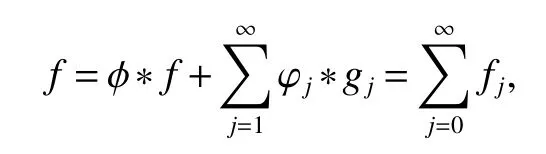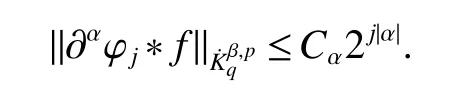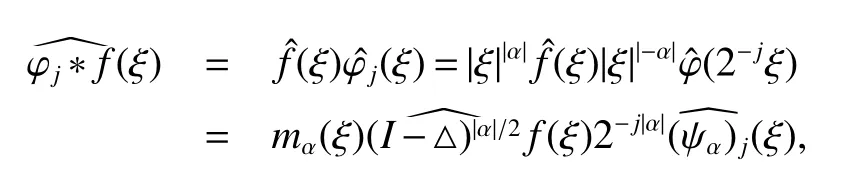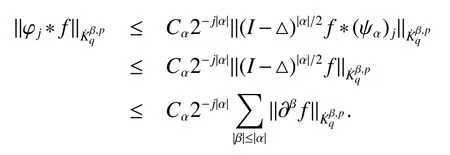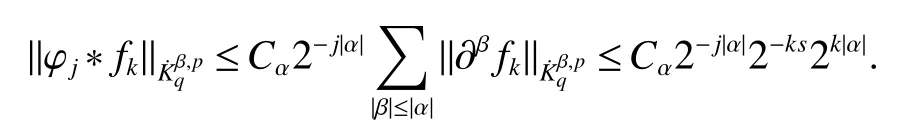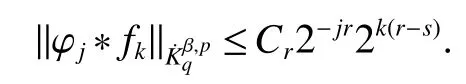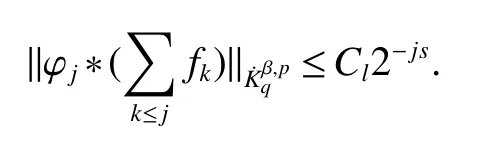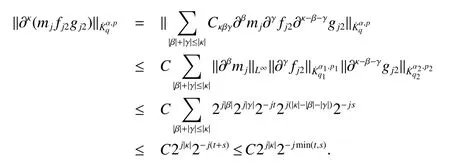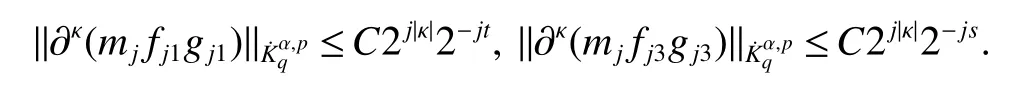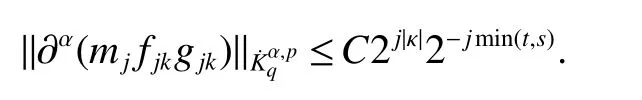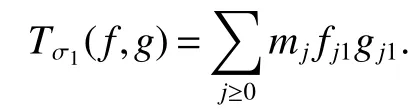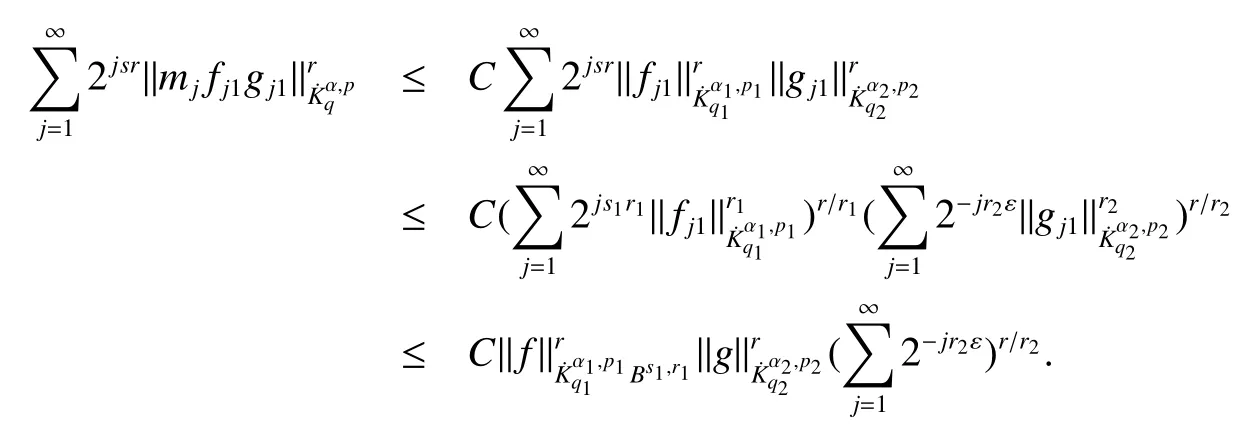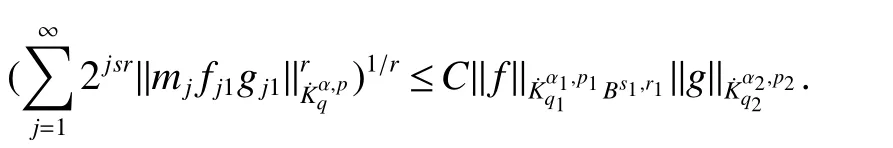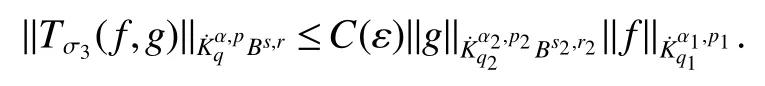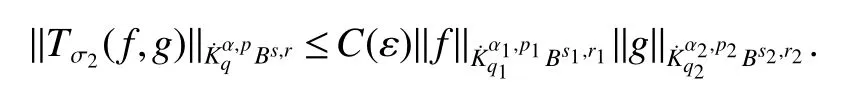Bilinear Pseudodifferential Operators with Forbidden Symbols on Herz Type Spaces?
CAO Yong-hui,YUAN Mao-qin,GOU Qian-qian
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: In this paper,using the powerful decomposition techniques related to Littlewood–Paley theory and time–frequency analysis,we prove that the bilinear pseudodifferential operators with forbidden symbols are bounded on products of Herz type Sobolev spaces and Herz type Besov spaces.
Key words:Herz space;Pseudo-differential operator;Forbidden symbol;Besov space
1 Introduction
The bilinear pseudodifferential operators are natural generalizations of the translation invariant bilinear operators.An important example is provided by the bilinear partial differential operators with the variable coefficientsIn this case,we haveL=Tσwith the symbol is given by
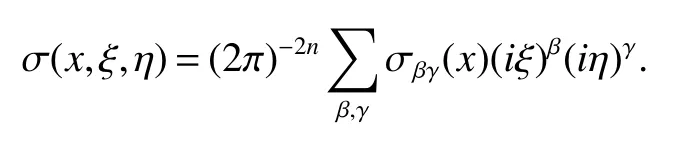
In what follows we propose the study of the boundedness properties of the class of bilinear pseudodifferential operators with the symbol inA symbol σ(x,ξ,η)is inif it satisfies estimates of the form
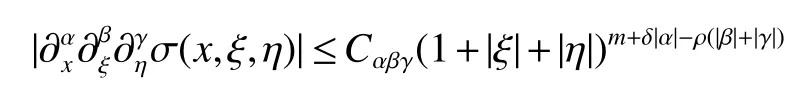
for all(x,ξ,η)∈R3n.If ρ=δ=1,we call this class symbols as forbidden class symbols.The bilinear pseudodifferential operatorTassociated with the symbol σ(x,ξ,η)is
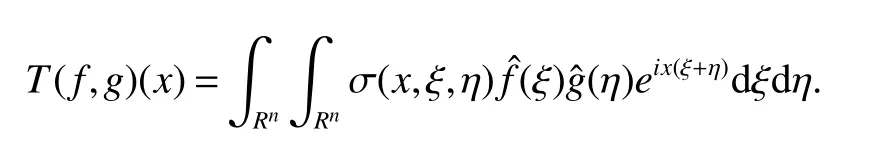
The definition of bilinear pseudodifferential operators can be seen in[1,2].
Bilinear pseudodifferential operators with forbidden symbols are known to be,in general,unbounded on products of Lebesgue spaces.A counterexample which disproves the boundedness fromL2×L2intoL1can be found in[3].It is then natural to ask whether there are any possible substitutes of Lebesgue spaces for which one can obtain the boundedness of this class of bilinear pseudodifferential operators.In[3],the authors have shown that if one replaces the Lebesgue spaces by Sobolev spaces with positive smoothness,then such boundedness holds.On products of Lipschitz and Besov spaces,in[1],the author show that bilinear pseudodifferential operators with symbols in the forbidden class are bounded.The purpose of this work is to prove that boundedness of the bilinear pseudodifferential operators with forbidden symbols also holds on products of Herz type Sobolev and Besov spaces.The results that we obtain give,in particular,the bilinear extensions of some theorems due to Bourdaud(see[4,5]),Bényi(see[1])and Stein(see[6]).In our proofs,we will employ the powerful decomposition techniques related to Littlewood–Paley theory and time–frequency analysis which were developed by Coifman and Meyer(see[7,8]).In Section 2,we show some of the notation and preliminaries employed in the subsequent section.The main results are stated and proved in Section3.
2 Notation and preliminaries
A bilinear operator,a priori defined on the product of Schwartz spaces S×S into the space of tempered distributions,via the symbol of the operator,can be realized(at least formally)in pseudodifferential form,
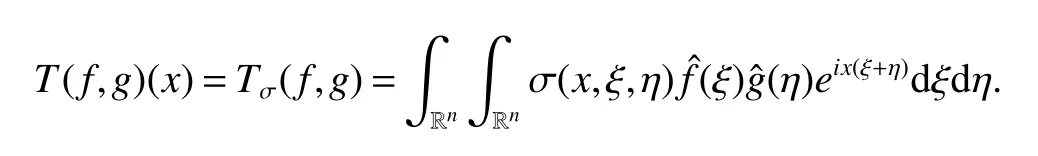
If σ(x,ξ,η)=1,the operator is the product of two functions.Another relevant example is provided by the bilinear differential operators with variable coefficients,see[2].For any three real numbersm,ρ and δ,we denote byBS mρ,δ the class with symbols satisfying following estimate

for all(x,ξ,η)∈R3n.Ifm=0,δ=ρ =1,we call σ∈BS01,1 a forbidden symbol or exotic symbols.These definitions can be seen in[1,2].
When we study the problem about pseudodifferential operators,an important method is that one can reduce the problem to the study of pseudodifferential operators with elementary bilinear symbols.This method is used firstly by Coifman and Meyer(see[7,8]).Using the idea of[7],we can write general symbol σ(x,ξ,η)as a sum of elementary symbols,where elementary symbol have the following form

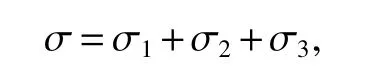
Now we give the definitions about Herz space and Herz type Sobolev and Besov spaces.
Definition 1Suppose?∞<α<∞,0 With the usual modification should be made whenp=∞orq=∞(see[9]). Definition 2Fors,α∈R,0 In order to define Herz type Triebel and Besov spaces,we need the following Littlewood-Paley function. Definition 3Let Φ be the collection of all systemsof real-valued even function with respect to the origin,such that φj(x)=φj(?x)ifx∈suppφjwhere for every multi-index α,there exists a positive numbercαsuch that and Now let us introduce Herz type Triebel space and Herz type Besov space(see[10]). Definition 4Let?∞ and In this section,we state our main results and give their proofs.Firstly,we give the result about Herz type Sobolev space. Theorem 1Every bilinear pseudodifferential operator with a symbol inhas a bounded extension fromwhere α1+α2=α,1/p1+1/p2=1/p,1/q1+1/q2=1/q,ands>0. ProofFirstly,we can assume our symbol to be elementary symbol.Let We can writeTσ(f,g)=Tσ1(f,g)+Tσ2(f,g)+Tσ3(f,g).Fork=1,2,3, where functionMjhave the propertyThe Littlewood-Paley decomposition ofMjis Now, Fors>0,we have In the estimates above,we used Littlewood-Paley characterization ofSimilarly,is supported in an annulus of size 2k.More precisely, where we use the the condition on the supports ofandSo we can write From these estimates,it follows that Similarly, In order to estimateTσ2,we decompose again have Due to the symmetry of the roles played byfj2andgj2,we also have From these estimates,we finally deduce that Now we give some results about Herz type Besov spaces. Theorem 2Let σ be a bilinear symbol in the forbidden classthenTσcan be extended as a bounded operator ProofIt is enough to restrict our attention to elementary bilinear symbols,σ=σ1+σ2+σ3,where The functionsmj,?kand χksatisfy the same conditions with the proof of Theorem 1.Forf,g∈S,we can writeTσ(f,g)=Tσ1(f,g)+Tσ2(f,g)+Tσ3(f,g).Fork=1,2,3, where We first prove(1)of Theorem 2. So we have ForTσ1,we have ForTσ3,we also have the same estimate, We complete the proof. In order to prove(2)of Theorem 2,we need the following lemma.It is a useful characterization of the spacesin terms of approximations by smooth functions. Lemma 1A functionfbelongs to,1 for all 0≤|α|≤l,lis the smallest integer strictly larger thans. ProofFirstly,we assume that,φ and ?jare Littlewood-Paley functions.So we have wheregj=(?j?1+?j+?j+1)?f.Using this form and condition ofit is clearly thatNote that ?j?fis union bounded formas an immediate consequence,we also have Conversely,we will show thatThis in turn will prove thatby using the fact that ? is a Littlewood-Paley function,we have We take|α|=r,so Fork≤j,takingr=l,where the nnmberlis the smallest integer larger thans,we have Fork>j,takingr=0,we have Now give the proof of(2)of Theorem 2. Similarly,we have Using 2?jt+2?js Noting lemma 1,we finish the proof. Theorem 3Let σ is a bilinear symbol in the forbidden classthenTσcan be extended as a bounded operator ProofLet us turn to the proof of Part(1).Letwe will show thatTσk(f,g)∈fork=1,2,3.Lets1≤s2,ands=min(s1,s2)?ε=s1?ε.We have So and So ForTσ2,we proceed analogously,obtaining the better estimate Using embedded relations aboutwe obtain the required boundedness ofT. The estimate for the part(2)of Theorem 3 is obtained essentially the same way as in part(1)of Theorem 3.Hence the proof of Theorem 3 is completed.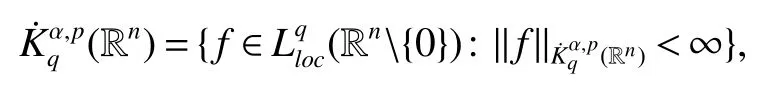
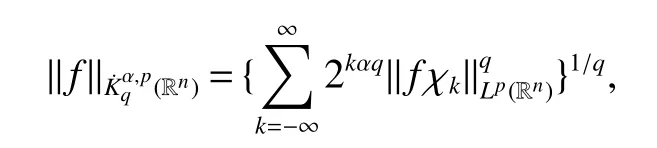
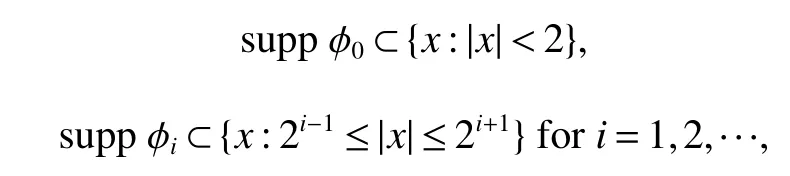
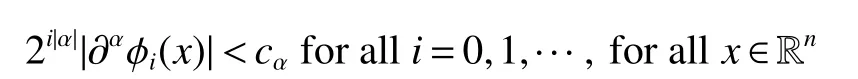
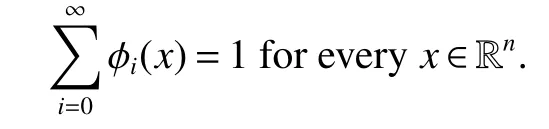
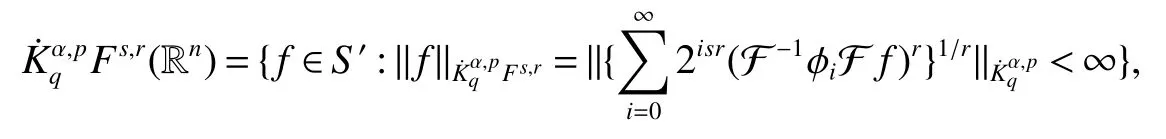
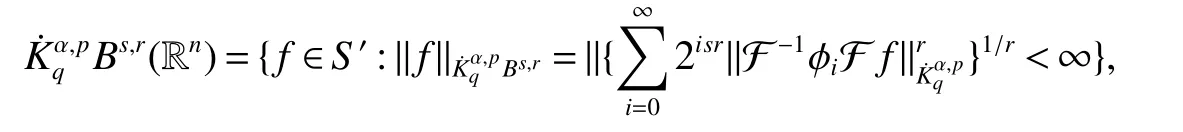
3 Main theorems and proofs