The Role of a1(1260)in π?p →(1260)p and π?p → π?ρ0p Reactions Near Threshold?
Chen Cheng(程晨),Ju-Jun Xie(謝聚軍),,3,? and Xu Cao(曹須),3
1Institute of Modern Physics,Chinese Academy of Sciences,Lanzhou 730000,China
2University of Chinese Academy of Sciences,Beijing 100049,China
3Research Center for Hadron and CSR Physics,Institute of Modern Physics of CAS and Lanzhou University,Lanzhou 730000,China
1 Introduction
Within the picture of classical quark model,the mesons are bound states of quarks and antiquarks.This picture is very successful.Most of the known mesons can be described very well within the quark model.[1]However,it seems that the meson spectrum is much richer than that predicted by the quark model.There is a growing set of experimental observations of resonance-like structures with quantum numbers,which are forbidden for the quark-antiquark system or situated at masses,which cannot be explained by the quark-antiquark model.[2?3]For example,the new observations[4?10]have challenged the conventional wisdom that mesons are made of quarkantiquark pairs in the low energy region.
In the quark model,the a1(1260)and b1(1235)are ground states of axial-vector resonances with quantum numbers IG(JPC)= 1?(1++)and 1+(1+?),respectively.For a1(1260)resonance,the experimental mass ma1(1260)=(1230±40)MeV is more precisely than its width Γa1(1260)=(250–600)MeV assigned by the Particle Data Group.[1]A recent COMPASS measurement published in 2010[11]provides a much smaller uncertainty of the width Γa1(1260)=367±MeV and mass ma1(1260)=1255±MeV.
In the chiral unitary approach,the a1(1260)and b1(1235)are composite particles of a vector meson and a pseudoscalar meson in coupled channels.[12?13]Indeed,the a1(1260)is dynamically generated from the K?ˉK and ρπ channels and the couplings of the a1(1260)to these channels can be also obtained at the same time.[13]Based on these results,the radiative decay of a1(1260)meson was studied in Refs.[14–15],where the theoretical calculations agree with the experimental values within uncertainties.On the other hand,the effects of the next-to-leading order chiral potential on the dynamically generated axial-vector mesons were studied in Ref.[16].It was found that the inclusion of the higher-order kernel does not change the results obtained with the leading-order kernel in any significant way,which gives more supports to the dynamical picture of the a1(1260)state.[12?13,16]
Recently the COMPASS collaboration[9]reported the observation of a resonance-like structure around 1.42 GeV with axial-vector quantum numbers 1?(1++)in the f0(980)π P-wave of the π?π?π+final state,and it was claimed as a signal as a new resonance that was named the“a1(1420)”state with width around 140 MeV.It is very difficult to explain this structure as a new state within the quark model,because the radial excitation of a1(1260)is expected to have a mass above 1650 MeV.Furthermore,it is not expected that the radial excitation state has a width,which is much smaller than the one of the ground state.In Refs.[17–18],the “a1(1420)” state can be explained as a triangle singularity via the decay of a1(1260)into K?ˉK and subsequent re-scattering of the K from the K?decay to form the f0(980)resonance.In Ref.[19],the production of a1states are studied in heavy meson decays,which can also provide insights to the a1(1420)and the future experimental analyses will very probably lead to a deeper understanding of the nature of the a1(1420).
In this work,we study the role of a1(1260)resonance in the π?p →(1260)p and π?p → ρ0π?p reactions near threshold using an effective Lagrangian approach.Unfortunately,as discussed before,the uncertainty of total decay width of a1(1260)is large and the branch ratio of a1(1260)→ ρπ is unknown,we can not obtain directly the coupling of a1(1260)to the ρπ channel from the partial decay width of a1(1260)resonance.Thus,it is necessary to rely on theoretical schemes.In this calculation,we take the coupling of a1(1260)to the ρπ channel that was obtained in Ref.[13]with the picture that the a1(1260)resonance is dynamically generated from the K?ˉK and ρπ coupled channels.In this respect,our calculations are based on the dynamical picture of the a1(1260)state.We consider the t channel ρ0exchange.The total cross sections of π?p →(1260)p reaction are calculated.It is found that the theoretical calculations for the total cross sections of π?p →(1260)p reaction are in agreement with the experimental data.In addition,the total and differential cross sections for the π?p →(1260)p → ρ0π?p reaction are predicted and could be tested by future experiments.Because the main decay channel of a1(1260)resonance is the ρπ channel,the π?p →(1260)p → ρ0π?p reaction is very useful to deep understanding the nature of a1(1260)state and also the nature of the a1(1420).
This paper is organized as follows.In Sec.2,formalism and ingredients used in the calculation are given.In Sec.3,the results are presented and discussed.Finally,a short summary is given in the last section.
2 Formalism and Ingredients
The combination of effective Lagrangian method and isobar model is an important theoretical approach in describing the meson production processes. In this section,we introduce the theoretical formalism and ingredients for studying the a1(1260)hadronic production in π?p →(1260)p and π?p → ρ0π?p reactions within the effective Lagrangian method and isobar model.
2.1 Feynman Diagrams and Interaction Lagrangian Densities
The basic tree level Feynman diagrams for the π?p →(1260)p and π?p → ρ0π?p reactions are depicted in Figs.1 and 2,respectively.For these reactions,the tchannel ρ0exchange is considered in this calculation,since the main decay channel of a1(1260)is the ρπ channel.
To compute the contributions of diagrams shown in Figs.1 and 2,we use the interaction Lagrangian density for the ρNN vertex as in Refs.[20–23],

where the parameters are taken as commonly used ones:[24?28]gρNN=3.36 and κρ=6.1.
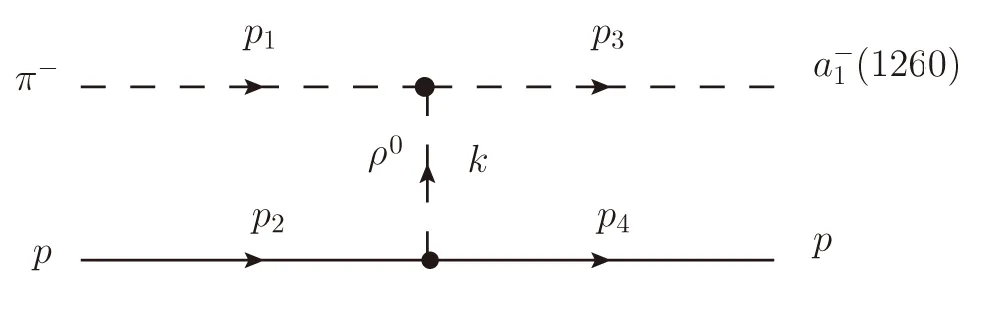
Fig.1 Feynman diagram for π?p → (1260)p reaction.We show also the definition of the kinematical(p1,p2,p3,p4,and k)that we use in the present calculation.In addition,we use k=p2?p4.

Fig.2 Feynman diagram for π?p → ρ0π?p reaction.
In addition,we need also the effective interaction of the a1(1260)ρπ vertex.As mentioned before,in the chiral unitary approach of Ref.[13],the a1(1260)resonance is dynamically generated from the interaction ofand ρπ interactions.One can write down the(1260)vertex as,
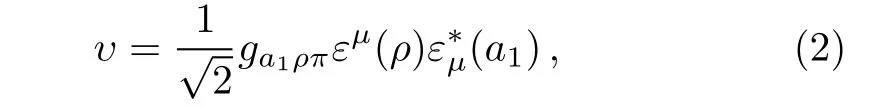
where εμ(ρ)and(a1)are the polarization vectors of ρ and a1(1260).The ga1ρπis the coupling constant of the a1(1260)to the ρπ channel,which is taken to be(?3795,2330)MeV as obtained in Ref.[13].The factorin Eq.(2)accounts for the fact that in the I=1 and I3= ?1 combination of ρπ mesons,

2.2 Scattering Amplitudes and Cross Sections
With the effective Lagrangian densities given above,we can straightforwardly construct the invariant scattering amplitude for π?p →(1260)p reaction corresponding to the Feynman diagram in Fig.1:

where s4,s2,and s3are the polarization variables of final proton,initial proton and a1(1260)resonance,respectively.The ρ-meson propagator Gμν(k)is,

where mρis the mass of the ρ meson and we take mρ=775.26 MeV.
In Eq.(4),Fρ(k)is the form factor for ρNN vertex and we take it as in Refs.[20–21],

with Λρthe cut o ffparameter,which will be discussed in the following.
Similarly,we can get the invariant scattering amplitude for π?p → π?ρ0p reaction corresponding to the Feynman diagram in Fig.2:
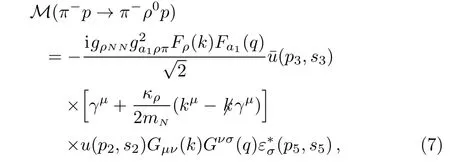
where s5is the polarization variable of ρ0meson,and Gνσ(q)is the a1(1260)propagator,

where Γa1and ma1are the width and mass of the a1(1260)resonance,respectively.We take ma1=1230 MeV.For Γa1,as mentioned above,since its value has large uncertainties,we take Γa1=(250,425,and 600)MeV for comparison.
In Eq.(7),Fa1(q)is the form factor of a1(1260)state.In our present calculation,we adopt the following form as in many previous works:[24?28]

where Λa1is the cuto ffparameter of a1(1260)resonance.
The differential cross section in the center of mass frame(c.m.)for the π?p →(1260)p and π?p → ρ0π?p reactions can be derived from the invariant scattering amplitude square|M|2,reading as:

where W is the invariant mass of the π?p system,whereas,θ denotes the scattering angle of the outgoing(1260)resonance relative to π?beam direction in the c.m.frame.In the above equation,andare the 3-momenta of the initial π?meson and the final a1(1260)mesons,

where λ(x,y,z)is the K?hlen or triangle function.We take mp=938.27 MeV and mπ?=139.57 MeV in this calculation.
In the effective Lagrangian approach,the sum over polarizations and the Dirac spinors can be easily done thanks to

With the formalism and ingredients given above,the calculations of the differential and total cross sections for π?p→ ρ0π?pare straightforward:

3 Numerical Results and Discussion
With the formalism and ingredients given above,the total cross section versus the beam momentum(plab)??The relation between W(or s for the case of π?p → π?ρ0p reaction)and plabis:s=of the π?meson for the π?p →(1260)p reaction is evaluated.The numerical results are shown in Fig.3 for beam energies plabfrom just above the production threshold 2.0 GeV to 5.0 GeV together with the experimental data[29?30]for comparison.In Fig.3,the dashed,solid,and dotted curves represent the theoretical results obtained with Λρ=(1.4,1.5,and 1.6)GeV,respectively.One can see that the experimental data can be reproduced with a reasonable value of the cuto ffparameter Λρ=1.5±0.1 GeV.The experimental data from Ref.[29]were measured at plab=3.2 GeV and 4.2 GeV,which can be well reproduced with Λρ=1.5 GeV.However the experimental data from Ref.[30]at plab=3.89 GeV is a few hundredμb larger than the expected value.More experimental measurements are needed to complement the limited data in Refs.[29–30],and give valuable information about the mechanism of this reaction.
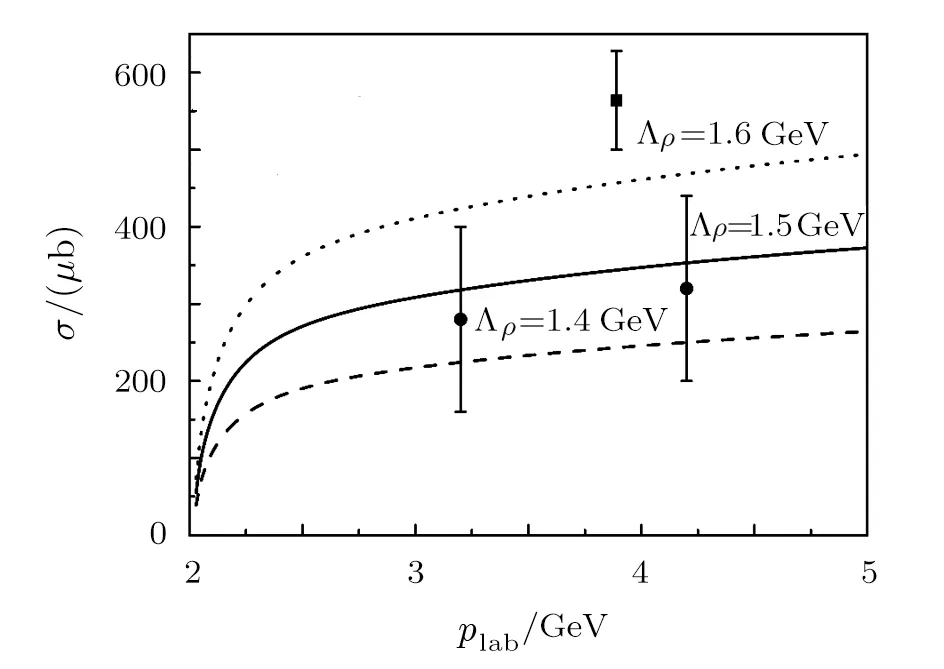
Fig.3 Total cross section of π?p → a?1(1260)p reaction versus the incoming π? beam momentum in the laboratory frame.The circle data points represent the experimental data from Ref.[29],while the square point represents the experimental data from Ref.[30].
Based on the results of the process of π?p →(1260)p,we investigate the reaction of π?p →(1260)p → ρ0π?p.The theoretical calculations of the total cross sections of this reaction are shown in Fig.4,where we take Λa1= Λρ=1.5 GeV for simplicity.It is worth to mention that the numerical results are not sensitive to the value of Λa1.In Fig.4,the dashed,solid,and dotted curves are obtained with Γa1=(250,425,and 600)MeV,respectively.

In addition to the total cross sections of π?p →(1260)p → ρ0π?p reaction,we calculate also the differential cross section for this reaction as a function of Mρπat plab=4 GeV.The theoretical results are shown in Fig.5,where the dashed,solid,and dotted curves are obtained with Γa1=(250,425,and 600)MeV,respectively.The numerical results shown in Figs.4 and 5 could be tested by the future experiments.

Fig.5 Invariant mass distributions dσ/dMρπ of π?p →(1260)p → ρ0π?p reaction at plab=4 GeV.
It is worth to mention that though the effective Lagrangian approach is a convenient tool to catch the qualitative features of the π?p →and π?p →(1260)p → π?ρ0p reactions,it is not consistent with the unitary requirements,which in principle are important for extracting the parameters of the excited states from the analysis of the experimental data,[31?33]especially for those reactions involving many intermediate couple channels and three-particle final states.[34?35]In this work,basing on phenomenological Lagrangians,we consider only the tree-diagram contributions,in which the unitarity condition is not ensured and coupled channel effects are not taken into account.However,our model can give a reasonable description of the experimental data in the considered energy region for the reaction of π?p →(1260)p reaction.Meanwhile,our calculation o ff ers some important clues for the mechanisms of the π?p →(1260)p and π?p →(1260)p → π?ρ0p reactions and makes a first effort to study the role of a1(1260)resonance in these relevant reactions.Furthermore,including such unitarity condition and the coupled channel effects,the scattering amplitudes would become more complex due to additional parameters,and we can not determine or constrain these parameters.Hence,we will leave these contributions to future studies when more experimental data become available.
4 Summary
In this work,we have investigated the π?p →(1260)p and π?p → a?1(1260)p → π?ρ0p reactions near threshold within an effective Lagrangian approach.The t-channel ρ0meson exchange process is considered with the assumption that the a1(1260)resonance was dynamically generated from the coupledand ρπ channels,from where we can get the coupling of a1(1260)to ρπ channel.The total cross section of π?p →(1260)p is calculated with the coupling constant of the a1(1260)to ρπ channel obtained from the chiral unitary theory and a reasonable value of cut o ffparameter Λρ.It is found that the experimental measurement for the π?p → a?1(1260)p reaction can be fairly reproduced.
Furthermore,the total and differential cross sections of π?p →(1260)p → π?ρ0p reaction are also predicted based on the results of the study of the π?p →(1260)p.Because the width of a1(1260)resonance has large uncertainty,we take different values of Γa1for comparison.It is expected that our model calculations can be tested by future experiments.
Finally,we would like to stress that,thanks to the important role played by the t-channel ρ0exchange in the π?p →(1260)p reaction,one can reproduce the available experimental data with a reasonable value of the cut o ffparameter in the form factors.The π?p →(1260)p and π?p →(1260)p → π?ρ0p reactions are important for the study of the a1(1260)resonance.More and accurate data for these reactions will provide valuable information on the reaction mechanisms and can be used to test our model calculations,which should be tied to the nature of the a1(1260)state.This work provides a vision in this direction.
One of us(C.C.)would like to thank Yin Huang for helpful discussions.We thank Satoshi Nakamura for useful discussions.
[1]K.A.Olive,et al.,[Particle Data Group Collaboration],Chin.Phys.C 38(2014)090001;doi:10.1088/1674-1137/38/9/090001.
[2]E.Klempt and A.Zaitsev,Phys.Rept.454(2007)1;doi:10.1016/j.physrep.2007.07.006;[arXiv:0708.4016[hepph]].
[3]N.Brambilla,et al.,Eur.Phys.J.C 74(2014)2981;doi:10.1140/epjc/s10052-014-2981-5[arXiv:1404.3723[hep-ph]].
[4]S.K.Choi et al.,[Belle Collaboration],Phys.Rev.Lett.91(2003)262001;[hep-ex/0309032].
[5]D.Acosta,et al.,[CDF Collaboration],Phys.Rev.Lett.93(2004)072001;[hep-ex/0312021].
[6]V.M.Abazov,et al.,[D0 Collaboration],Phys.Rev.Lett.93(2004)162002;[hep-ex/0405004].
[7]M.Ablikim,et al.,[BESIII Collaboration],Phys.Rev.Lett.110(2013)252001;[arXiv:1303.5949[hep-ex]].
[8]Z.Q.Liu,et al.,[Belle Collaboration],Phys.Rev.Lett.110(2013)252002;[arXiv:1304.0121[hep-ex]].
[9]C.Adolph,et al.[COMPASS Collaboration],Phys.Rev.Lett.115 (2015) 082001; doi:10.1103/Phys RevLett.115.082001[arXiv:1501.05732[hep-ex]].
[10]V.M.Abazov et al.,[D0 Collaboration],Phys.Rev.Lett. 117 (2016) 022003; doi:10.1103/PhysRev Lett.117.022003[arXiv:1602.07588[hep-ex]].
[11]M.Alekseev et al.,[COMPASS Collaboration],Phys.Rev.Lett.104(2010)241803;doi:10.1103/PhysRev Lett.104.241803[arXiv:0910.5842[hep-ex]].
[12]M.F.M.Lutz and E.E.Kolomeitsev,Nucl.Phys.A 730(2004) 392; doi:10.1016/j.nuclphysa.2003.11.009[nuclth/030 7039].
[13]L.Roca,E.Oset,and J.Singh,Phys.Rev.D 72(2005)014002; doi:10.1103/PhysRevD.72.014002[hepph/05 03273].
[14]L.Roca,A.Hosaka,and E.Oset,Phys.Lett.B 658(2007)17;doi:10.1016/j.physletb.2007.10.035[hepph/0611075].
[15]H.Nagahiro,L.Roca,A.Hosaka,and E.Oset,Phys.Rev.D 79 (2009)014015;doi:10.1103/Phys RevD.79.014015[arXiv:0809.0943[hep-ph]].
[16]Y.Zhou,X.L.Ren,H.X.Chen,andL.S.Geng,Phys.Rev.D 90(2014)014020;doi:10.1103/PhysRev D.90.014020[arXiv:1404.6847[nucl-th]].
[17]M.Mikhasenko, B. Ketzer, and A.Sarantsev,Phys.Rev.D 91 (2015)094015;doi:10.1103/Phys RevD.91.094015[arXiv:1501.07023[hep-ph]].
[18]F.Aceti,L.R.Dai,and E.Oset,arXiv:1606.06893[hepph].
[19]W.Wang and Z.X.Zhao,Eur.Phys.J.C 76(2016)59; doi:10.1140/epjc/s10052-016-3900-8[arXiv:1511.06998[hep-ph]].
[20]R.Machleidt,K.Holinde,and C.Elster,Phys.Rept.149(1987)1;doi:10.1016/S0370-1573(87)80002-9.
[21]R.Machleidt,Adv.Nucl.Phys.19(1989)189.
[22]M.Doring,C.Hanhart,F.Huang,S.Krewald,U.G.Meissner,and D.Ronchen,Nucl.Phys.A 851(2011) 58; doi:10.1016/j.nuclphysa.2010.12.010[arXiv:1009.3781[nucl-th]].
[24]K.Tsushima,A.Sibirtsev,and A.W.Thomas,Phys.Rev.C 62(2000)064904;doi:10.1103/PhysRevC.62.064904[nucl-th/0004011].
[25]A.M.Gasparyan,J.Haidenbauer,C.Hanhart,and J.Speth,Phys.Rev.C 68(2003)045207;doi:10.1103/Phys RevC.68.045207[nucl-th/0307072].
[26]J.J.Xie and B.S.Zou,Phys.Lett.B 649(2007)405;doi:10.1016/j.physletb.2007.04.035[nucl-th/0701021].
[27]J.J.Xie,B.S.Zou,and H.C.Chiang,Phys.Rev.C 77 (2008) 015206; doi:10.1103/PhysRevC.77.015206[arXiv:0705.3950[nucl-th]].
[29]S.U.Chung,O.I.Dahl,J.Kirz,and D.H.Miller,Phys.Rev.165(1968)1491;doi:10.1103/PhysRev.165.1491.
[30]P.G.Wohlmut,K.Abe,A.D.Johnson,and V.J.Stenger,Nucl.Phys.B 18(1970)505;doi:10.1016/0550-3213(70)90132-X.
[31]H.Kamano,B.Julia-Diaz,T.S.H.Lee,A.Matsuyama,and T.Sato,Phys.Rev.C 80(2009)065203;doi:10.1103/PhysRevC.80.065203[arXiv:0909.1129[nuclth]].
[32]N.Suzuki,B.Julia-Diaz,H.Kamano,T.S.H.Lee,A.Matsuyama,and T.Sato,Phys.Rev.Lett.104(2010)042302;doi:10.1103/PhysRevLett.104.042302[arXiv:0909.1356[nucl-th]].
[33]S.X.Nakamura,H.Kamano,T.S.H.Lee,and T.Sato,Phys.Rev.D 86 (2012)114012;doi:10.1103/Phys RevD.86.114012[arXiv:1209.3402[hep-ph]].
[34]H.Kamano,B.Julia-Diaz,T.S.H.Lee,A.Matsuyama,and T.Sato,Phys.Rev.C 79(2009)025206;doi:10.1103/PhysRevC.79.025206[arXiv:0807.2273[nuclth]].
[35]H.Kamano,S.X.Nakamura,T.S.H.Lee,and T.Sato,Phys.Rev.D 84 (2011)114019;doi:10.1103/Phys RevD.84.114019[arXiv:1106.4523[hep-ph]].
 Communications in Theoretical Physics2016年12期
Communications in Theoretical Physics2016年12期
- Communications in Theoretical Physics的其它文章
- Pressure Oscillating Flow in Corrugated Parallel Channel?
- Strong Decays of Charm Mesons (2680),(2760),(3000)?
- Dilepton from Passage of Jets Through Spherical Expanding QGP?
- Free Convective Nonaligned Non-Newtonian Flow with Non-linear Thermal Radiation
- Weibel Instability Growth Rate in Magnetized Plasmas with Quasi-Relativistic Distribution Function
- Quantum Private Comparison of Equality Based on Five-Particle Cluster State?
