Dilepton from Passage of Jets Through Spherical Expanding QGP?
Yong-Ping Fu(傅永平)and Qin Xi(郗勤)
School of Physics and Mathematics,Dianxi Science and Technology Normal University,Lincang 677000,China
1 Introduction
Relativistic heavy-ion collisions are studied with the aim of producing a strongly interacting matter,the deconfined matter is the so-called quark-gluon plasma(QGP).The photons and dileptons production is considered to be a useful probe for the evolution of the QGP due to their very long mean free path in the hot matter.[1]In relativistic heavy-ion collisions dileptons are produced from the Drell–Yan process,[2]the interactions of thermal partons in the QGP,[3]jets passing through the hot medium(jet-dilepton conversion),[4?5]the hadron interactions in the hadronic gas,[6?7]and the hadronic decays after the freeze-out.[8]
The jet-dilepton conversion when the jets passing through the QGP also provides a useful tool that enables tomographic study of the QGP.[9?10]The electromagnetic radiation from jets interacting with the thermal partons of the QGP in the(1+1)-dimensional((1+1)D)evolution of the plasma has been investigated.[11?13]The solutions of the relativistic hydrodynamical equations can provide the collective properties of the flow.The Bjorken solution describes an estimate of the(1+1)D cylindrical expansion of the QGP.[14]
The(1+3)-dimensional((1+3)D)hydrodynamics equations have been studied numerically which assumes cylindrical symmetry along the transverse direction and boost invariant along the longitudinal direction.[15?18]When the initial proper time τ= τiand initial temperature T=Tithe system is thermalized.The QGP temperature T and proper time τ can be numerically calculated.The transverse flow effect of the dilepton production with cylindrical symmetry are shown to be important in the region of low invariant mass.[17]
In the present work,we derive the hubble-like solutions(τT= τiTi)of(1+3)D relativistic hydrodynamics which favors spherical symmetry,and investigate the initial condition of the temperature T and proper time τ in the spherical evolution.We find the transverse flow effect is also apparent at intermediate and high invariant mass at LHC energies.
Jets passing through the plasma will lose energies.In the high energy parton collisions,the radiative energy loss is more important than the elastic energy loss.[19]The AMY model is used to investigate the energy loss of the jet-dilepton conversion in the(1+1)D QGP.[4?5,11?12]There are several models of the jet energy loss due to gluon bremsstrahlung in the QGP:Gyulassy–Wang(GW),[19?20]Gyulassy–Levai–Vitev(GLV),[21?22]Baier–Dokshitzer–Mueller–Peigne–Schi ff(BDMPS),[23?24]Guo-Wang(HT),[25?26]Wang–Huang–Sarcevic(WHS),[27?28]and Arnold–Moore–Ya ff e(AMY).[29?30]In this paper we use the WHS and BDMPS models to calculate the energy loss of the jet-dilepton conversion with the(1+3)D spherical symmetry.
This paper is organized as follows.In Sec.2 we discuss the(1+3)D spherical evolution of the plasma.In Sec.3 we calculate the jet production and jet energy loss.In Sec.4 we discuss the production rate of the jet-dilepton conversion in the spherical expanding QGP.Finally,the numerical results and summary are presented in Secs.5 and 6.
2(1+3)Dimension Hydrodynamics
The energy-momentum tensor of the QGP produced in relativistic heavy-ion collisions is given by Tμν=(ε+P)uμuν? Pgμν,where ε and P are the energy density and the pressure,respectively.The four-velocity of the ideal fluid is uμ= γ(1,v),where γ =1/(1? v2)1/2.The space-time coordinate is xμ=(t,r),and the metric tensor is gμν=diag(1,?1,?1,?1).The tensor satisfies(gμν)2=1+d, δii=d,where Greek letters denote Lorentz indices,Latin letters denote three-vector indices,and d is the dimensionality of the space.In(1+3)D ideal fluid,the fluid velocity vector uμ= xμ/τ is Lorentz invariant,the proper time is τ=(t2? r2)1/2,where we denote|r|by r and the space-time rapidity η as η=1/2ln((t+r)/(t?r)),the t and r coordinates as functions of τ and η are t= τ coshη,and r= τ sinhη.Under the condition of spherical expansion of the fire ball,we have the space-time integration as

where the Jacobian dtdr is related to τdτ dη.
Now the relativistic hydrodynamic equation ?μTμν=0 for a(1+3)D expansion with spherical symmetry read
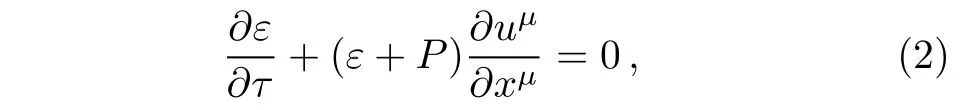
where?uμ/?xμ=(?1)/τ.If the QGP has the longitudinal and transverse expansion,we derive the universal solution of the relativistic hydrodynamics equation as
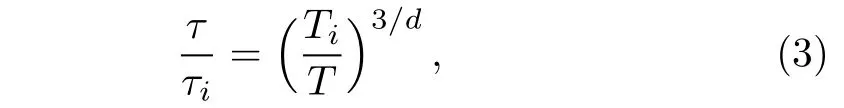
where τiand Tiare the initial time and initial temperature of the equilibrium QGP,respectively.In the(1+1)D case,d=1,Eq.(3)is the well-known Bjorken solution.
In the(1+3)D condition,d=3,we have the Hubblelike solution as

this solution favors the spherical symmetry.[32]The end of the QGP phase occur at proper time τc= τiTi/Tc,where Tc=160 MeV is the critical temperature of the phase transition.In the(1+1)D cylindrical expansion the QGP cooling time is τc= τi(Ti/Tc)3.The transverse expansion leads to a more rapid cooling of the system.
At proper time τiand temperature Tithe initial entropy Siis essentially constant and the system is regarded as thermalized.[17]Since the initial entropy density is related to the initial temperature as[16]
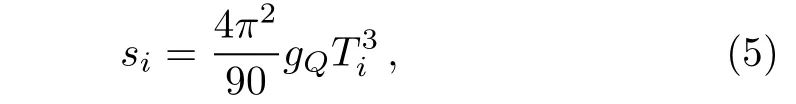
where the factor gQ=42.25 is the degrees of freedom for the plasma of u,d,s quarks and gluons.Therefore the total entropy is

the space volume is dV =r2τ dη sinθdθd?.Then we have that the initial entropy per unit rapidity is

The entropy density and particle multiplicity for the case of spherical expansion have the relation as[15?16]

where y is the true momentum rapidity.In the(1+3)D expanding QGP,the space-time rapidity η=(1/2)[(t+r)/(t?r)]and the true momentum rapidity y=(1/2)[(E+p)/(E?p)]are correlated.[17]Then we have dy=dη and η=y+,whereis an arbitrary constant.At midrapidity y=0,η=,we define r(η,y=0)=τ.Therefore the initial time and temperature for the(1+3)D spherical expansion are related by the following
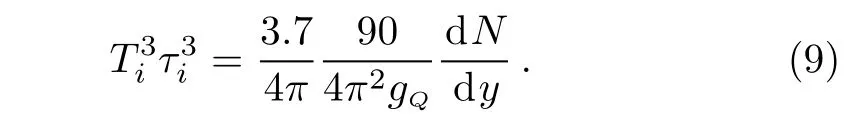
We use the initial temperature Ti= 370 MeV for dN/dy=1260 at RHIC,Ti=636 MeV for dN/dy=2400 at LHC (Pb+Pb,= 2.76 TeV),and Ti=845 MeV for dN/dy=5624 at LHC(Pb+Pb,=5.5 TeV).[11?12,33?34]The numerical results of the initial conditions for y=0 are presented in Table 1.

Table 1 Initial conditions of the hydrodynamical expansion.
3 Jet Energy Loss
The energy loss of jets passing the QGP can be determined by the spectrum of energy loss per unit distance dE/dx.Induced gluon bremsstrahlung is more important than the elastic scattering of partons in the jet energy loss.[23]If an energetic jet hadronizes outside the system,the passing distance is long and the energy loss is large.[19,23,27?28]However,in the jet-dilepton and jet-photon conversion,jets travel only a short distance through the QGP before the jets convert into dileptons and photons.Therefore the energy loss is relatively small in the jet-dilepton and jet-photon conversions.In the central Au+Au collisions at RHIC the energy loss of the jetphoton conversion is just about 20%.[5]
In this paper we discuss the jets produced at midrapidity and propagated in the transverse direction.The total passing distance of a hadronization jet produced at(r,?)in(1+3)D is? rcos?,where R(τ)is the radius of the expanding QGP.In the(1+1)D Bjorken evolution,the average value ofwhere RA=1.2A1/3fm is the initial radius of the system.[11,28]We consider the spherical expansion,and find that R(τ) ≥ RAand
In the relativistic heavy-ion collisions,we assume the high energy jet is massless and travels with the speed of light in the transverse direction.[11]The distance of the jets passing through the QGP in the jet-dilepton conversion processes is
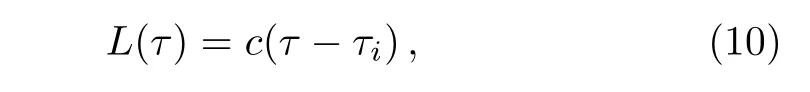
and the average value of the distance of jet-dilepton processes is

where the lifetime of the QGP phase is△τ= τc?τi.In Table 2 we plot the numerical results of the jet-dilepton distance and hadronization distance,we find that the distance hLi of the jet-dilepton conversion is smaller than the total distance h?Li of hadronization.In the jet-dilepton conversion processes the high energy jets only pass a short distance in the hot matter before the jets convert into dileptons.The distance hLi1+3is smaller than hLi1+1at RHIC and LHC energies due to the transverse flow effect.

Table 2 The average value of the distance covered by the jet during the passage of the jet-dilepton conversion and total distance in(1+1)D and(1+3)D expanding QGP,respectively.
In Refs.[9,27–28]the authors use the WHS model to calculate the modification of the jet fragmentation function due to the energy loss.This model is a good tool to study the parton energy loss and multiple final-state scatterings.[28]The yield dNjet/d2p⊥dyjetfor a jet passing through the QGP can be written as
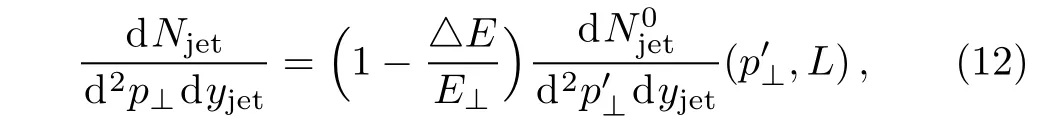
where△E=nεais the energy loss,E⊥is the transverse energy of the produced jet,εais the average energy loss per scattering.p′⊥is the transverse momentum of the parton,and p⊥=p′⊥?△E.The energy-loss in the medium of a finite size L is given by BDMPS:[23]

where ca=4/3 for quarks and 3 for gluon,μ2=4παsT2,μ is the Debye mass of the medium,λgis the gluon mean free path.The quark mean free path is λq=9λg/4.[27?28]
The initial jets production dN0jet/d2p′⊥dyjetin the relativistic heavy-ion collisions(A+B→jets+X)can be written as[35]
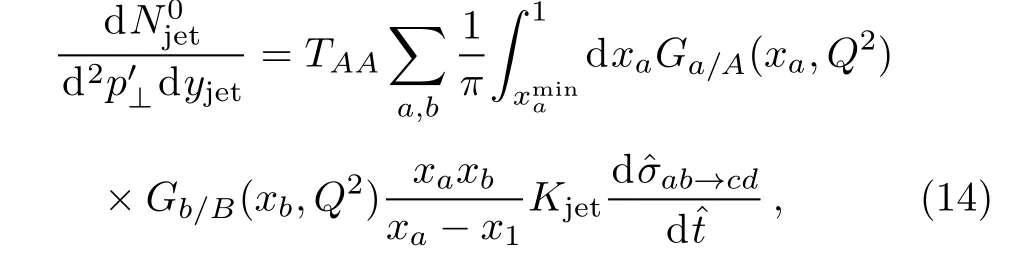
where TAA=9A2/8πis the nuclear thickness for central collisions.[4?5]The momentum fractions with the rapidity are given by=x1/(1?x2)and xb=xax2/(xa?x1),where the variables areis the center of mass energy of the colliding nucleons.Kjetis the pQCD correction factor to take into account the next-to-leading order(NLO)effects,we use Kjet=1.7 for RHIC and 1.6 for LHC.[30]The parton distribution for the nucleus is given by

where Z is the number of protons,A is the number of nucleons,(xa,Q2)is the nuclear modification function.[36]The functions fa/p(xa,Q2)and fa/n(xa,Q2)are the parton distributions of the proton and neutron,respectively.[37]is the cross section of parton collisions at leading order,these processes are:qˉq→q′ˉq′,qq′→qq′,qˉq′→qˉq′,qq→qq,qˉq→qˉq,qg→qg,and gg→qˉq.[38]
4 Jet-Dilepton Conversion
The production rate of the jet-dilepton conversion is given by[13]
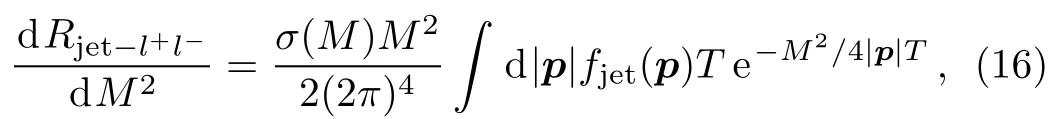
where the cross section of the quark annihilation is σ(M)=1PThe jet-dilepton conversion is sensitive to the choice of the minimum value of p.We use the limit|p|≥ 4 GeV in Eq.(16).[11?12]The phasespace distribution function for a jet,assuming the constant transverse density of nucleus,is as follows[39]where gq=6 is the spin and color degeneracy of the quarks(and antiquarks),V=4πτ3is the volume of the spherical expanding QGP.

The production rate of thermal dileptons from the QGP can be written as[3,40]

Because we are interested in jets produced at midrapidity(yjet=0),we only consider dileptons produced at midrapidity(y=0).The yield as a function of invariant mass M and dilepton rapidity y is given by the(1+3)D space-time integration d4x=r2τ dτdy sinθdθd? as

In the jet-dilepton conversion processes the jet only propagates in the pure QGP phase,therefore we limit the τ integration as[τi,τc].
5 Results and Discussions
The numerical results of thermal dileptons produced from the QGP at RHIC and LHC energies are presented in Fig.1.In the central Au+Au collisions at200 GeV we choose the initial temperature of the(1+3)D spherical expanding QGP Ti=370 MeV.[11?12]Then we have the initial time

and the critical time τc= τiTi/Tc=3.33 fm/c.In the(1+1)D Bjorken expansion the initial time[15]

is 0.26 fm/c and the critical time τc=τi(Ti/Tc)3is 3.22 fm/c at RHIC.The life time of the QGP phase of the(1+3)D expansion(△τ1+3=1.89 fm/c)is smaller than the one of the(1+1)D case(△τ1+1=2.96 fm/c)at RHIC energy.At LHC we have △τ1+3=3.092 fm/c,△τ1+1=5.442 fm/c,and △τ1+3=4.453 fm/c,△τ1+1=12.873 fm/c corresponding to Ti=636 MeV and Ti=845 MeV,respectively.The initial conditions at RHIC and LHC are calculated in Table 1.
The comparisons of the thermal dileptons and the jetdilepton conversion from the(1+1)D cylindrical expanding and(1+3)D spherical expanding QGP are given in Figs.1 and 2,respectively.The transverse flow of the spherical expansion reduces the yields from low to high invariant mass and the reduction is largest at low invariant mass,the transverse flow effect is still important at intermediate and large mass. In Fig.1 the reduction of thermal dileptons is in the region of M<2.5 GeV for Ti=370 MeV,M<4.5 GeV for Ti=636 MeV and M<6 GeV for Ti=845 MeV.The thermal production is suppressed by a factor~2 at M~2 GeV for Ti=845 MeV.In Fig.2 the reduction of the jetdilepton conversion is in the region of M<7 GeV for Ti=370 MeV,M<13.5 GeV for Ti=636 MeV and M<16 GeV for Ti=845 MeV.We find a factor~2 of suppression at M~4 GeV for Ti=845 MeV.
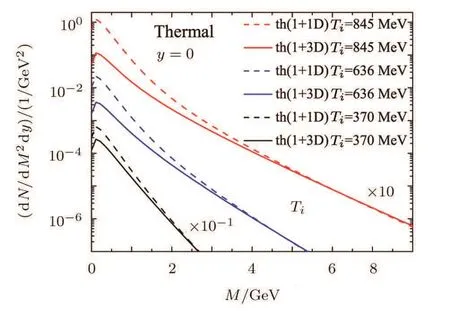
Fig.1 The results of thermal dileptons produced from the QGP phase at RHIC and LHC energies.In central Au+Au collisions at=200 GeV the initial temperature is Ti=370 MeV.In central Pb+Pb collisions at=2.76 TeV and 5.5 TeV,the initial temperature is Ti=636 MeV and Ti=845 MeV,respectively.The dashed line means the thermal dileptoons produced from the cylindrical expanding QGP without transverse flow(1+1D).The solid line means thermal dileptons produced from spherical expanding QGP(1+3D).

Fig.2 Dileptons originating from the passage of the jets passing through the QGP at RHIC and LHC energies.Dashed line:jet-dilepton conversion without transverse flow;solid line:jet-dilepton conversion with transverse flow of the spherical expansion.The jet energy loss is included.
In Figs.3,4,and 5,we plot the numerical results for dileptons from QGP,Drell–Yan process and jet-dilepton conversions in the spherical expanding QGP at RHIC and LHC energies,respectively.In Fig.3 we find the contribution of the jet-dilepton conversion is not important at RHIC.However the jet-dilepton conversion is comparable to that of the thermal contribution and Drell–Yan process at LHC energies.The jet-dilepton conversion becomes a dominant source in the region of 4.5 GeV Fig.3 Dilepton yield for central Au+Au collisions at=200 GeV.Solid line:thermal dileptons produced from the spherical expanding QGP;dashed line:Drell—Yan contribution;dash-dotted line:dileptons produced by the jet-dilepton conversion.The energy loss is considered. Fig.4 Same as Fig.3 but for central Pb+Pb collisions at=2.76 TeV. The energy loss effect of the jet-dilepton conversion is presented in Fig.6 at RHIC and LHC.The energy loss rate△E/Ejet∝ M?2,this implies that the energy loss effect suppresses the jet-dilepton spectrum,and the suppression decreases with increasing invariant mass M.The energy loss rate depends on the propagating distance L of the jet.In Table 2 we find that hLiLHC>hLiRHIC,the large value of L corresponds to the increase of the energy loss rate.The energy loss is much larger at LHC energies.At RHIC dileptons are reduced by about 23%for M=1 GeV,and 10%for M=4 GeV.These results agree with the numerical results from the AMY approach.[12]In central Pb+Pb collisions atTeV the energy loss is about 13%and 7%at M=4.5 GeV and 5.5 GeV,respectively.Atthe energy loss is about 6%at M=7 GeV and 2%at M=9 GeV. The cˉc(bˉb)pairs produced from the initial hard parton collisions can fragment into D(B)andˉD(ˉB)charm(bottom)mesons.The decay of open charm and bottom mesons is the main background of the thermal and D-Y dileptons.In Refs.[41–43]the authors study the energy loss of heavy quarks and the Parton-Hadron-String Dynamics transport model,and find that the production of the dileptons from the the decays of DˉD and BˉB mesons is smaller than the thermal dileptons in the intermediate and high invariant mass region at LHC.This provides a good window to measure the jet-dilepton conversion in the high invariant mass region. Fig.5 Same as Fig.3 but for central Pb+Pb collisions at=5.5 TeV. Fig.6 E ff ect of jet energy loss on the jet-dilepton conversion at RHIC and LHC energies.The solid lines include the jet energy loss,while the dashed lines do not. We have studied the hydrodynamic equations with spherical symmetry,and calculated the large mass dilepton produced from the jet-dilepton conversion,QGP and Drell–Yan at RHIC and LHC.We presented the temperature evolution equation,which favors the spherical symmetry of fire ball.We have found that the transverse flow effect from the spherical expanding QGP leads to a smaller life time of the QGP phase,and suppresses the production of jet-dileptons and thermal dileptons from low to high invariant mass region.We have found that the energy loss is small when the invariant mass is increasing.The new energy loss framework of jet-dilepton conversion has been presented by using the WHS and BDMPS models. We thank Prof.D.K.Srivastava for helpful suggestions about the transverse expansion of the plasma and energy loss of the jets in the jet-dilepton conversions. [1]E.V.Shuryak,Phys.Lett.B 78(1978)150. [2]S.D.Drell and T.M.Yan,Phys.Rev.Lett.25(1970)316. [3]K.Kajantie,J.Kapusta,L.McLerran,and A.Mekjian,Phys.Rev.D 34(1986)2746. [4]R.J.Fries,B.Muller,and D.K.Srivastava,Phys.Rev.Lett.90(2003)132301. [5]R.J.Fries,B.Muller,and D.K.Srivastava,Phys.Rev.C 72(2005)041902. [6]C.Gale and P.Lichard,Phys.Rev.D 49(1994)3338. [7]C.M.Hung and E.V.Shuryak,Phys.Rev.C 56(1997)453. [8]E.L.Bratkovskaya and W.Cassing,Nucl.Phys.A 619(1997)413. [9]E.Wang and X.N.Wang,Phys.Rev.Lett.89(2002)162301. [10]M.Gyulassy,P.Levai,and I.Vitev,Phys.Lett.B 538(2002)282. [11]D.K.Srivastava,C.Gale,and R.J.Fries,Phys.Rev.C 67(2003)034903. [12]S.Turbide,C.Gale,D.K.Srivastava,and R.J.Fries,Phys.Rev.C 74(2006)014903. [13]Y.P.Fu and Y.D.Li,Nucl.Phys.A 865(2011)76;Y.P.Fu and Y.D.Li,Chin.Phys.Lett.27(2010)101202. [14]J.D.Bjorken,Phys.Rev.D 27(1983)140. [15]R.C.Hwa and K.Kajantie,Phys.Rev.D 32(1985)1109. [16]H.V.Gersdor ff,L.McLerran,M.Kataja,and P.V.Ruuskanen,Phys.Rev.D 34(1986)794. [17]K.Kajantie,M.Kataja,L.McLerran,and P.V.Ruuskanen,Phys.Rev.D 34(1986)811. [18]J.Alam,D.K.Srivastava,B.Sinha,and D.N.Basu,Phys.Rev.D 48(1993)1117. [19]X.N.Wang,M.Gyulassy,and M.Plumer,Phys.Rev.D 51(1995)3436. [20]M.Gyulassy and X.N.Wang,Nucl.Phys.B 420(1994)583. [21]M.Gyulassy,P.Levai,and I.Vitev,Phys.Rev.Lett.85(2000)5535. [22]M.Gyulassy,P.Levai,and I.Vitev,Nucl.Phys.B 571(2000)197. [23]R.Baier,Y.L.Dokshitzer,A.H.Mueller,S.Peigne,and D.Schi ff,Nucl.Phys.B 483(1997)291. [24]R.Baier,Y.L.Dokshitzer,A.H.Mueller,S.Peigne,and D.Schi ff,Nucl.Phys.B 484(1997)265. [25]X.F.Guo and X.N.Wang,Phys.Rev.Lett.85(2000)3591. [26]X.N.Wang and X.F.Guo,Nucl.Phys.A 696(2001)788. [27]X.N.Wang,Z.Huang,and I.Sarcevic,Phys.Rev.Lett.77(1996)231. [28]X.N.Wang and Z.Huang,Phys.Rev.C 55(1997)3047. [29]P.Arnold,G.D.Moore,and L.Ya ff e,J.High Energy Phys.11(2001)057. [30]S.Turbide,C.Gale,S.Jeon,and G.D.Moore,Phys.Rev.C 72(2005)14906. [31]G.Y.Qin,J.Ruppert,C.Gale,S.Jeon,and G.D.Moore,Phys.Rev.C 80(2009)54909. [32]M.I.Nagy,Phys.Rev.C 83(2011)054901. [33]J.Kapusta,L.D.Mclerran,and D.K.Srivastava,Phys.Lett.B 283(1992)145. [34]V.Kumar,P.Shukla,and R.Vogt,Phys.Rev.C 86(2012)054907. [35]J.F.Owens,Rev.Mod.Phys.59(1987)465. [36]K.J.Eskola,V.J.Kolhinen,and C.A.Salgado,Eur.Phys.J.C 9(1999)61. [37]D.Stump,J.Huston,J.Pumplin,et al.,J.High Energy Phys.10(2003)725. [38]B.L.Combridge,J.Kripfganz,and J.Ranft,Phys.Lett.B 70(1977)234. [39]Z.Lin and M.Gyulassy,Phys.Rev.C 51(1995)2177. [40]R.Rapp and E.Shuryak,Phys.Lett.B 473(2000)13. [41]G.D.Moore and D.Teaney,Phys.Rev.C 71(2005)064904. [42]Z.Lin,R.Vogt,and X.N.Wang,Phys.Rev.C 57(1998)899. [43]O.Linnyk,W.Cassing,J.Manninen,E.L.Bratkovskaya,P.B.Gossiaux,J.Aichelin,T.Song,and C.M.Ko,Phys.Rev.C 87(2013)014905.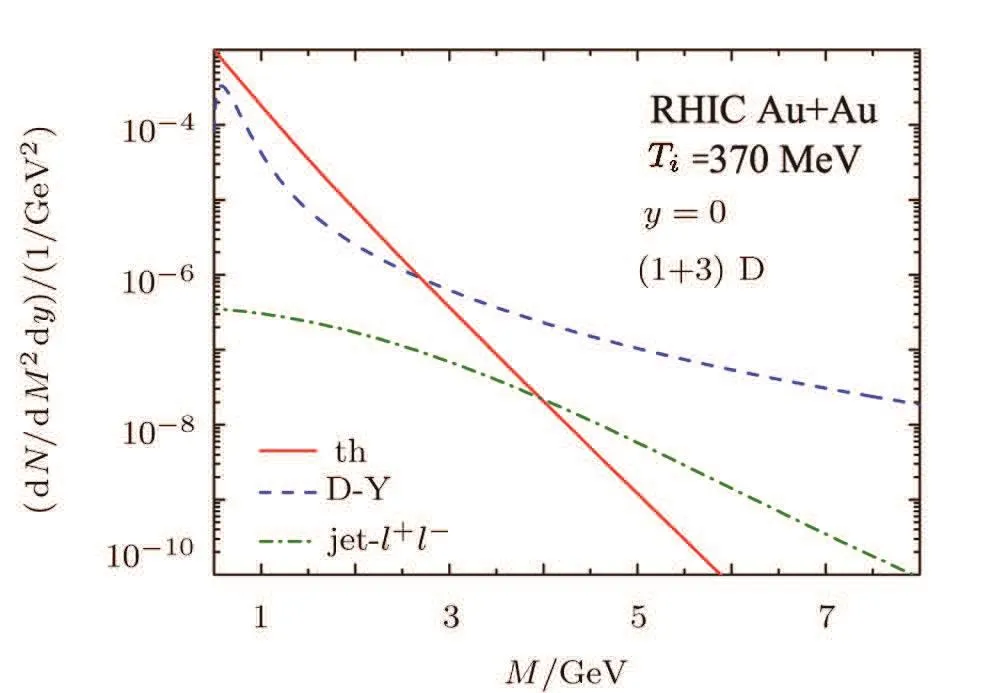



6 Summary
 Communications in Theoretical Physics2016年12期
Communications in Theoretical Physics2016年12期
- Communications in Theoretical Physics的其它文章
- Pressure Oscillating Flow in Corrugated Parallel Channel?
- Strong Decays of Charm Mesons (2680),(2760),(3000)?
- The Role of a1(1260)in π?p →(1260)p and π?p → π?ρ0p Reactions Near Threshold?
- Free Convective Nonaligned Non-Newtonian Flow with Non-linear Thermal Radiation
- Weibel Instability Growth Rate in Magnetized Plasmas with Quasi-Relativistic Distribution Function
- Quantum Private Comparison of Equality Based on Five-Particle Cluster State?
