ENDOMORPHISM ALGEBRAS IN THE YETTER-DRINFEL'D MODULE CATEGORY OVER A REGULAR MULTIPLIER HOPF ALGEBRA
YANG Tao,LIU Guang-jin,ZHOU Xuan
(1.School of Science,Nanjing Agricultural University,Nanjing 210095,China)
(2.School of Veterinary Medicine,Nanjing Agricultural University,Nanjing 210095,China)
(3.School of Mathematics and Information Technology,Jiangsu Second Normal University, Nanjing 210013,China)
ENDOMORPHISM ALGEBRAS IN THE YETTER-DRINFEL'D MODULE CATEGORY OVER A REGULAR MULTIPLIER HOPF ALGEBRA
YANG Tao1,LIU Guang-jin2,ZHOU Xuan3
(1.School of Science,Nanjing Agricultural University,Nanjing 210095,China)
(2.School of Veterinary Medicine,Nanjing Agricultural University,Nanjing 210095,China)
(3.School of Mathematics and Information Technology,Jiangsu Second Normal University, Nanjing 210013,China)
Endomorphism algebras in Yetter-Drinfel’d module category over a regular multiplier Hopf algebra are studied in this paper.By the tools of multiplier Hopf algebra and Homological algebra theories,we get that two endomorphism algebras are isomorphic in the Yetter-Drinfel’d module category,which generalizes the results of Panaite et al.in Hopf algebra case.
multiplier Hopf algebra;Yetter-Drinfel’d module;Yetter-Drinfel’d module category
2010 MR Subject Classification:16T05;16T99
Document code:AArticle ID:0255-7797(2016)06-1111-09
1 Introduction
Multiplier Hopf algebra,introduced by Van Daele[1],can be naturally considered as a generalization of Hopf algebra when the underlying algebra is no longer assumed to have a unit.Yetter-Drinfel'd module category,as an important content in Hopf algebras theory, was also studied by Van Daele and his collaborators.All the objects they discussed are (non-degenerate)algebras(see[2]).
However,in the well-known Hopf algebras case,the objects of Yetter-Drinfel'd module category are only vector spaces satisfying some certain conditions.So in[3],the authors gave a new category structure for regular multiplier Hopf algebra A:(α,β)-Yetter-Drinfel'd module categoryAyDA(α,β),in which the objects were vector spaces,generalizing the former notions.
In this paper,we focus our work on(α,β)-Yetter-Drinfel'd module,mainly consider some algebras in Yetter-Drinfel'd modules category and get some isomorphisms.
The paper is organized in the following way.In Section 2,we recall some notions which we will use in the following,such as multiplier Hopf algebras,modules and complete modules for a multiplier Hopf algebras,comodules and(α,β)-Yetter-Drinfel'd modules.
In Section 3,we consider algebras inAyDA(α,β).Let α,β∈Aut(A),and M∈AyDA(α,β)be finite dimensional.Consider the object M'∈AyDA(αβ-1α,α),coinciding with M as left A-modules,and having a right A-comodule structure given by

2 Preliminaries
Throughout this paper,all spaces we considered are over a fixed field k.We consider A as an algebra with a nondegenerate product,it is possible to construct the multiplier algebra M(A).M(A)is an algebra with identity such that A sits in M(A)as an essential two-sided ideal,it can be also characterized as the largest algebra with identity containing A as an essential ideal.More details about the concept of the multiplier algebra of an algebra,we refer to[1].
An algebra morphism(or homomorphism)?:A-→M(A?A)is called a comultiplication on A if(a?b)=?(a)(1?b)and(a?b)=(a?1)?(b)are elements of A?A for all a,b∈A and if?is coassociative in the sense that the linear mappings:A?A-→A?A obey the relation where id denotes the identity map.
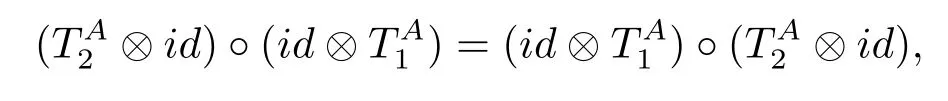
A pair(A,?)of an algebra A with nondegenerate product and a comultiplication?on A is called a multiplier Hopf algebra ifandare bijective(see[1]),(A,?)is regular if and only if the antipode of(A,?cop)is bijective.
Let(A,?,ε,S)be a regular multiplier Hopf algebra and M a vector space.Then M is called a(left-right)(α,β)-Yetter-Drinfel'd module over regular multiplier Hopf algebra A,if
(1)(M,·)is a left unital A-module,i.e.,A·M=M.
(2)(M,Γ)is a(right)A-comodule,where Γ:M→M0(M?A)denotes the right coaction of A on M,M0(M?A)denote the completed module.
(3)Γ and·satisfy the following compatible conditions
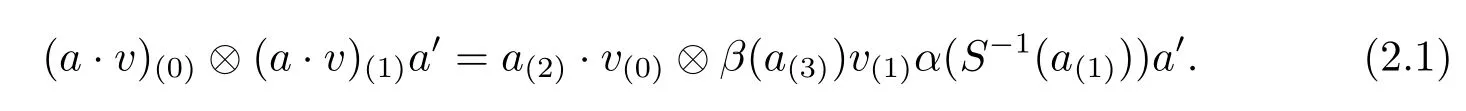
By the definition of Yetter-Drinfel'd modules,we can define(left-right)Yetter-Drinfel'd module categoryAyDA(α,β).The other three Yetter-Drinfel'd module categories are similar (more details see[3-5]).
AyDA(id,id)=AyDA,the left-right Yetter-Drinfel'd module category.
3 Endomorphism Algebras
Let A be a regular multiplier Hopf algebra,in this section,we mainly consider(left-right) Yetter-Drinfel'd module categoryAyDAover regular multiplier Hopf algebra A.
Definition 3.1 Let A be a multiplier Hopf algebra and C a unital algebra.C is called a left A-module algebra,if
(1)(C,·)is a left unital A-module,
(2)the module action satisfies

C is called right A-comodule algebra,if
(1)(C,ρ)is a right A-comodule,
(2)the comodule structure map ρ satisfies:for all a∈A,
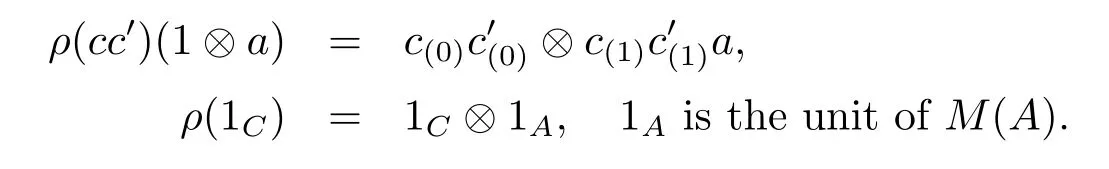
Let C be a unital associative algebra inAyDA.That means C is an object inAyDA, and the multiplication C?C→C and a unit map ι:k→C satisfying associativity and unit axioms.
Proposition 3.2 C is a unital algebra inAyDAif and only if C is an object inAyDAand C is a left A-module algebra and a right Aop-comodule algebra.
We denote by Copthe usual opposite algebra,with the multiplication c·c'=c'c for all c,c'∈C,and bythe A-opposite algebra,which means C as an object inAyDA,but with the multiplicationfor all c,c'∈C,i.e.,the opposite of C in the categoryAyDA.
Proposition 3.3 By above notation,if C is an algebra inAyDA,thenis an algebra inAyDA.
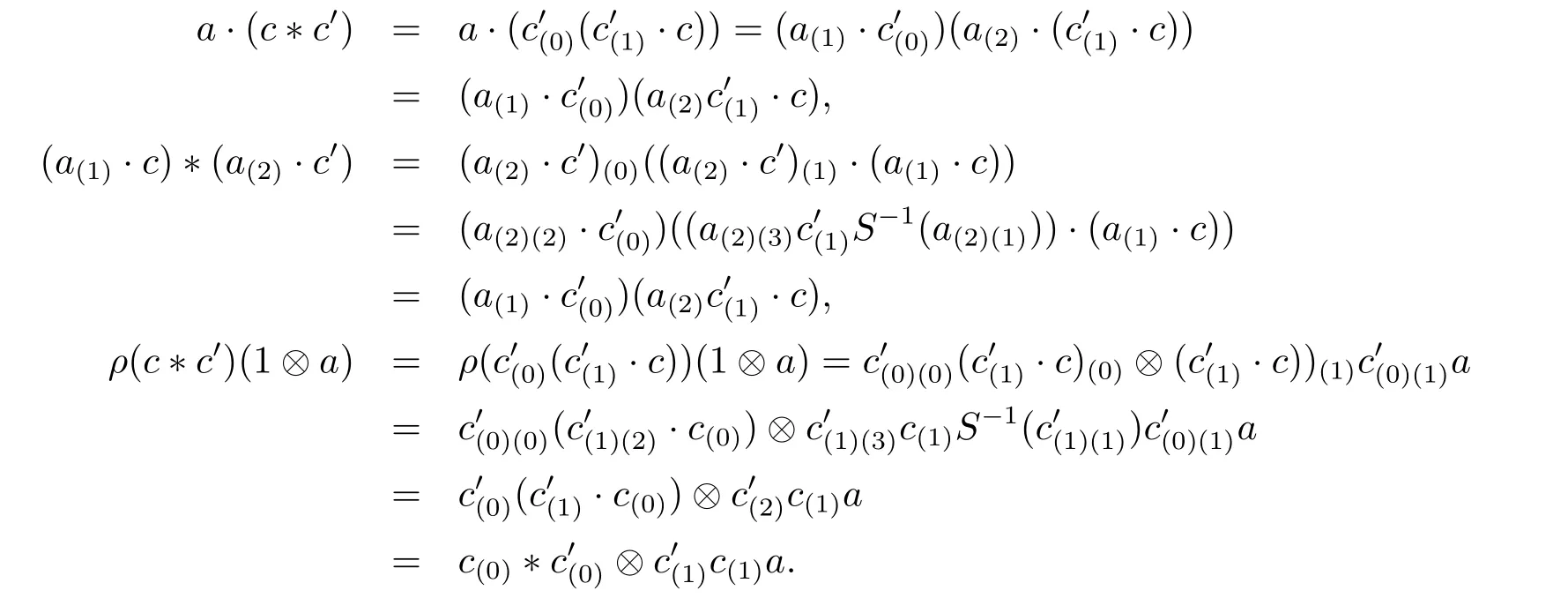
Proposition 3.4 If C,D are algebras inAyDA,then C?D is also an algebra inAyDAwith the following structures
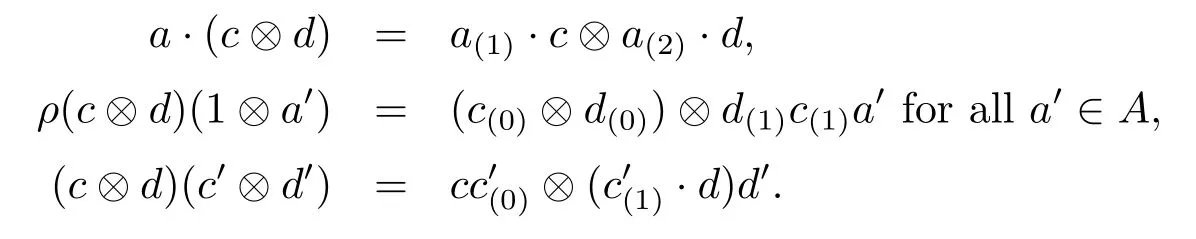
Proof It is obvious.Indeed,this algebra structure on C?D given above is just the braided tensor product of C and D in the braided tensor categoryAyDA.
We now introduce the endomorphism algebras associated to(α,β)-Yetter-Drinfel'd modules.
Proposition 3.5 Let α,β∈Aut(A)and M∈AyDA(α,β)be finite dimensional.Then
(1)End(M)is an algebra inAyDAwith structures
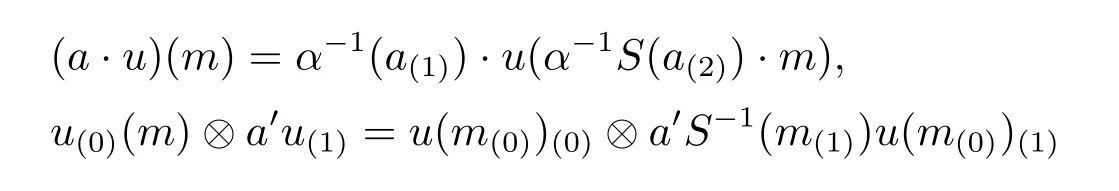
for all a,a'∈A,u∈End(M)and m∈M.
(2)End(M)opis an algebra inAyDAwith structures
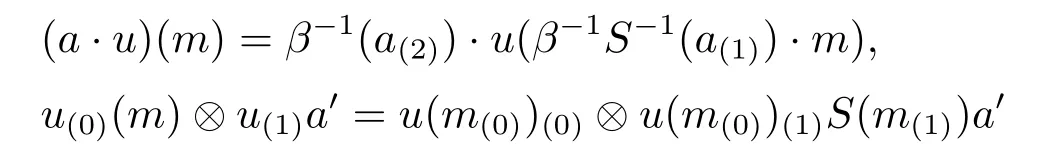
for all a,a'∈A,u∈End(M)opand m∈M.
Proof We only prove(1)here,(2)is similar.For(1),we first show that End(M)is an object inAyDA.In the following,we show the main process:the compatible condition ofAyDA,i.e.,

It holds,since
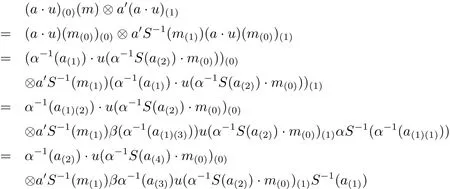
and
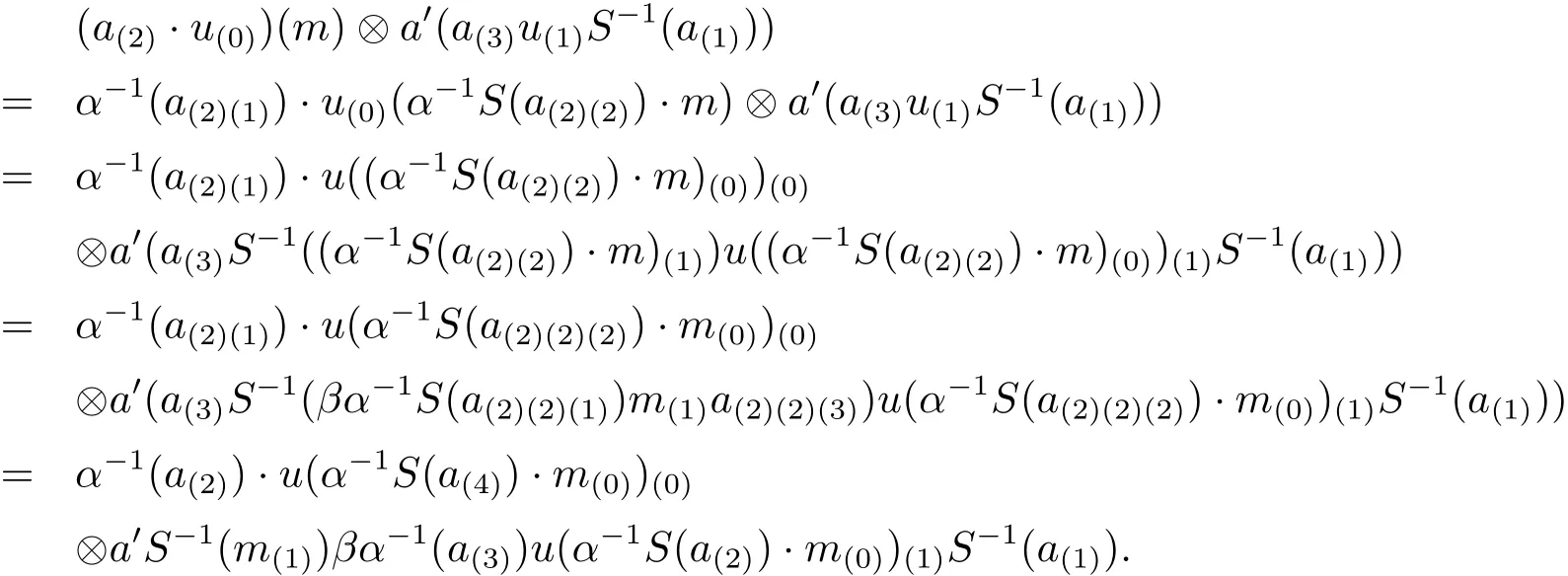
Then we need to show that the product defined in(1)is A-linear and A-colinear.
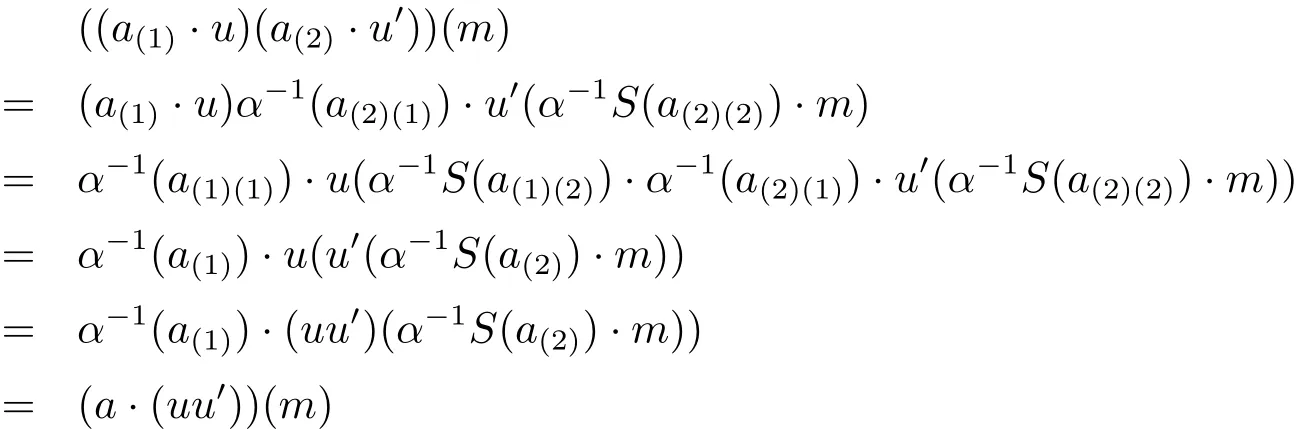
and
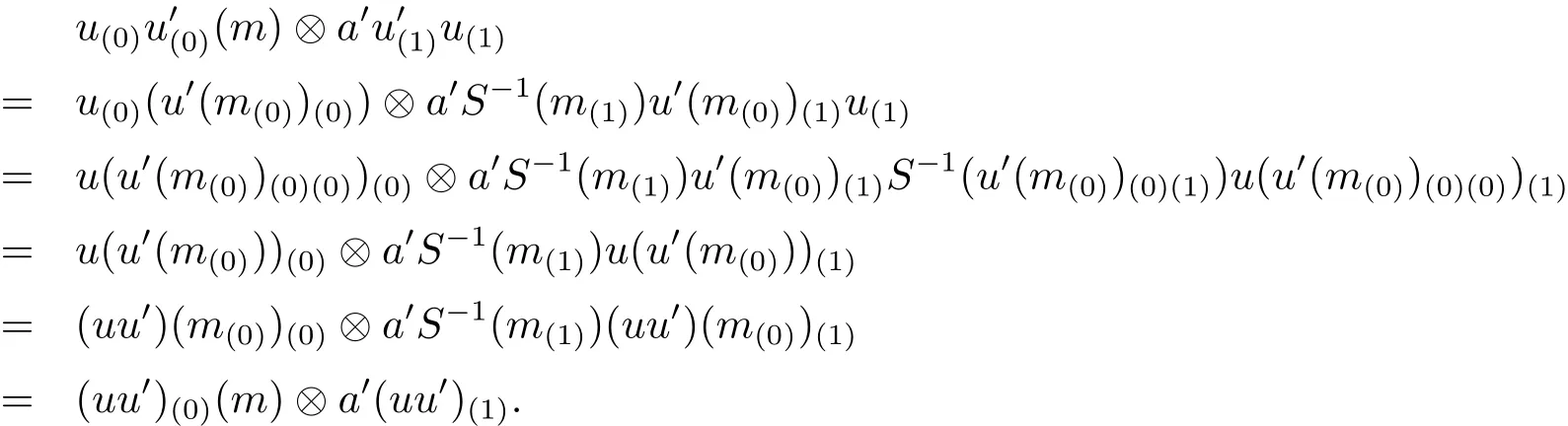
It is easy to get a·id=ε(a)id and ρ(id)=id?1,where id is the unit in End(M).This completes the proof.
Remark here that
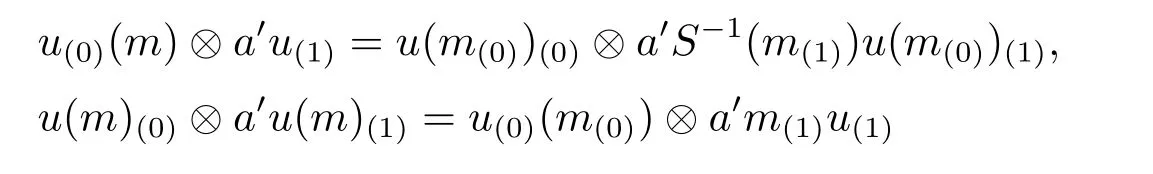
are equivalent.
Proposition 3.6 Let α,β∈Aut(A),and M∈AyDA(α,β).Define a new object M'as follows:M'coincides with M as left A-modules,and has a right A-comodule structure
given by
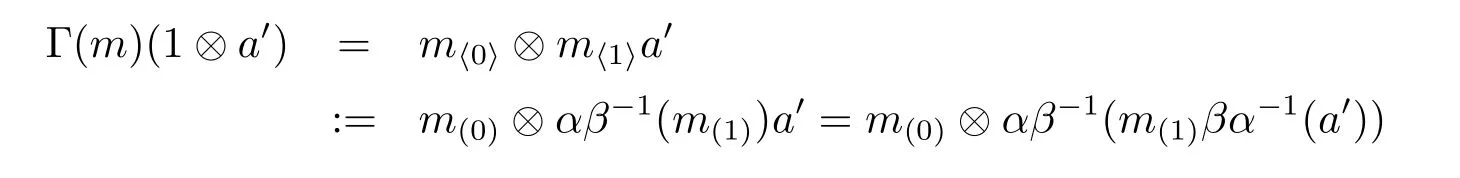
for all a'∈A and m∈M,where
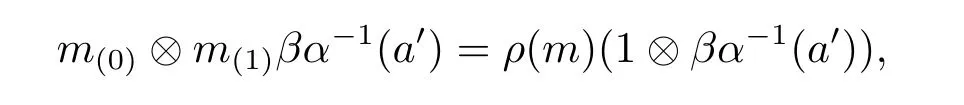
and ρ is the comodule structure of M.Then
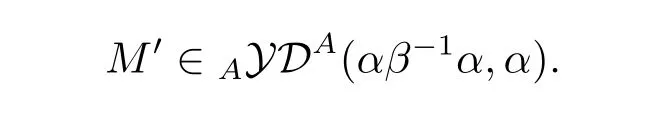
Proof We can get the conclusion by direct computation.

this implies M'∈AyDA(αβ-1α,α).
Theorem 3.7 Let α,β∈Aut(A),and M∈AyDA(α,β)be finite dimensional.Consider the object M'∈AyDA(αβ-1α,α)as above.Define the map
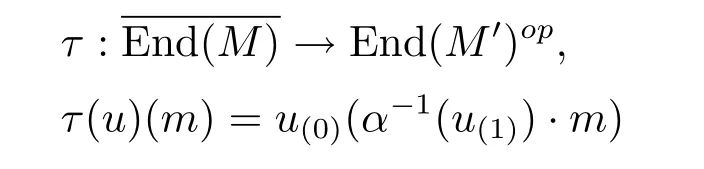
for all u∈End(M)and m∈M'.Then τ is an isomorphism of algebras inAyDA.
Proof Similar to the proof of Proposition 4.10 in[6].
First,τ is a homomorphism,since for u,v∈End(M),
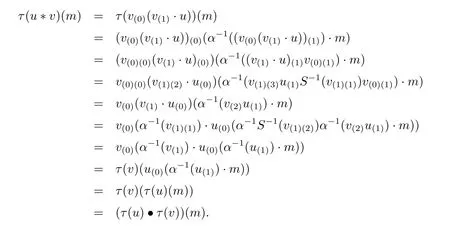
Second,τ is A-linear,since
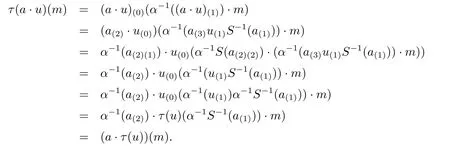
Third,τ is A-colinear.To prove this,we have to show that ρτ=(τ?l)ρ,where ρ is the A-comodule structure of End(M')op.Denote ρ(v)(1?a)=v(0)?v(1)a,we have to prove
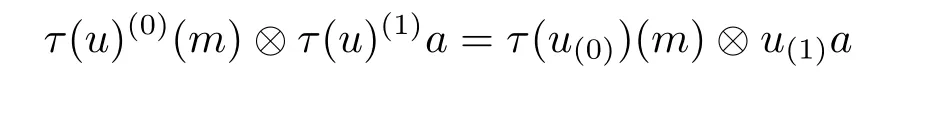
for all a∈A,
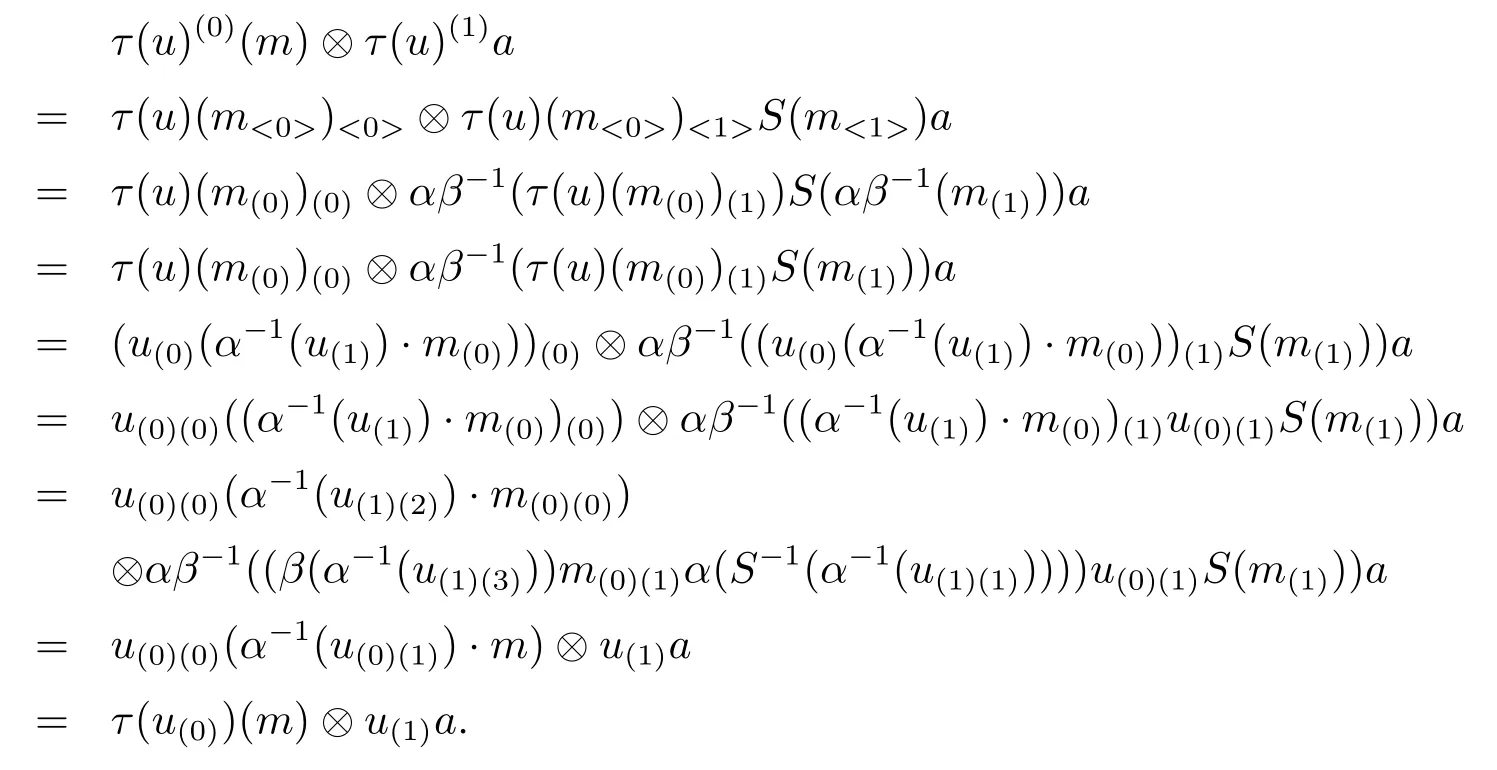
Finally,we will show that τ is bijective,we define
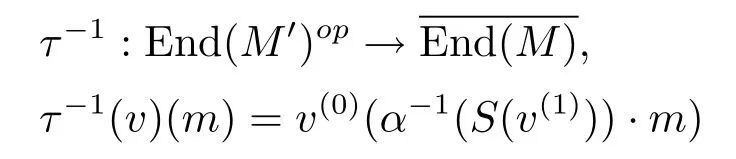
for v∈End(M')op.We can check that ττ-1=τ-1τ=id and τ-1is A-linear and A-colinear.
This completes the proof.
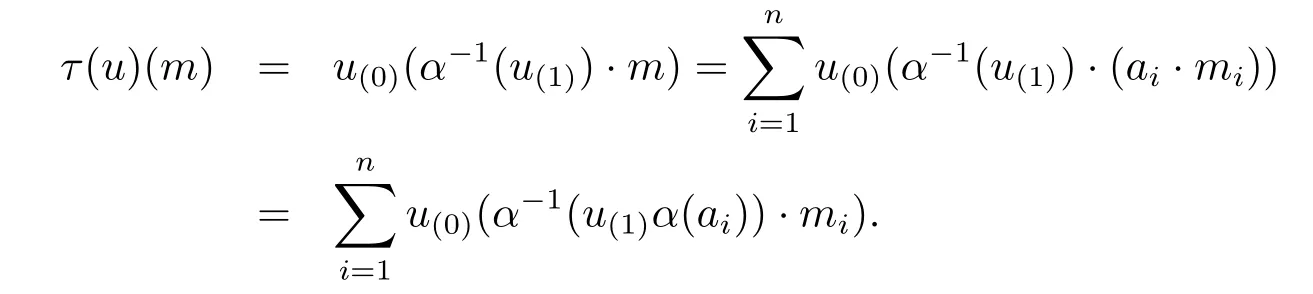
The definition of τ is meaningful.Because for finite i,there is an e∈A such that eai=aifor all i=1,···,n.Here
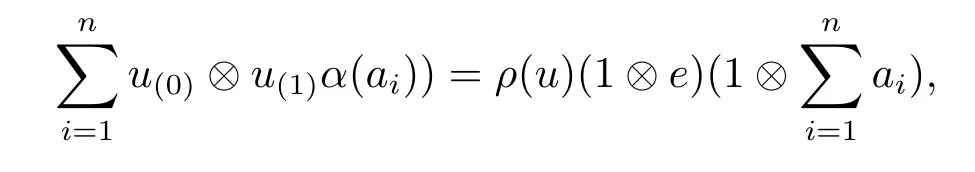
where ρ is the right A-comodule structure of End(M).
From Proposition 3.5 and the notion◇M defined in Section 3 of[5],we can get the following results:
Proposition 3.8 Let α,β∈Aut(A),and M∈AyDA(α,β)be finite dimensional.Then End(M)opEnd(◇M)as algebras inAyDA.
Proof Denote the map ?:End(M)op-→End(◇M)by ?(u)=u?for u∈End(M)op.It is an algebra isomorphism.
The map ? is A-linear,the proof is similar as in Proposition 4.11 in[6].Then we need to show ? is A-colinear.Indeed,by Proposition 3.5 and the structures of◇M,we can compute as follows:for all u∈End(M)op,f∈◇M,m∈M,and a∈A,

and
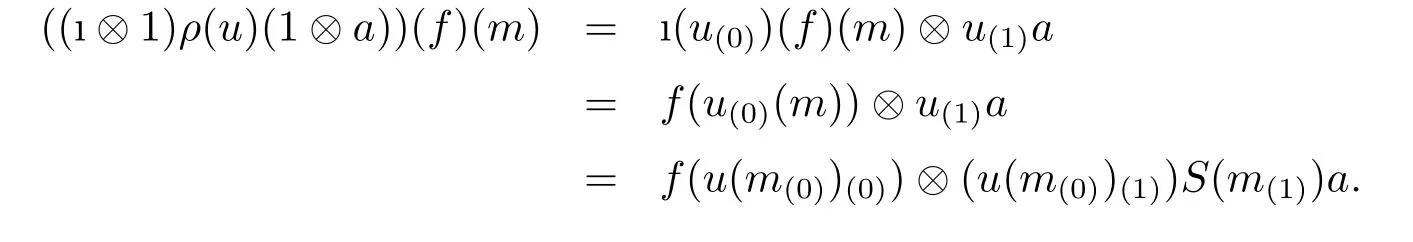
From all above,we use the adapted Sweedler notation,it seems that the definitions and proofs are similar as in the(weak)Hopf algebra case(see,e.g.[7]).However,we should notice the‘cover’technique introduced in[8].
References
[1]Van Daele A.Multiplier Hopf algebras[J].Trans.American Math.Soc.,1994,342(2):917-932.
[2]Delvaux L.Yetter-Drinfel’d modules for group-cograded multiplier Hopf algebras[J].Commun.Algebra,2008,36(8):2872-2882.
[3]Yang T,Wang S H.Constructing new braided T-categories over regular multiplier Hopf algebras[J]. Commun.Algebra,2011,39(9):3073-3089.
[4]Delvaux L,Van Daele A,Wang Shuanhong.Bicrossproducts of multiplier Hopf algebras[J].J.Algebra,2011,343(1):11-36.
[5]Yang T,Zhou X,Ma T S.On braided T-categories over multiplier Hopf algebras[J].Commun. Algebra,2013,41(8):2852-2868.
[6]Panaite F,Van Oystaeyen F.Quasi-elementary H-Azumaya algebras arising from generalized(anti) Yetter-Drinfel’d modules[J].Appl.Categ.Struct.,2009,19(5):803-820.
[7]Zhou X,Yang T.Kegel’s theorem over weak Hopf group coalgebras[J].J.Math.,2013,33(2):228-236.
[8]Van Daele A.Tools for working with multiplier Hopf algebras[J].Arabian J.Sci.Engin.,2008, 33(2C):505-527.
正則乘子Hopf代數(shù)上Yetter-Drinfel'd模范疇中的自同構(gòu)代數(shù)
楊濤1,劉廣錦2,周璇3
(1.南京農(nóng)業(yè)大學(xué)理學(xué)院,江蘇南京210095)
(2.南京農(nóng)業(yè)大學(xué)動物醫(yī)學(xué)院,江蘇南京210095)
(3.江蘇第二師范學(xué)院數(shù)學(xué)與信息技術(shù)學(xué)院,江蘇南京210013)
本文研究了正則乘子Hopf代數(shù)上Yetter-Drinfel’d模范疇中自同構(gòu)代數(shù)的問題.利用乘子Hopf代數(shù)以及同調(diào)代數(shù)理論中的方法,獲得了Yetter-Drinfel’d模范疇中兩個自同構(gòu)代數(shù)是同構(gòu)的結(jié)果,推廣了Panaite等人在Hopf代數(shù)中的結(jié)果.
乘子Hopf代數(shù);Yetter-Drinfel’d模;Yetter-Drinfel’d模范疇
MR(2010)主題分類號:16T05;16T99O153.3
?date:2014-03-24Accepted date:2014-11-11
Supported by National Natural Science Foundation of China(11226070; 11326063).
Biography:Yang Tao(1984-),male,born at Huaian,Jiangsu,doctor,major in Hopf algebras.
- 數(shù)學(xué)雜志的其它文章
- COMPLETE MOMENT CONVERGENCE OF WEIGHTED SUMS FOR ARRAYS OF DEPENDENT RANDOM VARIABLES
- CHEN-RICCI INEQUALITIES FOR SUBMANIFOLDS OF GENERALIZED COMPLEX SPACE FORMS WITH SEMI-SYMMETRIC METRIC CONNECTIONS
- ON CONFORMABLE NABLA FRACTIONAL DERIVATIVE ON TIME SCALES
- BOUNDEDNESS FOR SOME SCHRDINGER TYPE OPERATORS ON MORREY SPACES WITH VARIABLE EXPONENT RELATED TO CERTAIN NONNEGATIVE POTENTIALS
- STABILITY AND HOPF BIFURCATION OF A PREDATOR-PREY BIOLOGICAL ECONOMIC SYSTEM
- GROUND STATE SOLUTIONS FOR NONLINEAR DIFFERENCE EQUATIONS WITH PERIODIC COEFFICIENTS

