王玉雷,劉合國,吳佐慧

(1.河南工業(yè)大學(xué)數(shù)學(xué)系,河南鄭州450001)

(2.湖北大學(xué)數(shù)學(xué)系,湖北武漢430062)

一類中心循環(huán)的有限p-群的自同構(gòu)群的研究

王玉雷1,劉合國2,吳佐慧2

(1.河南工業(yè)大學(xué)數(shù)學(xué)系,河南鄭州450001)

(2.湖北大學(xué)數(shù)學(xué)系,湖北武漢430062)

本文研究了一類中心循環(huán)的有限p-群G的自同構(gòu)群.利用在G的導(dǎo)群上作用平凡的自同構(gòu)以及環(huán)上的辛群和正交群,確定了G的自同構(gòu)群的結(jié)構(gòu),這推廣了Bornand的相應(yīng)結(jié)果.

有限p-群;循環(huán)中心;辛空間;自同構(gòu)群

1　引言和預(yù)備知識

文中p是一個(gè)素?cái)?shù),采用的術(shù)語和符號都是標(biāo)準(zhǔn)的,參照文獻(xiàn)[1].

設(shè)G1和G2是任意兩個(gè)群,并且Z1和Z2分別是G1和G2的中心子群,假設(shè)Z1和Z2是同構(gòu)的,設(shè)θ:Z1→Z2是同構(gòu)映射,稱G1?G2是G1和G2相對于Z1,Z2和θ的中心積,即G1?G2是G1×G2關(guān)于正規(guī)子群{(z1,θ(z1)-1)|z1∈Z1}的商群.特別地,設(shè)G是任意一個(gè)群,中心積G?G是借助于中心上的恒等映射所得,為了方便,對于任意n＞1,用G?n標(biāo)記中心積G?(n-1)?G,G?1=G且G?0=1.

一個(gè)有限p-群G是超特殊的,如果G＇=FratG=ζG都是p階群.Winter[2]給出了超特殊p-群的自同構(gòu)群.在文[1]中,一個(gè)有限p-群G稱為廣義超特殊的,如果G的中心是循環(huán)群且導(dǎo)群是p階群.在文[3]中,確定了這種廣義超特殊p-群的自同構(gòu)群.顯然,廣義超特殊p-群的中心商群是初等Abel群并且冪零類是2,因此廣義超特殊p-群真包含在中心循環(huán)的,冪零類是2的,并且中心商群是齊次循環(huán)的有限p-群中,這樣一類有限p-群在文獻(xiàn)[4]中給出,即X3(pm)?n?Zpm+r,其中n≥1,m≥1和r≥0,且

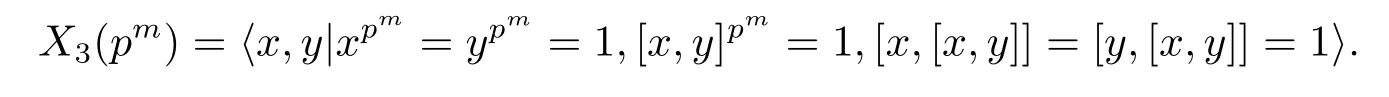
當(dāng)p是奇素?cái)?shù)時(shí),這類群的自同構(gòu)群被確定,即下面的命題.

命題1.1設(shè)p是一個(gè)奇素?cái)?shù),G=X3(pm)?n?Zpm+r,其中n≥1,m≥1和r≥0.假設(shè)

則Aut G=AutζGGAutζG,并且存在下面的正合列

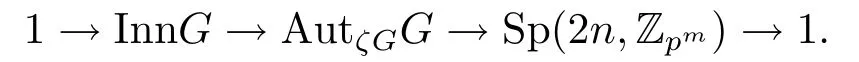
在本文中,當(dāng)p是奇素?cái)?shù)時(shí),借助導(dǎo)群的特點(diǎn),重新刻畫該類有限p-群的自同構(gòu)群,進(jìn)一步,確定這類有限2-群的自同構(gòu)群.若m=1,則該類群是廣義超特殊p-群.為了不至于重復(fù)文獻(xiàn)[3]中廣義超特殊p-群的結(jié)果,只考慮m≥2的情況,所得主要結(jié)果如下.

定理A設(shè)p是一個(gè)奇素?cái)?shù),G=X3(pm)?n?Zpm+r,其中m≥2,n≥1和r≥0.設(shè)AutG＇G={α∈Aut G|α在G＇上作用平凡},則

(i)Aut G/AutG＇GZpm-1(p-1).

(ii)AutG＇G/InnGSp(2n,Zpm)×Zpr.

定理B設(shè)G=X3(2m)?n?Z2m+r,其中m≥2,n≥1和r≥0.設(shè)AutG＇G={α∈Aut G|α在G＇上作用平凡},則

(i)Aut G/AutG＇GZ2m-2×Z2.

(ii)AutG＇G/InnGK×Z2r,其中K=Sp(2n,Z2m)(當(dāng)r＞0時(shí))或者O(2n,Z2m)(當(dāng)r=0時(shí)).

為了得到結(jié)果,需要下面的引理.

引理1.1設(shè)m和r都是正整數(shù),并且m≥2和r≥1.則

(i)(pm+1)pr=1(mod pm+r).

(ii)(pm+1)pr-1=1+pm+r-1(mod pm+r).

證根據(jù)二項(xiàng)式定理可得

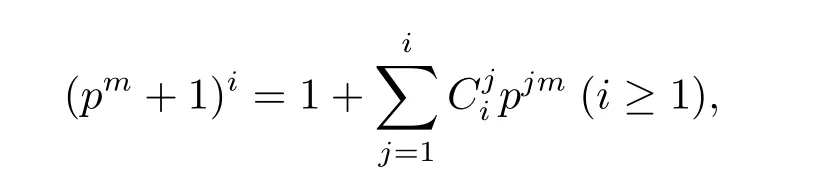
若j=1并且i=pr,則

若j=1并且i=pr-1,則

若j=2并且i=pr-1,則0(mod pm+r)(當(dāng)p是奇素?cái)?shù)時(shí))或者(2r-1-1)22m+r-2≡0(mod 2m+r)(當(dāng)p=2時(shí)).

假設(shè)j≥3并且i=pr-1.注意到j(luò)!=其中3≤j≤pr-1并且(n＇,p)=1.則

從而

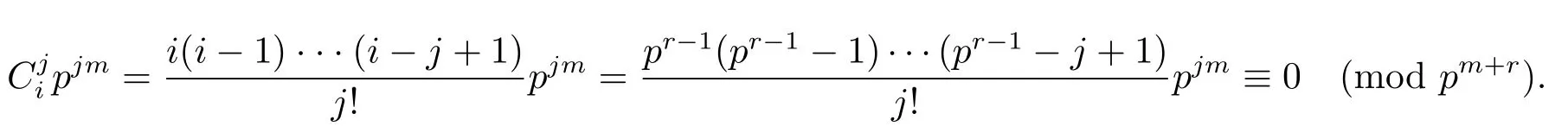
同理可得,若i=pr,則≡0(mod pm+r),其中j≥2.引理1.1得證.

2　定理A的證明

假設(shè)x1,x2,···,x2n-1,x2n,y是G的一組生成元,并且滿足

定理2.1 AutG＇G?Aut G并且Aut G/AutG＇GZpm-1(p-1).

證顯然AutG＇G?Aut G.由于p是一個(gè)奇素?cái)?shù),因此是一個(gè)循環(huán)群.設(shè)v是的一個(gè)生成元,定義映射

容易驗(yàn)證θ∈Aut G.任取α∈Aut G.因?yàn)镚＇=〈ypr〉,所以存在0＜v1＜pm并且(v1,p)=1使得α(ypr)=(ypr)v1.從而存在0＜v2＜pm使得vv2≡(mod pm).由于

因此θv2α∈AutG＇G.從而Aut G=〈θ〉A(chǔ)utG＇G.

如果θu∈〈θ〉∩AutG＇G,那么

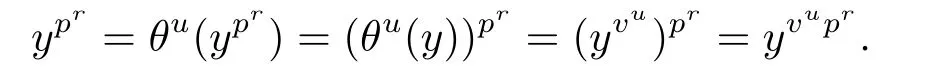
因此pr(vu-1)≡0(mod pm+r),即vu-1≡0(mod pm).從而pm-1(p-1)|u.顯然θpm-1(p-1)∈AutG＇G,這說明〈θ〉∩AutG＇G=〈θpm-1(p-1)〉.結(jié)果可得Aut G/AutG＇G〈θ〉/〈θpm-1(p-1)〉Zpm-1(p-1).定理2.1得證.

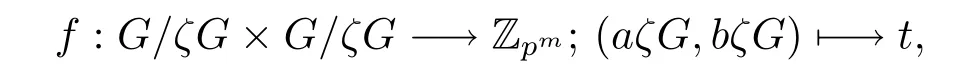
其中[a,b]=(ypr)t,0≤t＜pm.容易驗(yàn)證f是一個(gè)交錯(cuò)雙線性型.令i:=xiζG,顯然, G/ζG的一組基1,2,···,2n-1,2n滿足

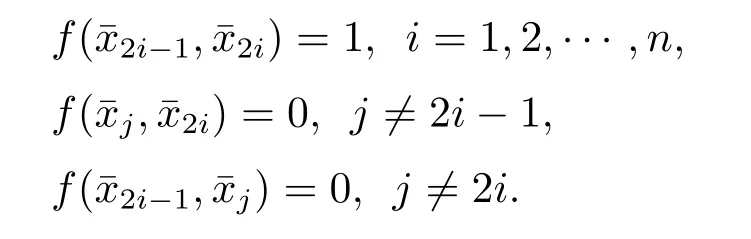
設(shè)Ψ:AutG＇G-→Aut(G/ζG)和Φ:AutG＇G-→AutζG是自然誘導(dǎo)同態(tài).定義一個(gè)同態(tài)映射

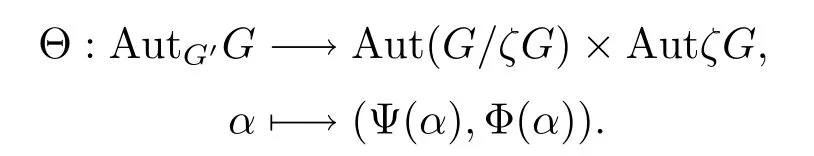
對于任意α∈AutG＇G,有[α(a),α(b)]=α[a,b]=[a,b],其中a,b∈G,從而

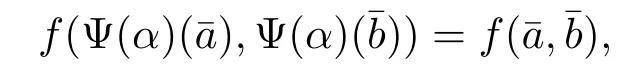
定理2.2 KerΘ=InnG.

證顯然,InnG≤KerΘ.任取α∈KerΘ,假設(shè)α(xi)=xiysi,α(y)=y,其中0≤si＜pm+r,i=1,2,···,2n.由于

因此pr|si.從而|KerΘ|≤p2nm.顯然|InnG|=p2nm,因此KerΘ=InnG.定理2.2得證.

定理2.3 ImΨ=Sp(2n,Zpm).

證任取T∈Sp(2n,Zpm).設(shè)T在G/ζG的一組基{i|i=xiζG,i=1,2,···,2n}上對應(yīng)的矩陣是A=(aij).

定義映射

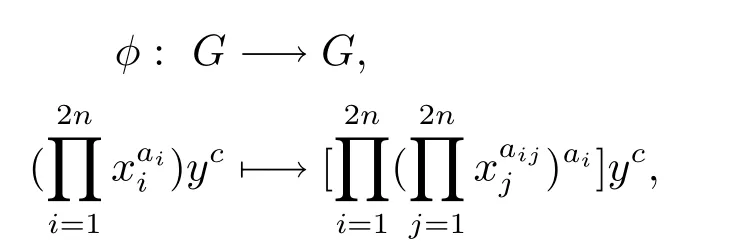
其中0≤ai＜pm,i=1,2,···,2n,0≤c＜pm+r.

注意到(aij)是一個(gè)非奇異矩陣.容易驗(yàn)證φ是一個(gè)雙射.因此φ是G的一個(gè)自同構(gòu)當(dāng)且僅當(dāng)φ是一個(gè)同態(tài)映射.根據(jù)φ的定義,下面的結(jié)論成立.

(4)φ(y)=y,

稱上面的φ是T在G上的誘導(dǎo)映射.

任意g1,g2∈G,假設(shè)g1=則

其中ye=

設(shè)ai+bi=ri+pmsi且e=t1+tpm+r,其中0≤ri＜pm,si∈Z,0≤t1＜pm+r,t∈Z,則

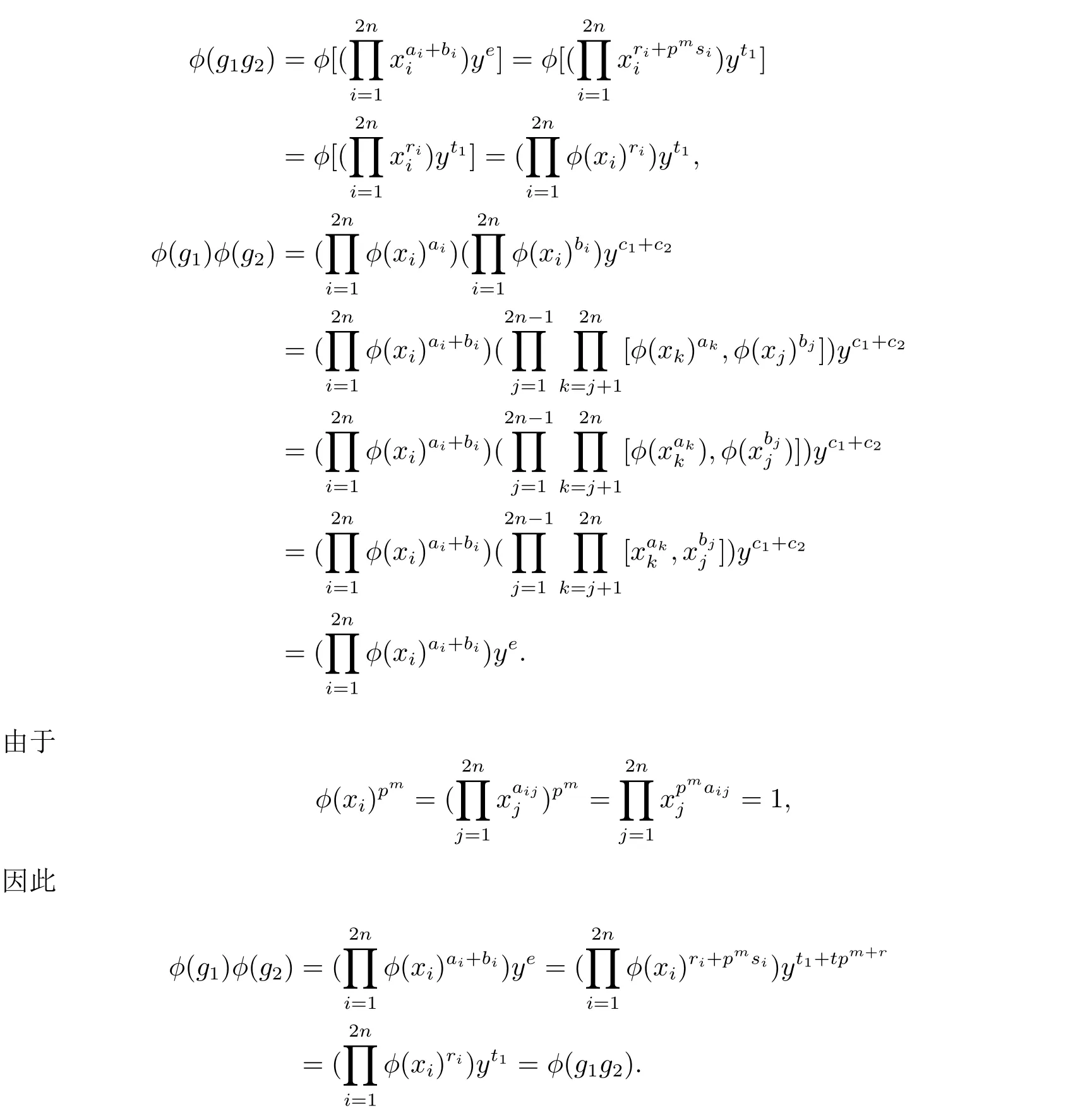
從而φ∈AutG＇G,并且Ψ(φ)=T.結(jié)果可得ImΨ=Sp(2n,Zpm).定理2.3得證.

證定義映射

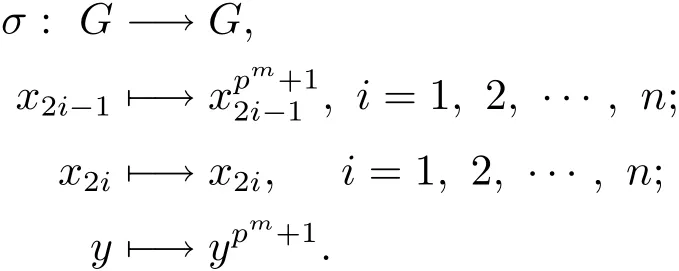
容易驗(yàn)證σ是G的一個(gè)自同構(gòu).因?yàn)镚＇=〈ypr〉和σ(ypr)=σ(y)pr=(ypm+1)pr=ypr,所以σ∈AutG＇G.

若r=0,則ζG=G＇,那么σ是恒等自同構(gòu).下面不妨假設(shè)r＞0.

由引理1.1可得(pm+1)pr≡1(mod pm+r)和(pm+1)pr-1≡1+pm+r-1(mod pm+r).由于

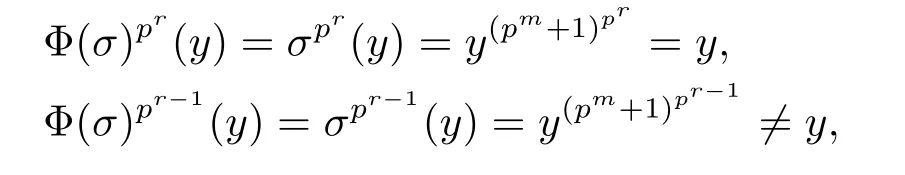
因此Φ(σ)的階是pr.

任取α∈AutG＇G,則α(ypr)=ypr.設(shè)α(y)=yu,其中0≤u＜pm+r.因?yàn)閥pr= α(ypr)=α(y)pr=yupr,所以pm+r|pr(u-1),即pm|(u-1).設(shè)u=1+pmu＇,其中u＇∈Z.根據(jù)引理1.1,容易驗(yàn)證upr=(1+pmu＇)pr≡1(mod pm+r),因此Φ(α)pr(y)=αpr(y)= yupr=y,這表明Φ(α)是一個(gè)p-元素,從而ImΦ是一個(gè)冪指數(shù)為pr的p-群.由于AutζG是pm+r-1(p-1)階循環(huán)群,從而ImΦ=〈Φ(σ)〉Zpr.定理2.4得證.

3　定理B的證明

假設(shè)x1,x2,···,x2n-1,x2n,y是G的一組生成元,并且滿足

定理3.1 AutG＇G?Aut G并且Aut G/AutG＇GZ2m-2×Z2.

證由于G＇=〈y2r〉,因此AutG＇Z?

2m.由AutG到AutG＇的誘導(dǎo)同態(tài)可得AutG/AutG＇G同構(gòu)于的一個(gè)子群.根據(jù)Z2m-2×Z2,假設(shè)Z?2m=〈r1〉×〈r2〉,其中r1:=3和r2:=2m-1的階分別是2m-2和2.

定義映射

和

容易驗(yàn)證θ1和θ2都是G的自同構(gòu).

如果m=2,那么θ1=θ2.任取α∈Aut G.因?yàn)镚＇=〈y2r〉,所以存在0＜t＜4并且(t,2)=1使得α(y2r)=(y2r)t.從而存在0＜t1＜4使得≡t-1(mod 4).由于

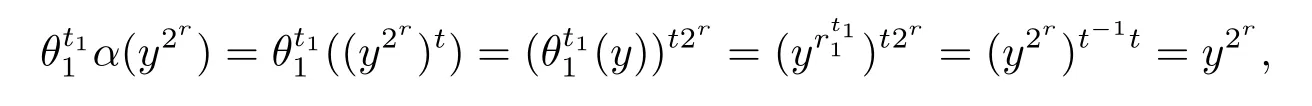
為了方便,不至于引起混淆,仍用定理A中的記號,定義同態(tài)映射

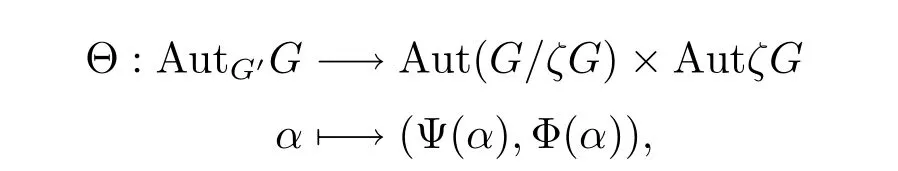
其中Ψ:AutG＇G-→Aut(G/ζG)和Φ:AutG＇G-→AutζG是自然誘導(dǎo)同態(tài).

根據(jù)定理2.2,同理可得KerΘ=InnG.

定理3.2若r＞0,則ImΨ=Sp(2n,Z2m).

證定義Z2m-模G/ζG上的交錯(cuò)雙線性型f:G/ζG×G/ζG-→Z2m;(aζG,bζG)t,其中[a,b]=(y2r)t,0≤t＜2m.根據(jù)定理A,同理可得ImΨ≤Sp(2n,Z2m).

任取T∈Sp(2n,Z2m).設(shè)T在G/ζG的一組基{i|i=xiζG,i=1,2,···,2n}上對應(yīng)的矩陣是A=(aij).

定義映射

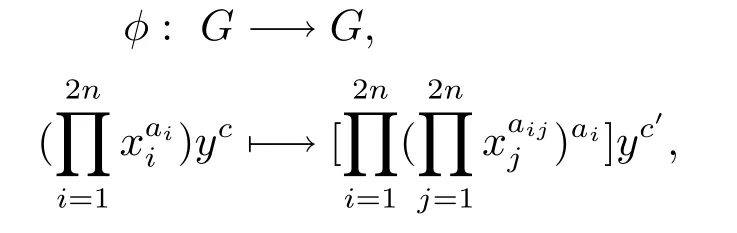
其中0≤ai＜2m,i=1,2,···,2n,0≤c＜2m+r,并且c＇≡c+(mod 2m+r).

注意到(aij)是一個(gè)非奇異矩陣.容易驗(yàn)證φ是一個(gè)雙射.因此φ是G的一個(gè)自同構(gòu)當(dāng)且僅當(dāng)φ是一個(gè)同態(tài)映射.根據(jù)φ的定義,下面的結(jié)論成立.

(4)φ(y)=y.

(5)

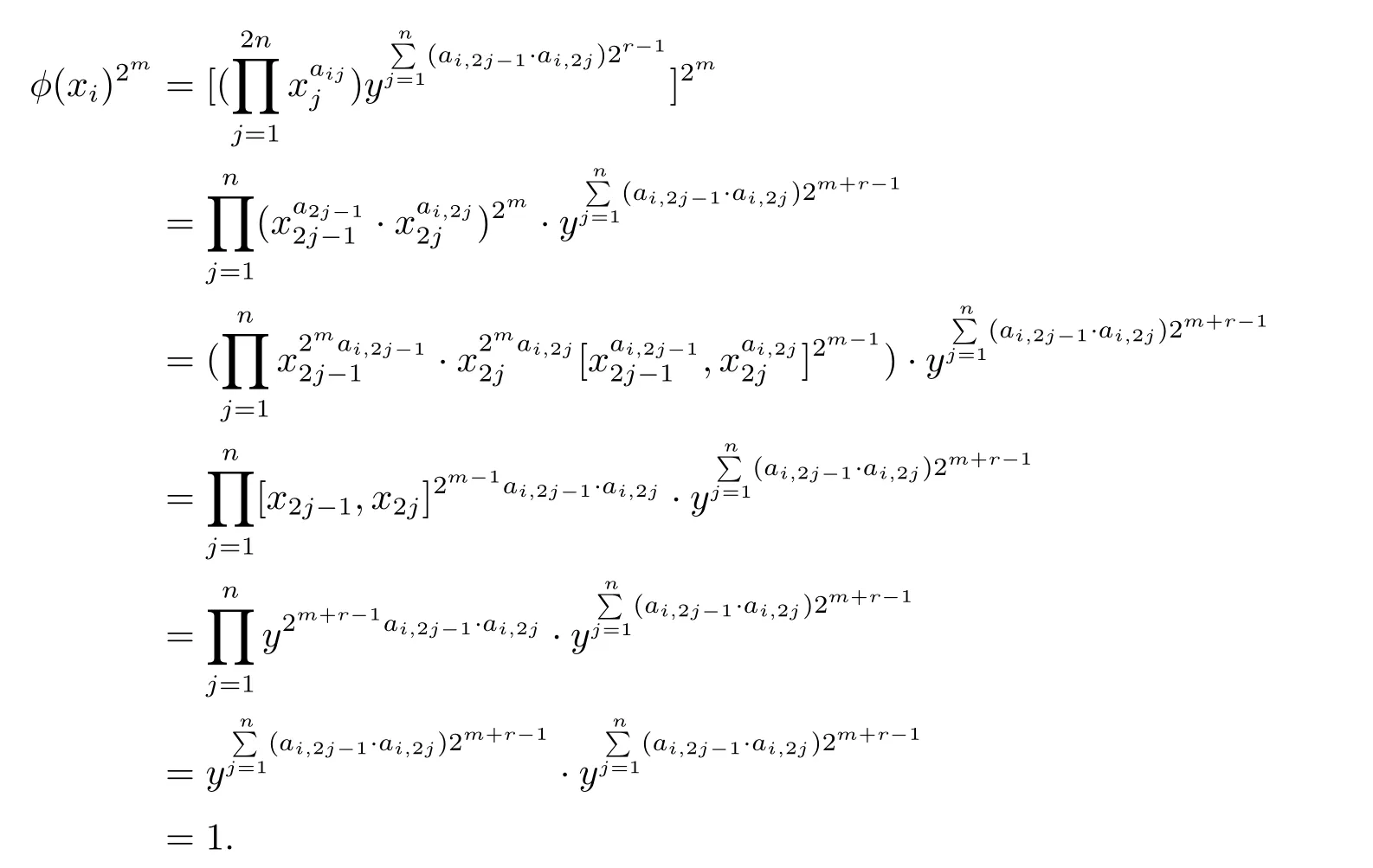
根據(jù)定理2.3的證明,同理可得φ∈AutG＇G,并且Ψ(φ)=T.結(jié)果可得ImΨ= Sp(2n,Z2m).定理3.2得證.

如果r=0,那么G=X3(2m)?n,此時(shí),G＇=ζG=〈y〉Z2m,在Z2m-模G/ζG上定義一個(gè)二次型,對任意:=xζG∈G/ζG,有

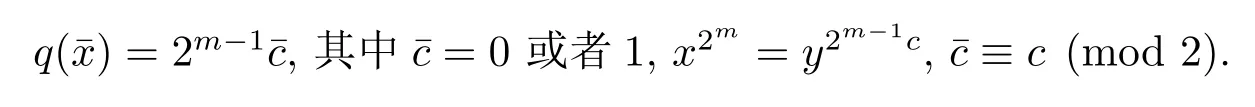
則有下面的定理.

定理3.3若r=0,則ImΨ=O(2n,Z2m).

證任意α∈AutG＇G,x∈G,則α(x)2m=α(x2m)=x2m,因此即 q(Ψ(α)())=q(),因此Ψ(α)∈O(2n,Z2m),由此可得ImΨ≤O(2n,Z2m).

任取T∈O(2n,Z2m).設(shè)T在G/ζG的一組基{i|i=xiζG,i=1,2,···,2n}上對應(yīng)的矩陣是A=(aij).

定義映射

其中0≤ai＜2m,i=1,2,···,2n,0≤c＜2m+r.

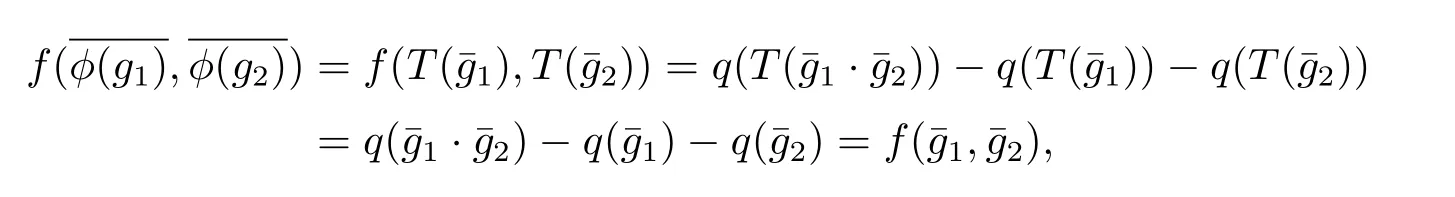
從而[φ(g1),φ(g2)]=[g1,g2].

類似于定理2.3的證明,同理可得φ∈AutG＇G,并且Ψ(φ)=T.總之,ImΨ= O(2n,Z2m).

證定義映射

容易驗(yàn)證σ1是G的一個(gè)自同構(gòu).因?yàn)镚＇=〈y2r〉和σ1(y2r)=σ1(y)2r=(y2m+1)2r=y2r,所以σ1∈AutG＇G.

由引理1.1可得(2m+1)2r≡1(mod 2m+r)和(2m+1)2r-1≡1+2m+r-1(mod 2m+r).

由于

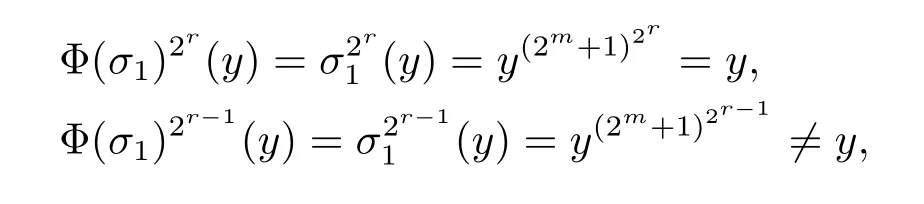
因此Φ(σ1)的階是2r.

任取α∈AutG＇G,則α(y2r)=y2r.設(shè)α(y)=yu,其中0≤u＜2m+r.因?yàn)閥2r= α(y2r)=α(y)2r=yu2r,所以2m+r|2r(u-1),即2m|(u-1).設(shè)u=1+2mu＇,其中u＇∈Z.從而Φ(α)(y)=y2mu＇+1,其中0≤u＇＜2r,因此|ImΦ|≤2r,結(jié)果可得ImΦ=〈Φ(σ1)〉Z2r.定理3.4得證.

[1]Robinson D J S.A course in the theory of groups(2nd ed.)[M].New York:Springer-Verlag,1996.

[2]Winter D.The automorphism group of an extraspecial p-group[J].Rocky Mountain J.Math.,1972, 2:159-168.

[3]Liu H G,Wang Y L.The automorphism group of a generalized extraspecial p-group[J].Sci.China Math.,2010,53(2):315-334.

[4]Bornand D.Elementary abelian subgroups in p-groups of class 2[D].Lausanne:cole Polytechnique Fdrale de Lausanne,2009.

[5]海進(jìn)科,王玉雷.有限群的Coleman外自同構(gòu)群是p＇-群的一些充分條件[J].數(shù)學(xué)雜志,2008,28(6): 653-658.

2010 MR Subject Classification:20E36;20F28

A STUDY ON THE AUTOMORPHISM GROUP OF A CLASS OF A FINITE P-GROUP WITH A CYCLIC CENTER

WANG Yu-lei1,LIU He-guo2,WU Zuo-hui2
(1.Department of Mathematics,Henan University of Technology,Zhengzhou 450001,China)
(2.Department of Mathematics,Hubei University,Wuhan 430062,China)

In this article,the automorphism group of a class of a finite p-group G with a cyclic center is researched.With the automorphisms which act trivially on the derived subgroup of G,symplectic group and orthogonal group over a ring,the structure of the automorphism group of G is determined,which generalizes the related results of Bornand.

finite p-group;cyclic center;symplectic space;automorphism group

MR(2010)主題分類號:20E36;20F28O152.3

A

0255-7797(2016)06-1273-10

?2015-08-27接收日期:2015-12-03

國家自然科學(xué)基金資助(11301150;11371124);河南省自然科學(xué)基金資助(142300410134; 162300410066).

王玉雷(1979-),男,河南南陽,副教授,博士,主要研究方向:代數(shù)學(xué).