YOU Mi-man,ZHOU Nan

(1.School of Mathematics and Information Science,North China University of Water Resource and Electric Power,Zhengzhou 450046,China )

(2.Department of Mathematics,Southeast University,Nanjing 211189,China )

DRINFELD DOUBLE FOR MONOIDAL HOM-HOPF GROUP-COALGEBRAS

YOU Mi-man1,ZHOU Nan2

(1.School of Mathematics and Information Science,North China University of Water Resource and Electric Power,Zhengzhou 450046,China )

(2.Department of Mathematics,Southeast University,Nanjing 211189,China )

In this paper,Drinfeld double over monoidal Hom-Hopf group-coalgebras is introduced.Via the definition of crossed monoidal Hom-Hopf T-coalgebras and the definition of quasitriangular monoidal Hom-Hopf group-coalgebras,we get the result that this Drinfeld double is a quasitriangular monoidal Hom-Hopf group-coalgebra.

quasitriangular;Monoidal Hom-Hopf group-coalgebra;Drinfeld Double

1 Introduction

Braided T-categories introduced by Turaev[1]are of interest due to their applications in homotopy quantum field theories,which are generalizations of ordinary topological quantum field theories.Braided crossed categories based on a group G,is braided monoidal categories in Freyd-Yetter categories of crossed G-sets(see[2])play a key role in the construction of these homotopy invariants.In[3],Zhou and Yang studied cotriangular weak Hopf groupcoalgebras and promoted Kegel theorem on the weak Hopf group-coalgebras.Motivated by this fact,Yang[4]introduced the notion of a monoidal Hom-group-coalgebra as a development of the notion of monoidal Hom-coalgebras in sense of Caenepeel and Goyvaerts(see [5]),and as a natural generalization of the notions of both the Hom-type Hopf algebras and the Hopf group-coalgebra in[1,6],and constructed a new kind of braided T-categories.

Starting from a finite-dimensional Hopf algebra H,Drinfeld[7]showed how to obtain a quasitriangular Hopf algebra D(H),the quantum double of H.It is now very natural to ask how to construct Drinfeld quantum double for finite-type monoidal Hom-Hopf groupcoalgebras.In this article,we essentially construct Drinfeld quantum double over monoidal Hom-Hopf group-coalgebras.

This article is organized as follows.In Section 1,we recall some notions and results about monoidal Hom-Hopf group-coalgebras.In Section 2,we construct the Drinfeld quantum double over monoidal Hom-Hopf group-coalgebras and study quasitriangular monoidal Hom-Hopf group-coalgebras.

2 Preliminaries

In this section,we recall the definitions and properties of monoidal Hom-Hopf algebras and monoidal Hom-Hopf group-coalgebras.Throughout this paper,we always let G be a discrete group with a neutral element 1 and k a field.If U and V are k-spaces,TU,V: U?V→V?U will denote the flip map defined by TU,V(u?v)=v?u for all u∈U and v∈V.

Definition 2.1(see[4])A monoidal Hom-G-coalgebra is a family of k-spaces C= {(Cα,ξCα)}α∈Gtogether with a family of k-linear maps Δ={Δα,β:Cαβ→Cα?Cβ}α,β∈Gand a k-linear map ε:C1→k,such that Δ is coassociative in the sense that

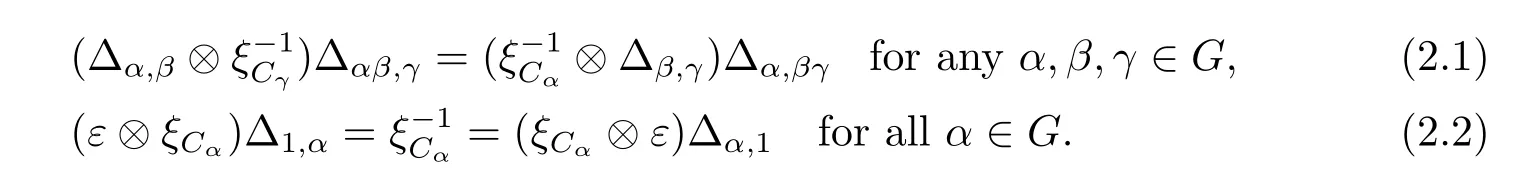
Remark 2.2(C1,ξC1,Δ1,1,ε)is a monoidal Hom-coaglegbra in the sense of Caenepeel and Goyvaerts[5].

Following the Sweedler’s notation for G-coalgebras,for any α,β∈G and c∈(Cαβ,ξCαβ) one writes

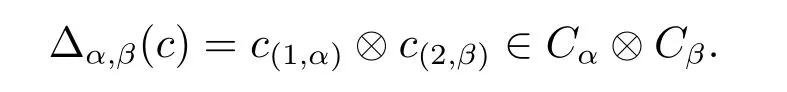
The coassociativity axiom(2.1)gives that,for any α,β,γ∈G and c∈(Cαβγ,ξCαβγ),

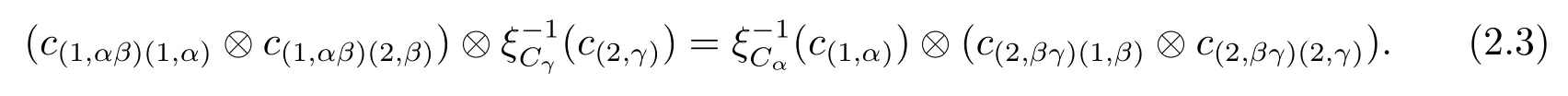
Definition 2.3(see[4])A monoidal Hom-Hopf G-coaglebra is a monoidal Hom-G-coalgebra H=({Hα,ξHα},Δ,ε)together with a family of k-linear maps S={Sα:Hα→Hα-1}α∈Gsuch that the following data holds:

Note that(H1,m1,11,Δ1,1,ε,S1)is a monoidal Hom-Hopf algebra.A monoidal Hom-Hopf G-coalgebra H is termed to be of finite type if,for all α∈G,Hαis finite-dimensional as k-vector space.

Remark 2.4Let H=({Hα,ξHα},Δ,ε,S)be a monoidal Hom-Hopf G-coalgebra. Suppose that the antipode S={Sα}α∈Gof H is bijective.For any α∈G,letbe the opposite algebra to Hα.Then Hop=endowed with the comultiplication andthe counit of H and with the antipodeis an opposite monoidal Hom-Hopf G-coalgebra of H.The coopposite monoidal Hom-G-coalgebra equipped with=Hα-1as an algebra and with the comultiplicationwith the antipode

Definition 2.5(see[4])A monoidal Hom-G-coalgebra H=({Hα,ξHα},Δ,ε,S)is said to be a monoidal Hom-T-coalgebra provided it is endowed with a family of algebra isomorphisms φ={φβ:Hα→Hβαβ-1}α,β∈Gsuch that each φβpreserves the comultiplication and the counit,i.e.,for all α,β,γ∈G,

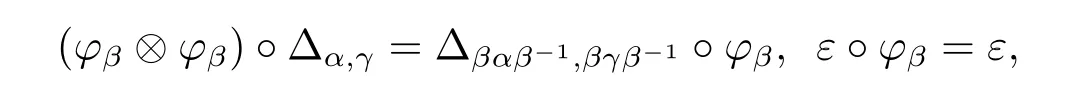
and φ is multiplicative in the sense that φαβ=φα?φβfor all α,β∈G.

Let H be a monoidal Hom-T-coalgebra.Then one has thatfor all α∈G and φ preserves the antipode,i.e.,φβ?Sα=Sβαβ-1?φβfor all α,β∈G.

3 The Drinfeld Quantum Double for Monoidal Hom-Hopf T-Coalgebras

In order to construct the Drinfeld quantum double for monoidal Hom-Hopf T-coalgebras and study the definition of quasitriangular monoidal Hom-Hopf group-algebra.The following definitions are necessary.

Definition 3.1The Duality C?.Let C=({Cα,ξCα,Δ,ε})be a G-coalgebra and A an algebra with multiplication m and unit element 1A.For any f∈Homk(Cα,A)and g∈Homk(Cβ,A),we have their convolution product by

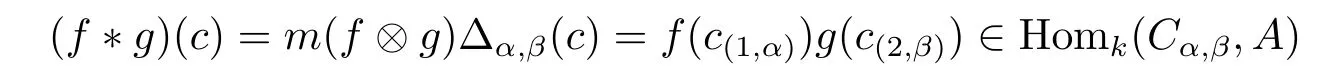
for all c∈Cα,β.Equations(2.1)and(2.2)will imply that k-space

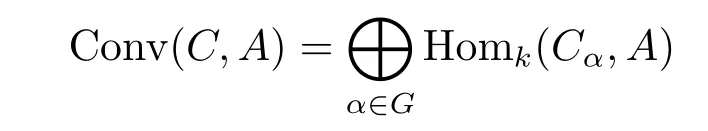
endowed with the convolution product?and the unit element 1Aε,is a G-algebra,called a convolution algebra.

In particular,for A=k,the G-algebra Conv(C,k)=is called dual to C and is denoted by C?.

Definition 3.2The MirrorLet H be a monoidal Hom-T-coalgebra.Then the notion of the mirrorof H is given by the following data.

?For any α,β∈G,the G-coalgebra structure is defined by

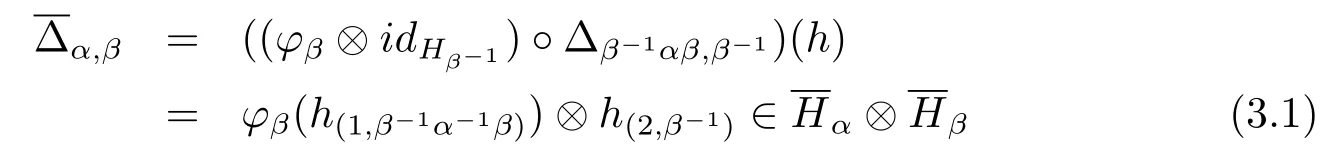
?For any α∈G,the αth component of the antipode

?For any α∈G,the αth component of the crossed map

Dually,a monoidal Hom-G-algebra is a family of k-spaces A={(Aα,ξAα)}α∈Gtogether with a family of k-linear maps m={mα,β:Aα?Aβ→Aαβ}α,β∈Gand a k-linear map η:k→A1,such that m is associative in the sense that,for any α,β,γ∈G,

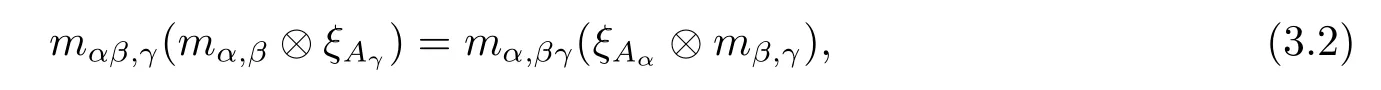
and for all α,β∈G,

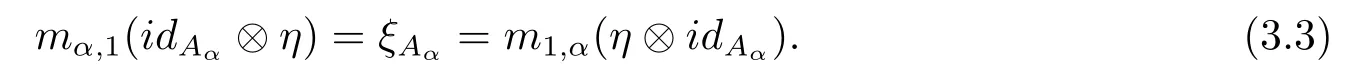
A monoidal Hom-Hopf G-algebra is a G-algebra H=({Hα,ξHα},m,η)endowed with a family of k-linear maps S={Sα:Hα→Hα-1}α∈Gsuch that each(Hα,ξHα)is a monoidal Hom-coalgebra with a comultiplication Δαand a counit εα;the map η:k→A1and the maps mα,β:Hα?Hβ→Hαβ(for all α,β∈G)are coalgebra homomorphisms;and for any α∈G,one has that

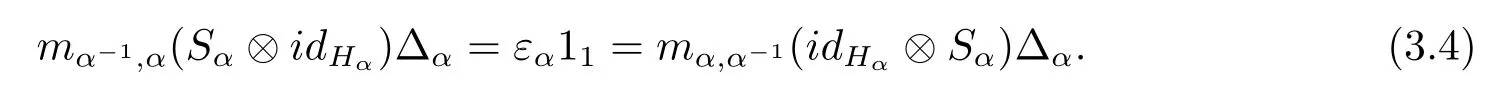
A monoidal Hom-Hopf G-algebra H is said to be of finite type if,for all α∈G,Hαis finite dimensional as k-space.

Furthermore,a monoidal Hom-Hopf T-algebra is a monoidal Hom-Hopf G-algebra H with a set of coalgebra isomorphisms ψ={ψβ:Hα→Hβαβ-1}α,β∈Gcalled a conjugation, satisfying the following conditions:

?ψ is multiplicative,i.e.,ψβ?ψγ=ψβγfor any β,γ∈G.It follows that,for any α∈G, ψ1|Hα=idHα.

?ψ is compatible with m,i.e.,for any α,β,γ∈G,we have

?ψ is compatible with η,i.e.,η?ψγ=η for any γ∈G.

Let H be a monoidal Hom-Hopf T-algebra.Similar to that of[9]we have the construction Hpk(called a packed form of H)which can form a Hom-Hopf algebra.

Remark 3.3Let H be a finite type monoidal Hom-Hopf T-algebra.The dual of H is the monoidal Hom-Hopf T-algebra defined as follows.For any α∈G,the αth component of H?is the dual coalgebraof the algebra(Hα,ξα).The multiplication of H?is given by

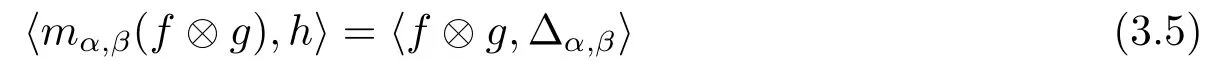
Remark 3.4Given any crossed monoidal Hom-Hopf T-coalgebra,then((H?)pk)copis the monoidal Hom-Hopf algebra obtained from(H?)pkby replacing its comultiplication with the new one Δ?=Δ?t,copgiven by

Let H be a finite type monoidal Hom-Hopf T-coalgebra.We define the Drinfeld quantum double D(T)of H as follows.Consider the following vector spaces

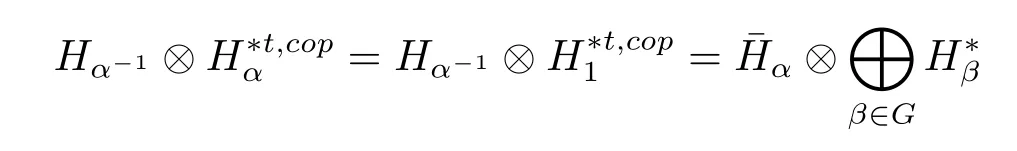
for any α∈G.A multiplication is obtained by setting,for any h,k∈Hα-1,f∈with γ,δ∈G,

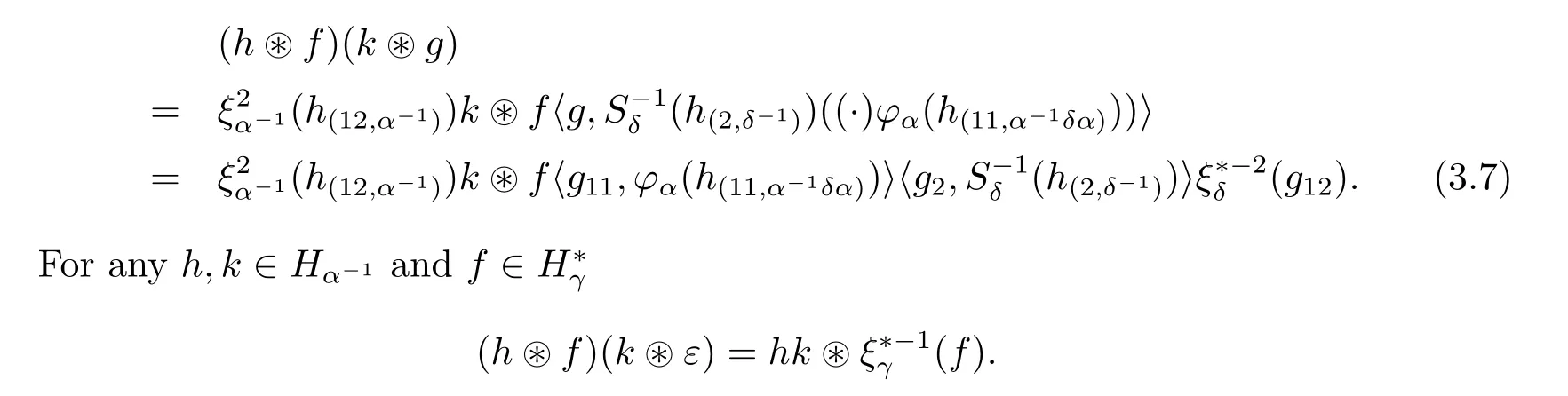
We now have the following main result of this section.

Theorem 3.5Let H be a finite-type monoidal Hom-Hopf T-coalgebra.Then D(H) is a crossed monoidal Hom-Hopf T-coalgebra with the following structures:

?For any α∈G,αth component Dα(H)is an associative algebra with the multiplication given in eq.(3.7)and with unit 1α-1ε;

?The comultiplication is given by

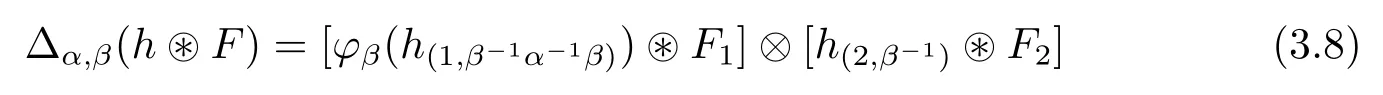
?The counit is obtained by setting

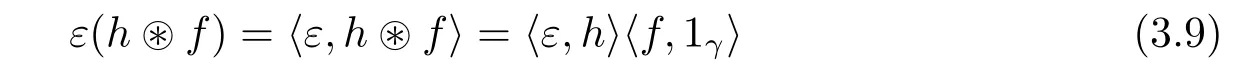
for any h∈H1and f∈with γ∈G;

?For any α∈G,the αth component of the antipode of D(H)is given by

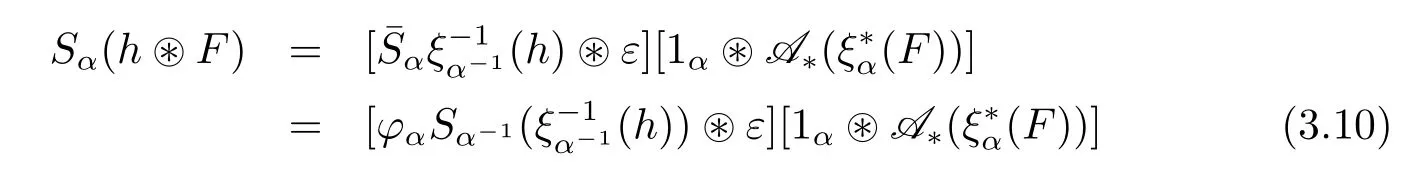
?For any α∈G,the conjugation isomorphism is given by

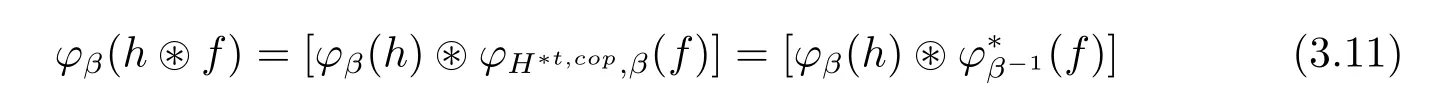
ProofFirst,for any α∈G,we will show that Dα(H)is an Hom-associative algebra with unit.Then we will show that Δ,defined as above,is multipilcative,i.e.,that any Δα,βis an algebra map.After that,we show that ε is an algebra map.Finally,we will check axioms for the antipode and the conjugation isomorphisms are compatible with the multiplication.

Hom-associativityLet α be in G.The multiplication definition eq.(3.7)is associative if and only if,for any h,k,l∈with β,δ,γ∈G,

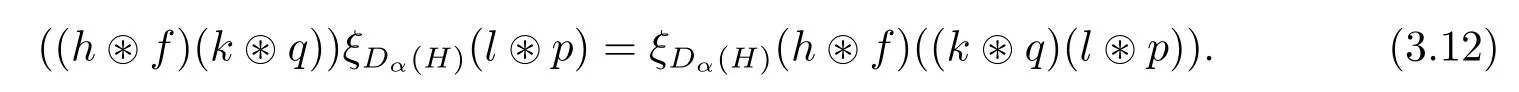
By computing the left-hand side of(3.12),we obtain

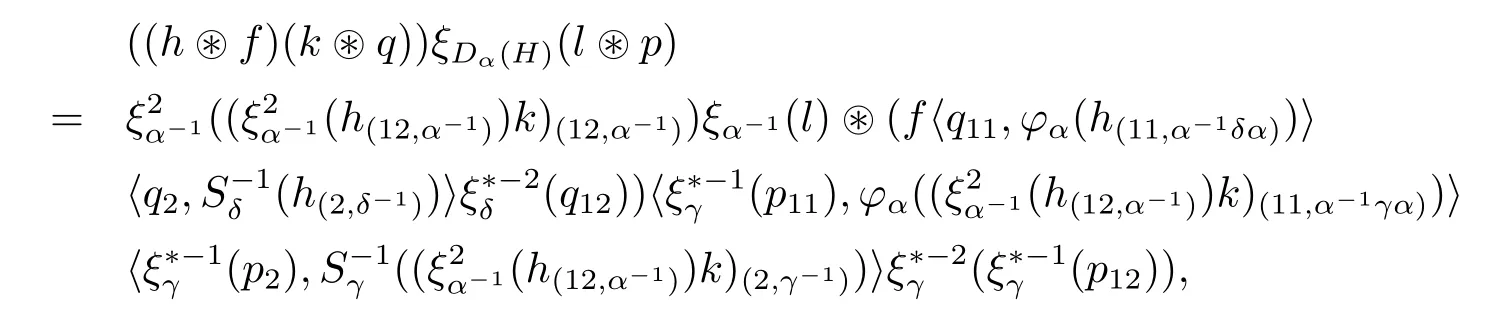
by the antimultiplicativity of S and the multiplicativity of φ,

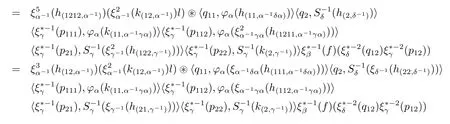
while,by computing the right-hand side,we obtain

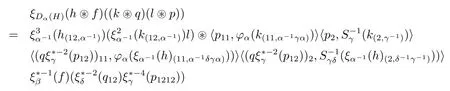
by the antimultiplicativity of S and the comultiplicativity of φ,

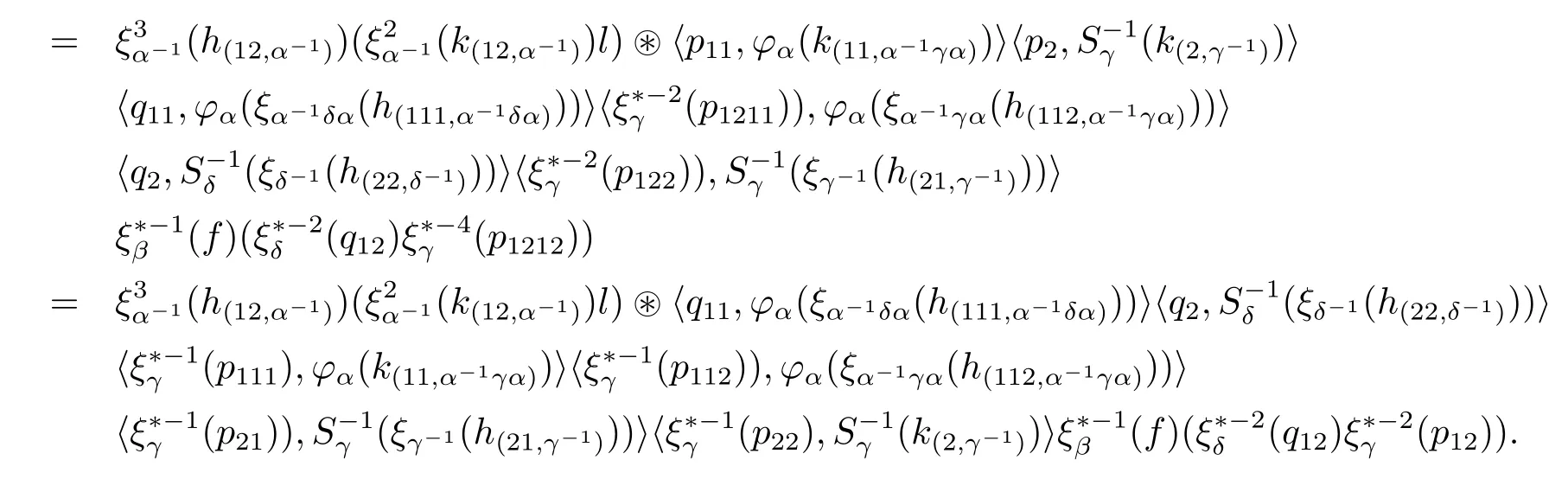
UnitLet α be in G.For any h∈Hα-1and f∈with γ∈G,we have

Remark 3.6Where we use the fact that both S1and φαcommute with ε.

Multiplicativity ofΔLet us prove that Δα,βis an algebra map for any α,β∈G. For any h,k∈Hβ-1α-1,f∈with γ,δ∈G,we have

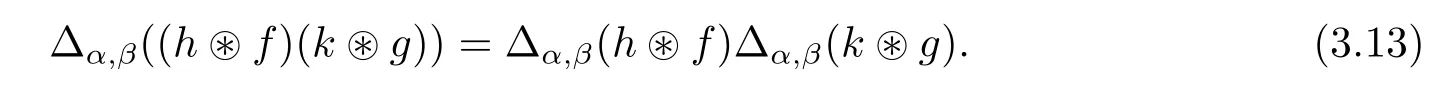
This is proved by evaluating both terms in the above equation(3.13)against the general term p?x?q?y

Multiplicativity ofε Let us prove that ε is an algebra map for any h,k∈H1,f∈and g∈with γ,δ∈G,

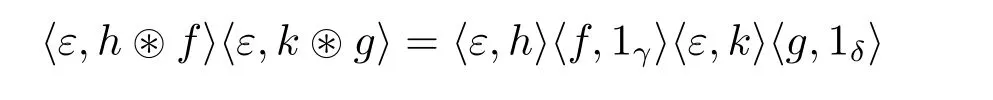
and

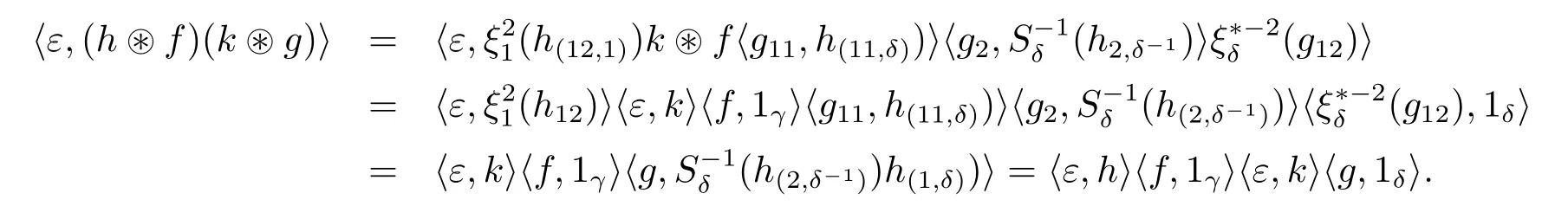
This proves that ε is multiplicative.Moreover,since ε is obviously unitary,it is an algebra homomorphism.

AntipodeLet h∈H1and let f∈with γ∈G,

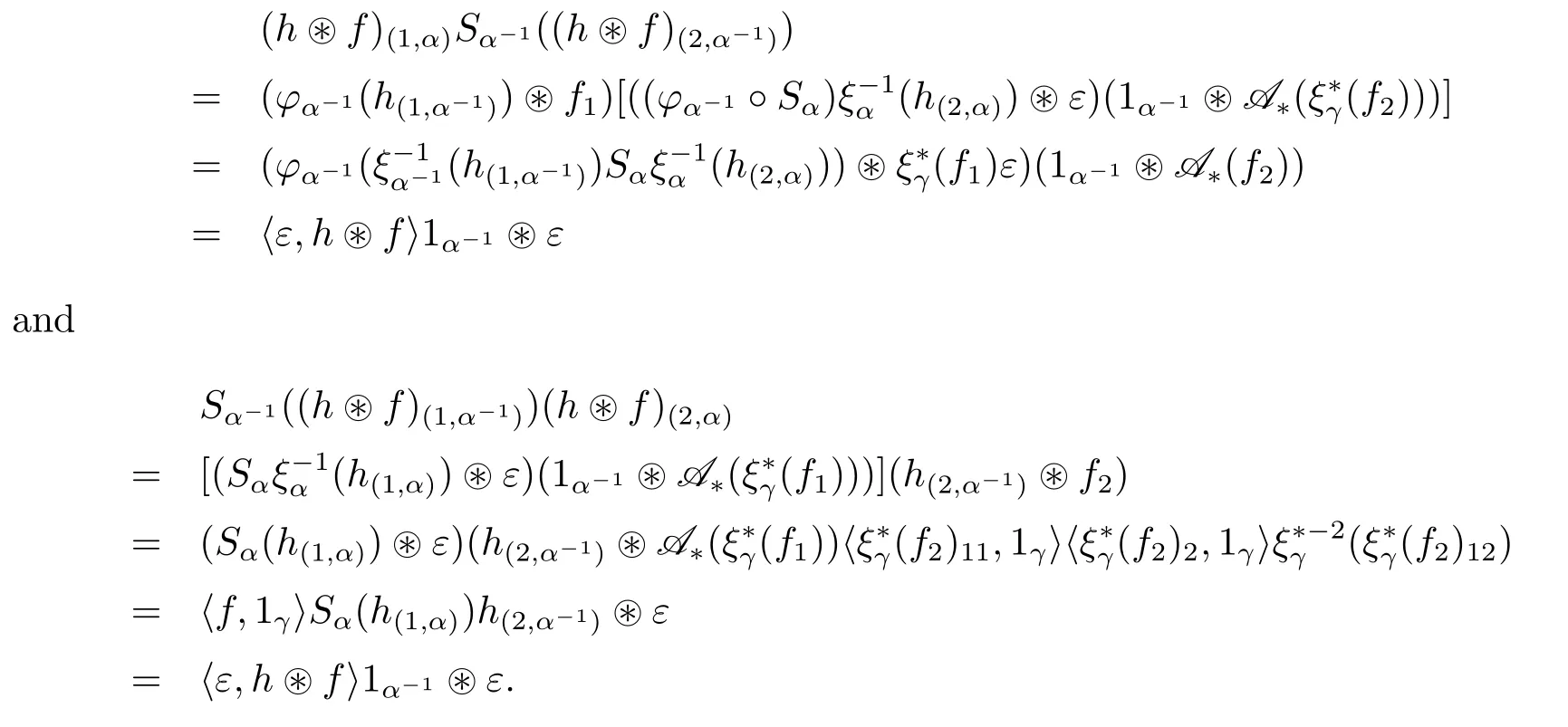
ConjugationLet us check that φβis an algebra isomorphism for any α,β∈G.For all h,k∈with γ,δ∈G,

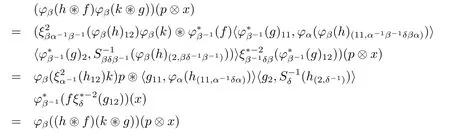
For any α∈G,we set nα=dimHα.Let(κ(α,i))i=1,···,nαand(κ(α,i))i=1,···,nαbe dual bases in Hαand.Then we have the following proposition.

Definition 3.7A quasitriangular Hom-Hopf T-coalgebra is a Hom-Hopf T-coalgebra endowed with a family R={Rα,β=κα,i?κβ,i∈Hα?Hβ}α,β∈G,called a universal R-matrix, such that Rα,βis invertible for any α,β∈G and the following conditions are satisfied:

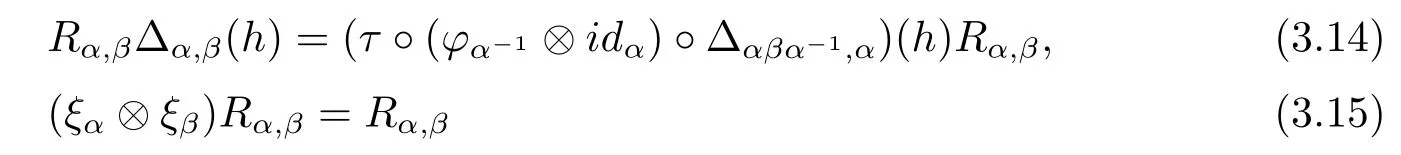
for all h∈Hαβand α,β∈G,

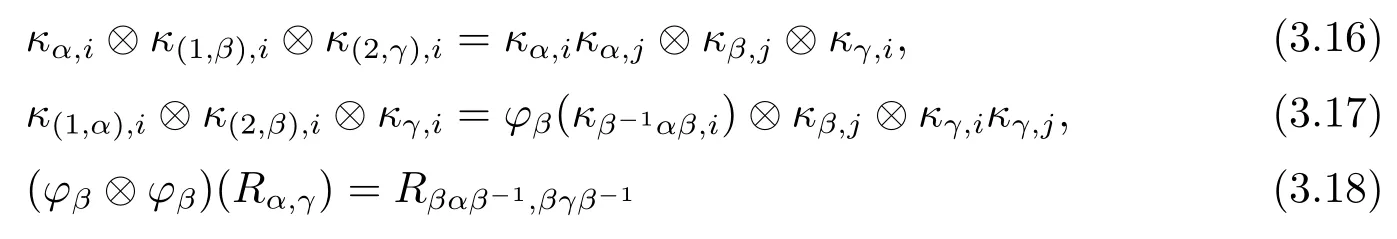
for all α,β,γ∈G.

Remark 3.8(1)We introduce the notation

(2)R1,1is an R-matrix for the Hom-Hopf algebra H1(see[8]).

Proposition 3.9The Drinfeld double D(H)={Dα(H)}α∈Ghas a quasitriangular structure given by

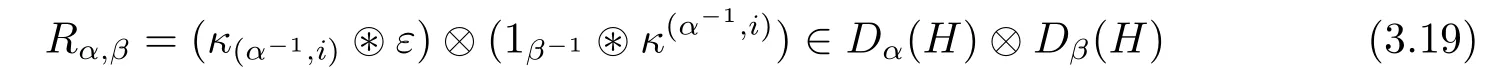
and

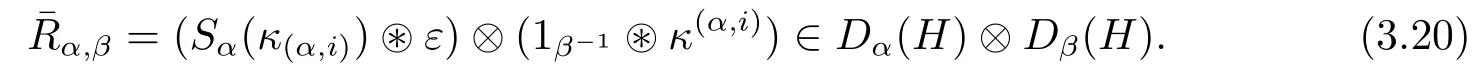
ProofRelation(3.14):

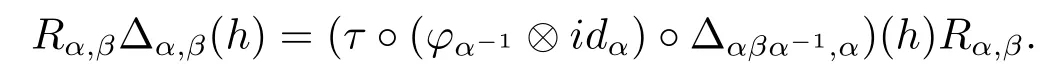
Let α,β,γ∈G.Given h∈Hβ-1α-1and f∈we have

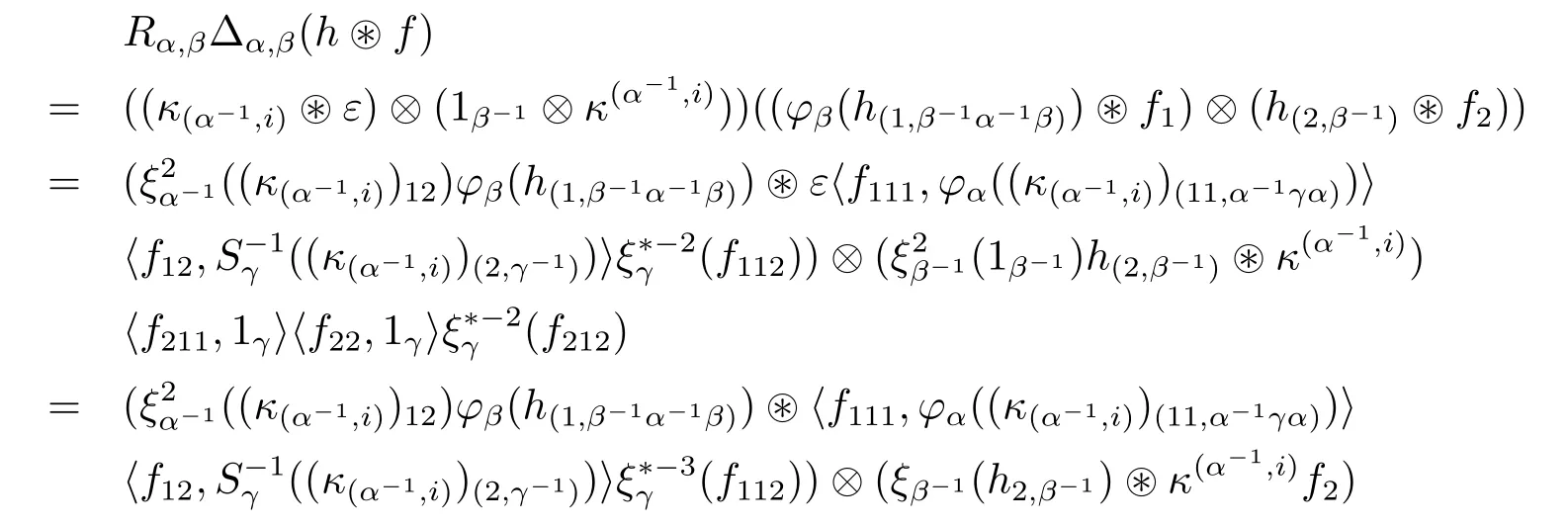
and

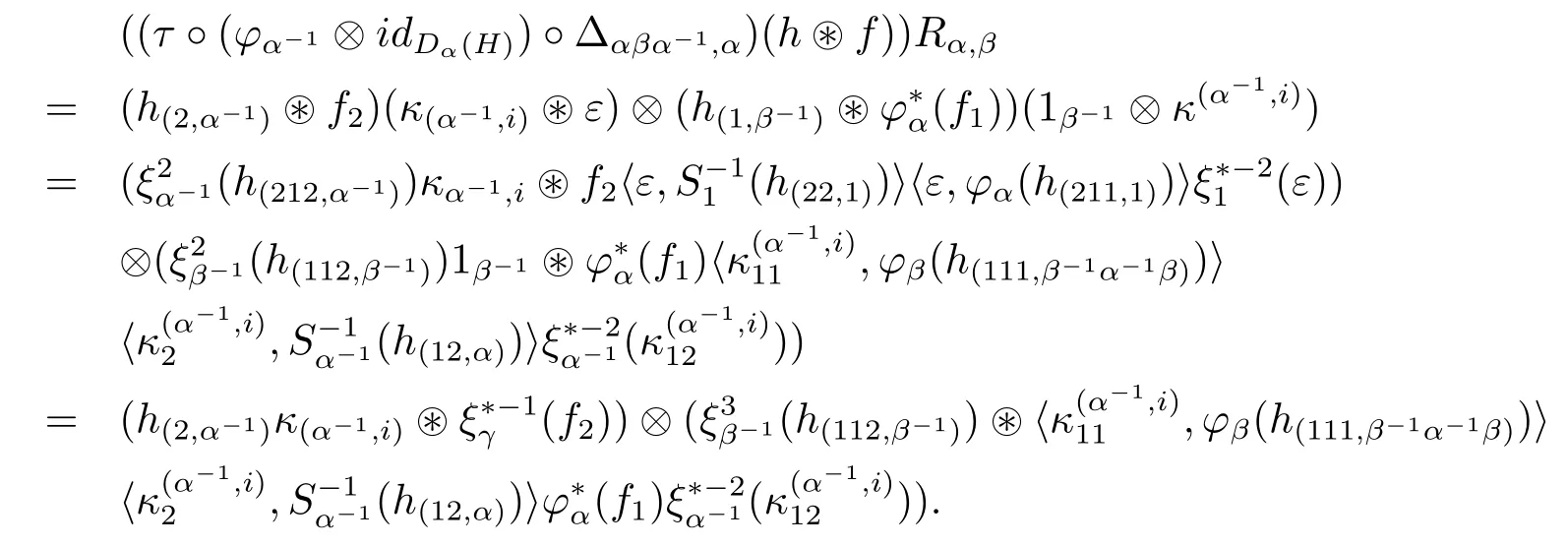
Relation(3.14)is proved by observing that evaluating the two expressions above against the tensor idα-1??idβ-1?〈·,x〉(for x∈Hα-1γ),we get the same result

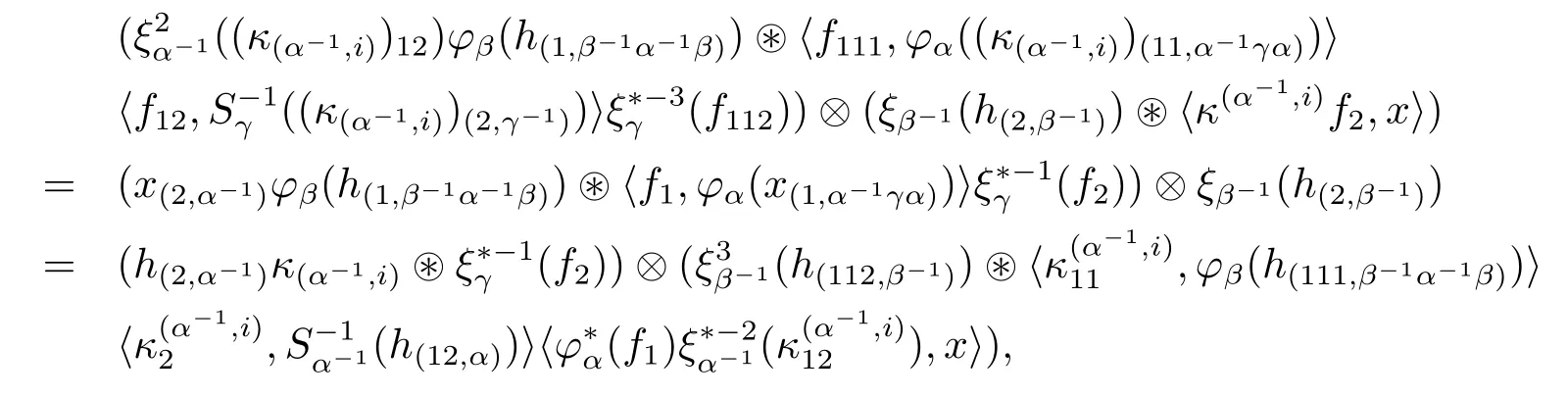
where we used

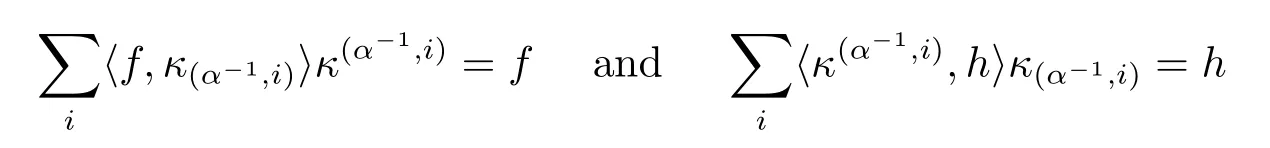
Then we check Relation(3.16)and(3.17).The identities

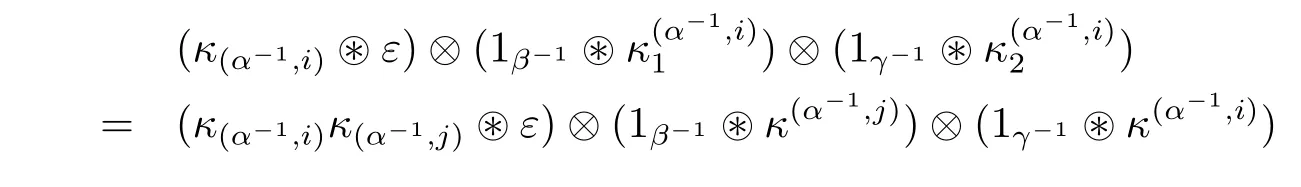
and

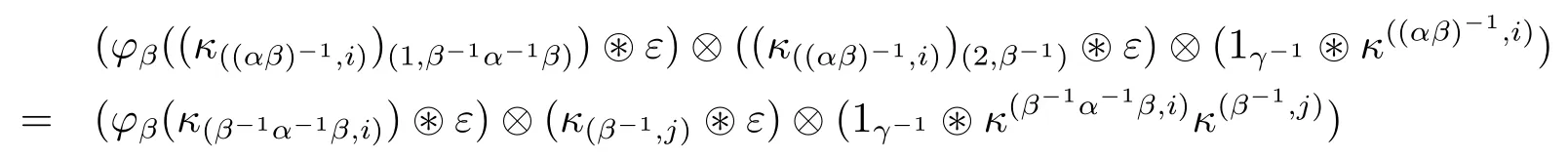
can be written as(identifying

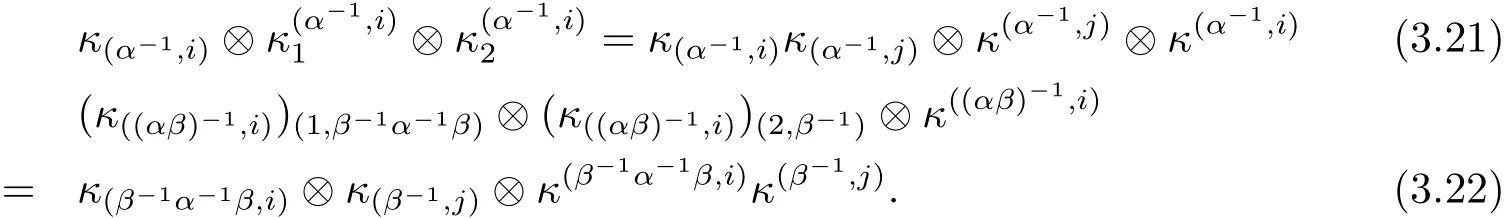
The above equalities can be verified by evaluating both sides on element f∈in the first factor(respectively,on h∈in the third factor)(see Zunino[9],Theorem 11).

Finally,let us check that

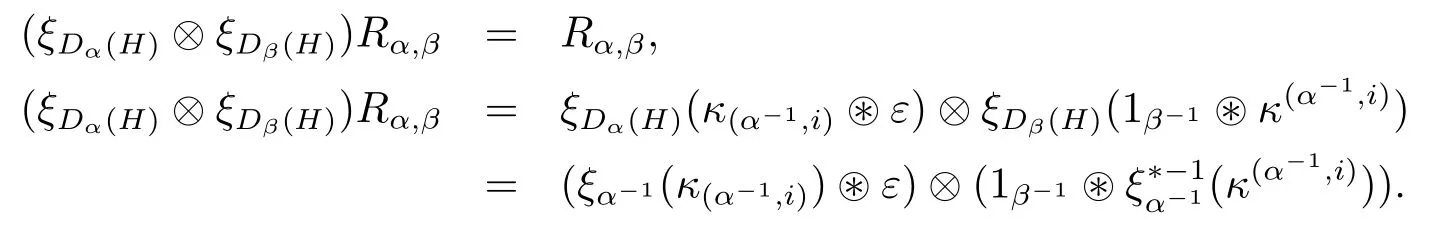
Now,ξα-1is a linear isomorphism,so(ξα-1(κ(α-1,i)))i=1,···,nαis a basis of Hα-1,and

is its dual basis.So(ξDα(H)?ξDβ(H))Rα,β=Rα,β,

for x∈Hα-1.

This completes the proof.

[1]Turaev V,Homotopy field theory in dimension 3 and crossed group-categories[GT].http:// arxiv.org/abs/math/0005291.

[2]Freyd P,Yetter D,Braided compact closed categories with applications to low-dimensional topology[J].Adv.Math.,1989,77(2):156–182.

[3]Zhou Xuan,Yang Tao,Kegel’s theorem over weak Hopf group coalgebras[J].J.Math.,2013,33(2): 228–236.

[4]Yang Tao,Another construction of the braided T-category[RA].http://arxiv.org/abs/1409.6936.

[5]Caenepeel S,Goyvaerts I,Monoidal Hom-Hopf algebras[J].Commun.Alg.,2011,39:2216–2240.

[6]Virelizier A.Hopf group-coalgebra[J].J.Pure Appl.Alg.,2002,171:75–122.

[7]Drinfeld V.Quantum groups[A].Proceedings of the international congress of mathematicians[C]. (Berkeley,CA),Vol.1,Providence,RI:Amer.Math.Soc.,1987:789–820.

[8]Chen Yuanyuan,Wang Zhongwei,Zhang Liangyun.Quasitriangular Hom-Hopf algebra[J].Colloq. Math.,2014,137(1):67–88.

[9]Zunino M,Double construction for crossed Hopf coalgebra[J].J.Algebra.,2004,278:43–75.

Monoidal Hom-Hopf群-余代數(shù)上的Drinfeld量子偶

游彌漫1,周楠2

(1.華北水利水電大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,河南鄭州450046)

(2.東南大學(xué)數(shù)學(xué)系,江蘇南京211189)

本文研究了monoidal Hom-Hopf群-余代數(shù)上的Drinfeld量子偶的問題.利用交叉monoidal Hom-Hopf T-余代數(shù)的定義及擬三角monoidal Hom-Hopf群-余代數(shù)的定義,獲得了此Drinfeld量子偶是擬三角monoidal Hom-Hopf群-余代數(shù)的結(jié)果.

擬三角;Monoidal Hom-Hopf群-余代數(shù);Drinfeld量子偶

O153.3

tion:16T05;16T15

A

0255-7797(2017)01-0063-11

?Received date:2014-12-23Accepted date:2015-07-06

Foundation item:Supported by the NSF of China(11371088;11601078);the NSF of Jiangsu Province(BK2012736);the NSF of Jiangsu Province(KYLX15-0103).

Biography:You Miman(1984–),female,born at Zhoukou,Henan,lecturer,major in Hopf Algebra and locally compact quantum group.

Zhou Nan.