LIU Xiao,YU Hong-wei

(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China )

OPTIMAL DIVIDEND STRATEGY IN THE BROWNIAN MOTION MODEL WITH INTEREST AND RANDOMIZED OBSERVATION TIME

LIU Xiao,YU Hong-wei

(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China )

In this paper we study the optimal dividend problems in the Brownian motion model with interest and randomized observation time.By using stochastic control theory,we obtain the associated Hamilton-Jacobi-Bellman(HJB)equation with the optimal value function,which show that the optimal dividend strategy is a barrier strategy,and give the explicit expression for the optimal value function,which generalize the results of[19].

dividend;ruin;HJB equation

1 Introduction

Finding the optimal dividend strategy for an insurance company is a very popular research topics in actuarial mathematics.It was first proposed for measuring the stability of an insurance company by De Finetti[1].In recent years,many papers were published about the optimal dividend strategy.See,for example,Jeanblanc and Shiryaev[2],Amussen et al.[3],Gerber and Shiu[4],Bai and Paulsen[5],Bayraktar et al.[6,7],Wang[8] and the references therein.One can refer to Avanzi[9]and Albrecher and Thonhauser [10]for knowing more about the models with dividends before 2009.But in all of the above-mentioned literatures,the surplus process need continuously observed,which cannot be realized in practice.Albrecher et al.[11–14]first introduced the idea of randomized observation time in the classical risk model,the diffusion model and the Lvy model,in which the risk process can be“l(fā)ooked”only at random times.Avanzi[15]and Peng et al. [16]considered this idea in the dual model.The model was extended to the dual model with diffusion by Liu et al.[17]and Avanzi et al.[18].

Brownian motion model is a Brownian motion with a positive drift.This model can be viewed as a diffusion approximation of the classical risk model,but it often leads to more simple calculation of the characteristics than the classical risk model,such as ruin probability.Wang and Liu[19]studied the expected discounted sum of dividends paid until ruin in the Brownian motion model with interest under the assumption that the dividend strategy is restricted to a barrier strategy and the dividends can only be paid at some randomized observation times.Naturally,one interesting problem appears:is the barrier strategy optimal or not?In this paper,assuming that the surplus of a company is modeled by the Brownian motion model with interest,we show that the barrier strategy is the optimal dividend strategy among all the admissible dividend strategies by using stochastic control theory.

This paper is organized as follows.In Section 2,the Brownian motion model with interest and randomized observation time is shortly discussed.In Section 3,it is shown that the optimal value function can be characterized by the associated HJB equation.In addition,the verification theorem is stated and proved.In Section 4,we show that the optimal dividend strategy is a barrier strategy,and the explicit expression for the optimal value function is given.

2 The Model

Let(?,F,{Ft}t≥0,P)be a filtered probability space on which all random processes and variables introduced in the following are defined.We assume that the surplus process of an insurance company is modeled by the Brownian motion model and the company invests all the surplus in the risk-free asset.Let{X(t);t≥0}be the surplus of the company before a dividend strategy is imposed.Then{X(t);t≥0}satisfies the following stochastic differential equation

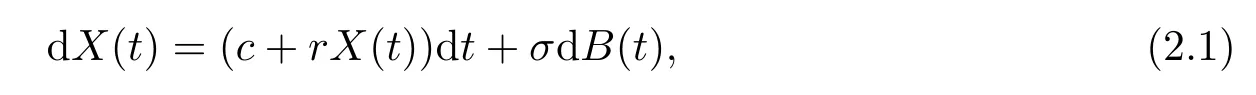
where c＞0 is the drift coefficient,r＞0 is the force of interest,σ＞0 is the standard deviation and{B(t);t≥0}is a standard Brownian motion.

Let{Ti;i=1,2,···}denote the random observation times.Let Zi=Ti-Ti-1with T0=0 be the ith time interval between observations,we assume that{Zi;i=1,2,···}are independent random variables with an exponential distribution of meanLet Libe the dividend payment at Ti.Let{XL(t);t≥0}denote the surplus process after an admissible dividend strategy L is imposed.

A dividend strategy L={Li;i=1,2,···}is called admissible,if Li≤XL(Ti-)and no dividend is paid after ruin.Denote Π the set of all admissible dividend strategies.

Let τL=inf{t:XL(t)≤0}be the ruin time.Assume that dividends are discounted at a constant force of interest δ.In this paper we assume δ＞r.For a given admissiblestrategy L,we define the value function VLas

where I{·}is the indicator function and Exis the expectation corresponding to the law of {XL(t);t≥0}with XL(0)=x.We aim to find the optimal value function,which is defined as

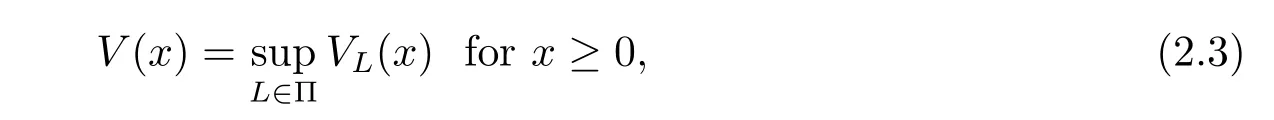
and find an optimal dividend strategy L?that satisfies V(x)=VL?(x).For technical reasons, we define V(x)=0 for x＜0.

3 Hamilton-Jacobi-Bellman Equation

In this section,the HJB equation associated with(2.3)is obtained and the verification theorem is stated and proved.

Suppose V(x)is twice continuously differentiable on[0,∞).Consider a small time interval(0,△t],where△t＞0 is sufficiently small so that the surplus process will not reach 0 if there is no dividend paying in the interval.The strategy L is that paying amount l≥0 as dividend if T1≤△t.By the strong Markov property of the surplus process,we have

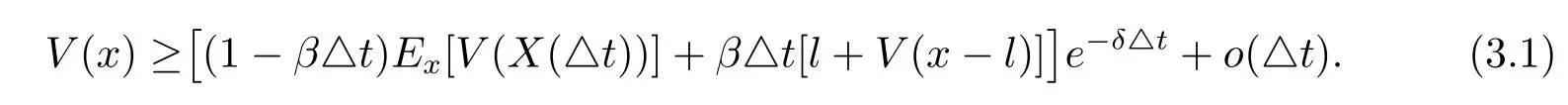
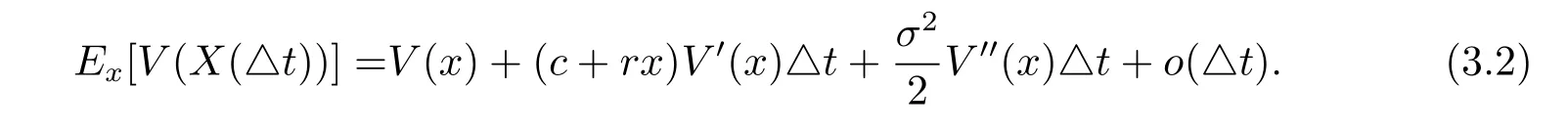
Plugging(3.2)into(3.1),rearranging the terms,dividing by△t and then letting△t tend to 0,we have

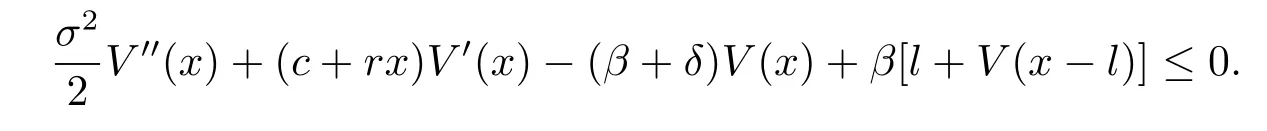
We obtain the HJB equation associated with(2.3)as follows

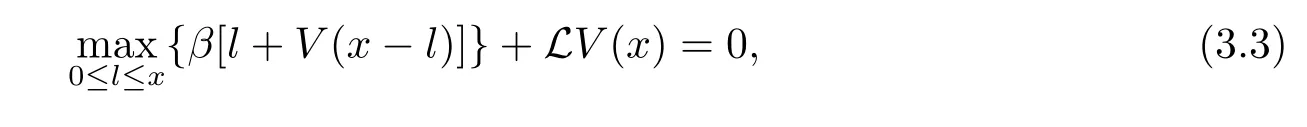
where

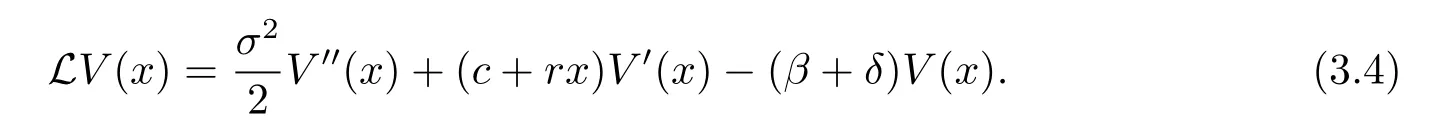
Because ruin is immediate and no dividend is paid if the initial surplus x=0,we get the boundary condition V(0)=0.

The next Theorem states the verification theorem.

Theorem 3.1Let H(x):[0,∞)→[0,∞)with H(0)=0 be a twice continuously differentiable function.Assume that H(x)is dominated by a linear function.If H(x) satisfies

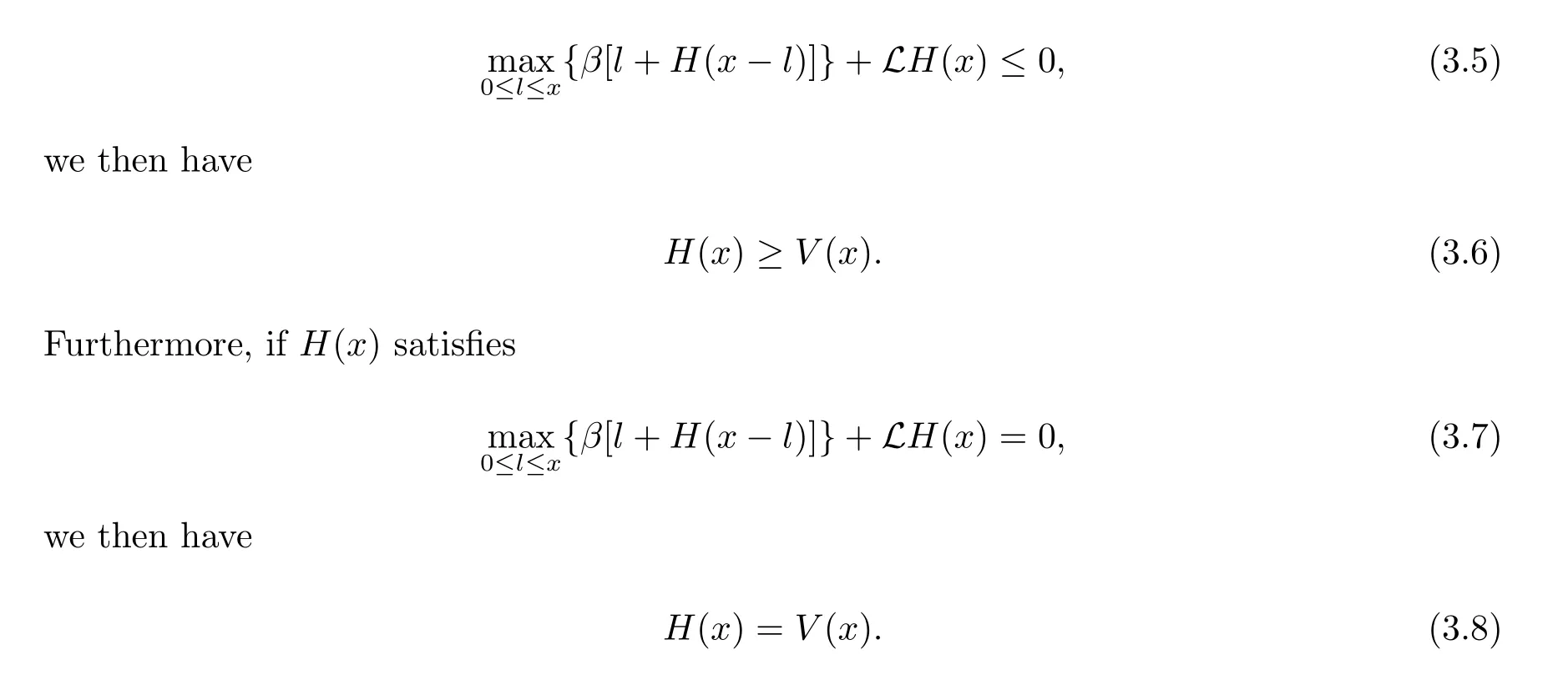
ProofLet L={Li;i=1,2,···}be any admissible strategy and XL(t)be the surplus process associated with the dividend strategy L.Denote S={Ti;i=1,2,···}. For convenience we let H(x)=0 for x＜0.From generalized Itformula,we know that

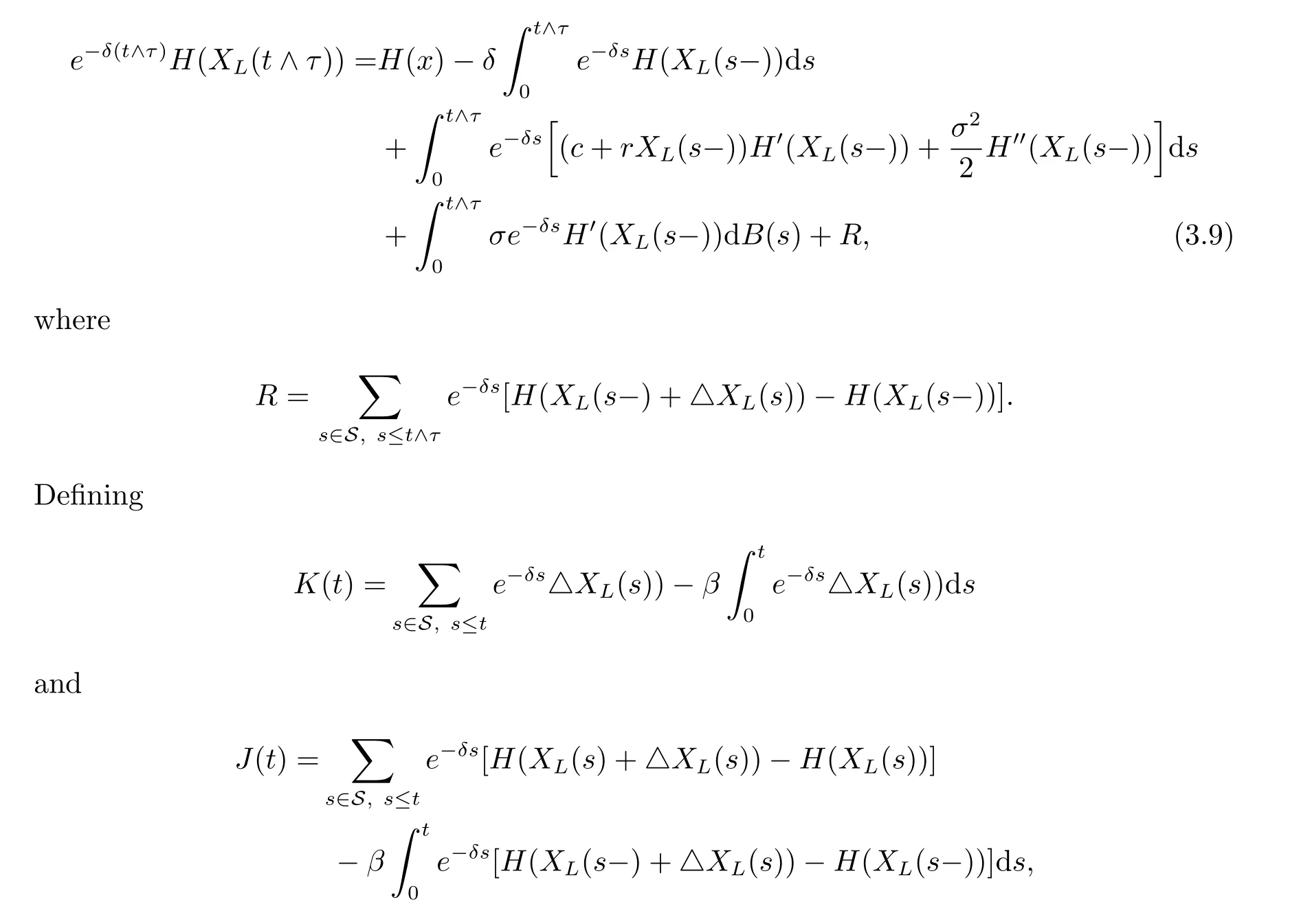
we have

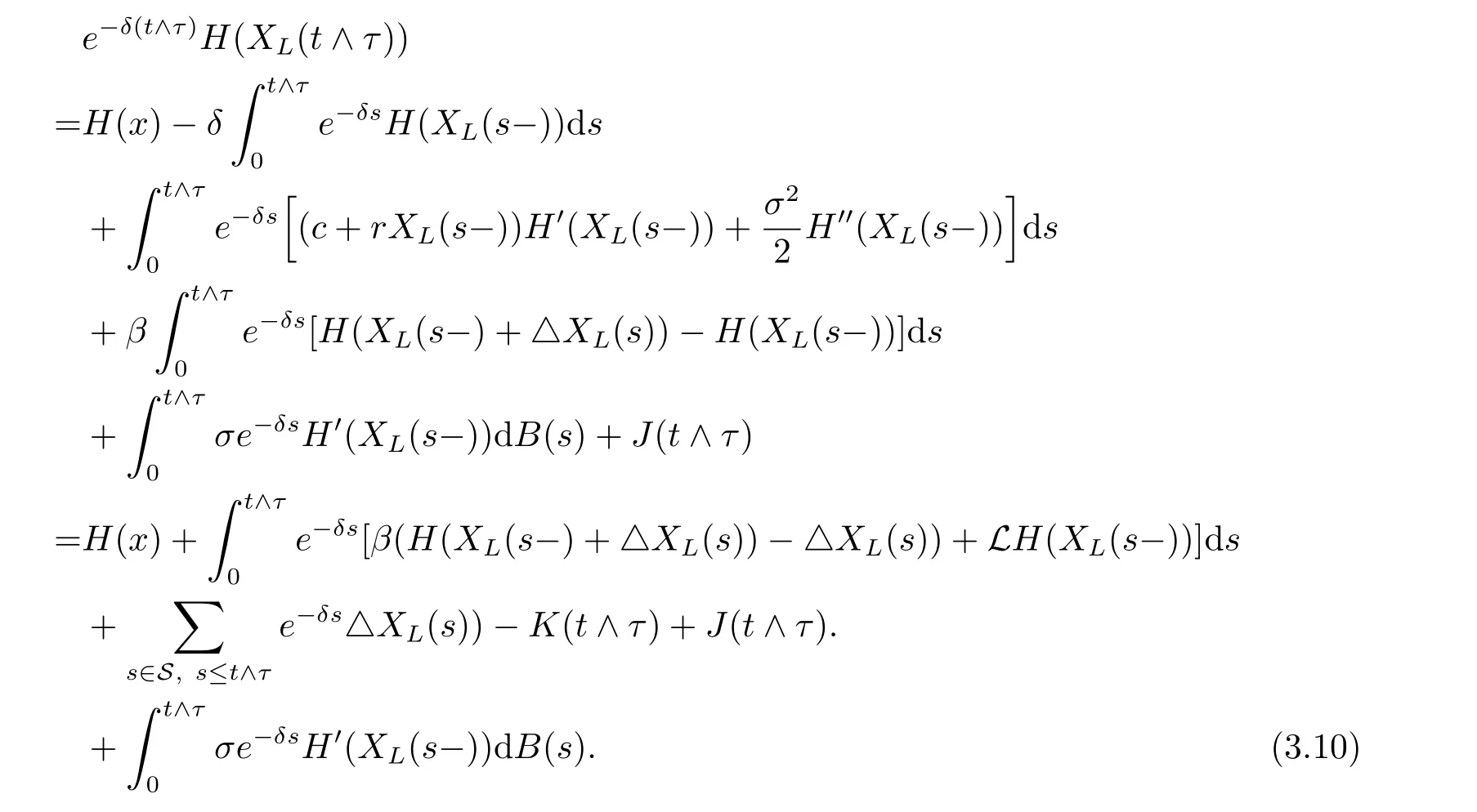
Noting that K(t)and J(t)can be denoted as

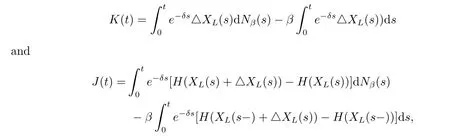
where Nβ(t)is a Poisson process with parameter β,we then have that K(t)and J(t)are martingales with zero-expectation,together with condition(3.5),we get

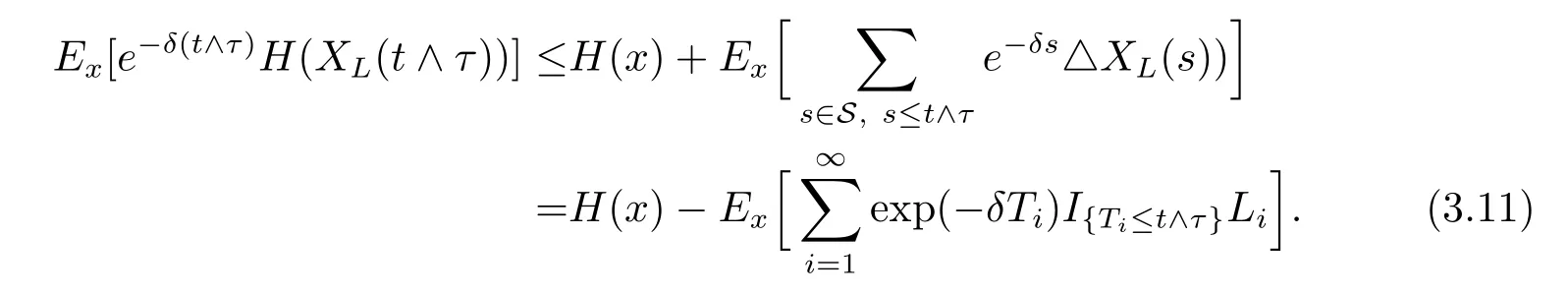
Because H(x)is dominated by a linear function,we know that

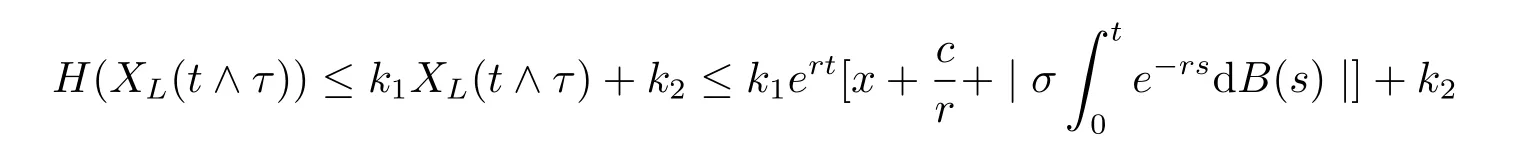
for some positive constants k1and k2,hence

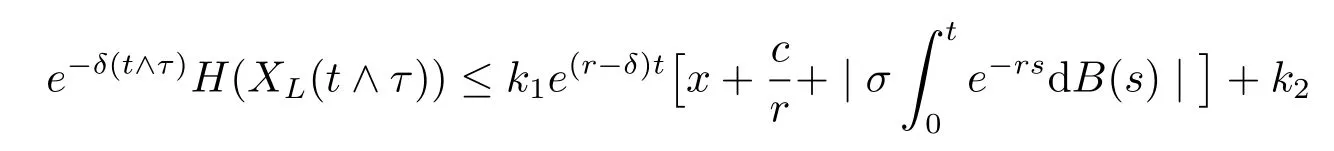
if t≤τ and e-δ(t∧τ)H(XL(t∧τ))=0 if t＞τ.By dominated convergence theorem,we have

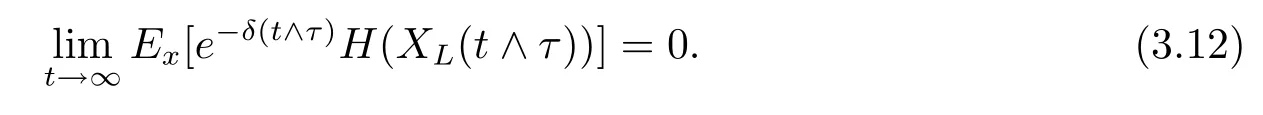
Let t tend to∞in(3.11)and using(3.12)yield

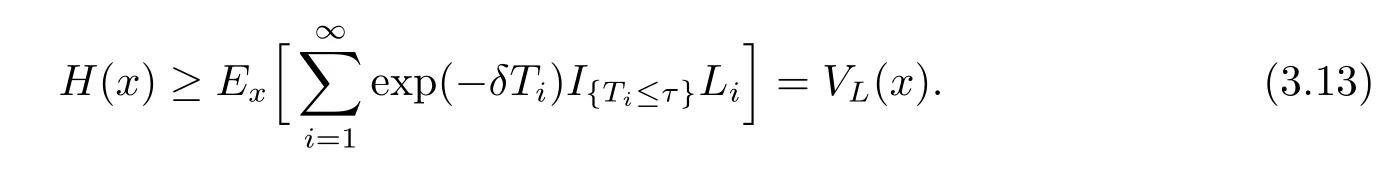
Because(3.13)holds for any admissible strategy L,we have H(x)≥V(x).

If condition(3.7)holds,we take the admissible strategysatisfies

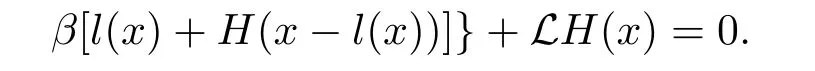
By a similar argument,we get H(x)=VL?(x),hence H(x)=V(x)and L?is the optimal dividend strategy.The proof is completed.

4 The Optimal Dividend Strategy

In this section,we show that there exists a twice continuously differentiable concave function V(x)which is dominated by a linear function and a solution to the HJB equation (3.3)with the boundary condition V(0)=0,and the optimal dividend strategy is a barrier strategy.In addition,the explicit expression for V(x)is given.

Let us find a twice continuously differentiable,increasing and concave solution V(x)to (3.3)with V(0)=0,and V(x)is dominated by a linear function.If there exists some point b＞0 with the following properties:

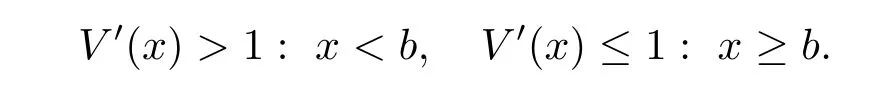
Because

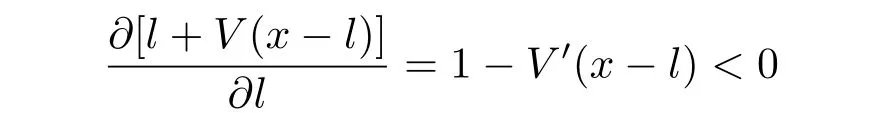
for l∈[0,x]if x＜b,and 1-V′(x-l)≥0 for l∈[0,x-b)but 1-V′(x-l)＜0 for l∈[x-b,x)if x＞b,we have that l+V(x-l)is decreasing in[0,b)with respect to l if x＜b,and l+V(x-l)is increasing in[0,x-b)but decreasing in[x-b,x]with respect to l if x＞b.Hence a candidate of the optimal dividend strategy should be

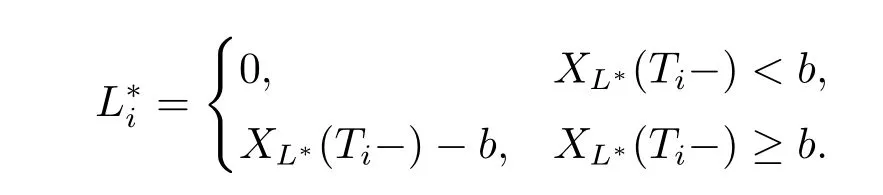
Therefore(3.3)is translated into

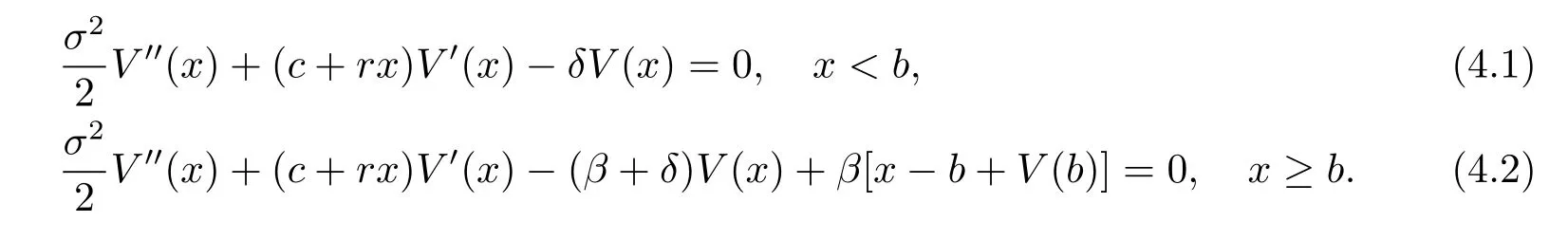
Noting that V(x)behaves differently depending on wether x is below or above the barrier b, we denote V(x)as

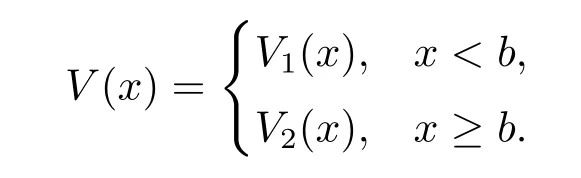
According to Theorem 16.69 of Breiman L[20],we know that equation(4.1)has two positive independent solutions f1(x)and f2(x),and thus the equation

has two positive independent solutions f3(x)and f4(x).In addition,f1(x)and f3(x)are strictly decreasing,but f2(x)and f4(x)are strictly increasing.In fact,the explicit expressions for f1(x),f2(x),f3(x)and f4(x)are given by

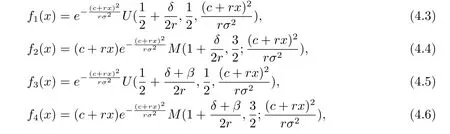
where M(a1,a2;x)and U(a1,a2;x)are called the confluent hypergeometric functions of the first and second kinds respectively.M(a1,a2;x)and U(a1,a2;x)satisfy the following properties:

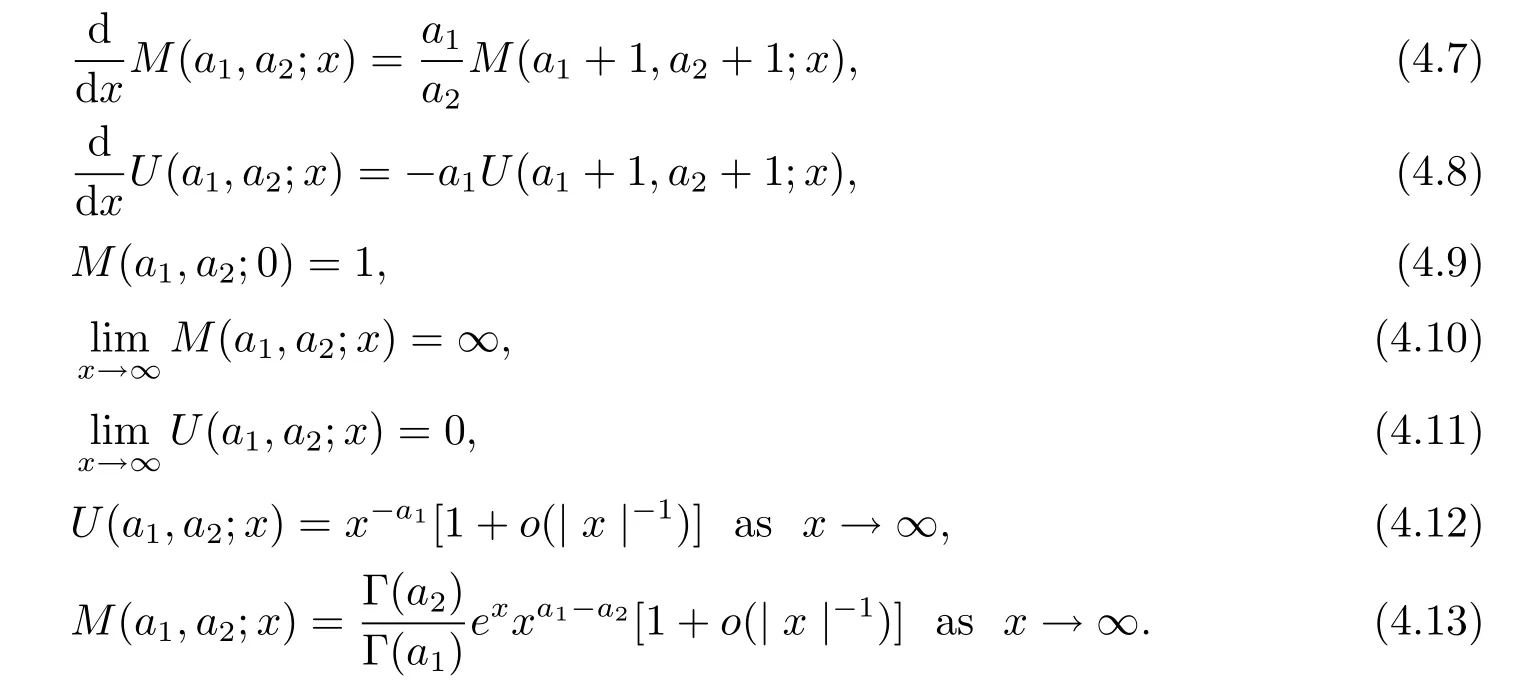
Therefore the solution of(4.1)can be expressed as

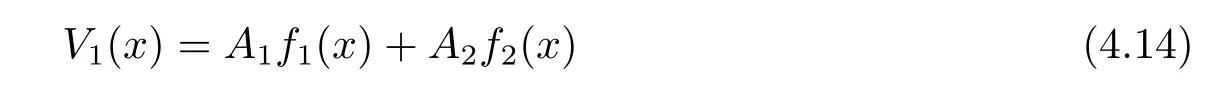
for some constants A1and A2.

for some constants A3,D and F.

Plugging(4.15)into(4.2),we get

and

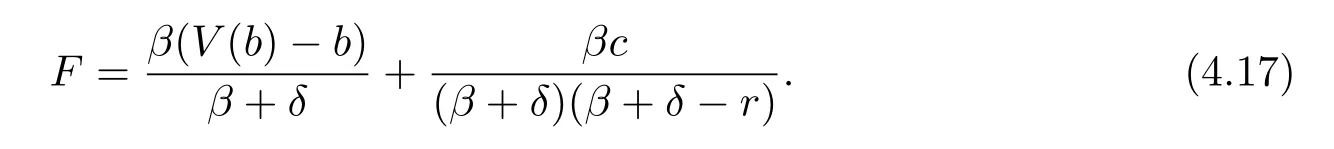
Plugging(4.16)and(4.17)into(4.15)and letting x tend to b,we have

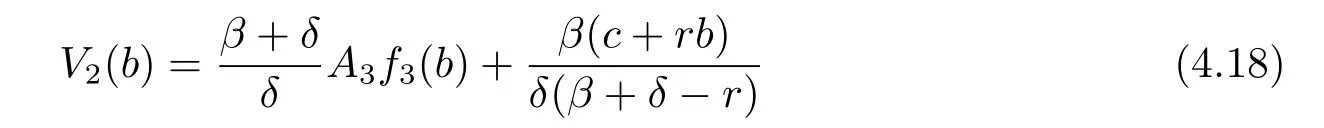
and

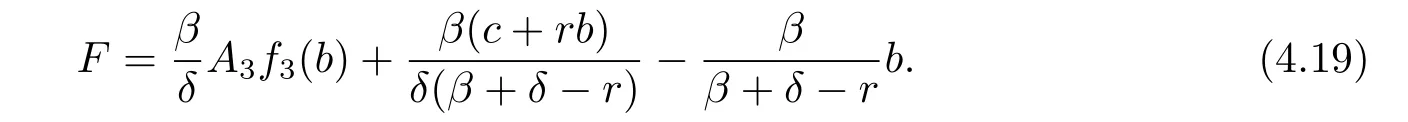
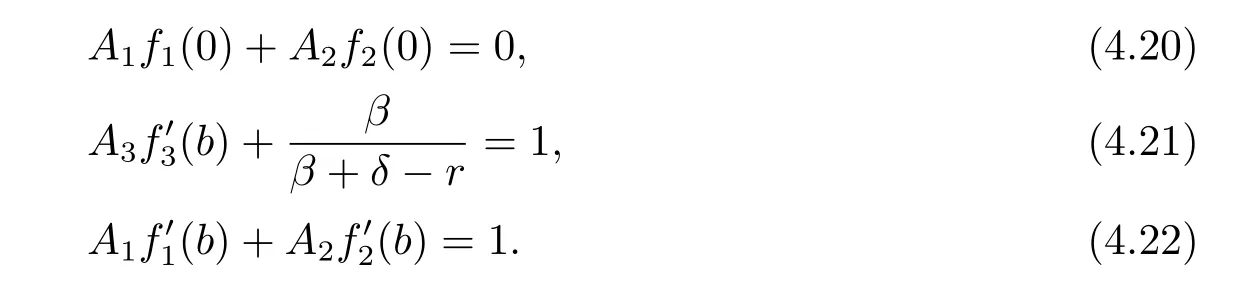
From(4.20)–(4.22),we have

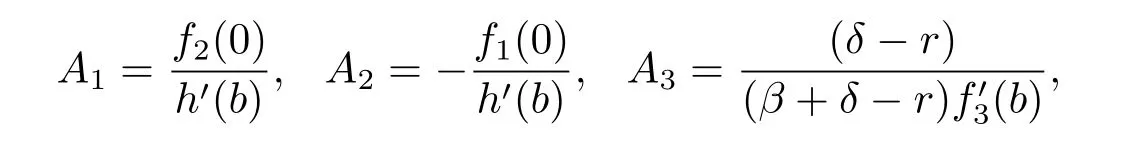
where h(x)=f1(x)f2(0)-f1(0)f2(x).The value of b is determined by V1(b-)=V2(b+), i.e.,

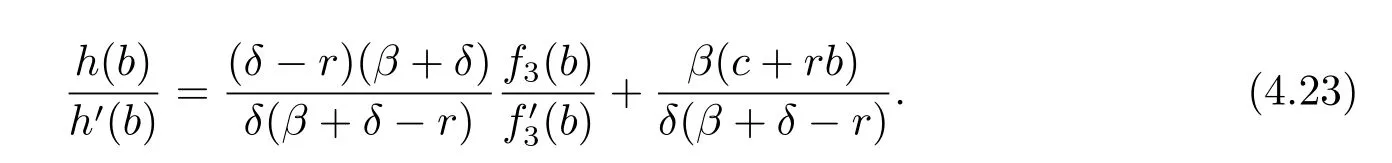
Using(4.12)and(4.13),we can easily show that

and

Hence there exists a positive solution to the equation(4.23)if

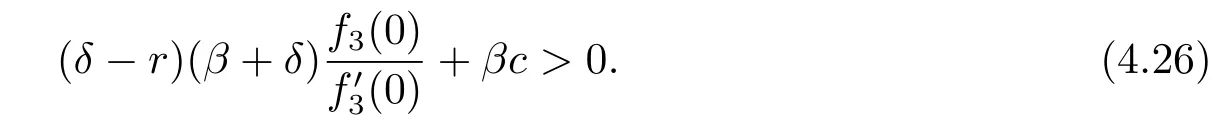
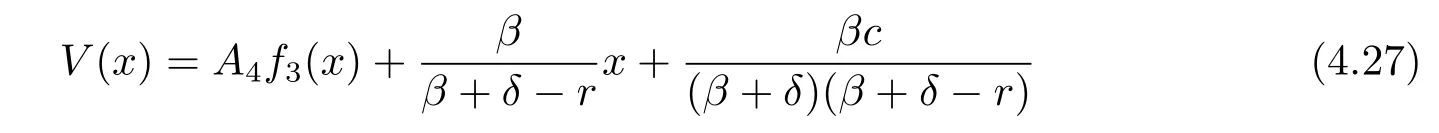
for some constant A4.The condition V(0)=0 implies that

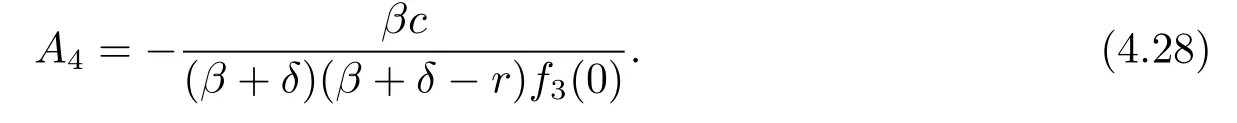
Theorem 4.1If(δ-r)(β+δ)+βc≤0,then the function

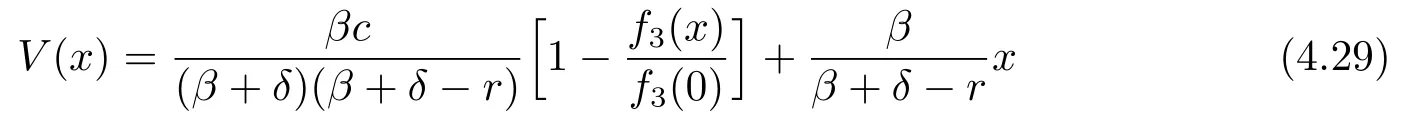
is twice continuously differentiable,concave,dominated by a linear function and a solution to the HJB equation(3.3).

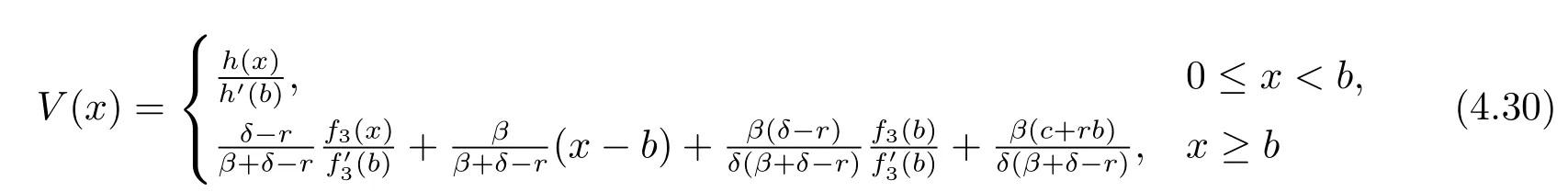
is twice continuously differentiable,concave,dominated by a linear function and a solution to the HJB equation(3.3),where b is determined by(4.23).

ProofIf(δ-r)(β+δ)+βc≤0,it is straightforward to verify that the function given by(4.29)is twice differentiable and satisfies the differential equation(4.2)with boundary condition V(0)=0.Because of the facts that

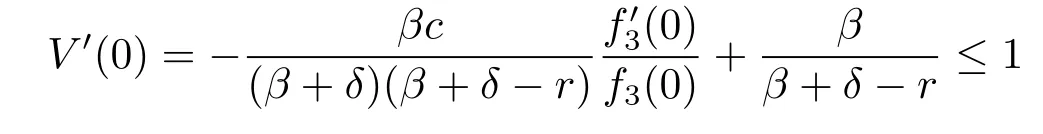
and

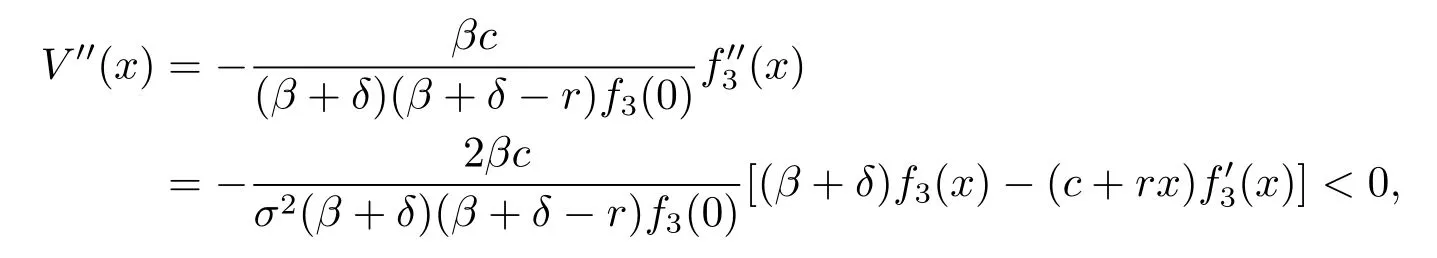
we know that V′(x)＜1 for any x＞0,hence V(x)is concave and satisfies the HJB equation (3.3)with boundary condition V(0)=0.

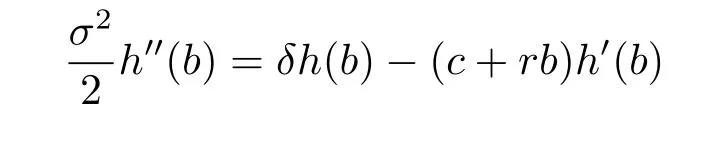
and

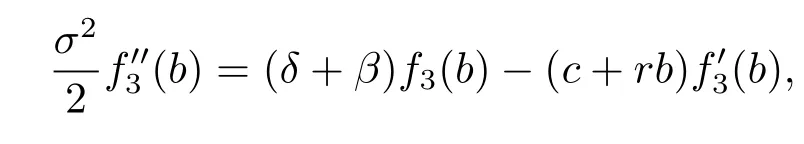
we have

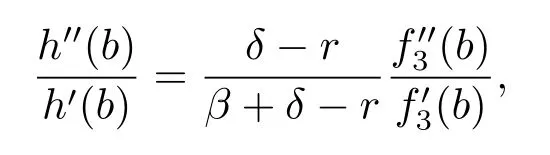
which implies that the function given by(4.30)is twice differentiable.Noticing that,for x≥b,we have

and hence V′(x)＜1.For x＜b,using the formulas

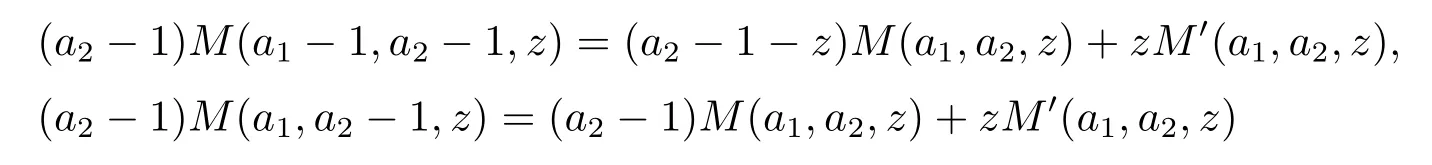
and

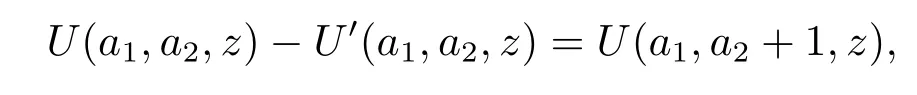
we have

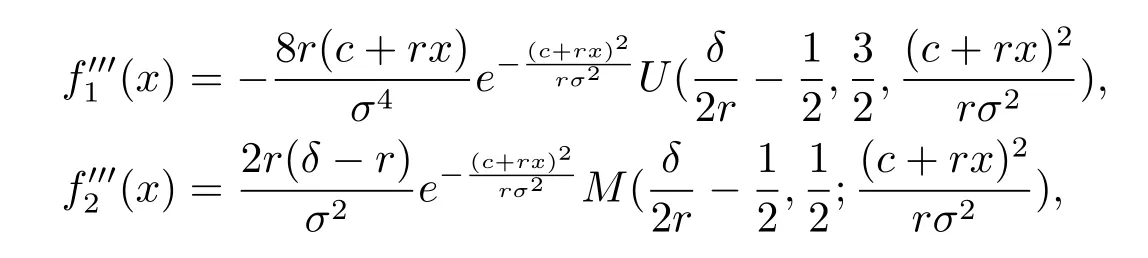
hence

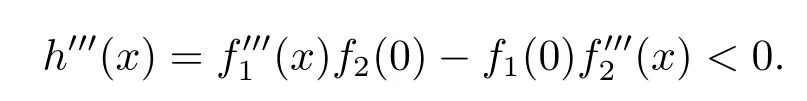
Noting that h′(b)=＜0,then it follows that V′′′(x)＞0.Hence V′′(x)is strictly increasing.Since

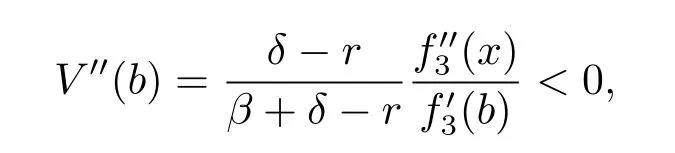
we have V′′(x)＜0 for any x＜b,therefore V′(x)is decreasing in[0,b].Because V′(b)=1, we have V′(x)＞1 for x≤b.Hence V(x)is concave and satisfies the HJB equation(3.3) with boundary condition V(0)=0.The proof is completed.

Combining Theorem 3.1 with Theorem 4.1,we obtain the following proposition.

Proposition 4.2The optimal dividend strategy is a barrier strategy.The barrier is 0 if

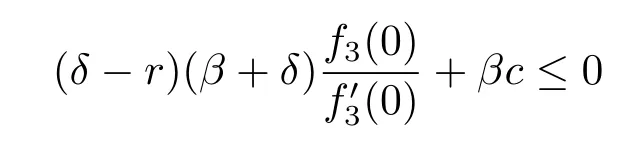
or determined by(4.23)if

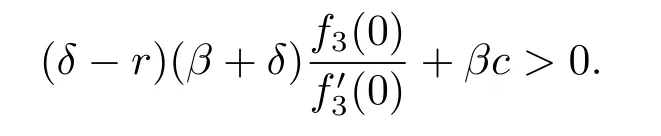
The functions V(x)given by(4.29)and(4.30)are the optimal value functions respectively.

[1]Finetti B.Su un’impostazione alternativa dell teoria collectiva del rischio[R].New York:Transaction of 15th International Congress of Actuaries,1957,2:433–443.

[2]Jeanblanc M,Shiryaev A N.Optimization of the flow of dividends[J].Russian Math.Surv.,1995, 50(2):257–277.

[3]Asmussen S,Hφgaard B,Taksar M.Optimal risk control and dividend distribution policies:Example of excess-of-loss reinsurance for an insurance corporation[J].Fin.Stoch.,2000,4(3):299–324.

[4]Gerber H U,Shiu E S W.On optimal dividends strategies in the compound Poisson model[J].North Amer.Act.J.,2006,10(2):76–93.

[5]Bai Lihua,Paulsen J.Optimal dividend policies with transaction costs for a class of diffusion processes[J].SIAM J.Contr.Optim.,2010,48(8):4987–5008.

[6]Bayraktar E,Kyprianou A,Yamazaki K.On optimal dividends in the dual model[J].Astin Bull., 2013,43(3):359–372.

[7]Bayraktar E,Kyprianou A,Yamazaki K.Optimal dividends in the dual model under transaction costs[J].Insurance:Math.Econ.,2014,54:133–143.

[8]Wang Cuilian.Dividend problems in the classical compound poisson risk model with mixed exponentially distributed claim size[J].J.Math.,2015,35(3):559–566.

[9]Avanzi B.Strategies for dividend distribution:A review[J].North American Actuarial Journal, 2009,13(2):217–251.

[10]Albrecher H,Thonhauser S.Optimality results for dividend problems in insurance[J].RACSAM Revista de la Real Academia de Ciencias;Serie A,Matem’aticas,2009,103(2):295–320.

[11]Albrecher H,Cheung E C K,Thonhauser S.Randomized observation periods for the compound Poisson risk model:Dividends[J].Astin Bulletin,2011,41(2):645–672.

[12]Albrecher H,Cheung E C K,Thonhauser S.Randomized observation periods for the compound Poisson risk model:The discounted penalty function[J].Scandinavian Act.J.,2013,2013(6):424–452.

[13]Albrecher H,Gerber H U,Shiu E S W.The optimal dividend barrier in the Gamma-Omega model[J]. European Act.J.,2011,1(1):43–55.

[15]Avanzi B,Cheung E C K,Wong B.On a periodic dividend barrier strategy in the dual model with continuous monitoring of solvency[J].Insurance:Math.Econ.,2013,52(1):98–113.

[16]Peng Dan,Liu Donghai,Liu Zaiming.Dividend problems in the dual risk model with exponentially distributed observation time[J].Stat.Prob.Lett.,2013,83(3):841–849.

[17]Liu Xiao,Chen Zhenlong.Dividend problems in the dual model with diffusion and exponentially distributed observation time[J].Stat.Prob.Lett.,2014,87:175–183.

[18]Avanzi B,Tu V,Wong B.On optimal periodic dividend strategies in the dual model with diffusion[J]. Insurance:Math.Econ.,2014,55:210–224.

[19]Wang Cuilian,Liu Xiao.Dividend problems in the diffusion model with interest and exponentially distributed observation time[J].J.Appl.Math.,DOI:10.1155/2014/814835.

[20]Breiman L.Probability[M].Mass:Addison-Wesley,1968.

帶利率和隨機(jī)觀測時(shí)間的布朗運(yùn)動模型中最優(yōu)分紅策略

劉曉,余宏偉

(安徽師范大學(xué)數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽蕪湖241003)

本文研究了帶利率和隨機(jī)觀測時(shí)間的布朗運(yùn)動模型中的最優(yōu)分紅問題.利用隨機(jī)控制理論,獲得了最優(yōu)值函數(shù)相應(yīng)的HJB方程,表明最優(yōu)分紅策略是障礙策略,并給出了最優(yōu)值函數(shù)的顯式表達(dá)式,推廣了文獻(xiàn)[19]的結(jié)果.

分紅;破產(chǎn);HJB方程

O212.62

tion:62P05;91B30;91B70

A

0255-7797(2017)01-0039-12

?Received date:2014-10-22Accepted date:2015-01-20

Foundation item:Supported by the National Natural Science Foundation of China(11401010);the Natural Science Foundation of Education Department of Anhui Province(KJ2012ZD01);the Philosophy and Social Science Planning Foundation of Anhui Province(AHSK11-12D128);the Natural Science Foundation of Anhui Province(1308085QA14);the Research Culture Funds of Anhui Normal University (2015xmpy14).

Biography:Liu Xiao(1981–),male,born at Tianchang,Anhui,associate professor,major in stochastic control.