陳松良

(貴州師范學(xué)院數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院,貴州貴陽550018)

關(guān)于216階群的完全分類

陳松良

(貴州師范學(xué)院數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院,貴州貴陽550018)

設(shè)G為23·33階(即216階)群,本文研究G的同構(gòu)分類.利用有限群的局部分析法,證明G共有177種互不同構(gòu)的類型,并獲得了G的全部構(gòu)造.

有限群;同構(gòu)分類;群的構(gòu)造

1 引言

定理1.1設(shè)G為23·33階(即216階)群,那么G共有177種互不同構(gòu)的類型,其中

1)當(dāng)Sylow子群都正規(guī)時(shí),G恰有25個(gè)彼此不同構(gòu)的類型;

2)當(dāng)Sylow 2-子群正規(guī)但Sylow 3-子群不正規(guī)時(shí),G恰有14個(gè)彼此不同構(gòu)的類型;

3)當(dāng)Sylow 2-子群不正規(guī)但Sylow 3-子群正規(guī)時(shí),G恰有120個(gè)彼此不同構(gòu)的類型;

4)當(dāng)Sylow子群都不正規(guī)時(shí),G恰有18個(gè)彼此不同構(gòu)的類型.

2 定理的證明

以下恒設(shè)G是216階群,P是G的一個(gè)Sylow 3-子群,Q是G的一個(gè)Sylow 2-子群,我們用|G|,|g|分別表示有限群G及其元素g的階,用Cn表示n階循環(huán)群,用Epn表示pn階初等交換群,用gx表示x-1gx,其他未說明的符號(hào)見文獻(xiàn)[4].由文[5]之定理7.1.1,P必為下列5種類型之一:

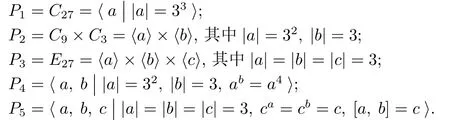
而Q也只有5種不同構(gòu)的類型:

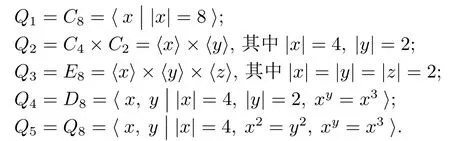
由于定理的證明較長,下面我們分為幾個(gè)引理來敘述.

引理2.1如果216階群G的Sylow子群都是正規(guī)子群,那么G恰有25個(gè)互不同構(gòu)的類型,其構(gòu)造是:G=Pi×Qj,i,j=1,2,···,5.

引理2.2如果216階群G的Sylow 2-子群正規(guī)但Sylow 3-子群不正規(guī),那么G恰有14個(gè)互不同構(gòu)的類型且它們的構(gòu)造分別是式(2.1)–(2.14),其中在式(2.1)–(2.7)中|x|=|y|=|z|=2,且〈x,y,z〉E8;而在式(2.8)–(2.14)中|x|=4,x2=y2,xy=x3,且

證這時(shí)P非平凡作用在Q上,所以有從而|Aut(Q2)|=8,|Aut(Q3)|=168,|Aut(Q4)|=8,|Aut(Q5)|=24,于是必有或即G的Sylow 2-子群是8階初等交換群或8階四元數(shù)群.又Aut(Q3)與Aut(Q5)的Sylow 3-子群都是3階循環(huán)群,所以CP(Q)必是P的一個(gè)9階正規(guī)子群.

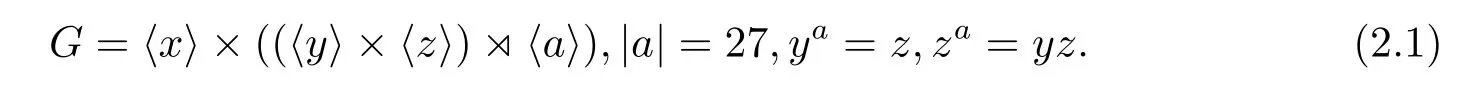
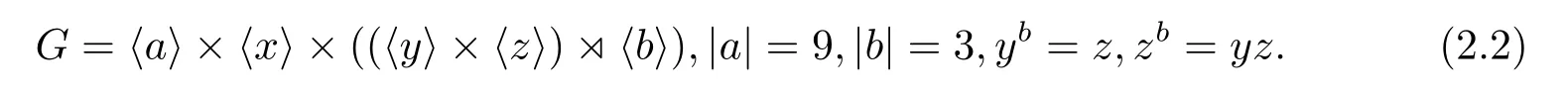
如果CP(Q)是初等交換群,則因?yàn)镻有唯一的9階初等交換子群〈a3,b〉,所以必有CP(Q)=〈a3,b〉,從而a作用在Q上是Q的一個(gè)3階自同構(gòu),因而G=〈b〉×〈Q,a〉,其構(gòu)造是

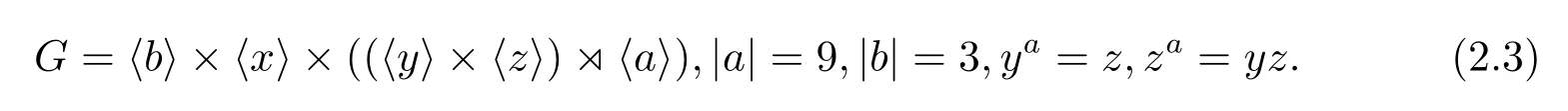
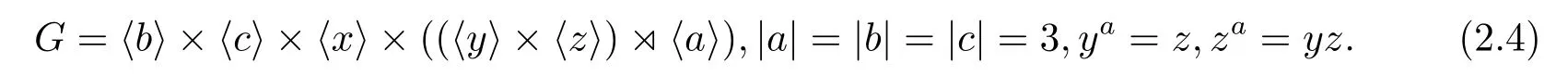
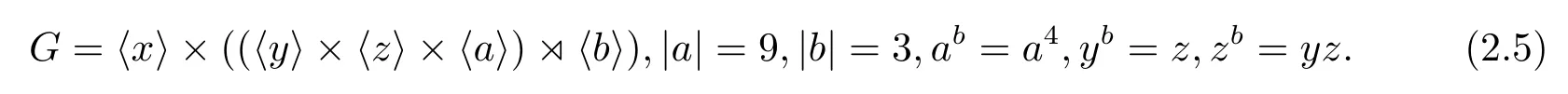
如果CP(Q)是初等交換群,則因?yàn)镻有唯一的9階初等交換子群〈a3,b〉,所以必有CP(Q)=〈a3,b〉,從而a作用在Q上是Q的一個(gè)3階自同構(gòu),因而G的構(gòu)造是

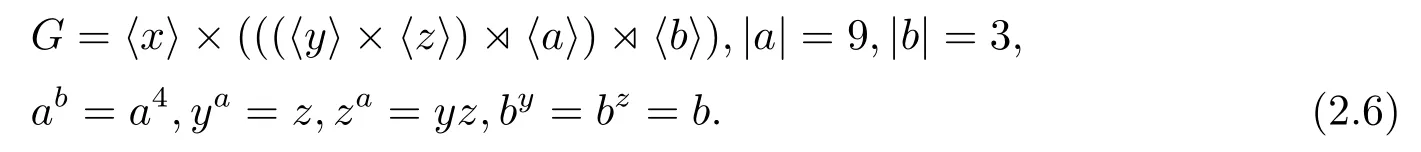
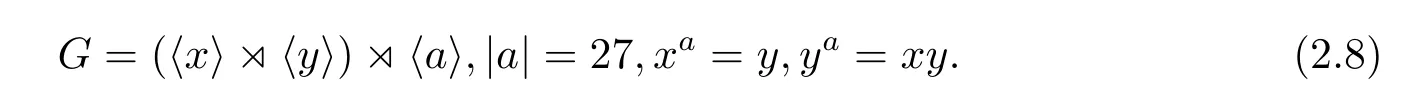
如果CP(Q)是初等交換群,則因?yàn)镻有唯一的9階初等交換子群〈a3,b〉,所以必有CP(Q)=〈a3,b〉,從而a作用在Q上是Q的一個(gè)3階自同構(gòu),因而G=〈b〉×〈Q,a〉,其構(gòu)造是

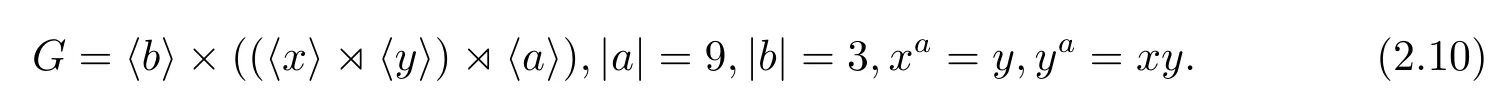
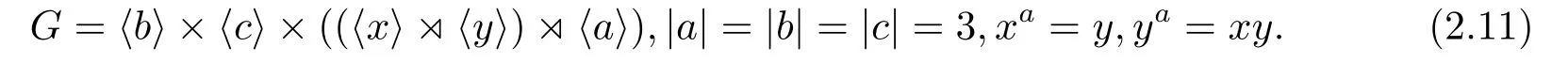
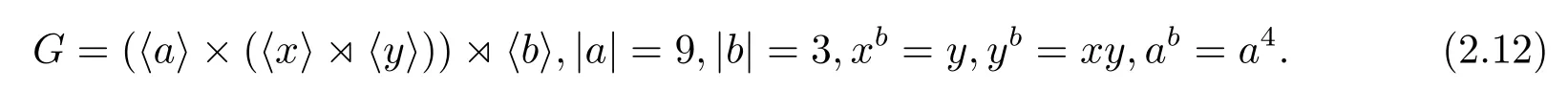
如果CP(Q)是初等交換群,則因?yàn)镻有唯一的9階初等交換子群〈a3,b〉,所以必有CP(Q)=〈a3,b〉,從而a作用在Q上是Q的一個(gè)3階自同構(gòu),因而G的構(gòu)造是

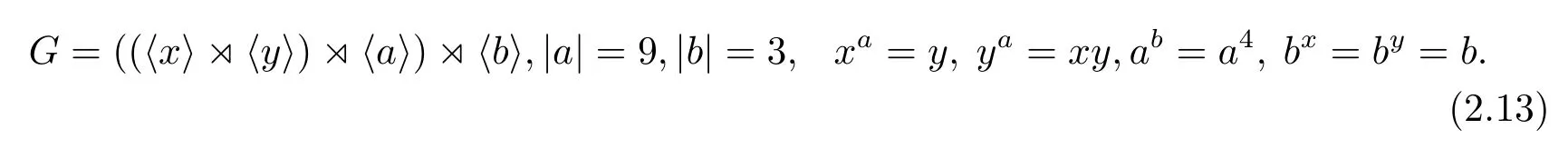
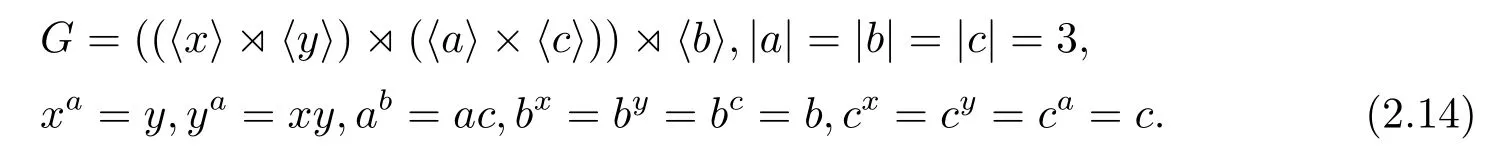
綜上所述,可知引理2.2成立.

引理2.3如果216階群G的Sylow 2-子群Q不正規(guī)但Sylow 3-子群P正規(guī),那么G恰有120個(gè)互不同構(gòu)的類型.其中當(dāng)Sylow 3-子群是循環(huán)群時(shí),G恰有7個(gè)互不同構(gòu)的類型;當(dāng)Sylow 3-子群是(32,3)型交換群時(shí),G恰有29個(gè)互不同構(gòu)的類型;當(dāng)Sylow 3-子群是27階初等交換群時(shí),G恰有52個(gè)互不同構(gòu)的類型;當(dāng)Sylow 3-子群是(32,3)型非交換群時(shí),G恰有7個(gè)互不同構(gòu)的類型;當(dāng)Sylow 3-子群是指數(shù)為3的非交換群時(shí),G恰有25個(gè)互不同構(gòu)的類型.

證類似于文獻(xiàn)[3]之引理2.4–2.8的討論,可得此引理.

注2.41)文獻(xiàn)[3]之引理2.6中(2.65)的證明有誤且漏掉了1種構(gòu)造,正確敘述如下:如果CQ(a),CQ(b),CQ(c)兩兩不等,但CQ(a)∩CQ(b)=CQ(b)∩CQ(c)=CQ(c)∩CQ(a),則不妨設(shè)CQ(a)=〈x,z〉,CQ(b)=〈y,z〉,CQ(c)=〈xy,z〉,于是G有構(gòu)造

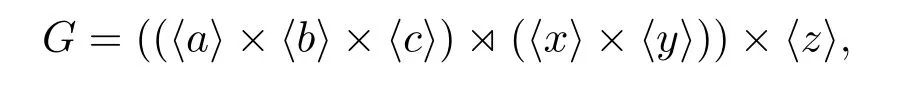
其中

如果CQ(a),CQ(b),CQ(c)中兩兩不等,且CQ(a)∩CQ(b)CQ(b)∩CQ(c),則不妨設(shè)CQ(a)∩CQ(b)=〈y〉,CQ(b)∩CQ(c)=〈z〉,于是CQ(b)=〈y,z〉.又不妨設(shè)CQ(a)=〈x,y〉,則CQ(c)∩CQ(a)=〈x〉或〈xy〉.于是CQ(c)=〈x,z〉或CQ(c)=〈xy,z〉.注意到x與xy在CQ(a)中的地位是相同的,所以不妨設(shè)CQ(c)=〈x,z〉,從而得G的構(gòu)造

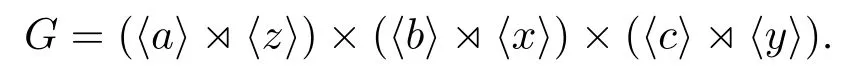
其中

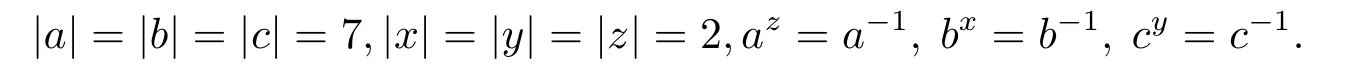
因此文[3]之引理2.6中應(yīng)當(dāng)共有52個(gè)互不同構(gòu)的類型.

2)文獻(xiàn)[3]之引理2.8中(2.118)的條件有誤,應(yīng)為“當(dāng)CQ(a)與CQ(b)中有一個(gè)是4階循環(huán)子群而另一個(gè)是4階初等交換子群時(shí)”.文[3]之引理2.8中還遺漏了G的一種構(gòu)造,即

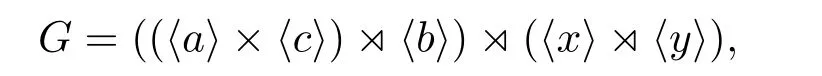
其中

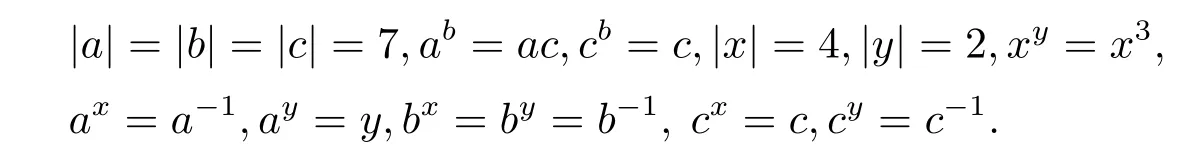
此外,文[3]之引理2.8中(ii)之(2)部分證明有誤.構(gòu)造(2.125)和(2.126)是不存在的,因?yàn)樵?2)的條件下,Q/CQ(P)只能是4階循環(huán)群,因而y在Q上的作用是平凡的,于是只能得到一種構(gòu)造

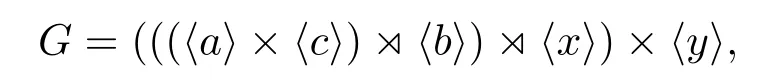
其中

故文[3]之引理2.8中只有25個(gè)互不同構(gòu)的類型.

引理2.5如果216階群G的Sylow 3-子群P與Sylow 2-子群Q都不正規(guī),那么G恰有18個(gè)互不同構(gòu)的類型.它們的構(gòu)造分別是式(2.15)–(2.32),其中在式(2.15)–(2.20)中有|x|=|y|=|z|=2;在式(2.22)–(2.32)中有|x|=|y|=|z|=2,xz=x,yz=xy;在式(2.15),(2.16),(2.19),(2.23)–(2.26),(2.30)中有|a|=9,|b|=3;在式(2.17),(2.18),(2.20), (2.21),(2.27)–(2.29),(2.31),(2.32)中有|a|=|b|=|c|=3.

證由Sylow定理[6]可知,G的Sylow 3-子群的個(gè)數(shù)是4,于是NG(P)是54階群,從而易知P在G中的核PG必是9階群,即O3(G)是9階群.又G/PG的Sylow 3-子群不正規(guī),所以G/PG同構(gòu)于一個(gè)Sylow 3-子群不正規(guī)的24階群.但Sylow 3-子群不正規(guī)的24階群只有3種不同構(gòu)的類型:(見文獻(xiàn)[5]之定理10.4.22或文獻(xiàn)[7]之定理1后的討論),于是,我們可以作下述討論.

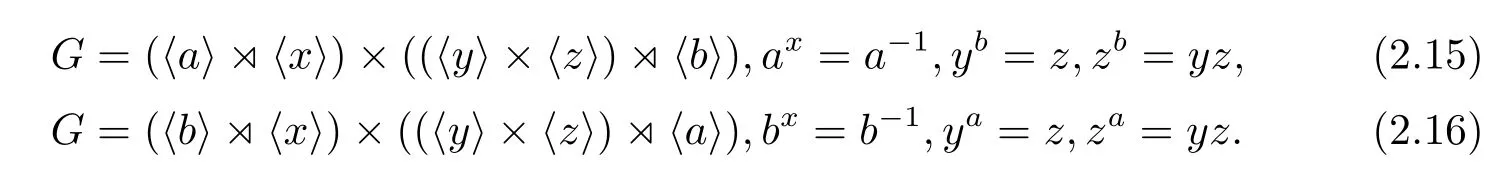
如果PG為9階初等交換群〈a3,b〉,則應(yīng)有G=其中|a|=9,|b|=3,|x|=|y|=|z|=2,ab=a4,ya=z,za=yz,yb=yx=y,zb=zx=z,于是應(yīng)有ax=a,bx=b-1.但由此就應(yīng)有a3=[a,b]x=[a,bx]=[a,b-1]=a6,這是不可能的.故此時(shí)G只有一種構(gòu)造(2.19).

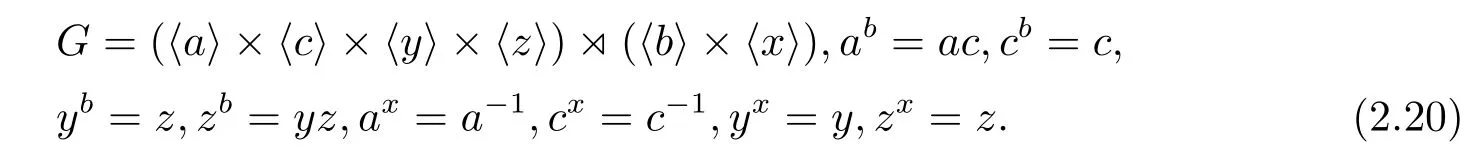
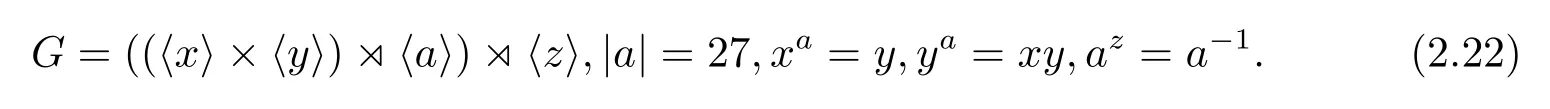
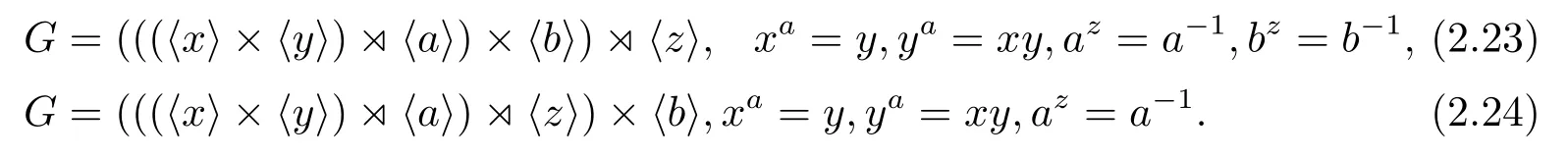
若PG是9階循環(huán)群,則G也有兩種不同的構(gòu)造

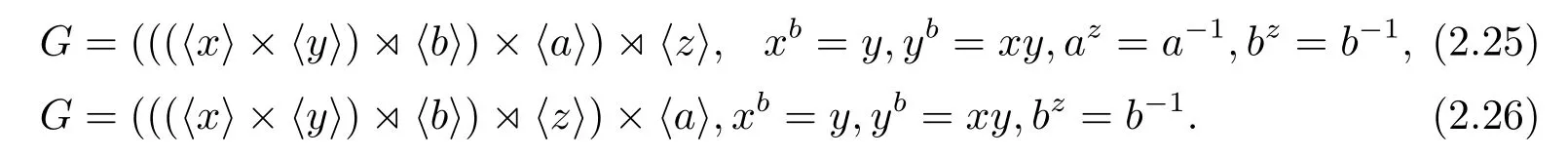
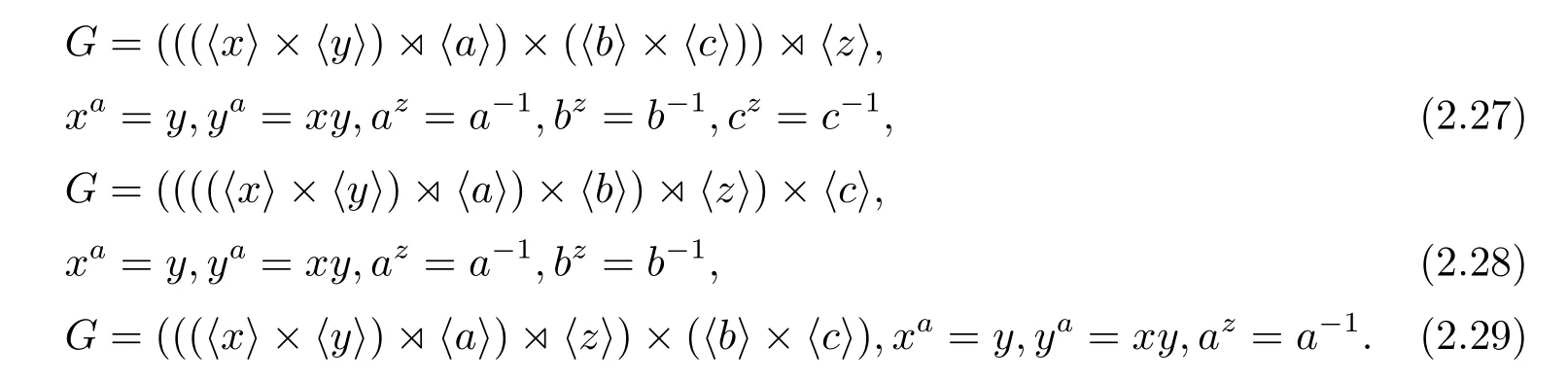
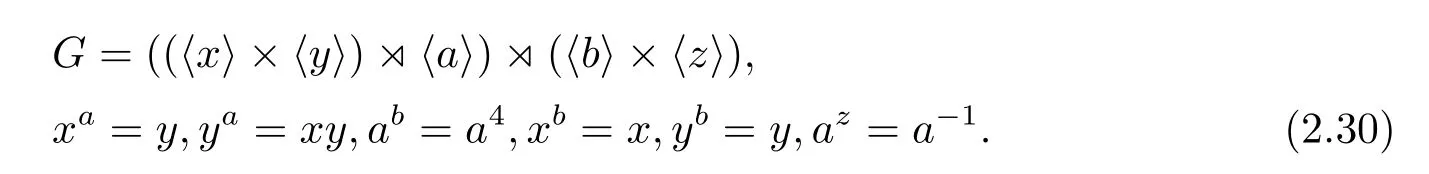
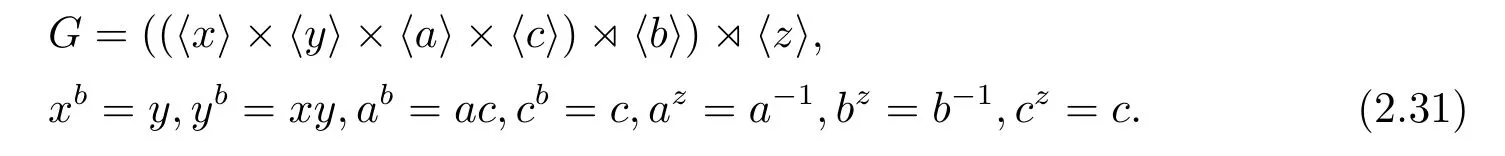
當(dāng)cz=c-1時(shí),G的構(gòu)造是

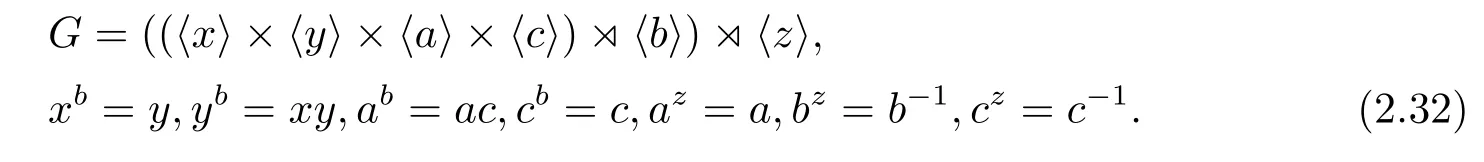
綜上所述,可知引理2.5成立.

由上面的引理2.1–2.3及引理2.5,可知定理1.1成立.

[1]肖文俊,譚忠.階為23p3的群的構(gòu)造[J].廈門大學(xué)學(xué)報(bào)(自然科學(xué)版),1995,34(5):845–846.

[2]蔡瓊.23p3階群的構(gòu)造[J].數(shù)學(xué)雜志,2005,25(4):449–452.

[3]陳松良.2744階群的構(gòu)造[J].數(shù)學(xué)學(xué)報(bào)(中文版),2013,56(6):993–1008.

[4]Robinson D J S.A course in the theory of groups[M].New York,Heidelberg,Berlin:Springer-Verlag, 1982.

[5]張遠(yuǎn)達(dá).有限群構(gòu)造[M].北京:科學(xué)出版社,1982.

[6]徐明曜.有限群導(dǎo)引(上冊(cè))[M].北京:科學(xué)出版社,1999.

[7]陳松良,歐陽建新,李驚雷.pq3階群的完全分類[J].海南師范大學(xué)學(xué)報(bào)(自然科學(xué)版),2010,23(3): 253–255.

[8]陳松良,蔣啟燕.關(guān)于108階群的完全分類[J].鄭州大學(xué)學(xué)報(bào)(理學(xué)版),2013,45(1):10–14.

[9]黃強(qiáng).2332階群的構(gòu)造[J].數(shù)學(xué)雜志,1986,6(1):51–58.

ON THE STRUCTURES OF FINITE GROUPS OF ORDER 216

CHEN Song-liang
(School of Mathematics and Computer Science,Guizhou Normal College,Guiyang 550018,China)

Let G be finite groups of order 216(i.e.,23·33).By means of local analysis of finite groups,we study the isomorphic classifications of G and have showed that G has 177 nonisomorphic types and their structures are all laid out.

finite group;isomorphic classification;structure of group

tion:20B05;20D25;20E34

O152.1

A

0255-7797(2017)01-0185-08

2014-01-13接收日期:2014-09-09

貴州師范學(xué)院重點(diǎn)支持學(xué)科項(xiàng)目;貴州省自然科學(xué)基金資助項(xiàng)目(黔科合J字[2012]2289; [2013]2234).

陳松良(1964–),男,湖南雙峰,教授,主要研究方向:代數(shù)學(xué)及其應(yīng)用.