Bashir AHMAD

Nonlinear Analysis and Applied Mathematics(NAAM)-Research Group,Department of Mathematics, Faculty of Science,King Abdulaziz University,P.O.Box 80203,Jeddah 21589,Saudi Arabia

Sotiris K.NTOUYAS?

Department of Mathematics,University of Ioannina,451 10 Ioannina,Greece;

Nonlinear Analysis and Applied Mathematics(NAAM)-Research Group,Department of Mathematics, Faculty of Science,King Abdulaziz University,P.O.Box 80203,Jeddah 21589,Saudi Arabia

Jessada TARIBOON

Nonlinear Dynamic Analysis Research Center,Department of Mathematics,Faculty of Applied Science,King Mongkut’s University of Technology North Bangkok,Bangkok 10800,Thailand

A NONLOCAL HYBRID BOUNDARY VALUE PROBLEM OF CAPUTO FRACTIONAL INTEGRO-DIFFERENTIAL EQUATIONS?

Bashir AHMAD

Nonlinear Analysis and Applied Mathematics(NAAM)-Research Group,Department of Mathematics, Faculty of Science,King Abdulaziz University,P.O.Box 80203,Jeddah 21589,Saudi Arabia

E-mail:bashirahmad?qau@yahoo.com

Sotiris K.NTOUYAS?

Department of Mathematics,University of Ioannina,451 10 Ioannina,Greece;

Nonlinear Analysis and Applied Mathematics(NAAM)-Research Group,Department of Mathematics, Faculty of Science,King Abdulaziz University,P.O.Box 80203,Jeddah 21589,Saudi Arabia

E-mail:sntouyas@uoi.gr

Jessada TARIBOON

Nonlinear Dynamic Analysis Research Center,Department of Mathematics,Faculty of Applied Science,King Mongkut’s University of Technology North Bangkok,Bangkok 10800,Thailand

E-mail:jessadat@kmutnb.ac.th

In this paper,we discuss the existence of solutions for a nonlocal hybrid boundary value problem of Caputo fractional integro-diferential equations.Our main result is based on a hybrid fxed point theorem for a sum of three operators due to Dhage,and is well illustrated with the aid of an example.

Caputo fractional derivative;integral;hybrid;fxed point theorem

2010 MR Subject Classifcation34A08;34A12

1 Introduction

Fractional diferential equations arise in the mathematical modeling of systems and processes occurring in many engineering and scientifc disciplines such as physics,chemistry,aerodynamics,electrodynamics of complex medium,polymer rheology,economics,control theory, signal and image processing,biophysics,blood fow phenomena,etc.[1–3].For some recent development on the topic,see[4–16]and the references therein.

Hybrid fractional diferential equations were also studied by several researchers.This class of equations involves the fractional derivative of an unknown function hybrid with the nonlinearity depending on it.Some recent results on hybrid diferential equations can be found in a series of papers(see[17–21]).

In this paper we study the existence of solutions for a nonlocal boundary value problem of hybrid fractional integro-diferential equations given by

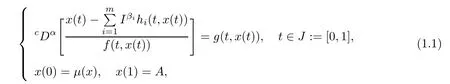
wherecDαdenotes the Caputo fractional derivative of order α,1<α≤2,Iφis the Riemann-Liouville fractional integral of order φ>0,φ∈{β1,β2,···,βm},f∈C(J×R,R{0}), g∈C(J×R,R),hi∈C(J×R,R),0<βi,i=1,2,···,m,μ:C([0,1],R)→R and A∈R.

The rest of the paper is organized as follows.In Section 2,we recall some useful preliminaries.Section 3 contains the main result which is obtained by means of a hybrid fxed point theorem for three operators in a Banach algebra due to Dhage[22].Also see the papers[23,24]. An example is also discussed for illustration of the main result.

2 Preliminaries

In this section,we introduce some notations and defnitions of fractional calculus[1,2]and present preliminary results needed in our proofs later.

Defnition 2.1For(n?1)-times absolutely continuous function g:[0,∞)→ R,the Caputo derivative of fractional order q is defned as

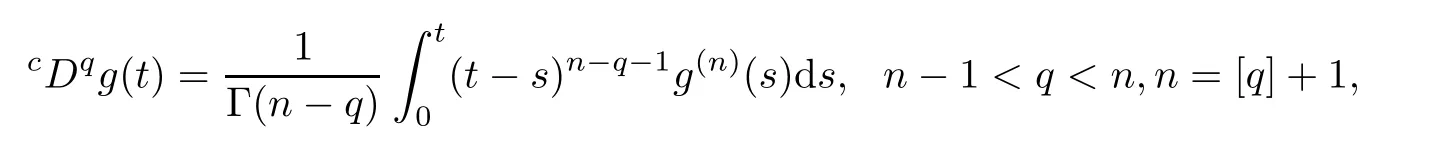
where[q]denotes the integer part of the real number q.

Defnition 2.2The Riemann-Liouville fractional integral of order p>0 of a continuous function f:(0,∞)→R is defned by

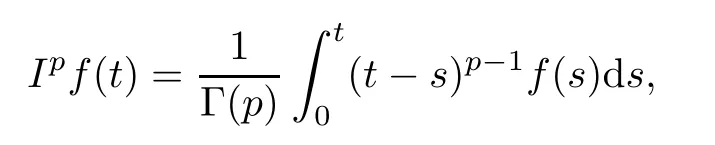
provided the right-hand side is point-wise defned on(0,∞).

Defnition 2.3The Caputo derivative of order q for a function f:[0,∞)→R can be written as

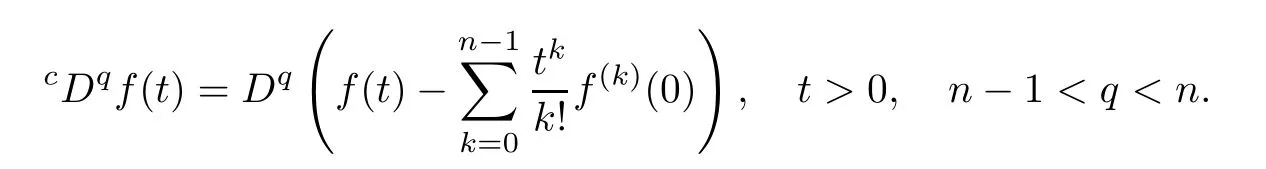
Remark 2.4If f(t)∈Cn[0,∞),then

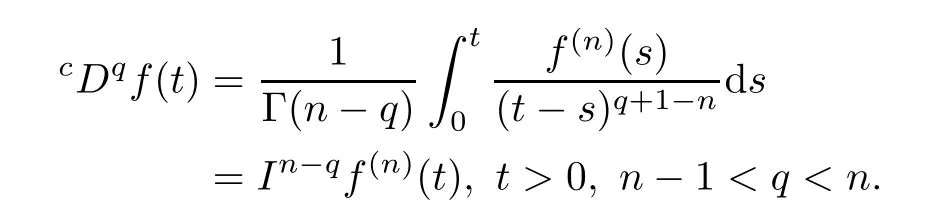
Lemma 2.5(see[1]) Let x∈Cm[0,1]and y∈AC[0,1].Then,for q∈(m?1,m),m∈N and t∈[0,1],

(a)the general solution of the fractional diferential equationcDqx(t)=0 is

x(t)=k0+k1t+k2t2+···+km?1tm?1,where ki∈R,i=0,1,2,···,m?1;

(c)cDqIqy(t)=y(t).

We denote by E=C(J,R)the space of continuous real-valued functions defned on J= [0,1].Defne a norm k·k and a multiplication in E by

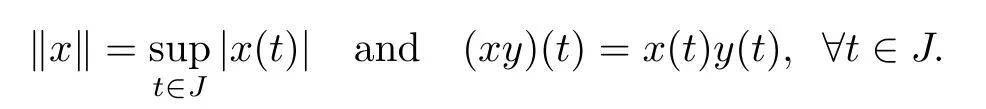
Clearly E is a Banach algebra with respect to above supremum norm and the multiplication in it.

3 Main Result

The following hybrid fxed point theorem for three operators in a Banach algebra E due to Dhage[22]will be used to prove the existence result for the nonlocal boundary value problem (1.1).

Lemma 3.1Let S be a nonempty,closed convex and bounded subset of a Banach algebra E and let A,C:E→E and B:S→E be three operators such that

(a1)A and C are Lipschitzian with Lipschitz constants δ and ρ,respectively; (b1)B is compact and continuous;

(c1)x=AxBy+Cx?x∈S for all y∈S; (d1)δM+ρ<1,where M=kB(S)k.

Then the operator equation x=AxBx+Cx has a solution.

Lemma 3.2Let y∈AC([0,1],R).Then x is a solution of the hybrid fractional integrodiferential problem

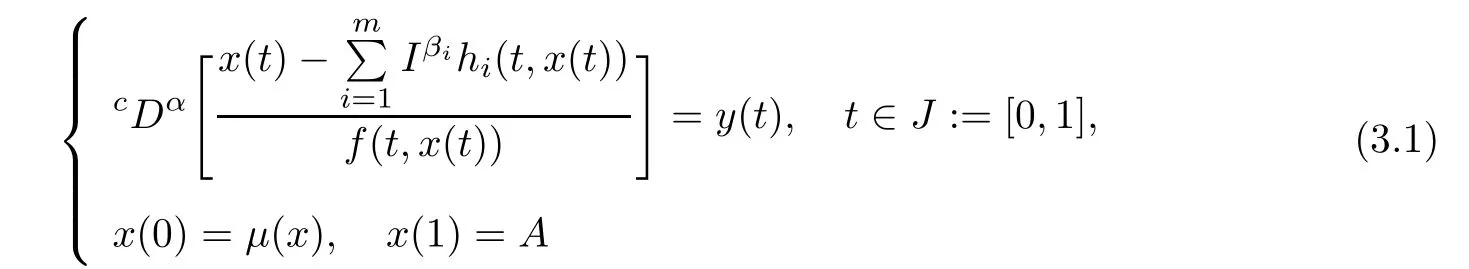
if and only if

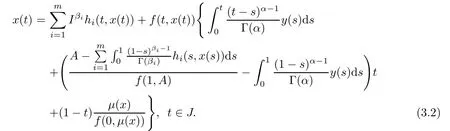
ProofApplying the Riemann-Liouville fractional integral of order α to both sides of(3.1) and using Lemma 2.5,we have

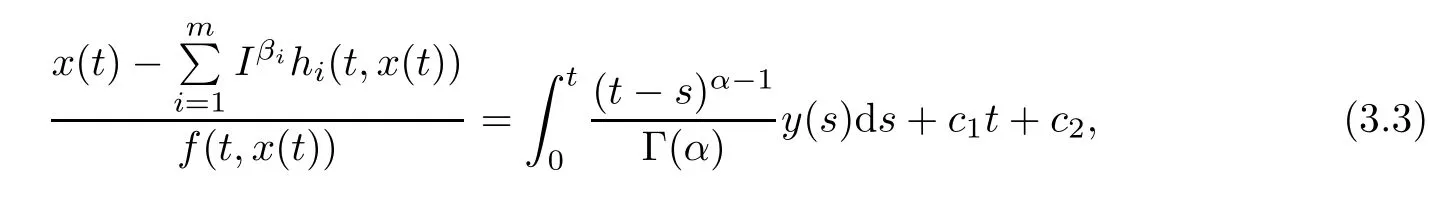
where c1,c2∈R.Using the given boundary conditions,we fnd that

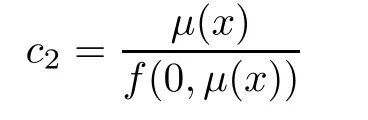
and

Substituting the values of c1,c2in(3.3),we get solution(3.2).The converse follows by direct computation.This completes the proof.

In the sequel,we need the following assumptions.

(H1)The functions f:J×R→ R{0}and hi:J×R→ R,i=1,2,···,m,are continuous and there exist positive functions φ,ψi,i=1,2,···,m,with bounds kφk and kψik, i=1,2,···,m,respectively,such that

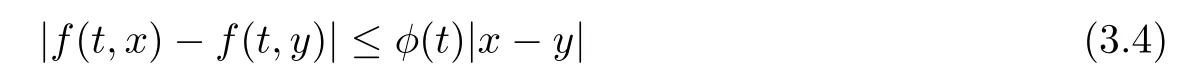
and

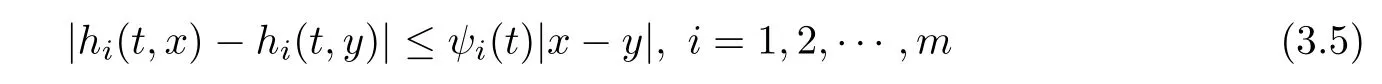
for t∈J and x,y∈R.

(H2)There exists a function p∈C(J,R+)and a continuous nondecreasing function Ψ: [0,∞)→(0,∞)such that

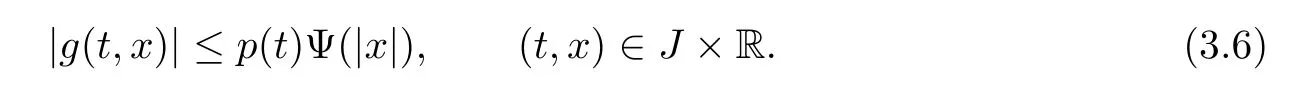
(H3)There exists a constant M0>0 such that

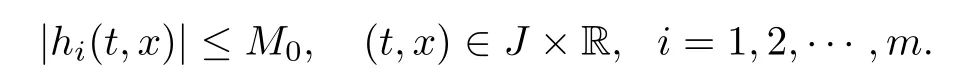
(H4)There exists a constant M1>0 such that

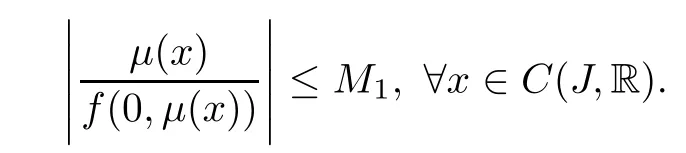
(H5)There exists a number r>0 such that

Theorem 3.3Assume that conditions(H1)–(H5)hold.Then there exists at least one solution for the nonlocal problem(1.1)on J.

ProofWe consider a subset S of E given by

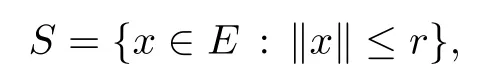
where r satisfes inequality(3.7).Notice that S is closed,convex and bounded subset of the Banach space E.In view of Lemma 3.2,we defne an operator

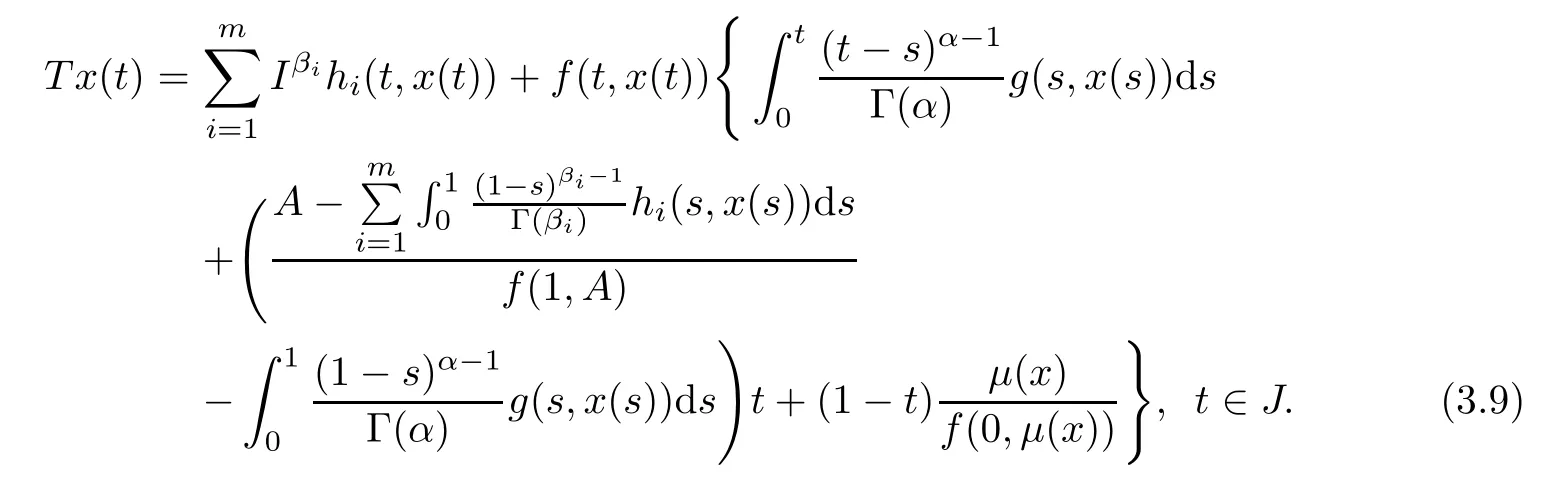
Notice that the fxed point problem Tx=x is equivalent to problem(1.1).Next we introduce three operators A:E→E,B:S→E and C:E→E as follows:

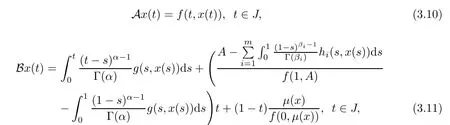
and

Observe that Tx=AxBx+Cx.Now,we show that the operators A,B and C satisfy all the conditions of Lemma 3.1 in a series of steps.

Step 1We frst show that A and C are Lipschitzian on E.

Let x,y∈E.Then by(H1),for t∈J,we have

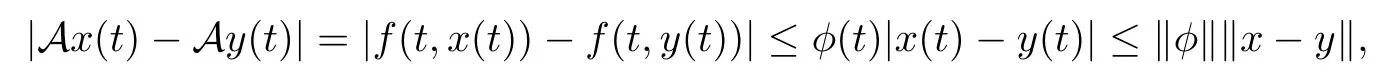
which implies kAx?Ayk≤kφkkx?yk for all x,y∈E.Therefore,A is a Lipschitzian on E with Lipschitz constant kφk.

Analogously,for any x,y∈E,we have

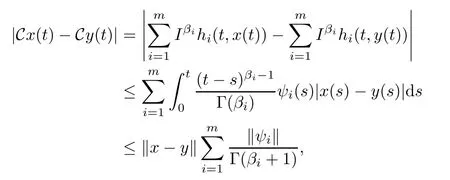
which implies that

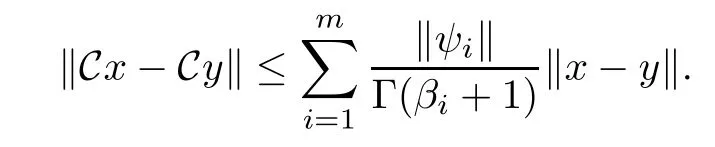
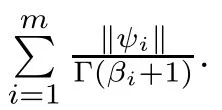
Step 2The operator B is completely continuous on S.

We frst show that the operator B is continuous on E.Let{xn}be a sequence in S converging to a point x∈S.Then by Lebesgue dominated convergence theorem,for all t∈J, we obtain

This implies that Bxn→ Bx point-wise on J.Further it can be shown that{Bxn}is an equicontinuous sequence of functions.So Bxn→ Bx uniformly and the operator B is continuous on S.

Next we will prove that the set B(S)is uniformly bounded in S.For any x∈S,we have

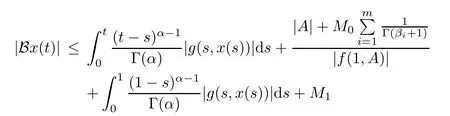
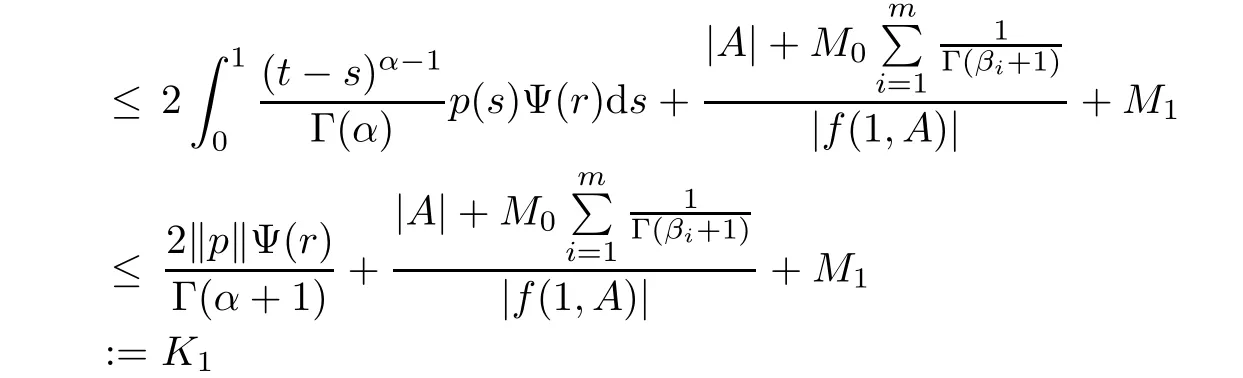
for all t∈J.Therefore,kBk≤K1which shows that B is uniformly bounded on S.

Now,we will show that B(S)is an equicontinuous set in E.Let τ1,τ2∈J with τ1<τ2and x∈S.Then we have

which is independent of x∈S.As τ1→τ2,the right-hand side of the above inequality tends to zero.Therefore,it follows from the Arzel′a-Ascoli theorem that B is a completely continuous operator on S.

Step 3Hypothesis(c1)of Lemma 3.1 is satisfed.

Let x∈E and y∈S be arbitrary elements such that x=AxBy+Cx.Then we have

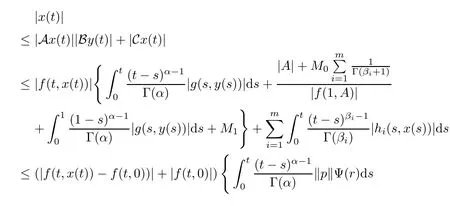
which leads to

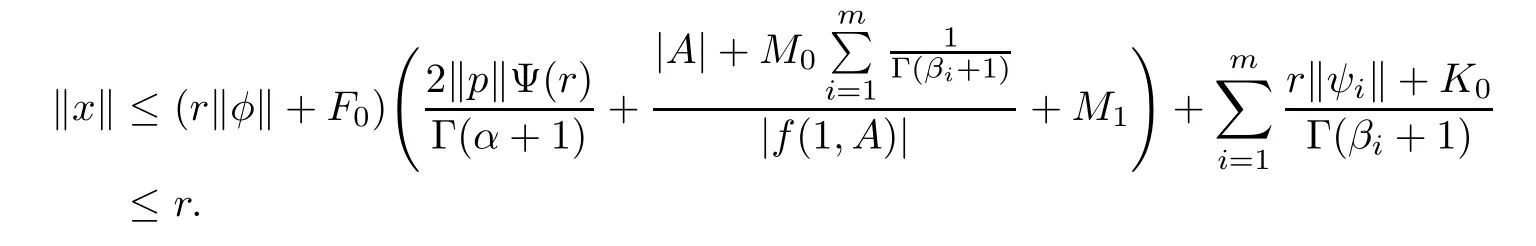
Therefore,x∈S.

Step 4Finally we show that δM+ρ<1,that is,(d1)of Lemma 3.1 holds.

Since

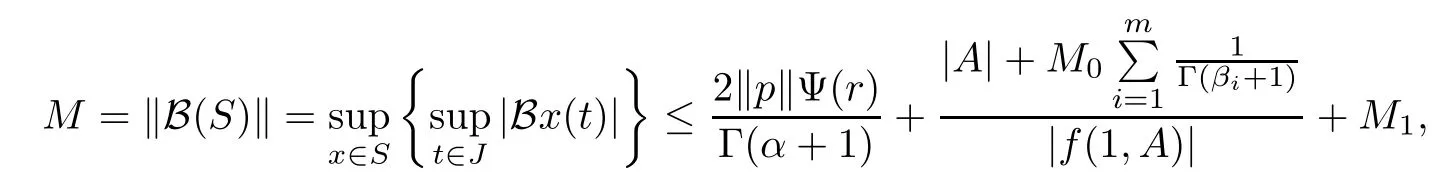
therefore,by(H4,)we have

Thus all the conditions of Lemma 3.1 are satisfed and hence the operator equation x= AxBx+Cx has a solution in S.In consequence,problem(1.1)has a solution on J.This completes the proof.

Example 3.4Consider the following nonlocal hybrid boundary value problem

where 0<γ<1,ξj∈(0,1),ξj<ξj+1,j=1,2,···,n?2,n≥3,

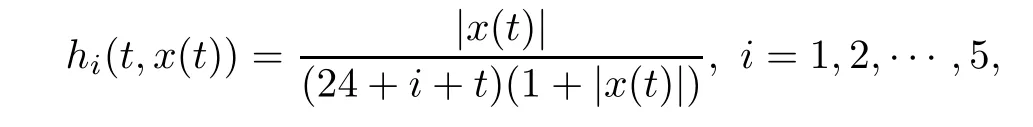
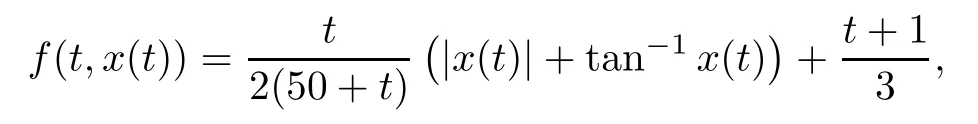
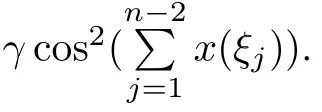
Setting φ(t)=t/(50+t)and ψ(t)=1/(24+i+t),we get kφk=1/51 and kψik=1/(24+i), i=1,2,···,5.It is easy to see that

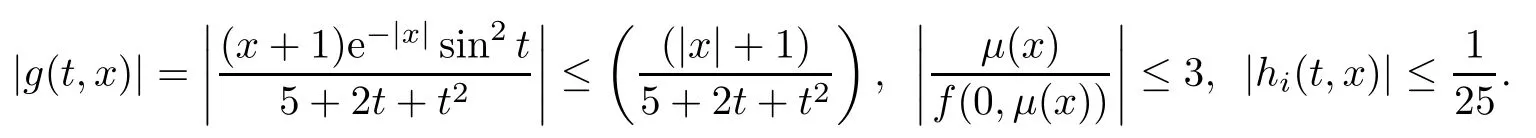
[1]Kilbas A A,Srivastava H M,Trujillo J J.Theory and Applications of Fractional Diferential Equations, North-Holland Mathematics Studies,204.Amsterdam:Elsevier Science B V,2006

[2]Podlubny I.Fractional Diferential Equations.San Diego:Academic Press,1999

[3]Sabatier J,Agrawal O P,Machado J A T,eds.Advances in Fractional Calculus:Theoretical Developments and Applications in Physics and Engineering.Dordrecht:Springer,2007

[4]Ahmad B.Existence of solutions for irregular boundary value problems of nonlinear fractional diferential equations.Appl Math Lett,2010,23:390–394

[5]Ahmad B,Ntouyas S K.A four-point nonlocal integral boundary value problem for fractional diferential equations of arbitrary order.Electron J Qual Theory Difer Equ,2011,(22):15

[6]Liang S,Zhang J.Existence of multiple positive solutions for m-point fractional boundary value problems on an infnite interval.Math Comput Modelling,2011,54:1334–1346

[7]Bai Z,Sun W.Existence and multiplicity of positive solutions for singular fractional boundary value problems.Comput Math Appl,2012,63:1369–1381

[8]Agarwal R P,O’Regan D,Stanek S.Positive solutions for mixed problems of singular fractional diferential equations.Math Nachr,2012,285:27–41

[9]Graef J R,Kong L.Existence of positive solutions to a higher order singular boundary value problem with fractional Q-derivatives.Fract Calc Appl Anal,2013,16:695–708

[10]O’Regan D,Stanek S.Fractional boundary value problems with singularities in space variables.Nonlinear Dynam,2013,71:641–652

[11]Thiramanus P,Ntouyas S K,Tariboon J.Existence and uniqueness results for Hadamard-type fractional diferential equations with nonlocal fractional integral boundary conditions.Abstr Appl Anal,2014,2014: Article ID 902054

[12]Tariboon J,Ntouyas S K,Sudsutad W.Fractional integral problems for fractional diferential equations via Caputo derivative.Adv Difer Equ,2014,2014:181

[13]Ahmad B,Ntouyas S K.Nonlocal fractional boundary value problems with slit-strips boundary conditions. Fract Calc Appl Anal,2015,18:261–280

[14]Henderson J,Luca R,Tudorache A.On a system of fractional diferential equations with coupled integral boundary conditions.Fract Calc Appl Anal,2015,18:361–386

[15]Ding Y,Wei Z,Xu J,O’Regan D.Extremal solutions for nonlinear fractional boundary value problems with p-Laplacian.J Comput Appl Math,2015,288:151–158

[16]Zhang L,Ahmad B,Wang G.Successive iterations for positive extremal solutions of nonlinear fractional diferential equations on a half line.Bull Aust Math Soc,2015,91:116–128

[17]Zhao Y,Sun S,Han Z,Li Q.Theory of fractional hybrid diferential equations.Comput Math Appl,2011, 62:1312–1324

[18]Sun S,Zhao Y,Han Z,Li Y.The existence of solutions for boundary value problem of fractional hybrid diferential equations.Commun Nonlinear Sci Numer Simul,2012,17:4961–4967

[19]Ahmad B,Ntouyas S K.An existence theorem for fractional hybrid diferential inclusions of Hadamard type with Dirichlet boundary conditions.Abstr Appl Anal,2014,2014:Article ID 705809

[20]Dhage B C,Ntouyas S K.Existence results for boundary value problems for fractional hybrid diferential inclusions.Topol Methods Nonlinar Anal,2014,44:229–238

[21]Ahmad B,Ntouyas S K,Alsaedi A.Existence results for a system of coupled hybrid fractional diferential equations.Sci World J,2014,2014:Article ID 426438

[22]Dhage B C.A fxed point theorem in Banach algebras with applications to functional integral equations. Kyungpook Math J,2004 44:145–155

[23]Dhage B C.Quadratic perturbations of periodic boundary value problems of second order ordinary diferential equations.Difer Equ Appl,2010,2:465–486

[24]Dhage B C.Basic results in the theory of hybrid diferential equations with mixed perturbations of second type.Funct DifEqu,2012,19:1–20

?Received July 4,2015;revised April 29,2016.

?Corresponding author:Sotiris K.NTOUYAS.