LI Kai-peng,WANG Xu-sheng

(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)

TOTALLY UMBILICAL SUBMANIFOLD ON RIEMANNIAN MANIFOLD WITH AN ORTHOGONAL CONNECTION

LI Kai-peng,WANG Xu-sheng

(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)

In this paper,we investigate the fundamental equations of submanifolds under orthogonal connections and apply the results in totally umbilical submanifolds.By using the method of Cartan to split the torsion tensor into three components,we calculate and attain the fundamental equations.We consider a special orthogonal connection with which the Riemannian curvature has the same properties as the Levi-Civita connection.We use the fundamental equations to argue totally umbilical submanifolds on spaces with constant curvature,which generalizes the results under the Levi-Civita connection.

orthogonal connections;fundamental equations in Riemannian manifolds;submanifold;umbilical point

1 Introduction

Orthogonal connections are affine connections compatible with the metric.Cartan researched general orthogonal connections in the 1920s.An orthogonal connection minus the Levi-Civita equals a tensor which is called torsion.Cartan found that in general the torsion tensor can split into three components：the vectorial torsion,the totally anti-symmetric one and the one of Cartan-type.Taking the scalar curvature of orthogonal connections one attains the Einstein-Cartan-Hilbert functional.Its critical points are Einstein manifolds,in particular the torsion of a critical point is zero.

We review Cartan’s classi fi cation and Einstein-Cartan theory in Section 2.Under an orthogonal connection,in general,the Bianchi identity is not always hold,so many properties are not as brief as the Levi-Civita connection.We try to fi nd an orthogonal connection which is not the Levi-Civita connection satisfying the Bianchi identity.In this paper,we focus on totally umbilical submanifold in a constant curvature space.We calculate the fundamental equations,and want to use the Causs equation to express the curvature and investigate thetotally umbilical submanifold under an orthogonal connection.To read more results about orthogonal connections,especially properties on subminifolds,please refer to our other work.

2 Preliminaries

We consider ann-dimensional manifoldMequipped with some Riemannian metricg.Let?denote the Levi-Civita connection on the tangent bundle.For any affine connection?′on the tangent bundle there exists a(2,1)-tensor fi eldAsuch that

for all vector fi eldsX,Y.

In this article we will require all connections?′to be orthogonal,i.e.,for all vector

fieldsX,Y,Z,one has

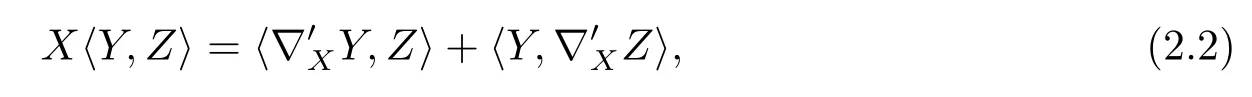
where 〈·,·〉denotes the scalar product given by the Riemannian metricg.For any tangent vectorXone gets from(2.1)and(2.2)that the endomorphismA(X,·)is skew-adjoint

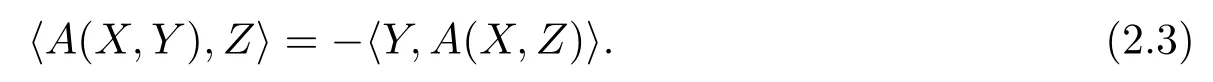
Next,we want to express some curvature quantities for?′in terms ofAand curvature quantities for?.To that end we fi x some pointp∈M,and we extend any tangent vectorsX,Y,Z,W∈TpMto vector fi elds again denoted byX,Y,Z,Wbeing synchronous inp,which means

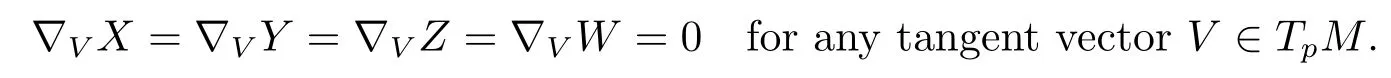
Furthermore,we choose a local orthogonal frame of vector fi eldsE1,···,Enon a neighbourhood ofp,all being synchronous inp,then the Lie bracket[X,Y]=?XY-?YX=0 vanishes inp,and synchronicity inpimplies

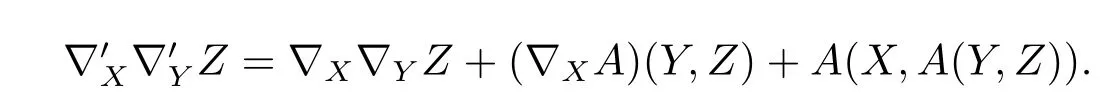
Hence,inpthe Riemann tensor of?′reads as

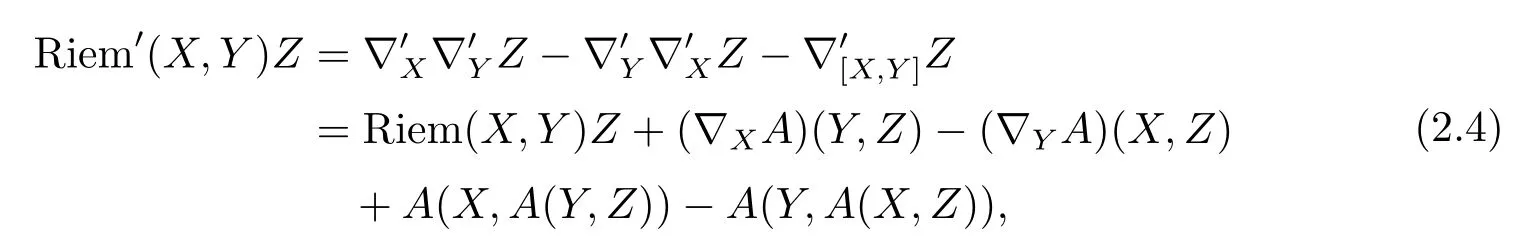
where Riem′denotes the Riemann tensor of?.We note that Riem′(X,Y)Zis anti-symmetric inXandY.And by di ff erentiation of(2.3)we get that(?EiA)(Ej,·)and(?EjA)(Ei,·)are skewadjoint,and therefore we have

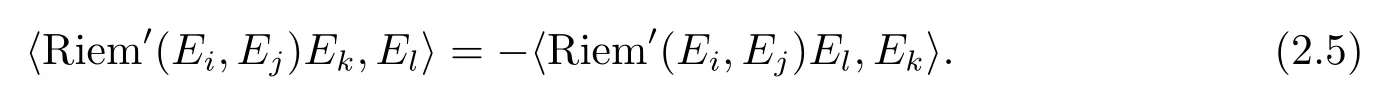
In general,Riem′does not satisfy the Bianchi identity.The Ricci curvature of?′is defined as

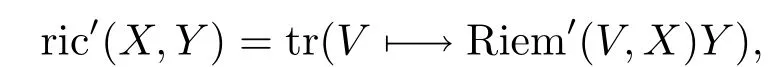
by(2.4)this can be expressed as

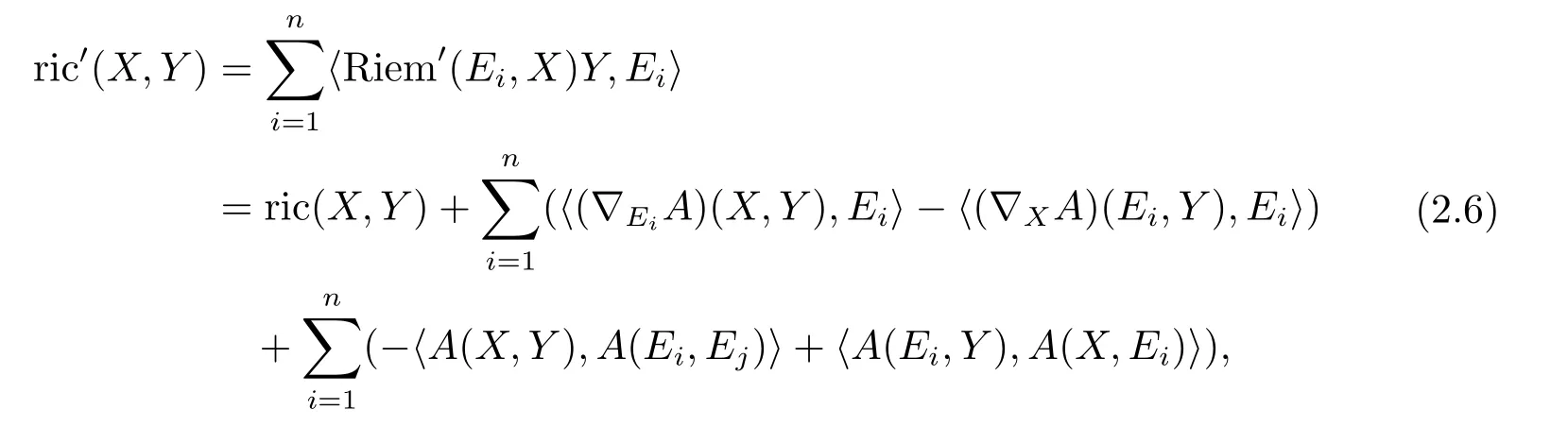
where ric′is the Ricci curvature of?′.We have used thatA(Ei,·)andA(X,·)are skewadjoint.

One obtains the scalar curvatureR′of?′by taking yet another trace,inpit is given asFor the following calculation we use that(?VA)(X,·)is skew-adjoint for any tangent vectorsV,X,and we get

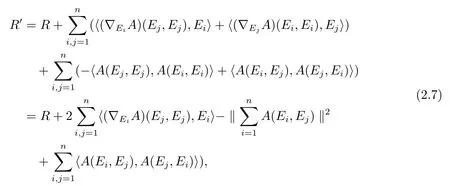
whereRdenotes the scalar curvature of?.

From(2.3)we know that the torsion tensorA(X,·)is skew-adjoint on the tangent spaceTpM.Any torsion tensorAinduces a(3,0)-tensor by setting

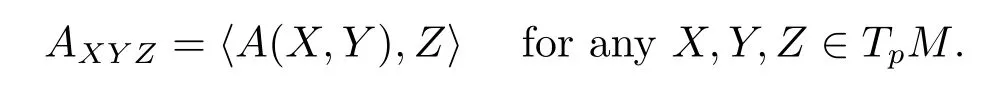
We define the space of all possible torsion tensors onTpMby

This vector space carries a scalar product

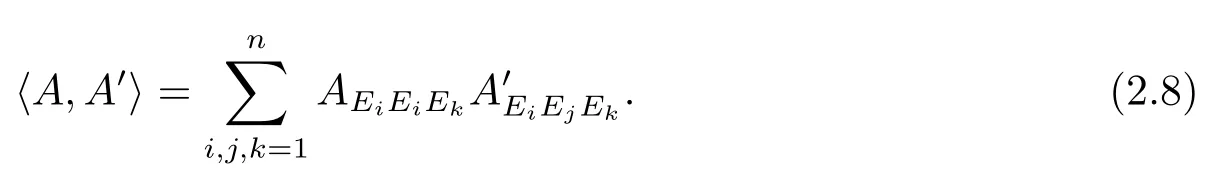
ForA∈Υ(TpM)andZ∈TpMone denotes the trace over the fi rst two entries by

Using the de fi nition of inner product of tensors,we denote

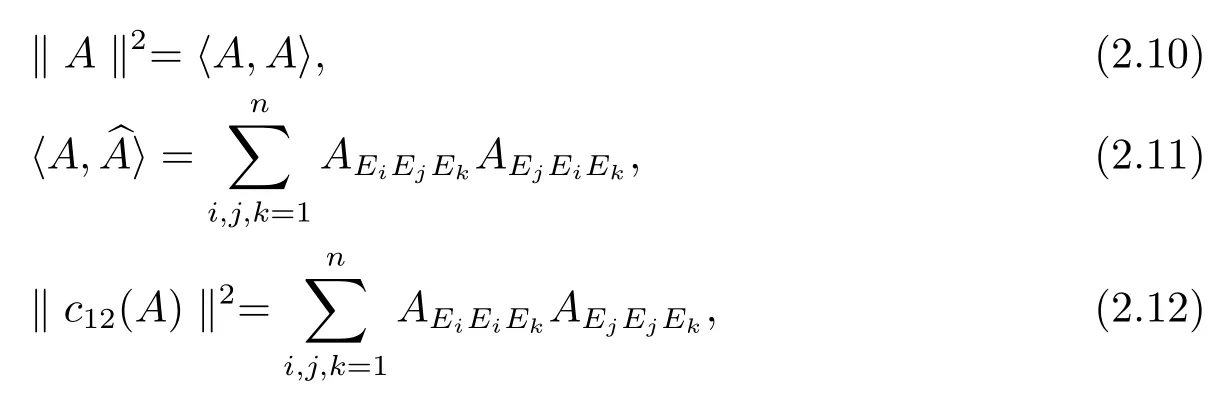
Theorem 2.1For dim(M)≥ 3,one has the following decomposition of(TpM)into irreducibleO(TpM)-subrepresentations

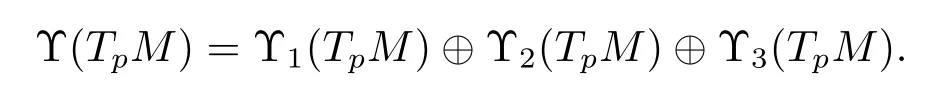
This decomposition is orthogonal with respect to 〈·,·〉,and it is given by

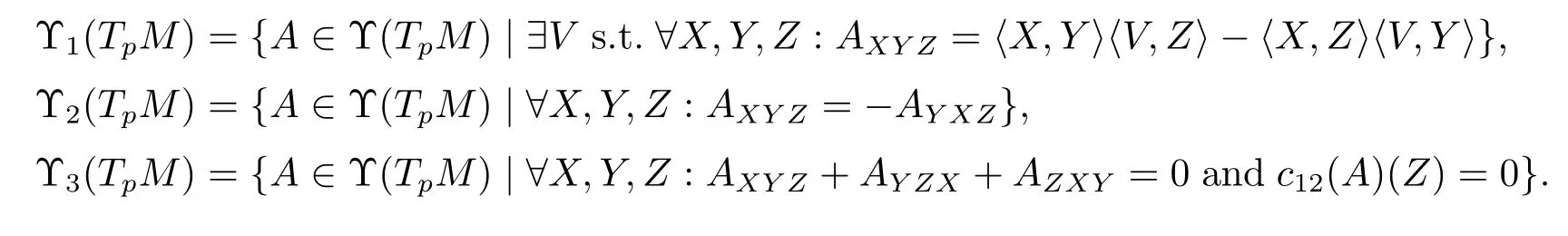
For dim(M)=2 theO(TpM)-representation(TpM)=1(TpM)is irreducible.

ProofStep 1Proof the decomposition exists.

Suppose anyA∈(TpM),A=A(1)+A(2)+A(3),A(i)∈i(TpM),i=1,2,3.We denoteAEiEjEkbyAijk,and denote〈Ei,Ej〉byδij,therefore

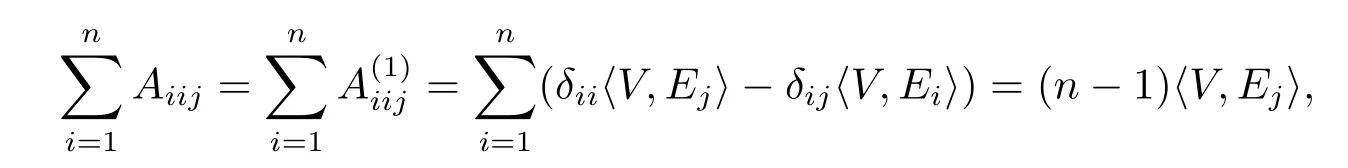
we get

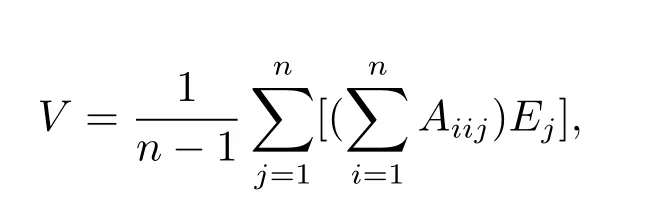
soA(1)can be con fi rmed.Thenhence

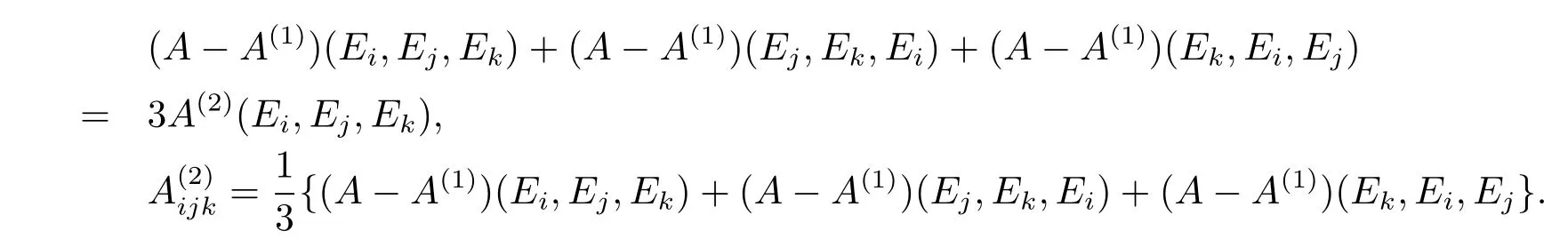
ThereforeA(2)is con fi rmed.

We need to ensure thatA(3)=A-A(1)-A(2)is a Cartan-type.

For anyX,Y,Z∈TpM,since,we have

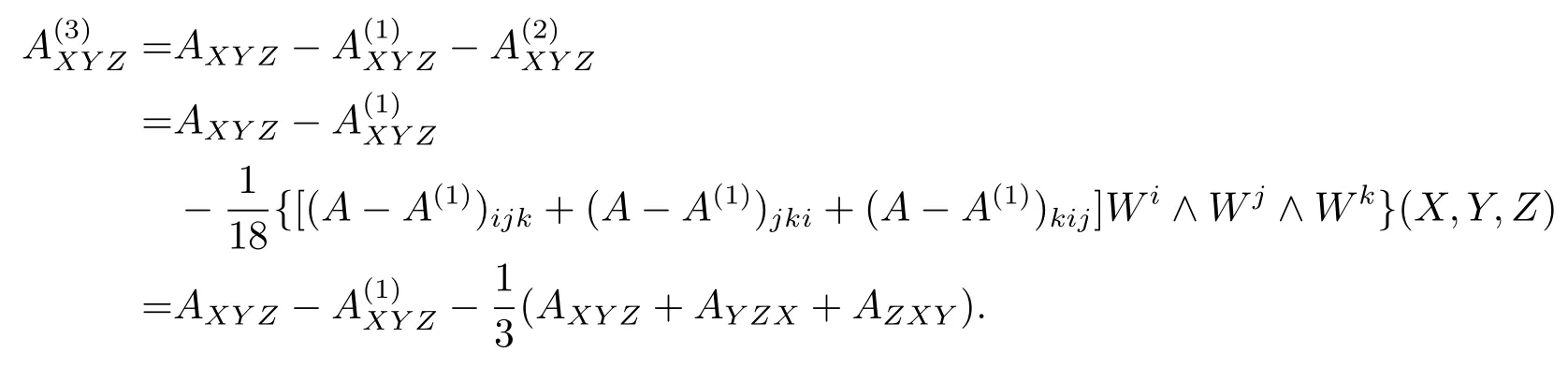
In the same way,

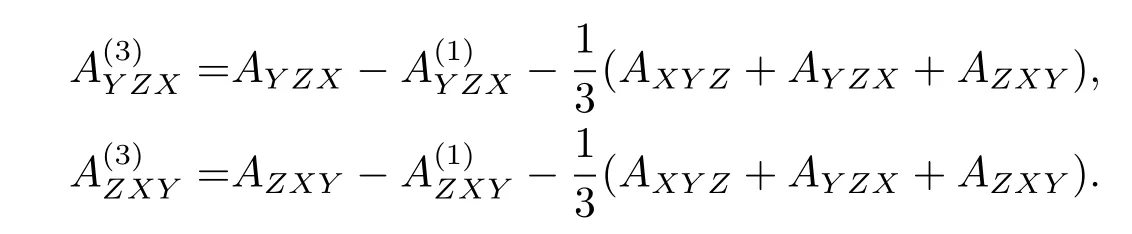
Add the two sides of the equations,we get,consider

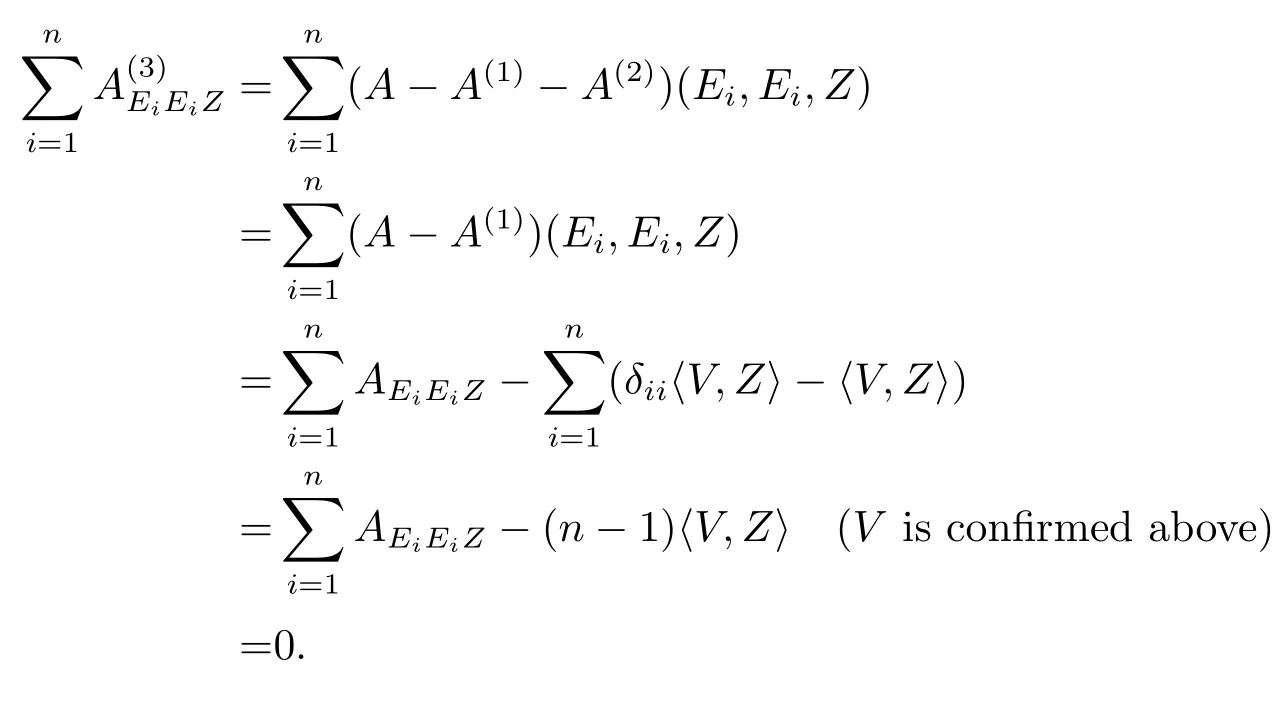
Hence the decomposition exists.

Step 2The decomposition is unique.

LetA=0∈(TpM),ifA=A(1)+A(2)+A(3),then

SoV=0,i.e.,A(1)=0.

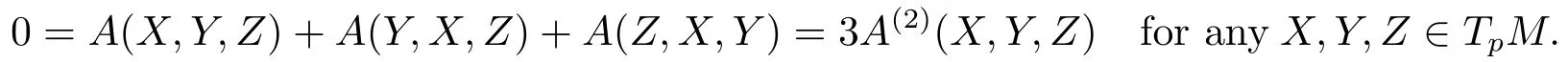
SoA(2)=0 andA(3)=0.

Step 3The three space are orthogonal with each other.

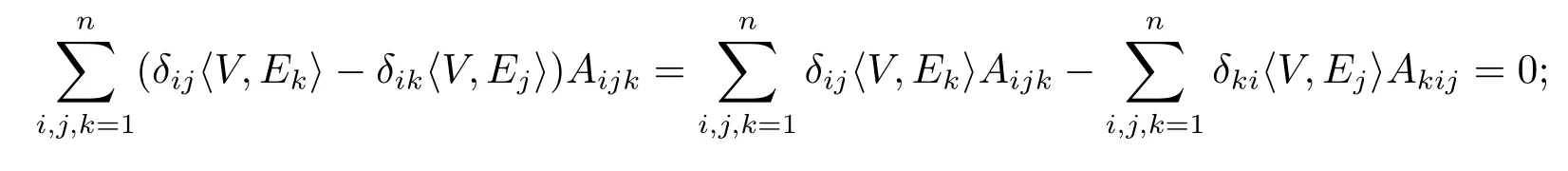
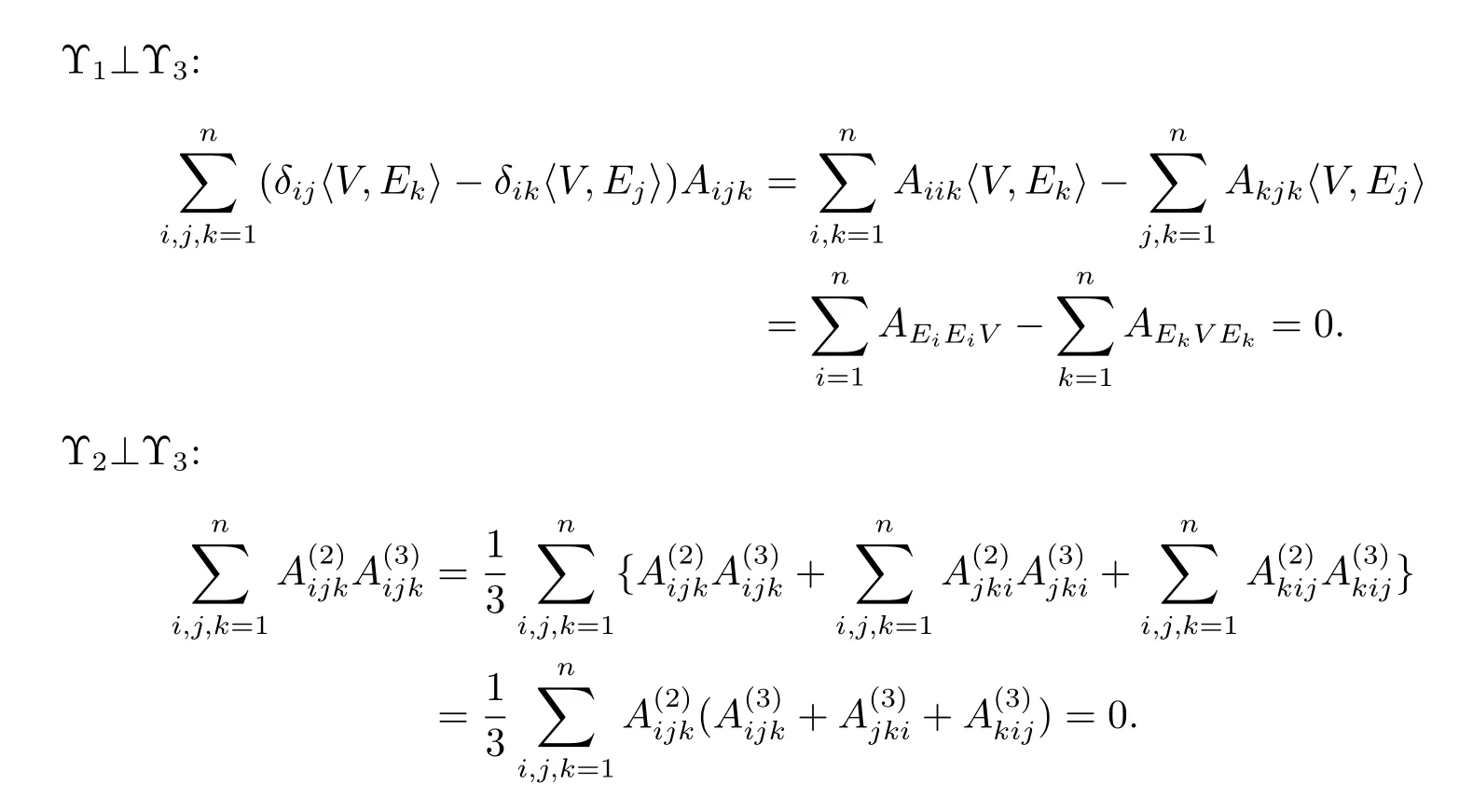
For more about this proof,cf.[12].

The connections whose torsion tensor is contained inare called vectorial.Those whose torsion tensor is in2(TpM)=∧3T?pMare called totally anti-symmetric,and those with torsion tensor in3(TpM)are called of Cartan-type.

We note that any Cartan-type torsion tensorA∈(TpM)is trace-free in any pair of entries,i.e.,for anyZ,one has

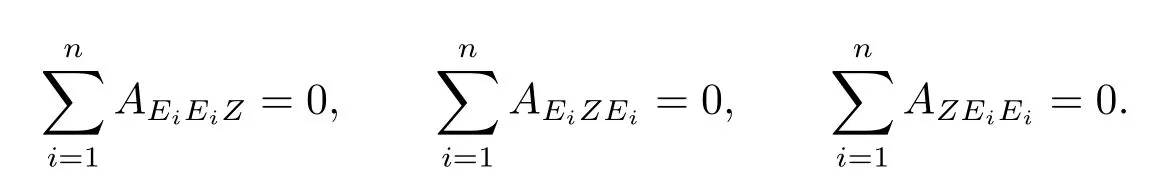
The second equality holds asA∈(TpM),and the third one follows from the cyclic identityAXYZ+AYZX+AZXY=0.

Remark 2.2The invariant quadratic form given in(2.12)has the null space2(TpM)⊕3(TpM).More precisely,one hasA∈2(TpM)⊕3(TpM)if and only ifc12(A)(Z)=0 for anyZ∈TpM.

Remark 2.3The decomposition given in Theorem 2.1 is orthogonal with respect to the bilinear form given in(2.11),i.e.,forα,β∈{ 1,2,3},αβ,andAα∈α(TpM),Aβ∈β(TpM),one gets

Corollary 2.4For any orthogonal connection?′on some Riemannian manifold of dimensionn≥3 there exist a vector fi eldV,a 3-formTand a(0,3)-tensor fi eldSwithSp∈3(TpM)for anyp∈Msuch thattakes the form

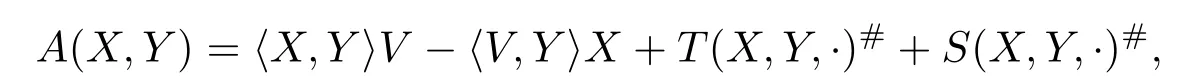
whereT(X,Y,·)#andS(X,Y,·)#are the unique vectors with

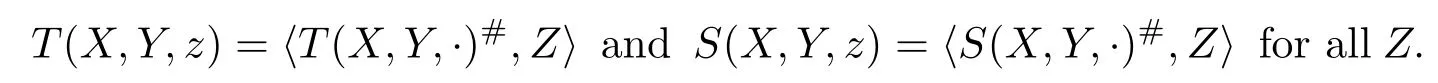
For any orthogonal connection theseV,T,Sare unique.

Lemma 2.5The scalar curvature of an orthogonal connection is given by

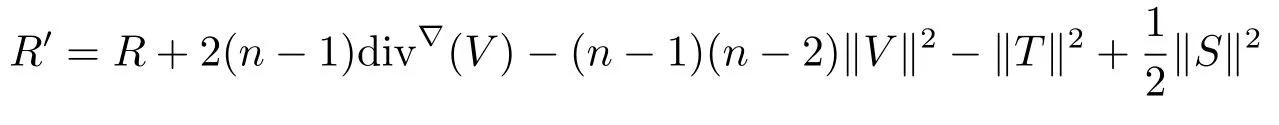
withV,T,Sas in Corollary 2.4,and div?(V)is the divergence of the vector fi eldVtaken with respect to the Levi-Civita connection.

Corollary 2.6LetMbe a closed manifold of dimensionn≥3 with Riemannian metricgand orthogonal connection?′.Let dvol denote the Riemannian volume measure taken with respect tog.Then the Einstein-Cartan-Hilbert functional is

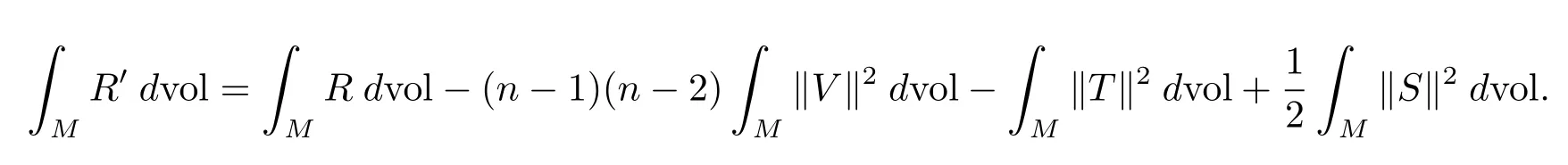
3 The Fundamental Equations under Orthogonal Connections and Some Results

LetMto be a submanifold ofThe signsare orthogonal connection,the Levi-Civita connection,torsion tensor and Riemannian curvature related toM.The signs?′,?,AandRare orthogonal connection,the Levi-Civita connection,torsion tensor and Riemannian curvature related toMinheriting fromand the Riemannian curvature ofM.

We have the two orthogonal decomposition

Under the Levi-Civita connection,we denoteB′byB.

It is easy to check that?′and?′⊥keep compatible with metric,since

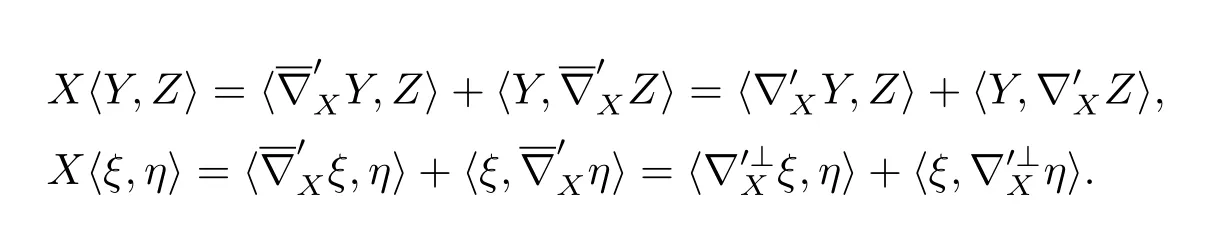
And we have the fact that〈B′(X,Y),ξ〉=〈Aξ(X),Y〉.

Theorem 3.1(Guass Equation)

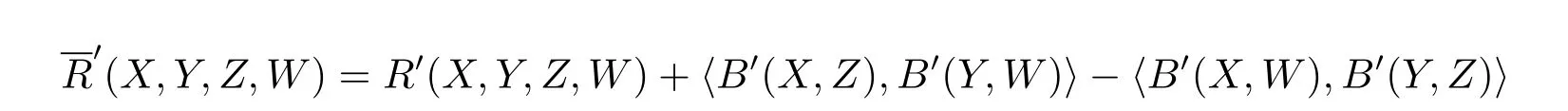
for anyX,Y,Z,W∈TpM.

Proof

Theorem3.2(Codazzi Equation)for anyX,Y,Z∈TpM,which

Proof

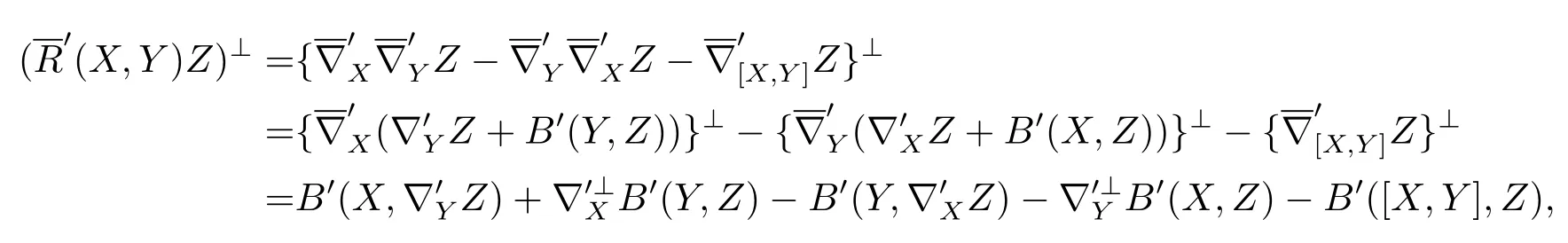
while

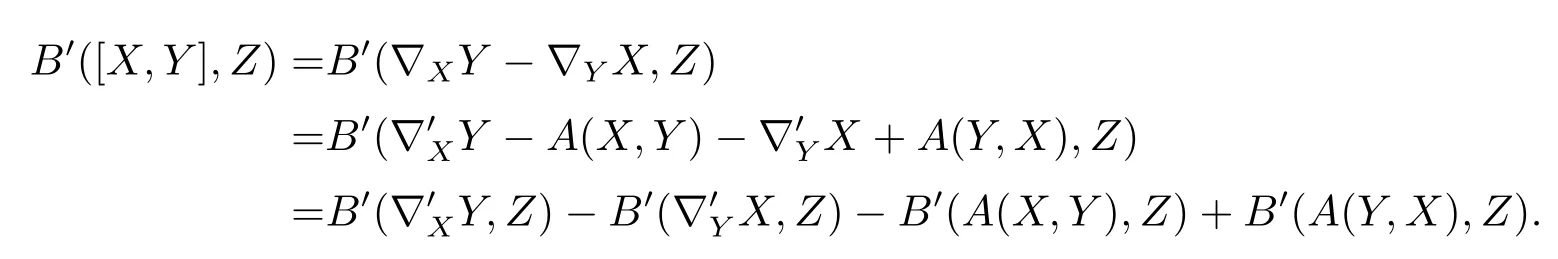
So the equation is found.

Theorem 3.3(Ricci Equation)

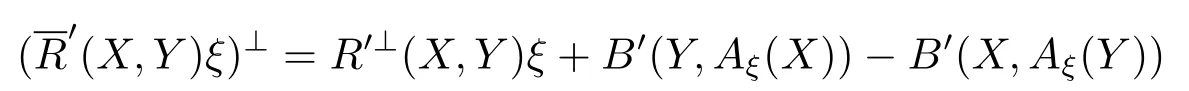
for anyX,

Proof

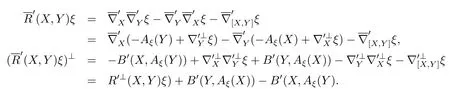
Proposition 3.4If(X,Y)∈TpMfor anyX,Y∈TpM,thenB′(X,Y)=B′(Y,X)=B(X,Y).

Proof

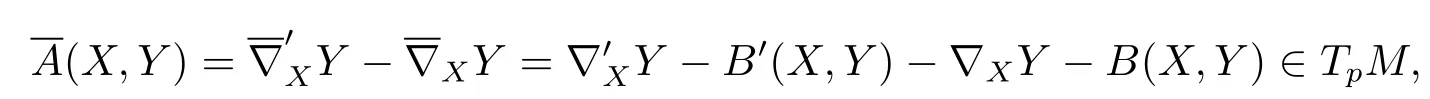
thenB′(X,Y)-B(X,Y)=0,B′(X,Y)=B(X,Y).

De fi nition 3.5We define the mean curvature vector bytrB′.If for anyX∈TM,,we callMis a submanifold with parallel mean curvature vector.

It is easy to check that ifMis a submanifold ofwith parallel mean curvature vector,we have‖H′‖is a constant.Since for any

De fi nition 3.6Mis a submanifold of,then

(1)IfAξ(x)：TxM→TxMsatis fi esAξ(x)=λξ(x)·Id,whichλξ(x)is a constant related to pointx,andIdis identity mapping.Then we call x is a umbilical point related to normal vectorξ.

(2)If for allx∈M,xis a umbilical point related toξ.Then we callMis umbilical related to normal vectorξ.

(3)IfMis umbilical related to any normal vectorξ∈T⊥M.Then we callMis a totally umbilical submanifold.

Proposition 3.7LetMnto be a submanifold ofthenMis a totally umbilical submanifold if and only ifB′(X,Y)=g(X,Y)H′,?X,Y∈TpM.

ProofIfMis a totally umbilical submanifold,then

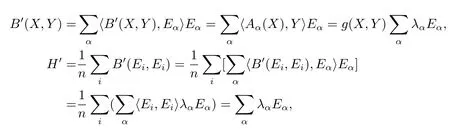
B′(X,Y)=g(X,Y)H′.

IfB′(X,Y)=g(X,Y)H′,?X,Y∈TpM,then?ξ∈T⊥pM,

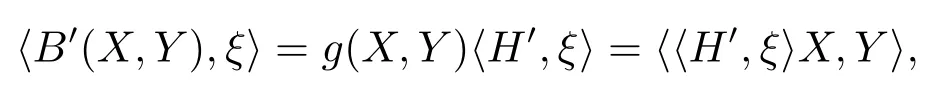
while〈B′(X,Y),ξ〉=〈Aξ(X),Y〉,henceAξ(X)=〈H′,ξ〉X.

Proposition 3.8LetMto be a submanifold of,thenMis a totally geodesic if and only ifMis totally umbilical andH′≡0.

ProofIfB′≡0,then

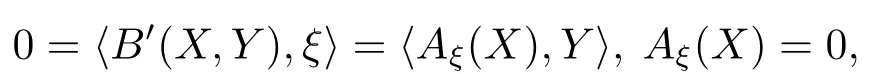
soMis totally umbilical.By Proposition 3.7,B′=gH′,thenH′≡ 0.

IfMis totally umbilical andH′≡ 0,thenB′=gH′=0,soB′≡ 0,Mis a totally geodesic submanifold.

Under the Levi-Civita connections,the Riemannian curvatureRhas the following properties

But under orthogonal connections,(iii),(iv)do not always hold.

We usually denoteG(X,Y,Z,W)〈X,Z〉〈Y,W〉-〈X,W〉〈Y,Z〉.It is easy to check thatGhas the same properties(3.1)asR.

In the rest of this section,we argue Lemma 3.9,Theorem 3.10,Corallary 3.11,and Theorem 3.12 in 3-dimensional Reimannian manifold equipped with an orthogonal connection which torsionTis a totally anti-symmetric satisfyingT=fW1∧W2∧W3(W1,W2,W3is the dual bases ofE1,E2,E3),fis a constant.

Lemma 3.9(M,g)is under the conditions above,then the fi rst Bianchi identity is founded,that is to say

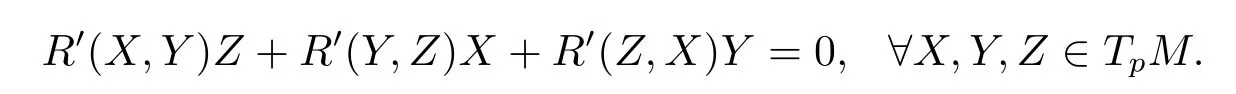
ProofAt any pointp∈M,we choose parallel unit vector fi eldsE1,E2,E3as the bases in the neighborhood ofp.

Since the curvature tensorR′(X,Y)Zat pointpis not related to the extensions ofX|p,Y|p,Z|p,we let the extensions to be

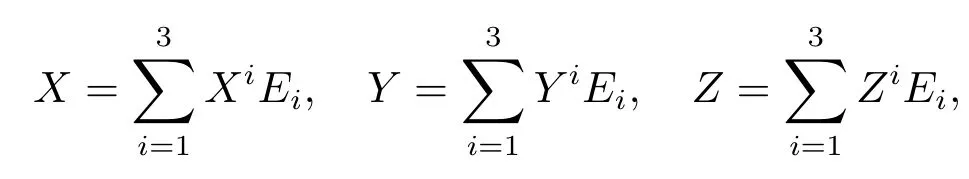
whichXi,Yi,Ziare constants,i=1,2,3,then

Ifi,j,kare at least two identical,

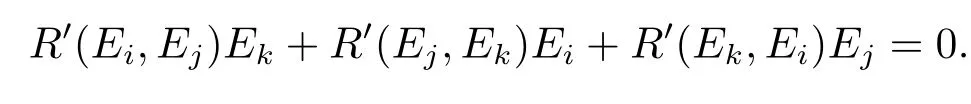
We consideri,j,kare di ff erent from each other,then

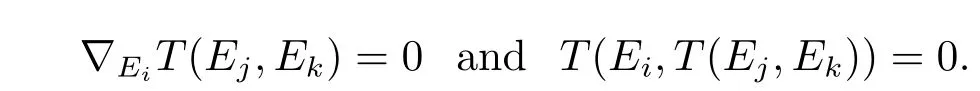
Without of loss generality,we leti=1,j=2,k=3,

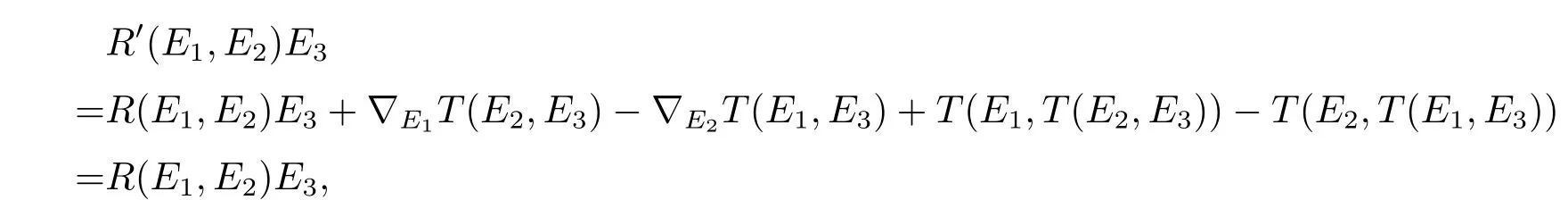
soR′(E1,E2)E3+R′(E2,E3)E1+R′(E3,E1)E2=0.That is to say,in the case ofi,j,kare di ff erent from each other,

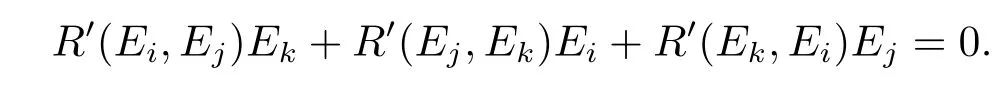
Therefore

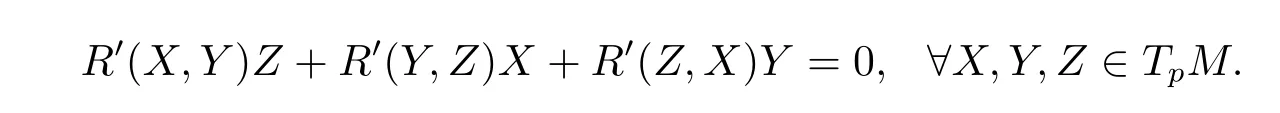
So property(iv)of(3.1)is founded.Since dimM=3,we have?T=0,then

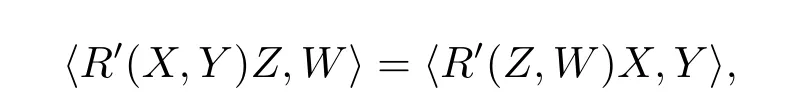
corresponding to the(iii)of(3.1).

After all,(3.1)holds for an orthogonal in 3-dimension under the conditions above.

Theorem 3.10If dimM=3,under an orthogonal connection above,then the curvature tensor ofMat pointpis determined by the all(sections’)sectional curvatures.

ProofBecuase(3.1)holds forR′,we prove the theorem as following.In order to proof the theorem,we only need to prove that if there is another(0,4)-tensor′(X,Y,Z,W)satisfying(3.1),and for any linearly independent vectorsX,Y∈TpM,it always hold that′(X,Y,X,Y)=R′(X,Y,X,Y),then for anyX,Y,Z,W∈TpM,we have′(X,Y,Z,W)=R′(X,Y,Z,W).So letS(X,Y,Z,W)=′(X,Y,Z,W)-R′(X,Y,Z,W),the argument above is equivalent to that if for anyX,Y∈TpM,S(X,Y,X,Y)=0,thenS≡0.Obviously,Sis a(0,4)-tensor satisfying(3.1).ExpandingS(X+Z,Y,X+Z,Y)=0,we have

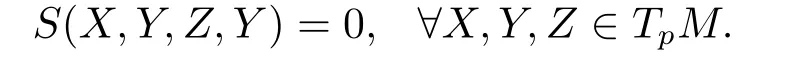
Then expandingS(X,Y+W,Z,Y+W)=0,we have

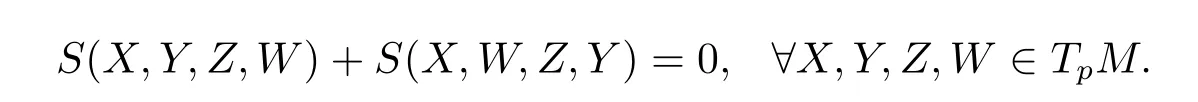
Via(iv)S(X,Y,Z,W)+S(X,Z,W,Y)+S(X,W,Y,Z)=0,we obtain

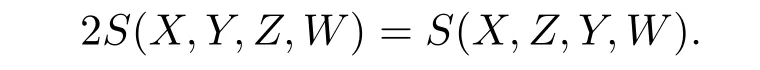
Likewise,

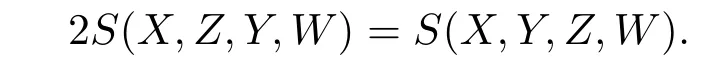
Hence,for anyX,Y,Z,W∈TpM,S(X,Y,Z,W)=0.

Corollary 3.11Let(M,g)a Riemannian manifold,dimM=3,under an orthogonal connection above,thenMis a isotropic manifold if and only if fi xing anyp∈M,

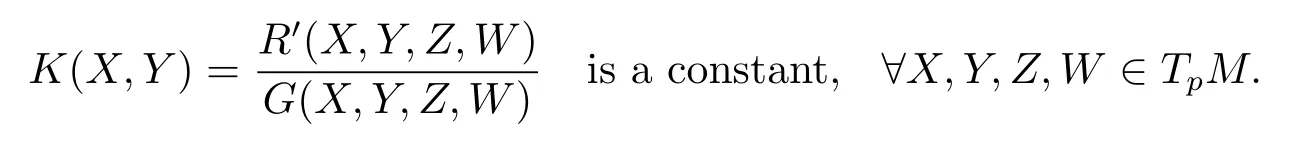
Theorem 3.12is constant curvature Riemannian manifold whichdim=3 and curvature is,equipped with an orthogonal connection above,denoted by (the torsion is).LetMbe a submanifold ofwhich is connected and is totally umbilical,then

(1)Mis a submanifold with a parallel mean curvature vector,andR⊥(X,Y)ξ≡0 under the Levi-Civita connection.

(2)Mis a submanifold of constant curvature,which curvature is

ProofAt fi rst,for convenience,we proof the case ofunder the Levi-Civita connection andn-dimension

Sinceis a constant curvature manifold,then

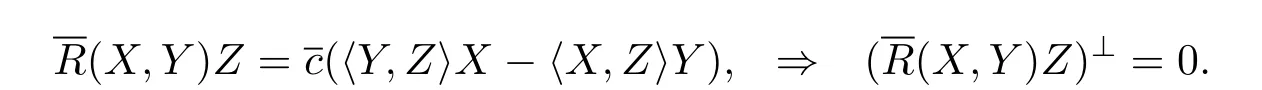
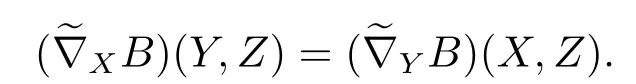
Using Proposition 3.7,B(X,Y)=〈X,Y〉H,we have

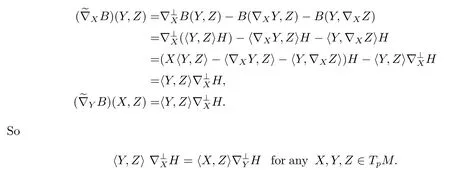
We pickY=Z/=0,X⊥Y,thenfor anyX,Y∈TpM,,i.e.,His parallel related to

Next,proof ofR⊥≡0.

Sinceis constant curvature manifold,then.We have,whileB=B(X,λξY)=λξB(X,Y)=B(Y,Aξ(X)).

(2)Via the Gauss equation,?X,Y,Z,W∈TpM,we have

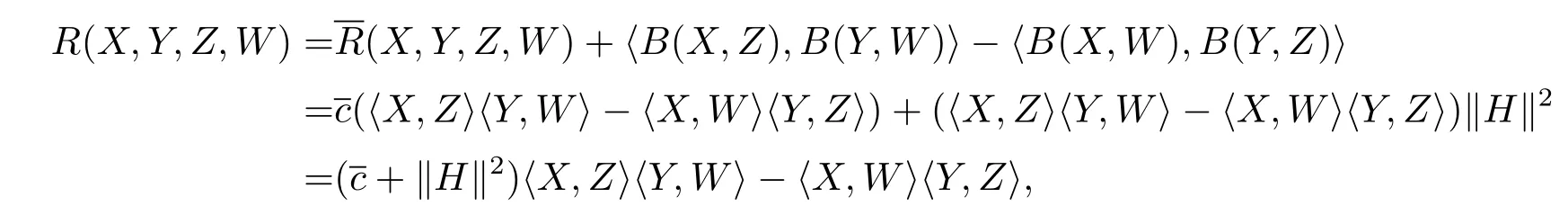
soMis a constant curvature manifold with sectional curvature+‖H‖2,whileis a totally anti-symmetric tensor,Tis also a totally anti-symmetric tensor.Because of dim=3,dimM≤2,T≡0.So the Codazzi equation is the same as the case of the Levi-Civita connection,i.e.,

Combined with Corollary 3.11,we can get the result.

[1]Cartan.Sur les varits connexion a ff ne et la thorie de la rlativit gnralise(premire partie)[J].Ann.Norm.Sup.,1923,40：325-412.

[2]Cartan.Sur les varits connexion a ff ne et la thorie de la rlativit gnralise(premire partie suite)[J].Ann.Norm.Sup.,1924,41：1-25.

[3]Cartan.Sur les varits connexion a ff ne et la thorie de la rlativit gnralise(deuxime partie)[J].Ann.Norm.Sup.,1925,42：17-88.

[4]Agricola I.The Srn lectures on non-integrable geometries with torsion[J].Arch.Math.(Brno),2006,42：5-84.

[5]Tricerri F,Vanhecke L.Homogeneous structures on Riemannian manifolds[M].London Math.Soc.Lecture Note Ser.,Vol.83,Cambridge：Cambridge University Press,1983.

[6]Pfaffle F,Stephan C A.On gravity,torsion and the spectral action principle[J].J.Funct.Anal.,2012,262：1529-1565.

[7]Kobayashi S,Nomizu K.Foundations of di ff erential geometry[M].New York：Interscience Publishers,1969.

[8]Bai Z G,Shen Y B.An introduction to Riemann geometry(revised ed.)[M].Beijing：Higher Edu.Press,2004.

[9]Isaac Chavel.Riemannian geometry,a modern introduction(2nd ed.)[M].Cambridge：Cambridge Cambridge University Press,2006.

[10]Berger M.Quelques formules de variation pour une structure riemannienne[J].Ann.Norm.Sup.,1970,3(4)：285-294.

[11]Tricerri F,Vanhecke L.Homogeneous structures on Riemannian manifolds[M].London Math.Soc.,Lecture Note Ser.,Vol.83 Cambridge：Cambridge University Press,1983.

[12]Nie Zhi.On the Guass equation and Chern connections of Finsler submanifolds[J].J.Math.,2004,24(5)：537-542.

黎曼流形在正交聯(lián)絡(luò)下的全臍點子流形

李凱鵬,王旭升

(武漢大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,湖北武漢 430072)

本文研究了正交聯(lián)絡(luò)下子流形基本方程以及在全臍點子流形中的應(yīng)用.利用Cartan的方法將撓率張量分解成三個部分,計算得到正交聯(lián)絡(luò)下的三個基本方程,并考慮一個特殊的正交聯(lián)絡(luò),證明了其黎曼曲率會有類似于Levi-Civita聯(lián)絡(luò)下的性質(zhì).利用基本方程得到常曲率空間中的全臍點子流形的性質(zhì),推廣了Levi-Civita聯(lián)絡(luò)下的相應(yīng)結(jié)果.

正交聯(lián)絡(luò);黎曼流形的基本方程;子流形;臍點

O186.12

on：53C05;53C17

A Article ID： 0255-7797(2017)04-0672-13

date：2017-01-10Accepted date：2017-03-27

Supported by National Natural Science Foundation of China(11571259).

Biography：Li Kaipeng(1989-),male,born at Fuzhou,Fujian,postguaduate,major in di ff erential geometry and geometric analysis.