鮑春梅,李書海,馬麗娜

(赤峰學院數(shù)學與統(tǒng)計學院,內蒙古赤峰 024000)

一類λ-對數(shù)Bazilevic函數(shù)的Fekete-Szeg¨o不等式

鮑春梅,李書海,馬麗娜

(赤峰學院數(shù)學與統(tǒng)計學院,內蒙古赤峰 024000)

本文研究了一類λ-對數(shù)Bazilevic函數(shù)的Fekete-Szeg不等式.利用分類討論的方法獲得了的精確估計,推廣了一些已有的相關結果.

解析函數(shù);λ-對數(shù)Bazilevic函數(shù);從屬于;Fekete-Szeg不等式

1 引言

設S表示單位圓盤E={z：|z|＜1}內形如的單葉解析函數(shù)類的全體.S?,C和K分別表示通常的星像函數(shù)類,凸函數(shù)類和近于凸函數(shù)類,它們都是S的子類.

設f(z)與g(z)在E內解析,若存在E內滿足|φ(z)|≤|z|的解析函數(shù)φ(z)(不必單葉),使得f(z)=g(φ(z)),則稱f(z)從屬于g(z),記為f(z)?g(z).

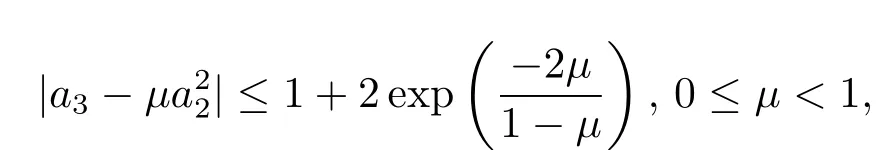
且對任意的μ∈[0,1),等號均能成立.

在文獻[2-8]中分別研究了某些星像函數(shù)類和近于凸函數(shù)類的Fekete-Szeg不等式.本文引進一類λ-對數(shù)Bazilevic函數(shù),討論該函數(shù)類的Fekete-Szeg不等式,并得到對應的極值函數(shù).

定義設λ≥0,α≥0,-1≤B＜A≤1,若存在g(z)∈S?,使得f(z)∈S,且滿足條件

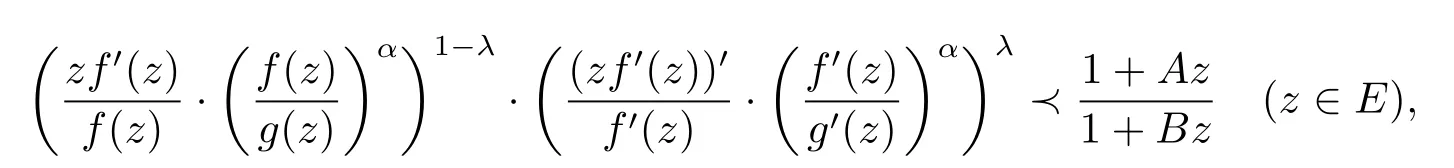
則稱f(z)為λ-對數(shù)Bazilevic函數(shù),這類函數(shù)記為L(λ,α,A,B),其中的冪函數(shù)取主值.

下面對函數(shù)類L(λ,α,A,B)中建立Fekete-Szeg不等式,為此需要如下引理.

引理1[9]設φ(z)=d1z+d2z2+···在E內解析且滿足|φ(z)|＜|z|,則

引理2[10]設p(z)=1+p1z+p2z2+···在E內解析且對任意z∈E,滿足Rep(z)＞0,則

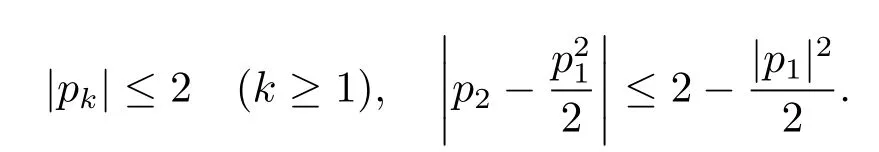
2 主要結果及證明

定理設λ≥0,α＞1,-1≤B＜A≤1,若∈L(λ,α,A,B),則對任意實數(shù)μ,有

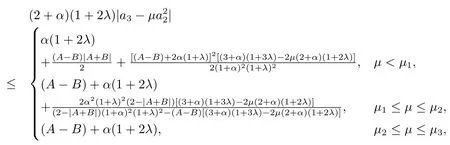
其中

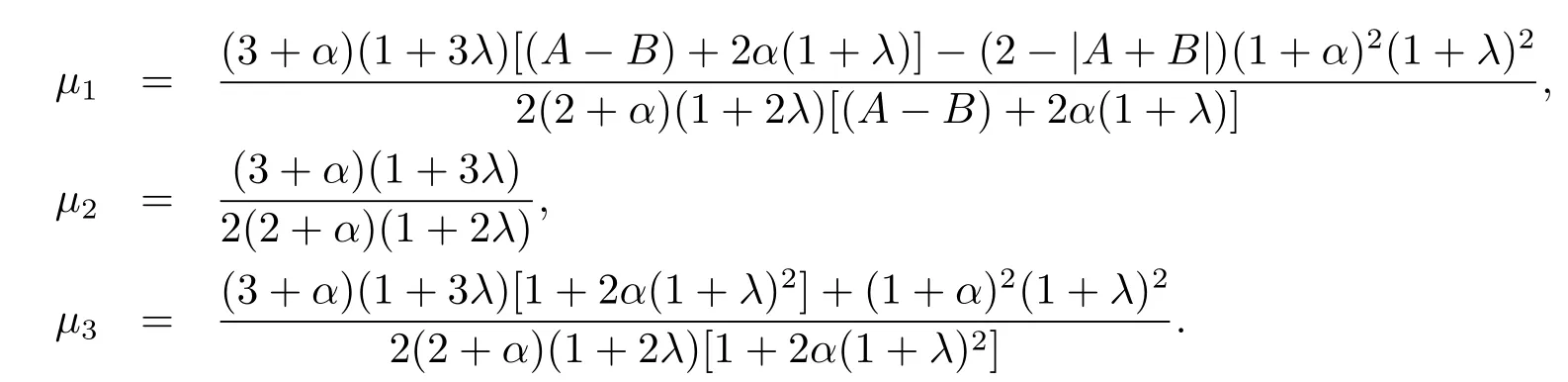
證因為f(z)∈L(λ,α,A,B),所以存在g(z)=z+b2z2+b3z3+···∈S?和E內滿足條件 |φ(z)|≤|z|的解析函數(shù)φ(z)=d1z+d2z2+···,使得

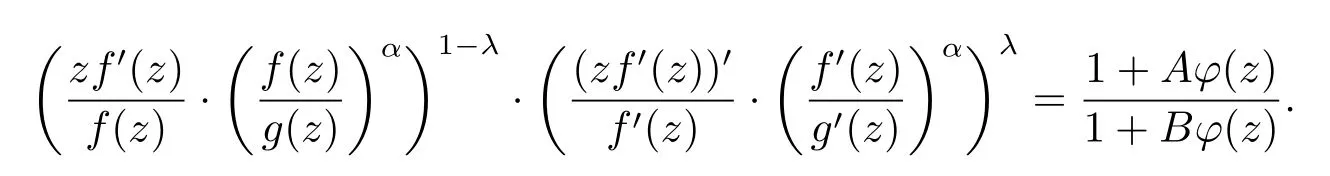
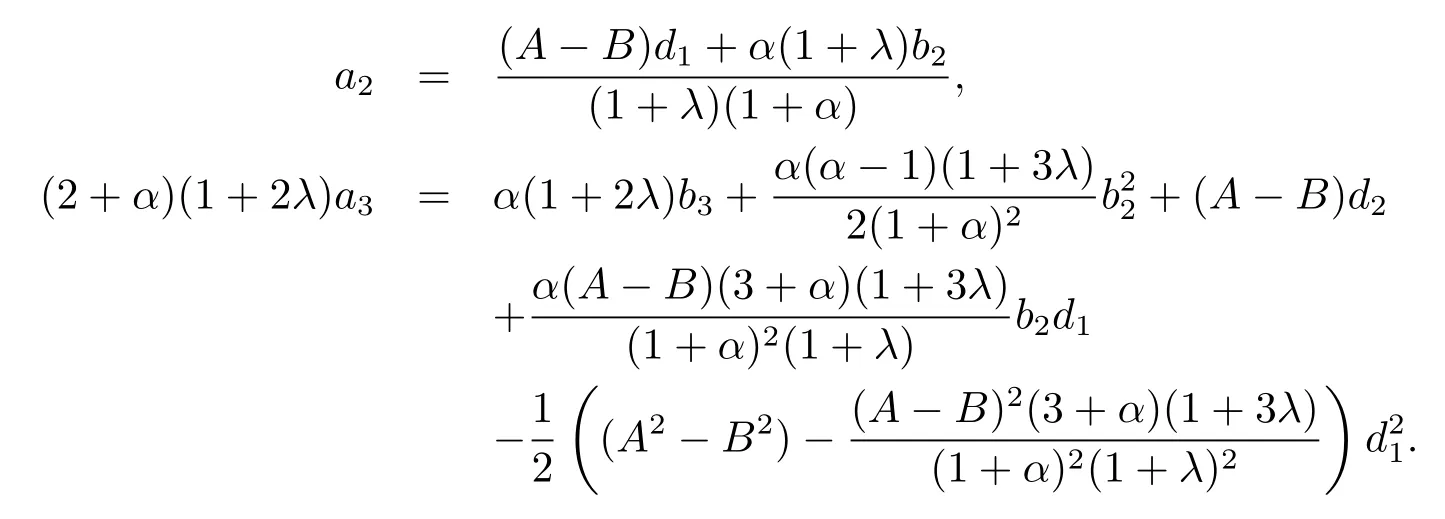
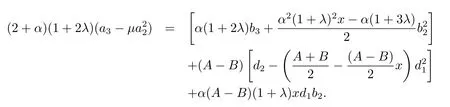
因為

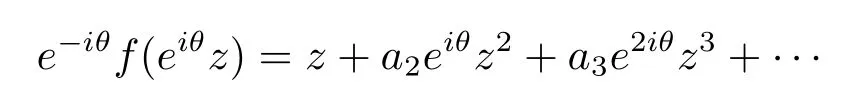
仍屬于L(λ,α,A,B),所以不失一般性,可以假定.下面估計.

由于g(z)∈S?,所以存在E內具有正實部的解析函數(shù)p(z)=1+p1z+p2z2+···,使得zg′(z)=g(z)p(z),比較系數(shù)可得

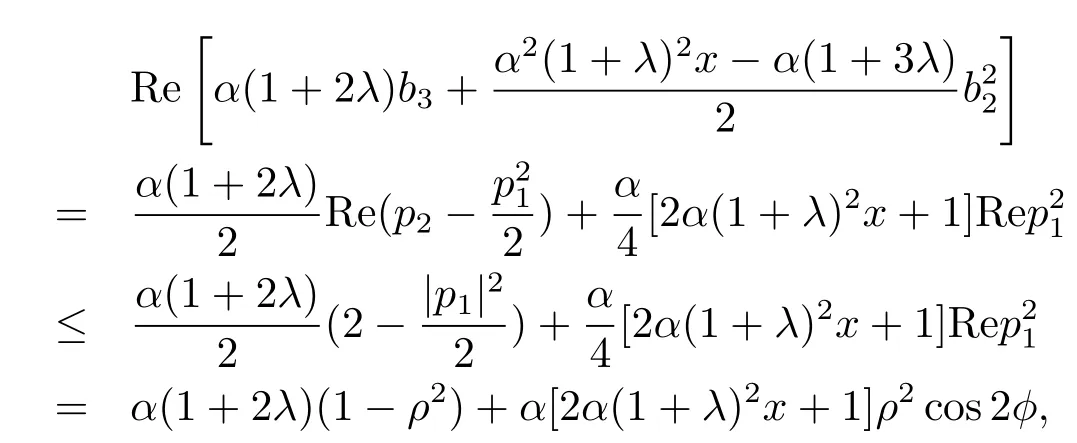
其中b2=p1=2ρeiφ,0≤ρ≤1.

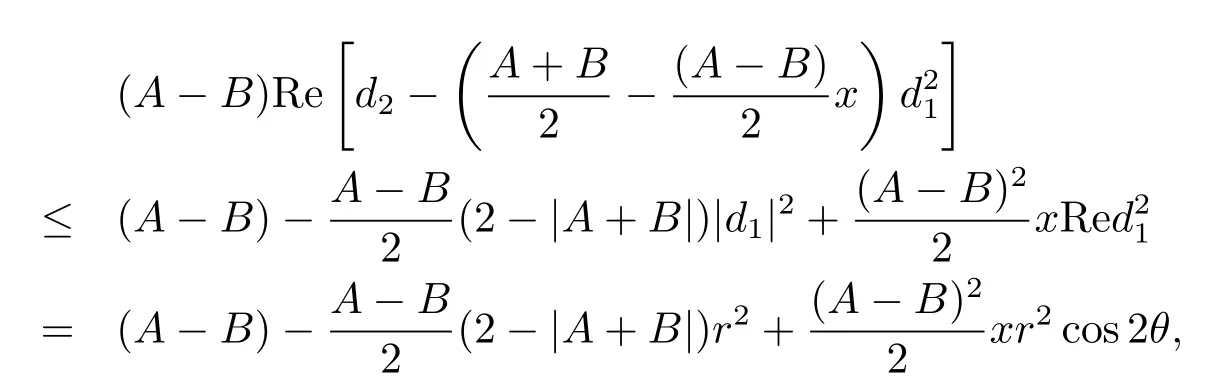
其中d1=reiθ,0≤r≤1.所以

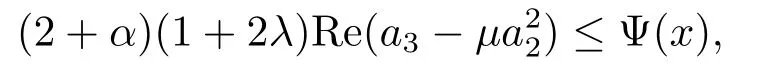
其中

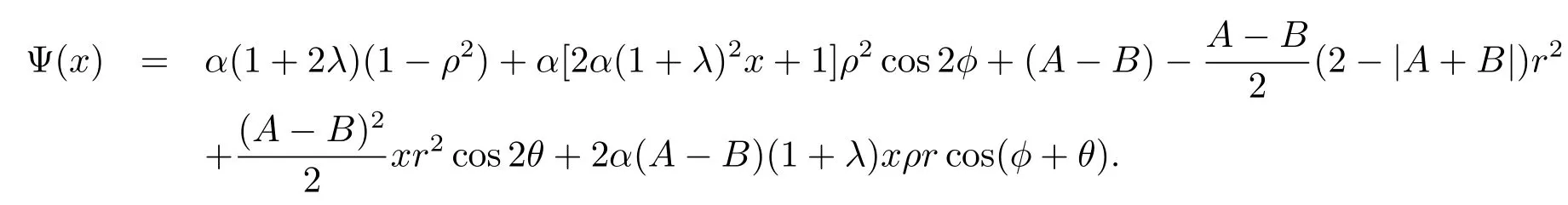
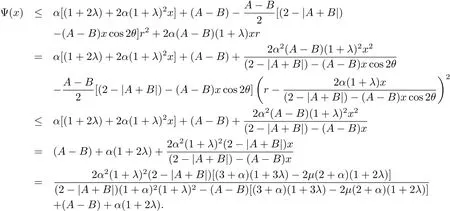
當μ1≤μ≤μ2時,不存在對應的極值函數(shù).

當μ≤μ1時,不存在對應的極值函數(shù).

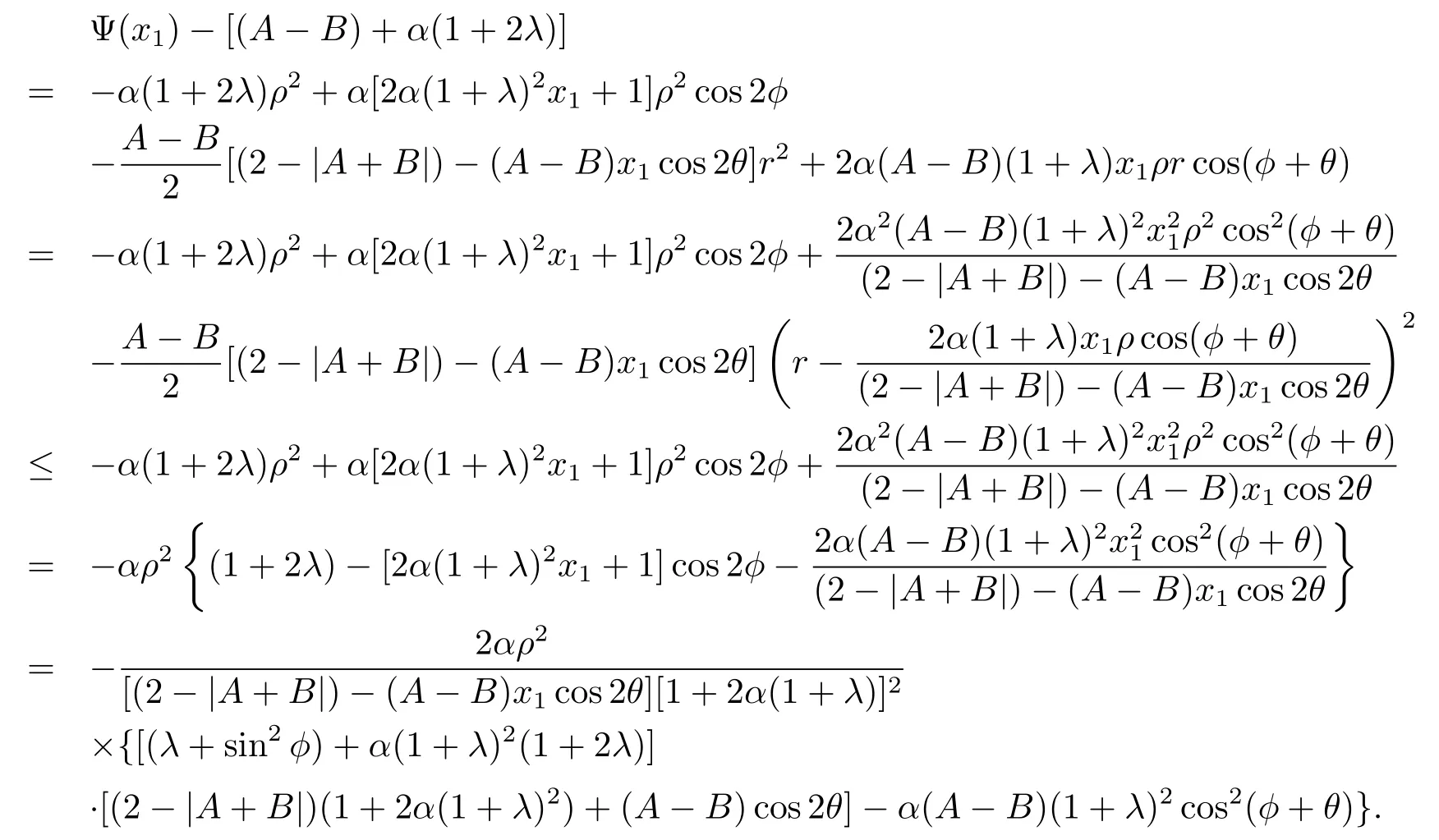
令

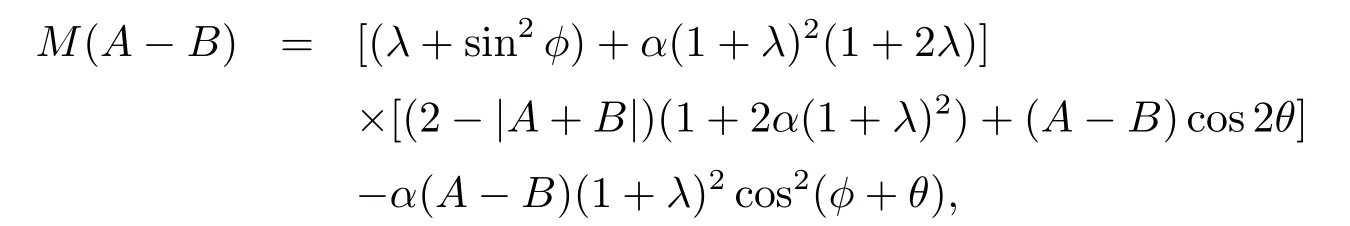
則M(A-B)是A-B的一次函數(shù),且

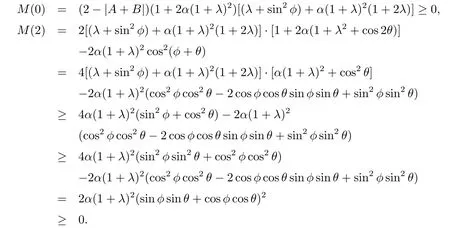
故當0＜A-B＜2時,M(A-B)≥0,從而(x1)≤(A-B)+α(1+2λ).對于0≤t≤1,有

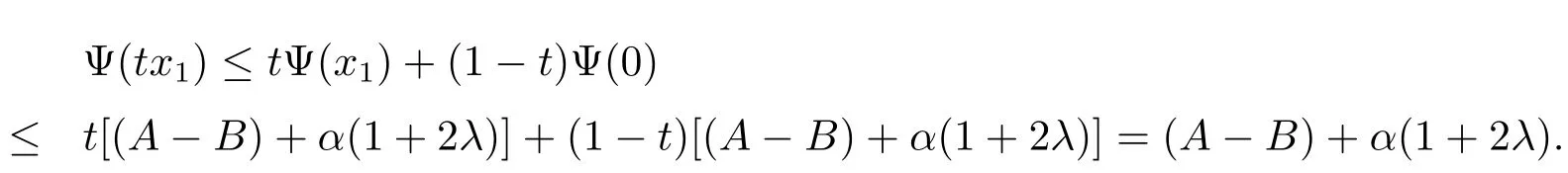
當b2=0,b3=1,d1=0,d2=1時等號成立.對應的極值函數(shù)為

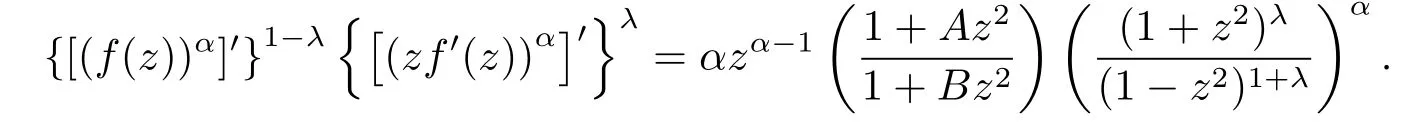
綜上所述,本定理得證.

[1]Fekete M,SzegG.Eine Bermaerkung uber ungerade schlichte functions[J].London Math.Soc.,1933,8：85-89.

[2]劉名生.強擬星函數(shù)的Fekete-Szeg不等式[J].數(shù)學研究與評論,2000,20(4)：591-595.

[3]London R R.Inequalities for close-to-convex functions[J].Proc.Amer.Math.Soc.,1993,117(4)：947-950.

[4]鮑春梅,李書海.一類β級擴展的Bazilevic函數(shù)及其Fekete-Szeg問題[J].華南師范大學學報(自然科學版),2010(3)：7-10.

[5]Gao Chunyi.Fekete-Szegproblem for strongly Bazilevic functions[J].Northeast Math.,1996,12(4)：469-474.

[6]張洪光,李書海.關于Bazilevic函數(shù)族的一個擴展及其Fekete-Szeg問題[J].純粹數(shù)學與應用數(shù)學學報,2008,24(1)：167-173.

[7]崔志峰,劉名生.用卷積定義的解析函數(shù)子類的Fekete-Szeg不等式[J].數(shù)學雜志,2011,31(5)：955-961.

[8]劉名生.Bazilevic函數(shù)類的子類的性質[J].數(shù)學雜志,2001,21(1)：33-37.

[9]夏道明,張開明.從屬函數(shù)的一些不等式[J].數(shù)學學報,1958,8(3)：408-412.

[10]Pommerenke C H(楊維奇譯).單葉函數(shù)[M].北京：科學出版社,1987.

BAO Chun-mei,LI Shu-hai,MA Li-na
(School of Mathematics and Statistics,Chifeng University,Chifeng 024000,China)

In this paper,we discuss the Fekete-Szeginequality of a class ofλ-logarithmic Bazilevic function.Using the methods of the classi fi cation,we obtain the accurate estimation of,which generalizes some known results.

analytic function;λ-logarithmic Bazilevic function;subordinate;Fekete-Szeginequality

on：30C45

O174.51

A

0255-7797(2017)04-0845-06

2015-05-04接收日期：2015-08-06

內蒙古自治區(qū)自然科學基金資助(2014MS0101).

鮑春梅(1962-),女,蒙古族,內蒙古赤峰,教授,主要研究方向：復分析及其應用.