Hu Mi,Xia Yonghui(Schoolof Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)

Periodic solutions ofa neutralimpulsive differential equation

Hu Mi,Xia Yonghui?
(Schoolof Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)

In this paper,we considera neutralimpulsive differentialequation.An impulsive predatorprey model with non-monotonic functionalresponse is investigated.Some novelsufficient conditions are obtained for the nonexistence of periodic solutions and the global existence of at least one or two positive periodic solutions.Ourmethod is based on Mawhin′s coincidence degree and novelestimation techniques for the priori bounds of unknown solutions.An application is presented to illustrate the feasibility and effectiveness of our main results.

predator-prey model;periodic solution;neutral;impulsive

2010 MSC:34K23,34D30,37C60,37C55,39A12

1 Introduction

The predator-prey modelplays a greatrole in the mathematicalecology.According to the functionalresponse ofpredatorto prey density and its differentrole in modeling,Holling[1]proposed three types ofmonotonic functionalresponses g(x)=xand a nonmonotonic response,so-called Holling type IV functionalresponseg(x)=.The multiple bifurcationsofa predator-prey system with anotherkind ofnonmonotonic functionalresponse g(x)=x e?βxwere investigated by Xiao and Ruan[2].

To incorporate the periodicity ofthe environment(e.g.food supplies,seasonaleffects ofweather,mating habits, etc.)in many biologicaland ecologicaldynamic systems,itis necessary to consider periodicity of the parameters in the models.For examples,the authors of[3–5]have considered the predator-prey modelwith Holling type IV functionalresponse by assuming a periodic environment.Recently,Xing and Xia[6]studied the nonexistence of periodic solutions and the globalexistence of atleastone or two periodic solutions of the following system with a generalnonmonotonic response:

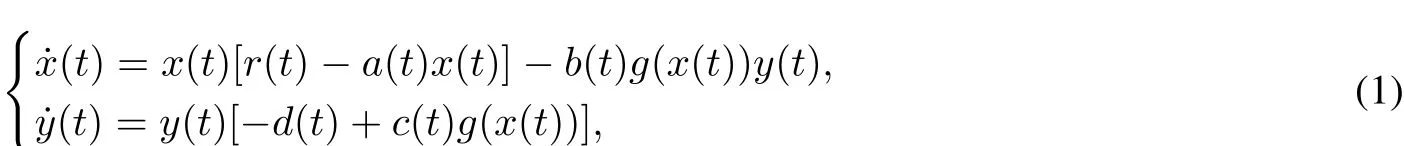
where g(x(t))is the function response,it is assumed that g:[0,∞)→[0,∞)is continuous and satisfies the non-monotonic condition:

(1)g(0)=0;

(2)there exists a constant M＞0,such that(x?M)g′(x)＜0 for x/=M.

Itis easy to see that g is increasing on[0,M),decreasing on[M,∞)and g(x)≤g(M)for x≥0.Forexamples

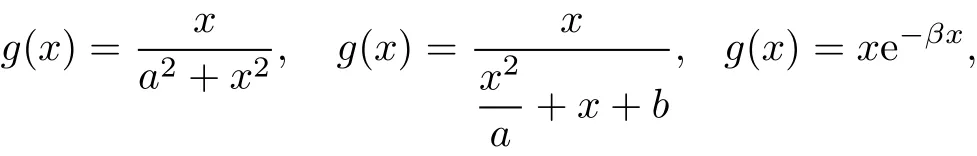
where M,β,a,b are constants.However,there is no published paperconsidering the neutralimpulsive system with nonmonotonic responses.Motivated by[4,7–8],in this paper,we will consider a neutral delayed predator-prey system

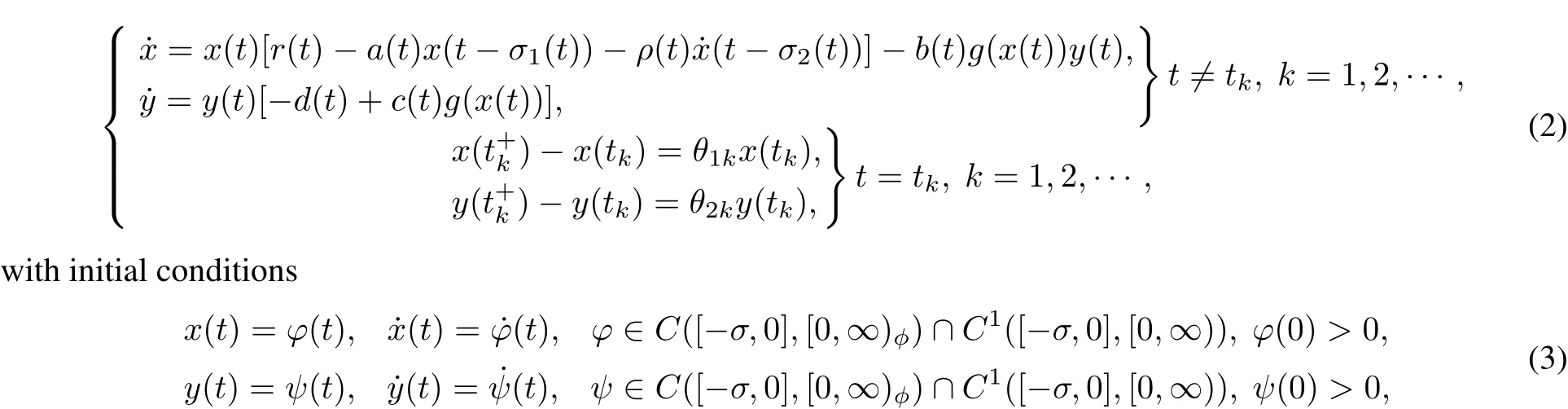
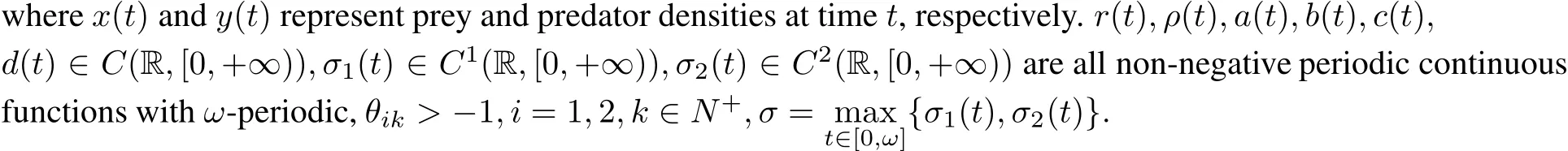
The purpose of this paper is to obtain new sufficientconditions for the nonexistence of periodic solutions and the global existence of at least one or two positive periodic solutions.It should be noted that the method to obtain the globalexistence of atleastone or two positive periodic solutions is much differentfrom the previous work[6]due to the introduction of the neutralterm˙(t?σ2(t))in system(2).As usual in,to obtain the priori bounds of unknown solutions to the operatorequation Lz=λNz,we need boundness of|p˙(t)|d t.If we were to use the same ideas in[6],itis easy to obtain that

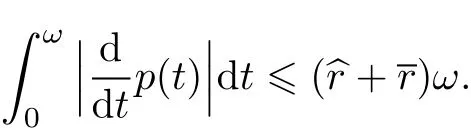
However,due to the neutraltermx˙(t?σ2(t)),itshould be

On the rightside of(5),there is a term(t?σ2(t))|d t.So how to dealwith this term,this is a difficulty we should overcome.The method used in the previous work[6]does notwork.Thus,some novelarguments should be employed.To see how this problem is handled,the readercan refer to(16)–(29)in Section.

2 Preliminaries

With the assumption(H1)and(H2),we considerthe following system:

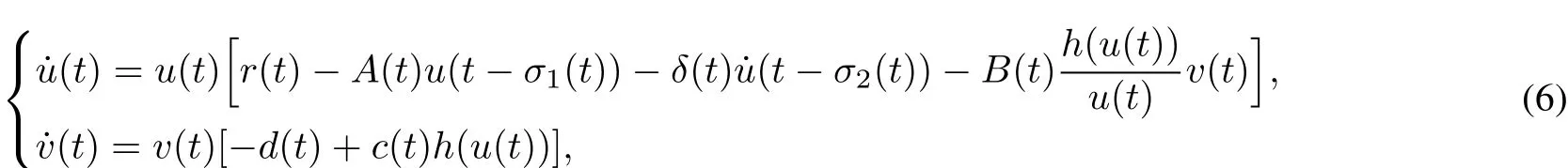
with the initialconditions

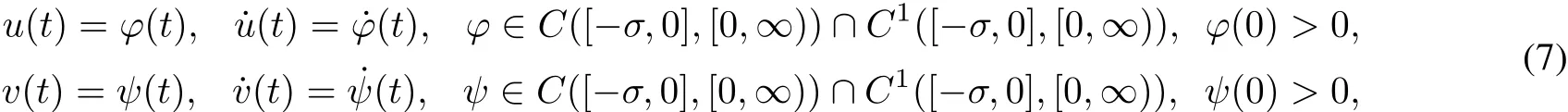
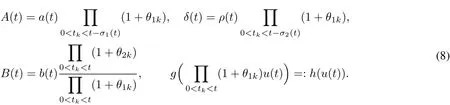
where Lemma 1 Assume that(H1)and(H2)are satisfied,then we have

(i)if(u(t),v(t))Tis a solution of system(6)with initialcondition(7),then(x(t),y(t))Tis a solution of systems (2)with initialcondition(3),where

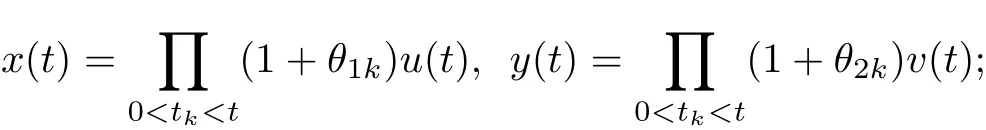
(ii)if(x(t),y(t))Tis a solution of systems(2)with initialcondition(3),then(u(t),v(t))Tis a solution of systems (6)with initialcondition(7),where

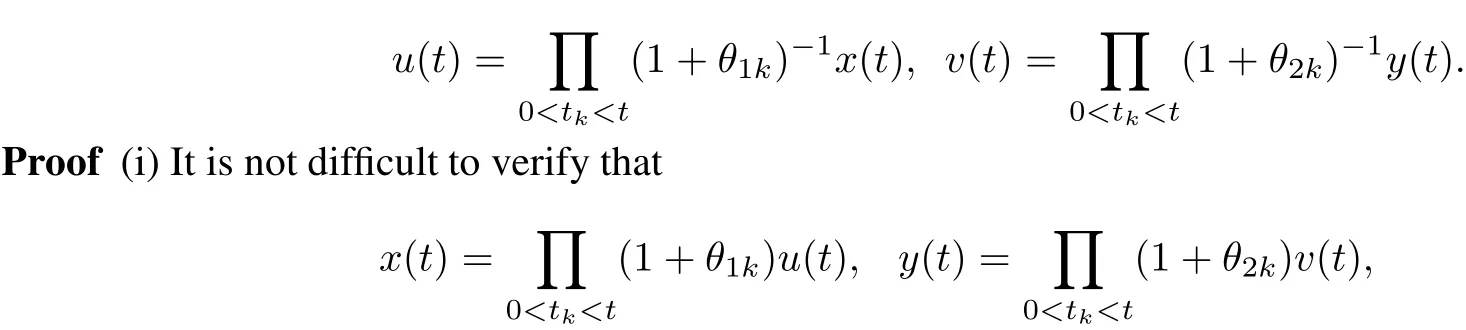
are absolutely continuouson each interval(tk,tk+1].Forany t/=tk,k∈N+,we have

Thus,we obtain

The above equalities imply that u(t)and v(t)are continuouson[?σ,∞).Itis easy to see that u(t)and v(t)are absolutely continuouson[?σ,∞).Similary,we can prove that are solutions ofsystem(6).

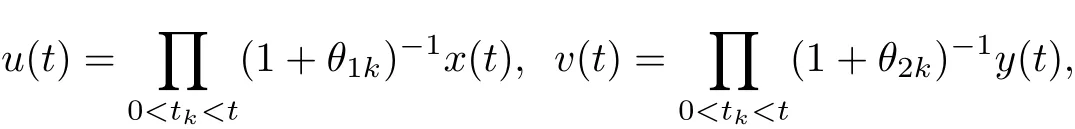
From Lemma 1,we see thatif we wantto prove the existence of positive periodic solutions of system(2),itis sufficientto prove the existence of positive periodic solutions of system(6).

3 Nonexistence

Firstly,we shall give a necessary conditionfor the existence of periodic positive solutions of system(2)with initial condition(3).Notice that h(u(t))Thus,there exists M such that h(M)= max h(u)=max g(x)=g(M).

Theorem 1 Ifsystems(2)and(3)have a positiveω-periodic solution,then h(M)≥D.

Proof Make the change ofvariables

Thus,system(6)is equivalentto system(12)on.Assume thatsystem(12)hasω-periodic solution(p(t),q(t))T, i.e.,p(t+ω)=p(t),q(t+ω)=q(t).Integrating the second equation of(12)on the interval[0,ω],we have

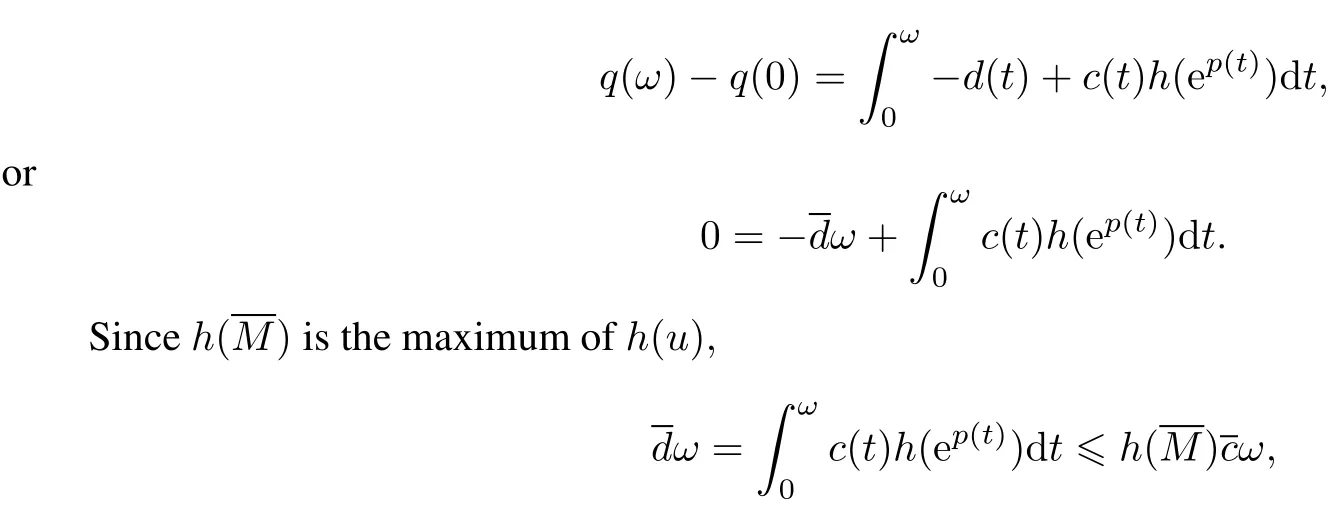
We complete the proofof Theorem 1.And we see the following theorem immediately.

Theorem 2 If h(M)＜D,then systems(2)and(3)have no positiveω-periodic solution.

4 Existence of one periodic solution

In this section,to guarantee the globalexistence of atleast one positive periodic solution,we introduce the continuation theorem of Mawhin′s coincidence degree theory from Gaines and Mawhin[9].

Let X,Y be two realnormed vectorspaces,L:Dom L?X→Y be a linearmapping,and N:X→Y be a continuous mapping.We callthe mapping L a Fredholm mapping ofindex zero if dim Ker L=codim Im L＜∞and Im L is closed in Y.If L is a Fredholm mapping ofindex zero,there existcontinuous projections P:X→X,and Q:Y→Y such thatIm P=ker L,Ker Q=Im L=Im(I?Q),then L|DomL∩KerP:(I?P)X→Im L is invertible.We denote the inverse ofthis map by Kp.Assume?X is an open set,we say thatthe mapping N is L-compacton,if QN()is bounded and Kp(I?Q)N:→X is compact.As Im Q is isomorphic to Ker L,there exists an isomorphism J:Im Q→Ker L.

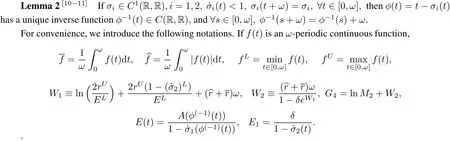
Lemma 3(Continuation theorem[9])Let L be a Fredholm mapping of index zero and N be L-compacton ?.Assume

(a)for everyλ∈(0,1),inequality Lz/=λNz implies z∈??;

(b)QNz/=0 for each z∈??∩Ker L and deg{JQN,?∩Ker L,0}/=0.

Then,the operatorequation Lz=has atleastone solution in Dom L∩

Theorem 3 In addition to(H1)and(H2),furthersuppose that

(H3)h(M)=D;

Then,system(6)with initialvalue condition(7)has atleastone positiveω-periodic solution.

Proof Take

is closed in Y.P and Q are continuousprojectorssatisfy

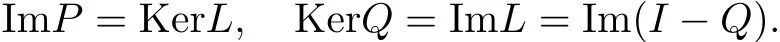
Then,L is a Fredholm operatorof index zero,and ithas a unique inverse Kp:Im L→Dom L∩Ker P,

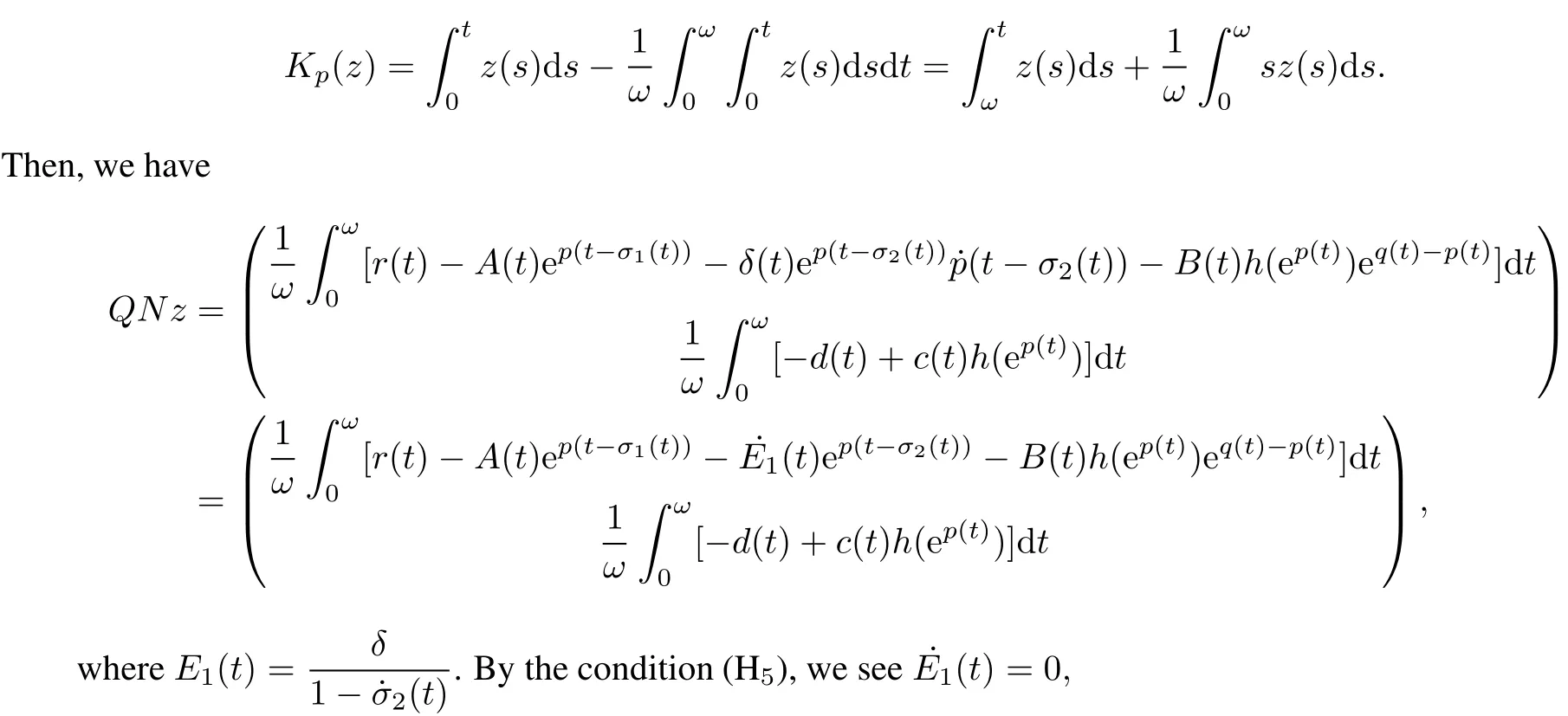
Obviously,QN and Kp(I?Q)N are both continuous.Using the Arzela-Ascolitheorem,itis notdifficultto prove that Kp(I?Q)N()is a compact operator and QN(?)is bounded for any open set??X.Thus,for any open bounded set??X,N∈?is L-compact.

Now we need to find an appropriate open bounded subset?in orderto apply Lemma 3.Corresponding to the operatorequation Lz=λNz,λ∈(0,1),we have the following system

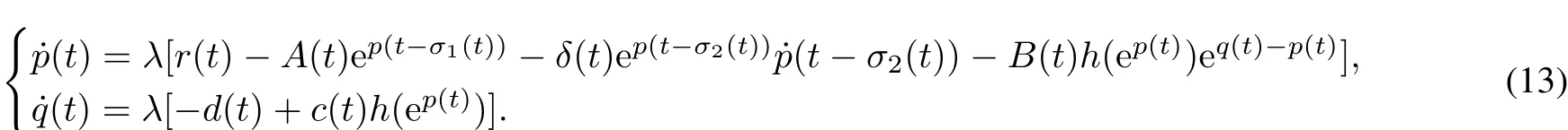
Assume thatsystem(13)has a solution(p(t),q(t))T∈X fora certainλ∈(0,1).An integration of system(13) over[0,ω]leads to

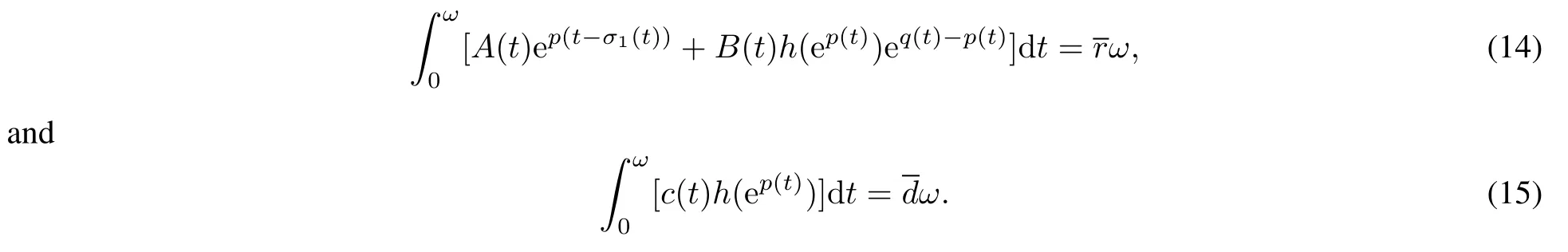
Therefore,we have

Similarly,from the second equation of(13),and(15),we get

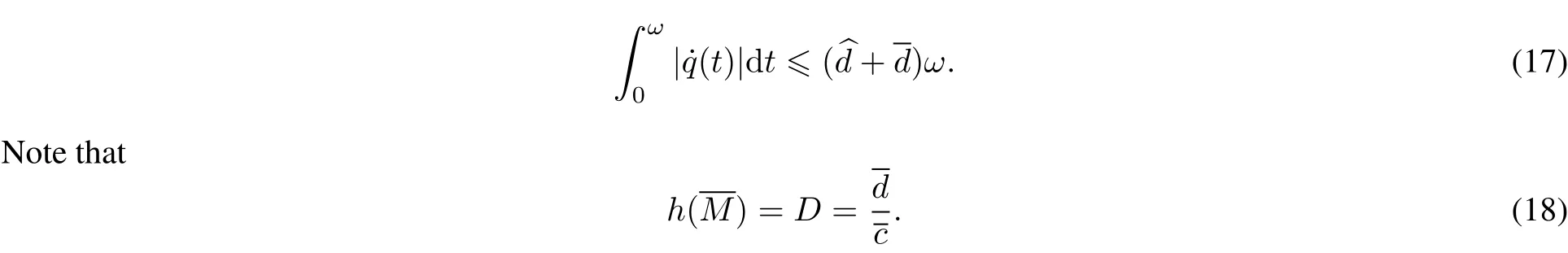
Then,there existsξ1∈[0,ω]such that

Let t?σ1=s.By Lemma 2 and(14),we have

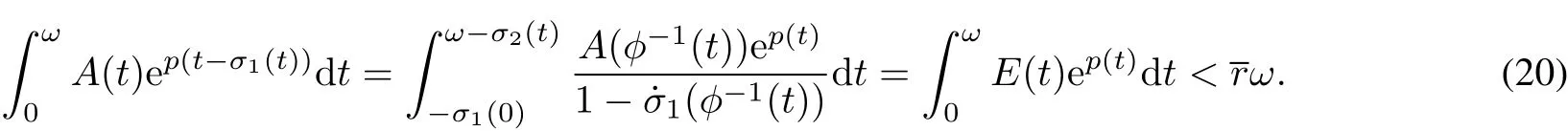
By the mean value theorem in calculus,there exists a numberξ2∈[0,ω]such that

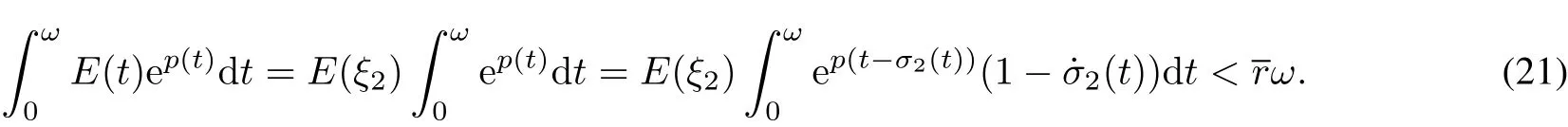
Forsome numberξ3∈[0,ω]such that

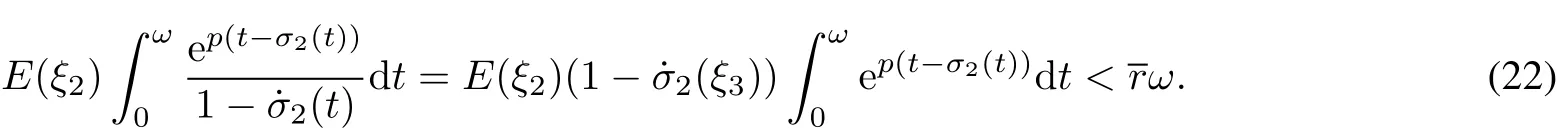
Then,for someξ∈[0,ω],

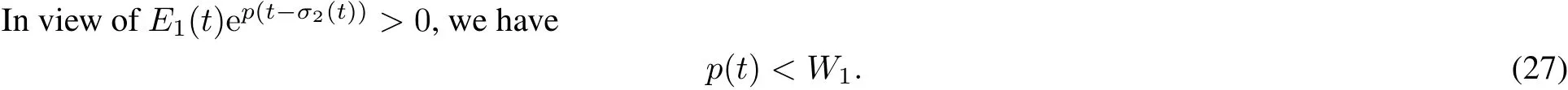
From(13),(14),(16)and(27),we have

In view of(H4)1?δeW1＞0,we have

Combining this with(17),(27),(30)and(31),we have

Itis easy to see that?satisfies the condition of Lemma 3.When z=(p,q)T∈??∩Ker L=??∩R2,z is a constantvectorin R2with‖z‖=W+W+C and we have QNz/=0.Moreover,we define the homomorphism J: Im Q→Ker L,the identity mapping.By the assumption in Theorem 3,itis easy to prove that

where deg(·)is the Brouwer degree[9].Now,we have proved that?satisfies allthe requirements of Lemma 3.It follows that Lz=Nz has atleastone solution in Dom L∩?.

5 Existence of two periodic solution

In this section,we considersystem(12)underthe assumption h(M)＞D.From the non-monotonic condition, if h(M)＞D,then the equation h(M)=D has two positive solutions M1and M2such that

Theorem 4 In addition to(H1)and(H2),we further suppose that

Then,system(6)has atleasttwo positiveω-periodic solutions.

Proof In order to prove that system(2)has two positiveω-periodic solutions,the most important task is to search for at least two appropriate open bounded subsets?1,?2in X for the application of Lemma 3.Let X,Y,L,N,P,Q be defined as in the proofof Theorem 3,and let z=(p(t),q(t))T∈X be a solution of Lz=λNz fora certainλ∈(0,1).

Since(p(t),q(t))T∈X,there existη?,η?∈[0,ω]such that

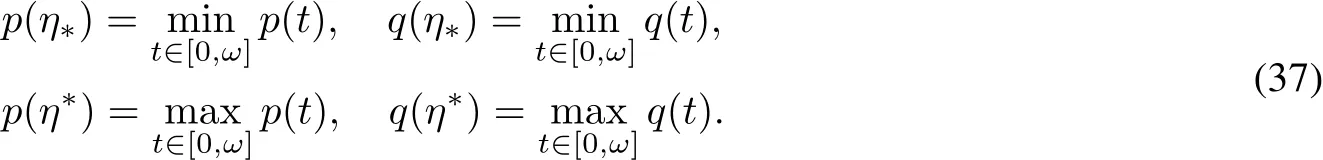
We claim that p(t)/=ln M,t∈[0,ω].Otherwise,itimplies that h(M)=D,which contradicts(H6).Therefore, either p(t)∈(?∞,ln)or p(t)∈(ln,∞).

Case 1:p(t)＜ln M,t∈[0,ω].From(14),(H6)and the non-monotonic condition,there existsθ1∈[0,ω] such that

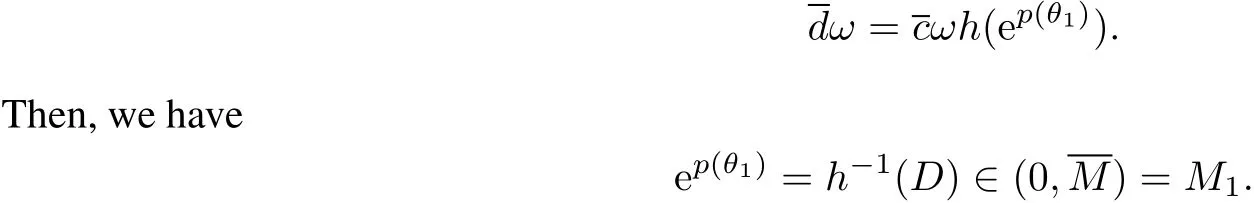
From(13),(14),(16)and p(t)＜ln M,we have

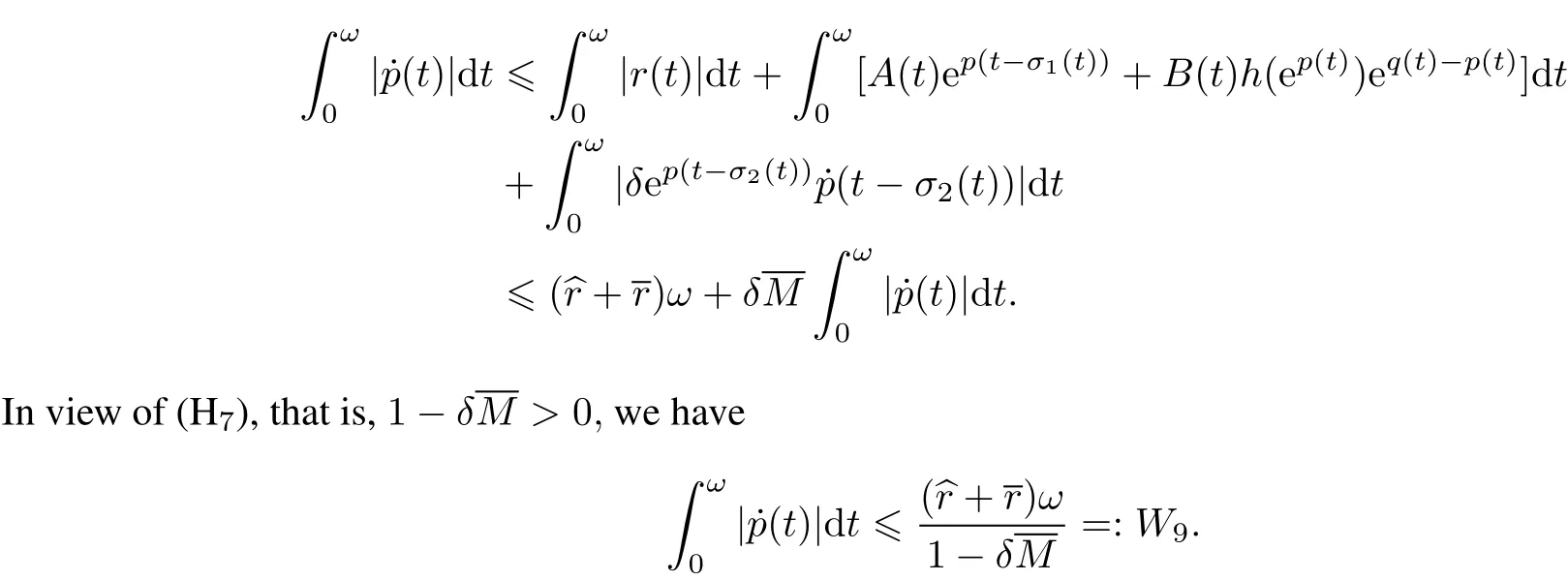
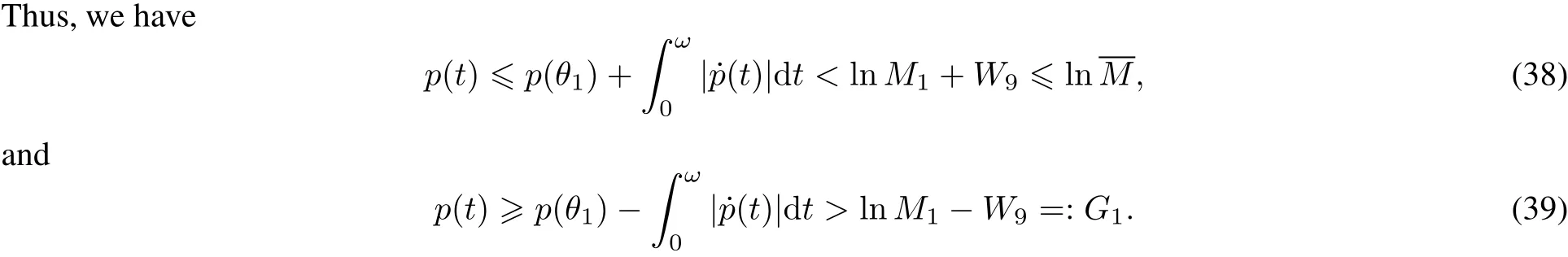
Itfollows from(38)and(39)that

Moreover,itfollows from(14),(38)and(40)that

Bωh(e G1)e q(η?)?ln M≤rω.

Thatis,

which,together with(17),leads us to

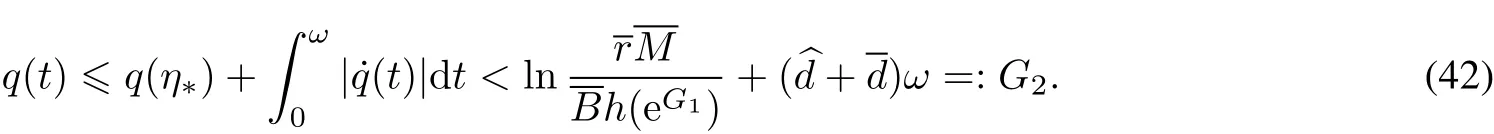
From(H6)and(H7),itis easy to see that r?A M＞0.Itfollows from(14),(37)and(40)that

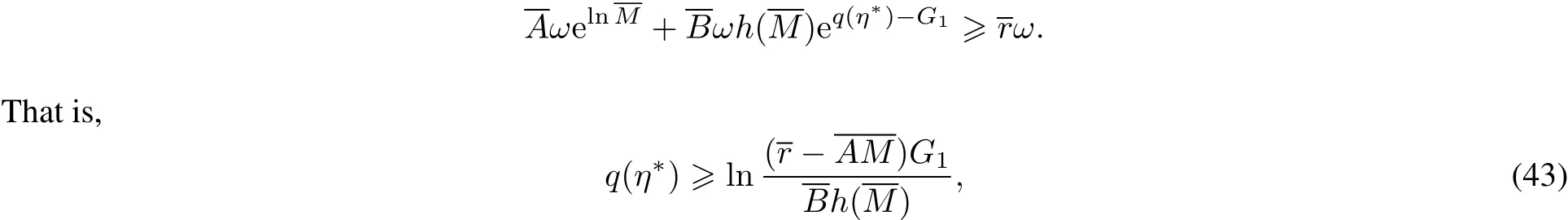
which,combined with(17),leads us to

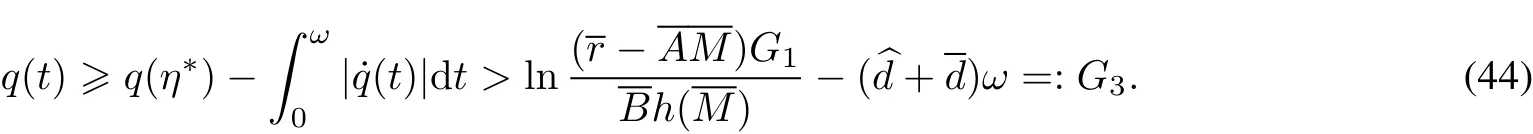
Therefore,from(42)and(44),we have

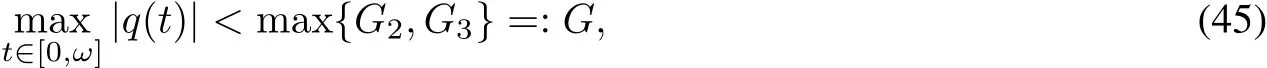
for p(t)∈(G1,ln M).

Case 2:p(t)＞ln M,t∈[0,ω].From(14),(H6)and the non-monotonic condition,there existsθ2∈[0,ω] such that

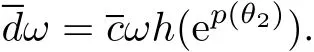
Then,we have

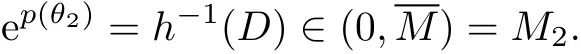
Combining this with(28)and(H7),we get

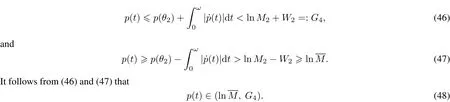
Since h(x)is decreasing for x∈(M,∞),itfollows from(14),(37)and(48)that

Moreover,itfollows from(14),(37)and(48),and condition(H6)r?＞0 that

Therefore,from(50)and(52),we have

for p(t)∈(ln M,G4).Obviously,M1,M2,ln M,G1,G3,G,G are independent ofλ.Consider the equation QNz=0,within z=(p,q)T∈R2,i.e.,(36)and the non-monotonic condition(H6),we show that(36)has two distinctsolutions

Choose C1＞0 such that

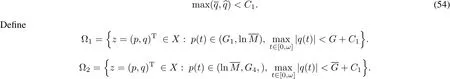
Both?1and?2are bounded open subsets of X.It follows from the non-monotonic condition,(45)and(53)that (p,q)T∈?1,(

)T∈?2.In view of(45)and(53),we have?1∩?2=?.Thus,?i,i=1,2 satisfy condition (a)of Lemma 3.Furthermore,QNz/=0 for z∈??i∩Ker L=??i∩.It is not difficult to verify that deg{JQN,?i∩Ker L,0}/=0.Thus,?isatisfy allthe conditions of Lemma 3.Hence,Lz=Nz has atleasttwo ω-periodic solutions z?=(p?,q?)Tand z?=(p?,q?)Twith z?∈Dom L∩and z?∈Dom L∩,and?,?are different.Therefore,()T,()Tare two differentpositiveω-periodic solutions of(6).

6 Application

In this section,we will present an application of Theorems 1,2,3,4.Consider the following non-monotonic periodic system

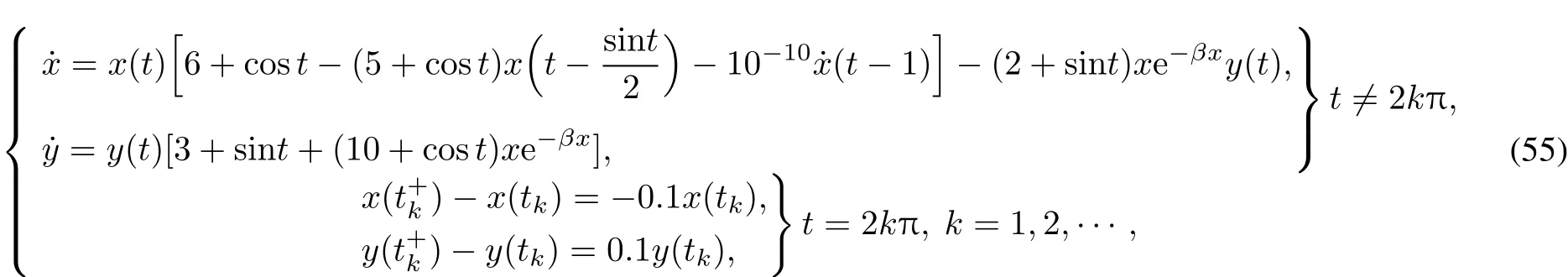
Theorem 6 Suppose that

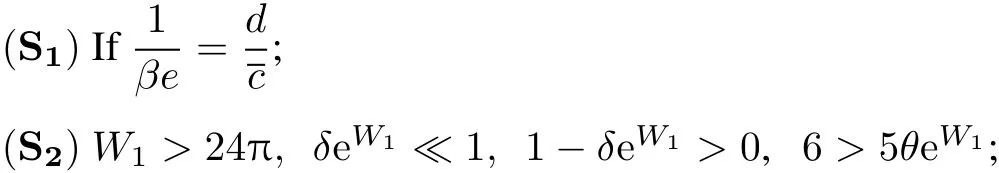
(S3)δ(t)=δis constant;˙σ1(t)＜1,˙σ2(t)＜1,¨σ2(t)=0 for t∈R.

Then,system(55)has atleastone positiveω-periodic solution.

Theorem 7 Suppose that

(S3)δ(t)=δis constant;˙σ1(t)＜1,˙σ2(t)＜1,¨σ2(t)=0 for t∈R;

(S5)1?δeW1＞0,1?δM＞0,r?＞0,r?＞0,ln M1+W2≤lnln M2?W2≥ln M. Then,system(55)has atleasttwo positiveω-periodic solutions.

[1]Holling C S.The functionalresponse ofpredatorto prey density and its role in mimicry and population regulation[J].Men Ent Sec Can,1965,45:1-60.

[2]Xiao D,Ruan S.Multiple bifurcations in a delayed predator-prey system with nonmonotonic functional response[J].J Differential Equations,2001,176:494-510.

[3]Chen Y.Multiple periodic solution of delayd predator-prey systems with type IV functionalresponses[J].Nonliear Analysis:RWA,2004,5:45-53.

[4]Xia Y H,Cao J,Lin M.Discrete-time analogues of predator-prey models with monotonic or nonmonotonic functional responses[J].Nonlinear Analysis,2007,8(4):1079-1095.

[5]Xia Y H,Cao J,Cheng S S.Multiple periodic solutions of a delayed stage-structured predator-prey modelwith nonmonotone functionalresponses[J].Appl Math Modelling,2007,31(9):1947-1959.

[6]Xing Y,Xia Y.Diversities of periodic solutions for a class of ecologicalmodel[J].Adv Diff Equat,2012,108:1-18.

[7]Du Z,Feng Z.Periodic solutions of a neutral impulsive predator-prey model with Beddington-DeAngelis functional response with delays[J].J Comput Appl Math,2014,258:87-98.

[8]Xia Y,Wang H,Kou K,Hu Z.Periodic solution of a higher dimensional ecological system with feedback control[J].J Appl Anal Comput,2016,6:3.

[9]Gaines R E,Mawhin J L.Coincidence degree and nonlinear differentialequations[M].Berlin:Springer,1977.

[10]Lu S,Lu S P,Ge W G.On the existence of positive periodic solutions for neutral functional differential equation with multiple deviating arguments[J].Acta Mathematicae Applicatae Sinica(English Series),2003,19(4):631-640.

[11]Lu S.On the existence ofpositive periodic solutions to a Lotka-Volterra cooperative population modelwith multiple delays [J].Nonlinear Anal,2008,68:1746-1753.

O 193 Documentcode:A Article ID:1000-5137(2017)03-0343-15

10.3969/J.ISSN.100-5137.2017.03.002

date:2017-03-27

This research was supported by the NationalNaturalScience Foundation of China under Grant(11671176, 11271333);Natural Science Foundation of Zhejiang Province under Grant(Y15A010022);the Scientific Research Funds of Huaqiao University and China Postdoctoral Science Foundation(2014M562320).

?Corresponding author:Xia Yonghui,Minjiang-Distinguished Professor,main research area:differential equation and dynamic systems.E-mail:xiadoc@163.com;xiadoc@hqu.edu.cn