Analysis ofa stage-structured mosquito population model

Fang Jinping1,2,Wan Hui1,2?
(1.Jiangsu Key Laboratory for NSLSCS,Nanjing Normal University,Nanjing 210046,China; 2.Schoolof Mathematical Sciences,Nanjing Normal University,Nanjing 210046,China)

In orderto study the impactoflimited resource and maturation time on mosquito population dynamics,we formulate a simple stage-structured mosquito population modelwith saturated recruitment rate,where mosquito population is divided into two class.The basic investigation of the model,such as the existence of equilibria and their stability,has been finished.The global stability of the unique endemic equilibrium has been proved.A numericalsimulation has been presented too.Our findings finally show thatreducing the resource and maturation time,are effective methods to controlthe number of mosquitoes.

mosquito;resource;maturation time;stage-structured model;stability

2010 MSC:92D30,34C60,34C23

1 Introduction

Mosquito is the vector of many diseases,like malaria,dengue,West Nile virus,etc.As we know,mosquitoborne diseases kill more people than any other diseases caused by single factor.In order to control these diseases, it is essential to understand mosquito population dynamics,to consider how resource and temperature can affect mosquito population,and affectmosquito-borne disease transmission.

Mosquito life includes fourstages:egg,larva,pupa,and adult.Each of these stages can be easily recognized by theirspecialappearance.The duration ofthe whole cycle,from egg laying to an adultmosquito eclosion,varies between 7 and 20 days,depending on the ambienttemperature ofthe swamp and the mosquito speciesinvolved[1].Only the adultfemale mosquitoes bite human beings and animals in orderto take blood meals,and the male mosquitoes feed only on plantjuices.Female mosquitoes feed on man,domestic animals,such as cattle,horses,goats,etc;all species of birds including chickens and ducks;alltypes ofwild animals including deer,rabbits;and they also feed on snakes,lizards,frogs,and toads.Female mosquitoeswillnotlay viable eggs withoutblood meals.Therefore,the abundance ofmosquito in a region is closely related to the blood mealresources available in the region[2].

Since only the adultfemale mosquitoes are responsible fortransmitting diseases,therefore in general,models focus only on describing the dynamics ofadultfemale mosquitoes.There have been extensive dynamicalmodeling studies ofthe mosquito population and mosquito-borne diseases(see[3–12]etc.)

We note that few models mentioned above includes the immature mosquito stage which is more sensitive to climate change and resource.Itis ouraim to formulate a mosquito population modelto include the immature stage to investigate the impact of limited resource and maturation time on the transmission dynamics of mosquito-borne diseases.

The restof the paper is organized as follows.In Section 2,the derivation of a new modelis given.We analyze the dynamics of this modelin Section 3,including the existence and stability of equilibria.Finally,we presentsome numericalsimulations and comments on our findings in Section 4.

2 Model

We group the three aquatic stages of mosquitoes into one class and divide the mosquito population into only two classes.one class consists ofthe firstthree stages,denoted by J,and the otherone ofwhich consists ofalladults, denoted by N.In order to depictthe impactof limited resource on mosquito reproduction,we letthe birth function, thatis,the oviposition function ofadults bWe letαbe the maturation rate oflarvae.The death rate oflarvae is a linearfunction(d+dJ),which d and d are the density independentand dependentcoefficients,respectively,

0101

and the death rate of adults is a constantμv.The stage-structured population dynamics of mosquitoes is given by:

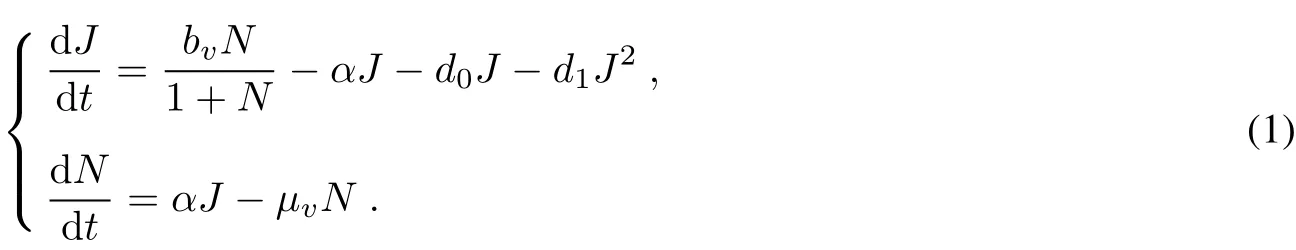
3 Dynamicalanalysis

Obviously,(0,0)is an equilibrium of(1).The localstability ofthe trivialequilibrium can be determined by the eigenvalues of the Jacobian matrix at(0,0)which has the form of

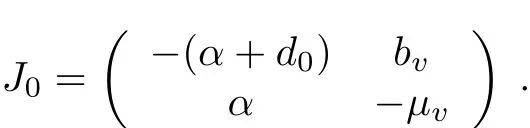
Define the netreproductive numberfor system(1)as

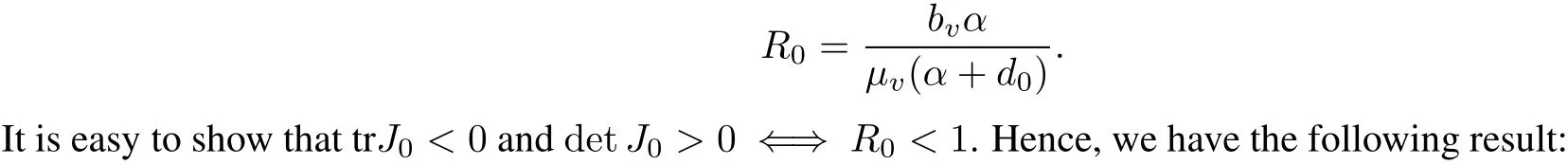
Theorem 1 The trivialequilibrium(0,0)is locally asymptotically stable if R0＜1.On the otherhand,(0,0) is unstable if R0＞1.

Ifthere exists a positive equilibrium ofsystem(1),itsatisfies

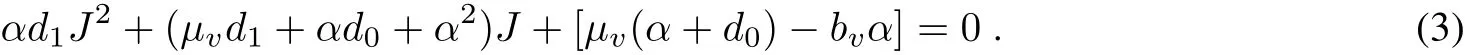
Hence,there exists a unique positive solution,denoted by(J?,N?),if and only ifμv(α+d0)?bvα＜0 which implies R=＞1.0

We nextwork on the stability of the positive equilibria.

The local stability of the positive equilibrium(J?,N?)can be determined by the eigenvalues of the Jacobian matrix atthe positive equilibrium which has the form of

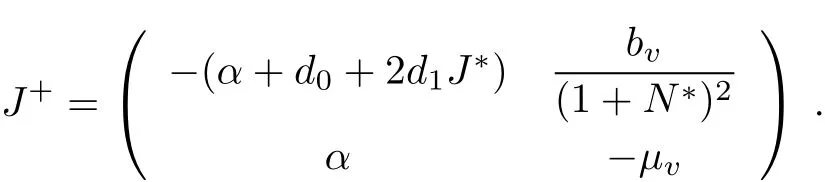
Itis easy to show thattr J+＜0.

And,the equations(2a)and(2b)lead to

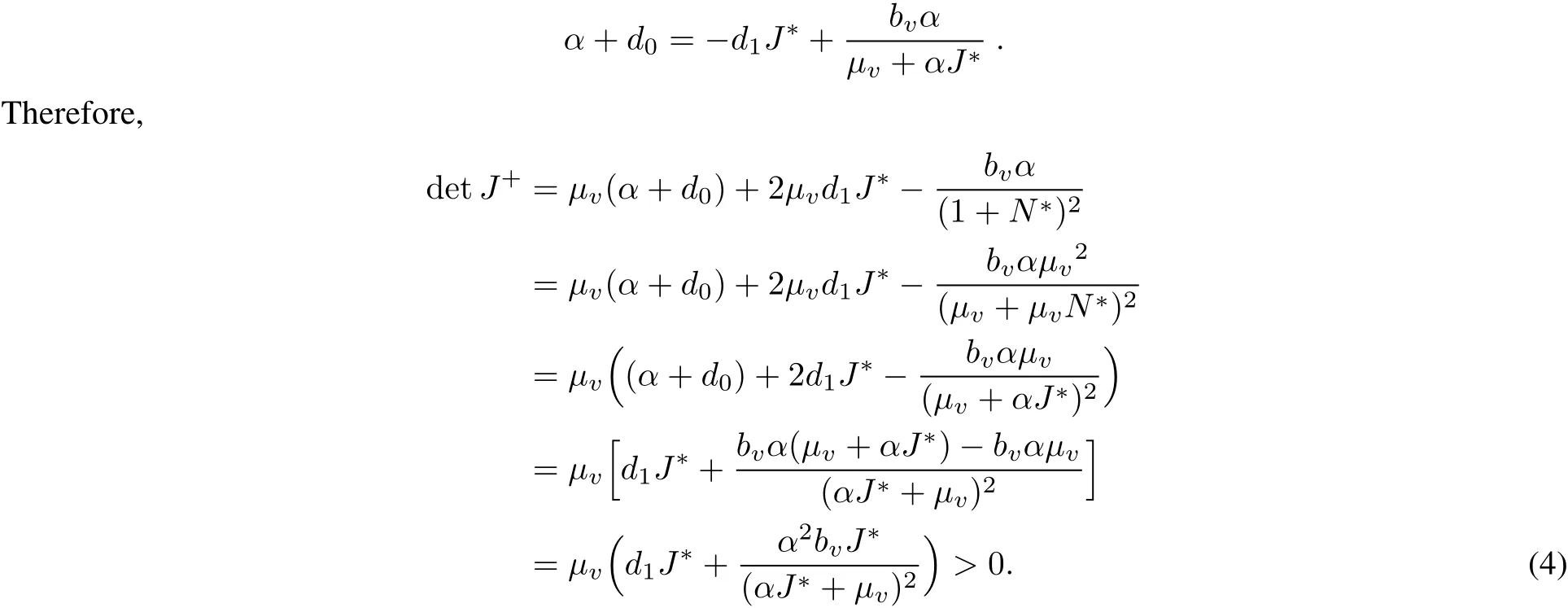
Hence the positive equilibrium is a locally asymptotically stable node.

Forsimplicity,we denote the two expression on the righthand side ofsystem(1)by f1(Jv,Nv)and f2(Jv,Nv).

Then,itis easy to check that

Thus,by the Bendixson-Dulac Principle,system(1)has no closed orbits in the positive quadrantof JN-plane.So, the positive equilibrium is globally asymptotically stable.In summary,we have the following results.

Theorem 2 If R0＜1,the trivialequilibrium(0,0)of system(1)is a locally asymptotically stable node,and there exists no positive equilibrium.If R0＞1,the trivialequilibrium(0,0)ofsystem(1)is unstable,and there exists a unique positive equilibrium,which is globally asymptotically stable.

4 Discussion

Table 1 Description of parameters of the models

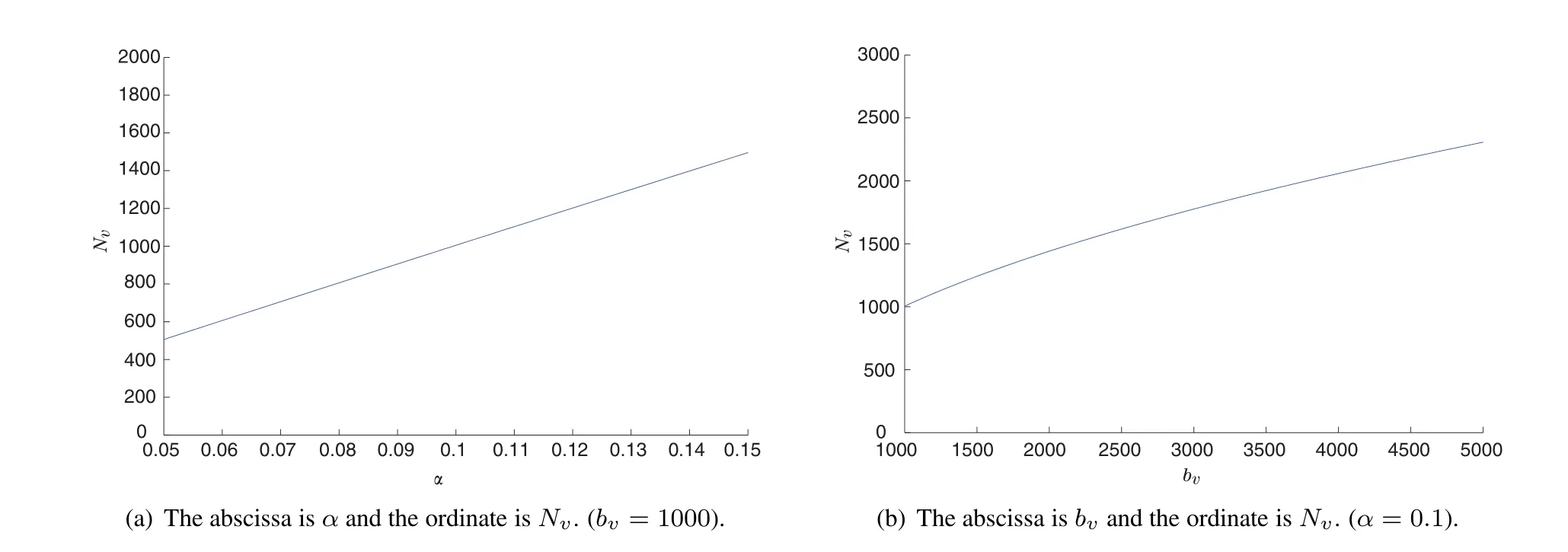
Figure 1 The value of adultmosquitoes atthe positive equilibrium.The parameter values are depicted in Table 1 exceptforα and bv.

In this paper,in orderto study the impactof limited resource and maturation time on the population dynamics of mosquitoes,we formulated a stage-structured mosquito model.The formula of the reproductive number for mosquitoes has been derived.We also explored the existence and stability of equilibria.Especially,the global stability ofthe unique positive equilibrium has been proved.

In order to study the impact of maturation time and limited resource,we draw the curve of the number of adultmosquitoes atthe positive equilibrium using some parameter values listed in Table 1 with respecttoαand bv, respectively.Simulation result Fig.1(a)manifests thatthe number of mosquitoes is a monotonic increasing function ofαwhich implies that with the increasing of temperature,the maturation time 1/αbecomes smaller,there will be more mosquitoes in a given region.Another result Fig.1(b)tells us that the abundance of the resource related to mosquito reproduction affects the number of mosquitoes positively.Some human behaviors,like pouring water, spraying insecticide,which can reduce the abundance of resource,are effective methods to control the number of mosquitoes and in turn to controlmosquito-borne diseases.

References:

[1]Gtles H M,Warrel D A.Bruce-Chwatts essentialmalariology,3rd Edition,Heinemann Medical Books[M].Portsmouth: New Hampshire,1993.

[2]Hard J J,Bradshaw WE.Reproductive allocation in the western tree-holo mosquito[J].Aedes Sierrensis,1993,66(1):55-65.

[3]Ngwa G A,Shu W S.A mathematical model for endemic malaria with variable human and mosquito populations[J]. Mathematicaland Computer Modelling,2002,32(7):747-763.

[4]Wan H,Cui J A.A model for the transmission of malaria[J].Discrete and Continuous Dynamical Systems-B,2009, 11(2):479-496.

[5]Wan H,Zhu H P.Backward bifurcation in compartmentalmodels for WestNile virus[J].Mathematical Biosciences,2010, 227(1):20-28.

[6]Wan H,Zhu H P.The impactofresource and temperature on malaria transmission[J].Journalof BiologicalSystems,2012, 20(3):285-302.

[7]Wan H.Modelling mosquito population dynamics:The impact of resource and temperature[J].Advanced Materials research,2013,726(731):156-159.

[8]Wan H,Zhu H P.A new modelwith delay for mosquito population dynamics[J].Mathematical Biosciences and Engineering,2014,11(6):1395-1410.

[9]Cooke K,Dritessche P V D,Zou X.Interaction ofmaturation delay and nonlinearbirth in population and epidemic models [J].JMath Biol,1999,39(4):332-352.

[10]Esteva L,Vargas C.Influence ofverticaland mechanicaltransmission on the dynamics ofdengue disease[J].Mathematical Biosciences,2000,167(1):51-64.

[11]Wonham M J,Beck T D,Lewis M A.An epidemiologicalmodelfor westnile virus:invasion analysis and controlapplications[J].Proceedings of the Royal Society,London Ser B,2004,271(1538):501-507.

[12]Chitnis N,Cushing J M,Hyman JM.Bifurcation analysis of a mathematicalmodelfor malaria transmission[J].SIAM J Appl Math,2006,67(1):24-45.

[13]Newton E A C,Reiter P.A model of the transmission of Dengue fever with an evaluation of the impact of ultra-low volume(ULV)insecticide applications on Dengue epidemics[J].American Journal of Tropical Medicine and Hygene, 1992,47(6):709-720.

[14]Coutinho F A B,Burattint M N,Lopez L F,etal.Threshold conditions for a non-autonomous epidemic system describing the population dynamics ofdengue[J].Bulletin of Mathematical Biology,2006,68(8):2263-2282.

[15]Fang J,Stephen A G,Lou Y J.Stage-structured models of intra-and inter-specific competition within age classes[J].J DifferentialEquations,2016,260(2):1918-1953.

[16]Munga S,Minakawa N,Zhou G.Survivorship ofimmature stages of Anopheles gambiae s.l.(Diptera:Culicidae)in natural habitats in western Kenya highlands[J].Journalof MedicalEntomology,2007,44(5):58-764.

O 29,O175.12,O175.13 Documentcode:A

1000-5137(2017)03-0417-05

10.3969/J.ISSN.100-5137.2017.03.010

date:2017-03-17

This research was supported by the NationalNaturalScience Foundation of China(11201236);the NSF of the Jiangsu Higher Education Committee of China(15KJD110004)and A ProjectFunded by PAPD of Jiangsu Higher Education Institutions.

Wan Hui,associate professor,research area:biomathematics,E-mail:wanh2046@163.com