Asynchronous HHH∞State Dependent Switching Control of Discrete-time Systems With Dwell Time
Rong Li
Asynchronous HHH∞State Dependent Switching Control of Discrete-time Systems With Dwell Time
Rong Li1
For a class of switched linear systems,we propose a dwell time strategy depending on the state of systems.This switching strategy not only makes the asynchronous H∞state-feedback switched systems stable but also shortens the active time.A new result on stability and l2-gain analysis for switched systems is given where the Lyapunov functions are allowed to be increasing during the running time of subsystems,at the same time,the Lyapunov functions do not contain the limit ofμ.By using the dwell time strategy depending on the state of systems,sufficient conditions for the desired H∞controller of switched linear systems are derived.Then the result is expanded to nonlinear switched systems.A numerical example is provided to demonstrate the e ff ectiveness of the proposed design approach.
Asynchronous H∞state-feedback switched systems,discrete-time systems,dwell time strategy
DOI10.16383/j.aas.2017.e150291
1 Introduction
Switched systems,which are efficiently used to model many physical or man-made systems displaying features of switching,have been extensively studied over the past decades.Typically,switched systems consist of a fi nite number of subsystems(described by di ff erential or di ff erence equations)and an associated switching signal governing the switching among them.The switching signals may belong to a certain set and the sets may be various.This di ff erentiates switched systems from general systems,since the solutions of the former are dependent on both system initial conditions and switching signals.Many physical processes exhibit switched and hybrid behavior[1]?[3],and switching frequently occurs in many engineering applications.Due to the theoretical development as well as practical applications,analysis and synthesis of switched system have recently gained considerable attention[4]?[10].
Recently,the H∞control problem of switched systems has stirred renewed research interests[11]?[19].The goal is to design a controller to stabilize a system while satisfying an H∞-norm bound constraint on disturbance attenuation.Sufficient conditions for designing a robust H∞controller with time-varying norm-bounded uncertainty are studied by means of hybrid state feedback strategy in[12].By average dwell time methods[13],investigated the H∞controller of switched system with uncertain inputs.
While,considering the H∞state feedback problem,a very common assumption is that the controller is switched synchronously with the switching of system modes,which is quite impractical.In engineering application,since it inevitably takes some time to identify the active subsystem and apply the matched controller,the real switching time of controllers may lag behind that of practical subsystems,that is to say,there exists asynchronous switching between the controllers and system mode.The necessities of considering asynchronous switching for efficient control design have been shown for mechanical or chemical systems in[20].Recently,the asynchronous switching problem has been investigated,and some results are obtained in the studies of switched system[21]?[26].The stabilization of asynchronous linear system has been included in[21].Stability,l2-gain and asynchronous control of discrete-time switched systems are considered in[23].Then,the results are condensed to fi lter in[26],which discusses the stability and l2-gain of switched linear systems.
The stability analysis of switched systems with dwell time has received a considerable attention in the last decade[27]?[30].The method there do not guarantee any minimal dwell time.The practical case,however,is that some minimal time period between consecutive switching is required.Arbitrarily fast switching may cause large state transients at the switching points.A dwell time may be required for these transients to subside.This is one of the reasons why the area of switched systems with dwell time is becoming increasingly popular.At the same time,it is found that the most stabilizing switching law for many switched systems with unstable subsystems obeys some dwell time.Adding a dwell time constraint to a suboptimal switching law may thus achieve better results.
In this paper,the robust asynchronous H∞state dependent switching of linear system with dwell time is considered.About switching signals,some works have been done in[27]?[30].Combined stabilizing strategies are proposed in[27],and the result is improved in[27].Statedependent switching laws have been fi rst considered in[27].The method there do not guarantee any dwell time.It has been shown in[27]that the most destabilizing switching law of a switching law for a switched system with stable subsystems applies a dwell time.Using the same analysis,it can be seen that the most stabilizing switching law for asynchronous switched systems obeys some dwell time.Adding a dwell time constant to switching law may achieve better results.Thus in our paper,minimal dwell time is introduced,which not only meets the need of minimal time between consecutive switching,but also compensates the possible increment introduced by the asynchronous phenomenon between the system modes and controllers.On the other hand,the dwell time strategies depending on state not only reduce the time of being active,but also make that the Lyapunov function does not have the limit ofμ.All of these motivated us to study the H∞controller of asynchronous switched system,which is unstable within the unmatched interval of(klkl+1),?l∈ N.
The asynchronous H∞control problem for a class of state dependent switching system with dwell time is investigated in this paper.Based on the dwell time approach depending on state,sufficient conditions are developed forthe H∞control system.It is noted that subsystems are allowed to be unstable within the unmatched interval of the interval(klkl+1),?l∈ N.Then,the corresponding solvability condition for the desired controller is established.
The remainder of this paper is organized as follows.The asynchronous H∞control of switched systems is formulated in Section 2.Section 3 is devoted to derive the results on stability and l2-gain analyses and formulate the problem of asynchronous H∞control for discrete-time switched system.A numerical example is given in Section 4,and then,we make a conclusion about this article in Section 5.
Notation:The notations used throughout the paper are standard.Rndenotes the n-dimensional Euclidean space;Nrepresents the set of nonnegative integers;the notation P>0 means that P is real symmetric and positive de fi nite;l2[0,∞)is the space of square-integrable vector functions over[0,∞);‖·‖denotes the Euclidean norm of a vector and its induced norm of a matrix.In symmetric matrices or long matrix expressions,we use a star(?)to represent a term that is induced by symmetry.
2 Problem Description and Preliminaries
Consider a class of switched linear systems given by(1).

where x(k)∈Rnis the state vector;u(k)∈Rmis the control input;ω(k)∈ Rpis the disturbance input which belongs to l2[0,∞),z(k)∈ Rqis the controlled output;σ is a piece wise constant function of time k called a switching signal,which takes its values in the fi nite set I={1,...,N},and N>1 is the number of subsystems.
In the paper,we design an H∞state feedback controller with the following general structure.

where Ki∈Rm×nare matrices to be determined.
It is assumed that the subsystem is activated at the switching instant kl,?l∈ N.Owing to the fact,real switching time of controllers exceeds or lags behind that of the practical subsystems,so the switching instant of the controller is kl+ Δl,?l∈ N,where Δl> 0 represents the unmatched time during which the switched system maybe unstable.
Therefore,by substituting u(k)into system(1),we obtain the closed-loop system as
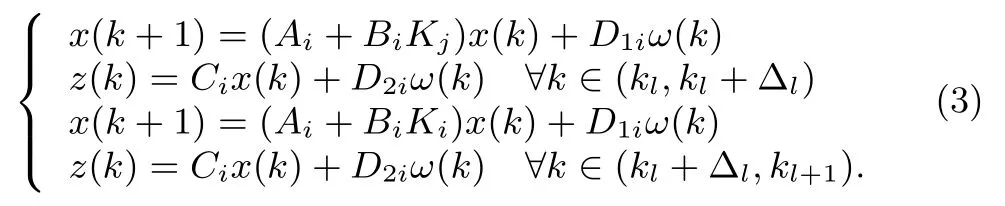
Choose the Lyapunov functional candidate of the form
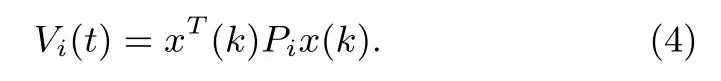
The subsequent switching time/index sequences are defi ned as following Choose the Lyapunov functional candidate of the form

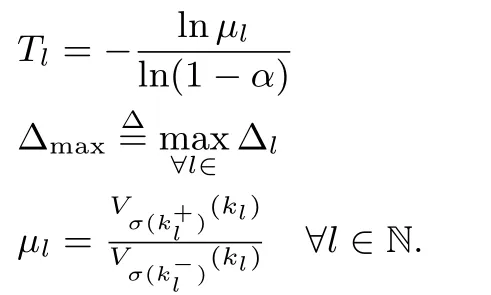
According to this strategy,when the lth subsystem is activated,it should be active for the minimal dwell time Δ to compensate the possible increment which is introduced by mismatching of controllers and subsystems.Besides,ifμl> 1 the subsystems will be active for another Tl=lnμl/lnα to compensate the possible increment in switching instants,else the system will switch to the jth subsystem immediately.
Remark 1:In this note,we propose a dwell time strategy depending on the state of subsystems.On one hand,whenμl> 1 the increment will be compensated by more speci fi c decrement,in other words,the subsystem will be active for another Tl.Whenμl< 1 the system will switch to another subsystem immediately.So we can get the conclusion that the active time of subsystem speci fi ed by dwell time strategy depending on the state of system is shorter than that of the system speci fi ed by normal dwell time strategy;on the other hand,it is easy to see that the Lyapunov function does not have the limit of Pi< μPj,?i,j∈ I.
We give the following de fi nition,which will play an important role in deriving our main results subsequently.
De fi nition 1:Given a constant γ>0,the switched system(3)is said to be stabilized with H∞disturbance attenuation γ via switching if there exists a switching rule such that under this switching,it satis fi es
1)System(3)with ω=0 is stable.
2)With zero-initial condition x(0)=0,‖z‖2<γ‖ω‖2holds for all nonzero.
3 Main Results
3.1 Stability and Performance Analysis
In this section,sufficient conditions on stability with an l2-gain are derived for system(3)via the dwell time strategies depending on the state of system.
Theorem 1:Given scalars 0<α<1, β>0 and the switching time instants k0< k1< ···< kl?1< kl,during[k0,kl],l=1,2,...,the closed-loop H∞control system is stable under the switching signal as described in the formula(5),if Vi(k)satis fi es
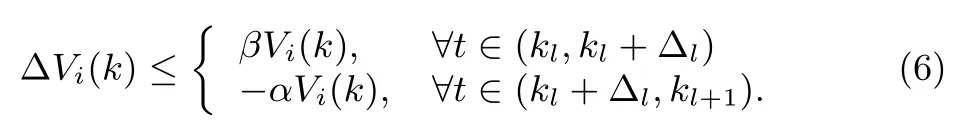
Proof:Denote ΔVi(k)=Vi(k+1)? Vi(k).Ifμl?1> 1,in other words the lth subsystem activates for Δl+Δ+Tl.
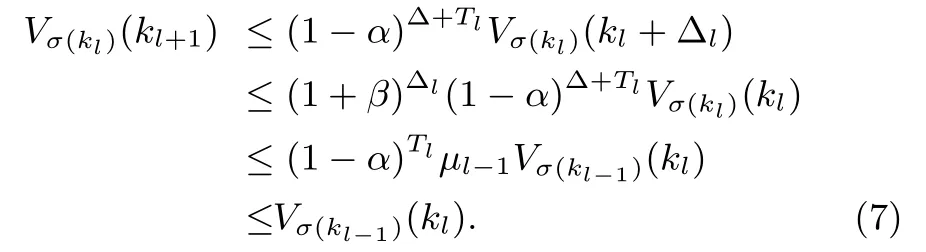
Ifμ<1,in other words,the lth subsystem activates for Δl+Δ.
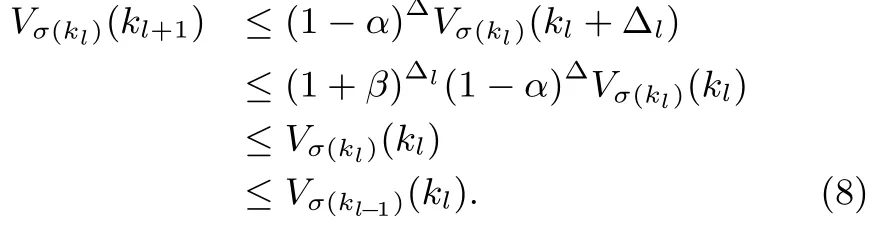
The switching signals stem from the requirement that the value of the Lyapunov function Vσ(k)(kl+1)is less than Vσ(kl?1).An alternative way to guarantee the decrease of V is to require that the value of V,for another T seconds after the switching,is less than the value it had just prior to the switching.The latter requirement is satis fi ed if the switching signals as described in(5)hold.
Therefore,we get the conclusion that the closed-loop system is stable.
Remark 2:Note that the switched systems are active in the intervals(consisting of matched and unmatched intervals)during which a subsystem may be unstable.In other words,the Lyapunov function gets increased in the unmatched intervals.However,the possible increment will be compensated by the more pronounced decrement(by limiting the lower bound of dwell time).Thus,we can get that the closed-loop system is stable.
Next,the H∞performance of the system(3)is given in the following theorem.
Theorem 2:Given scalars 0<α<1, β>0 and the switching time instants k0< k1< ···< kl?1< kl,during[k0,kl],l=1,2,...,the closed-loop H∞control system is stable and has an l2-gain no greater than γs,if Vi(k)satis fi es
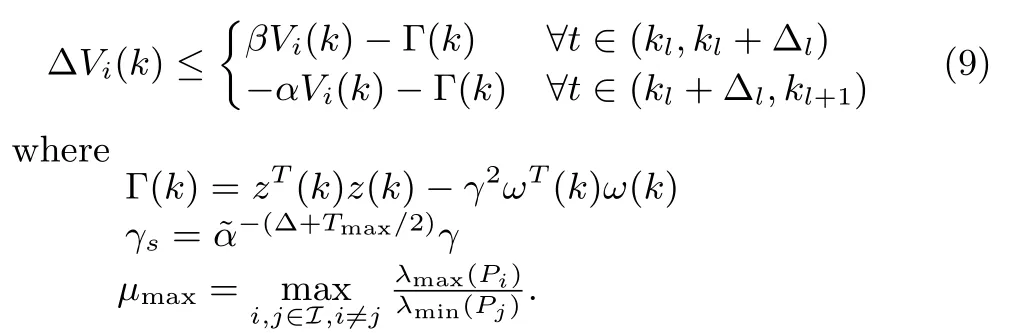
In order to study the asynchronous H∞controller for system(1),for conciseness,the time t1,t2,...,tk,...is set to switching instant.Without loss of generality,we assume thatμl?2> 1,μl?1< 1,...(for other situations we can get the same result through the same proof process),in other words kl=kl?1+ Δl?1+Tl?1,kl+1=kl+ Δl,....
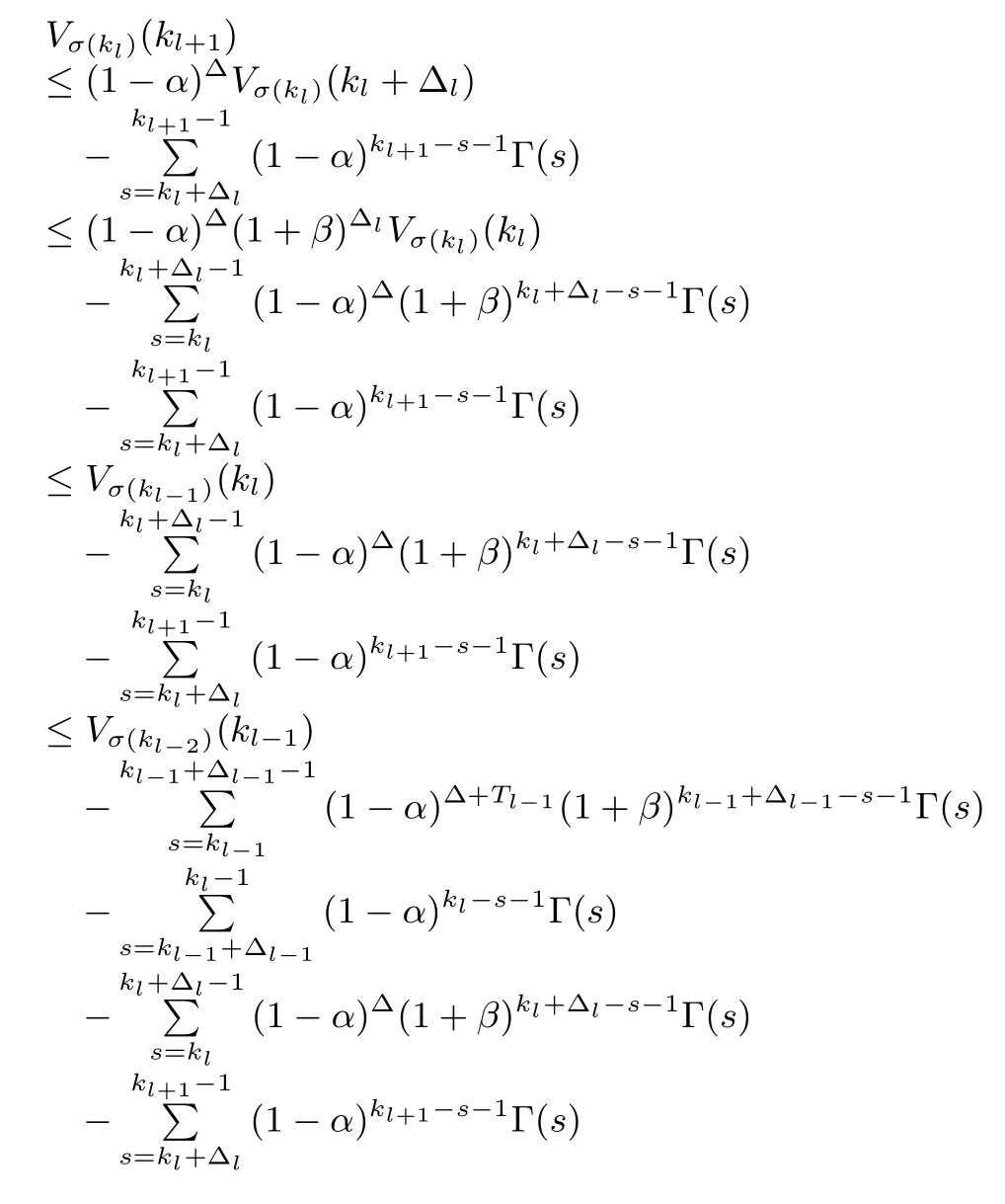

Under zero initial condition,we know that
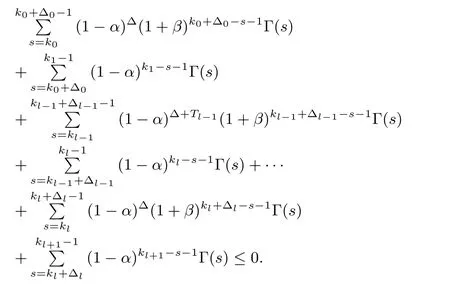
Therefore,we can obtain that
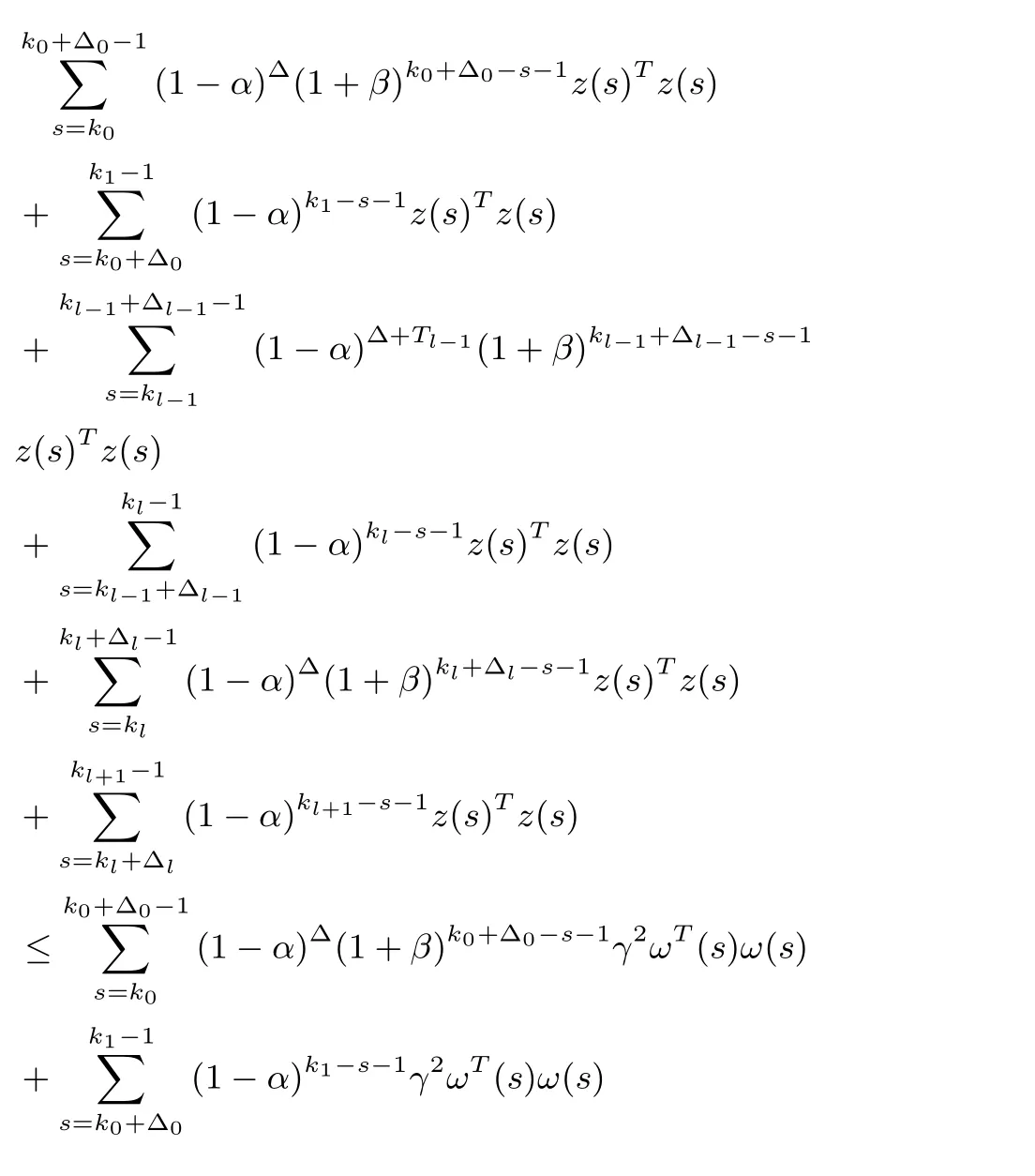
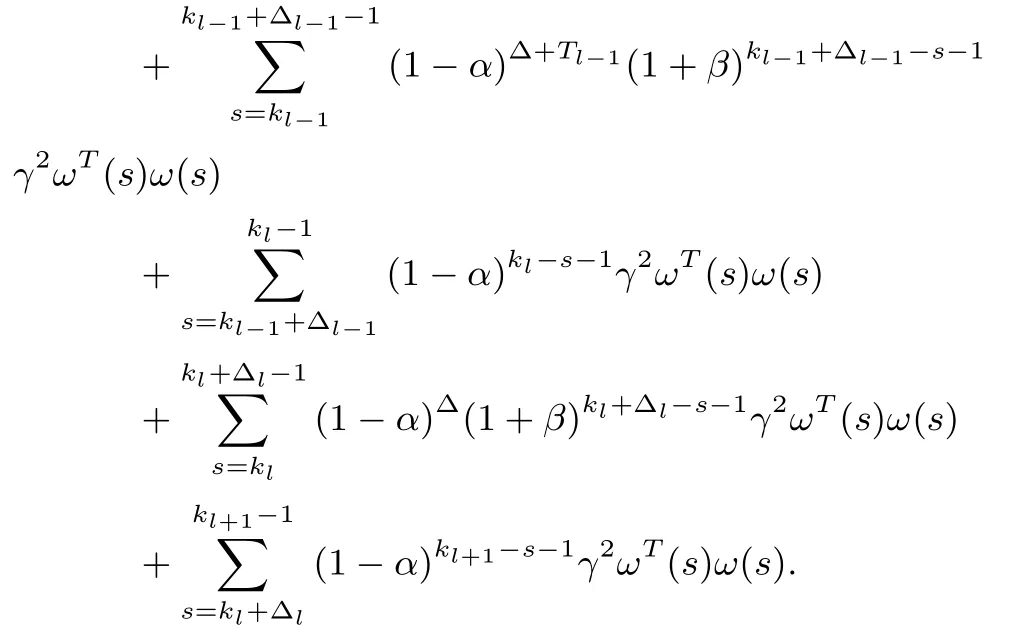
So we can get
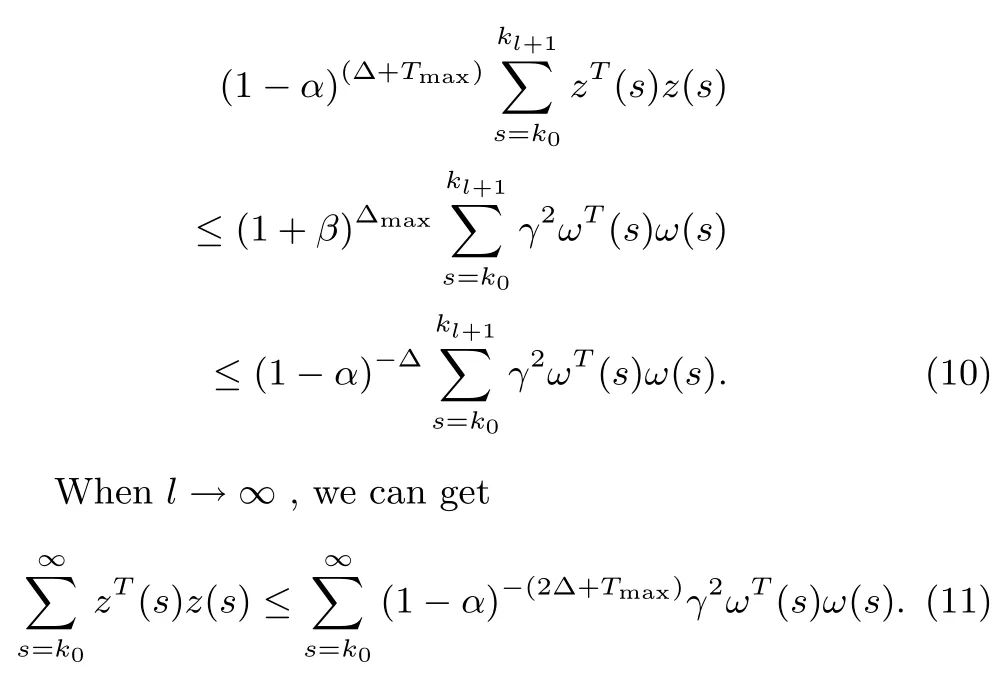
Remark 3:The proof of disturbance attenuation level is di ff erent from[24],in which the result is got under zero initial condition Vi(kl)=0,?l∈ I.In this paper,we provided a better result about weighted l2-gain under zero initial condition Vi(k0)=0;besides the result is suitable for any positive number Δmax,which does not contain limit of Tmax>1 in[24].
3.2 H∞Controller Design
Now,based on the conditions on stability with a l2-gain in Theorem 1 and Theorem 2,sufficient conditions for the existence of controller(2)are presented in the following theorem.Then,the admissible H∞controller parameters can be given.
Theorem 3:Consider switched linear system(3)and let 0<α<1,β>0 be given constants.If there exist matrices Si,Viand Ui,?i∈ I,such that for?i,j∈ I,i/=j,the following inequalities hold
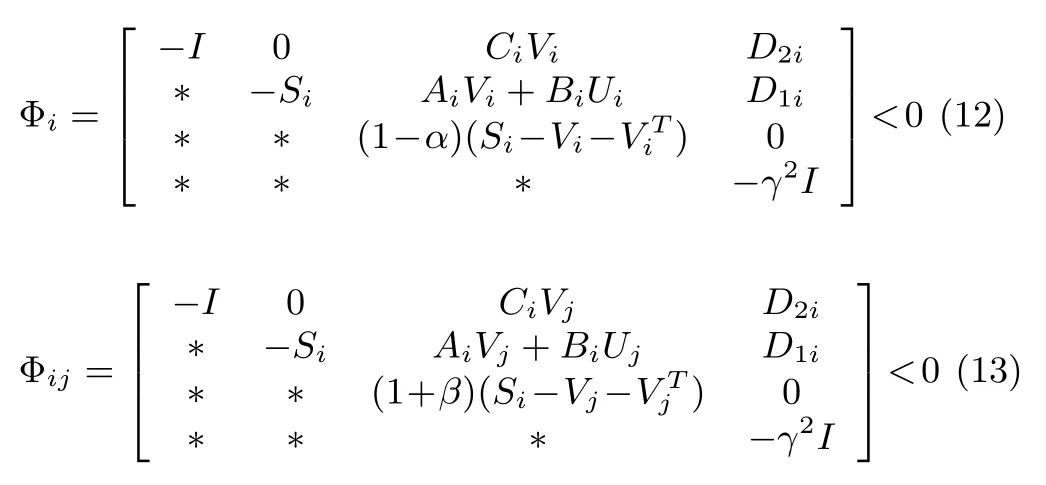
then there exists a set of mode-dependent stabilizing controllers with asynchronous delay such that system(3)is stable with an H∞performance index γsfor the switching signal(5).Moreover,if(13)and(14)have a feasible solution,the admissible controller can be given by

Proof:When t∈(tk+Δk,tk+1),we can get
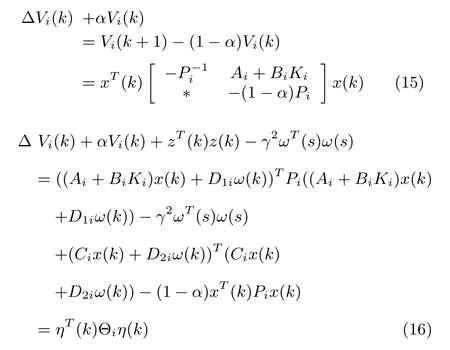
where η(k)=(xT(k),ωT(k))T.
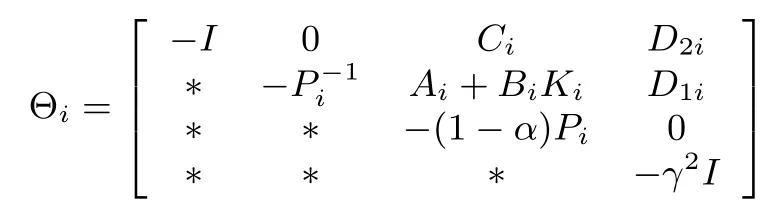
similarly,when t∈(tk,tk+Δk),we can get

Remark 4:In Theorem 3,the conditions of H∞stability are got for asynchronous switched linear system.We canget the same result for asynchronous switched system with nonlinear from(19).
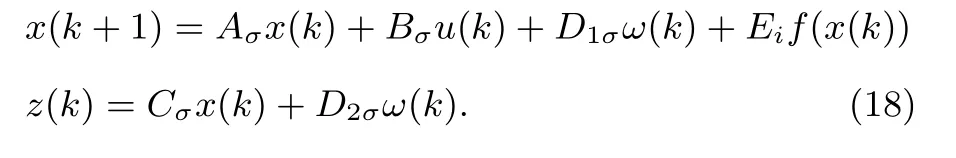
In this paper,without loss of generality,we always assume that f(0)=0.For vector-valued functions f,we assume:
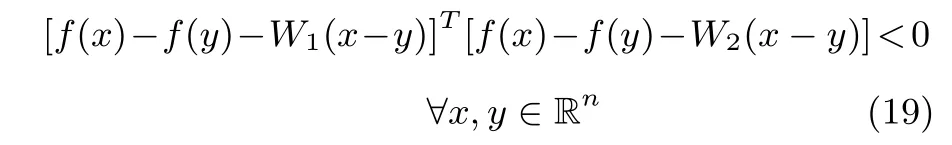
where W1,W2∈ Rn×nare known real constant matrices,and W1+W2is a positive de fi nite matrix[27].
Corollary 1:Consider switched nonlinear system(19)and let 0<α<1,β>0 be given constants and W1,W2be given matrices.If there exist matrices Si>0,Vi>0 and Ui,?i∈ I,such that for?i,j∈ I,i/=j,the following inequalities hold


Proof:From(20),we can get
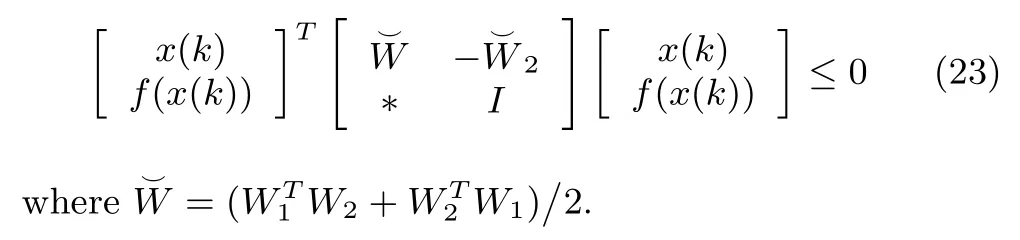
Follow the same line,together with(24),when t∈(tk+Δk,tk+1),we can get

Then performing a congruent transformation to the inequality Θi≤ 0 and Θij≤ 0 via diag'I I ViI“ and diag'I I VjI“,we can obtain(21)and(22).From Theorem 1 and Theorem 2,we can get that the closed-loop system is stable with an l2-gain.
4 Numerical Example
In this section,we give an example to demonstrate the e ff ectiveness of the proposed method.
Example:Considering the system(1)with two subsystems,and the parameters of each subsystem are given as follows:
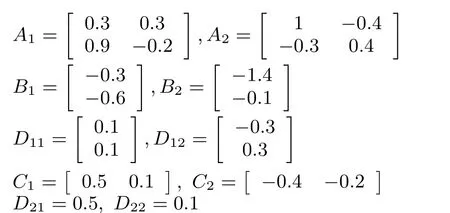
Let α =0.8, β =0.3,and Δmax=1,we consider the asynchronous switching in the design phase and turn to Theorem 2,by utilizing LMI Toolbox,we can get γ =2.5615,γs=4.5614 and the controller parameters are obtained as follow:K1=[1.2853 ?0.2038], K2=[0.8182 ?0.4078].
The simulation results are given in Figs.1 and 2.The switching signals are shown in Fig.1,the system state response under the switching signal is shown in Fig.2.From the simulation results,we can get that the switching signal of the controller is delayed by the switching signal of the subsystem,and the system state is stable under the design of switching signals.
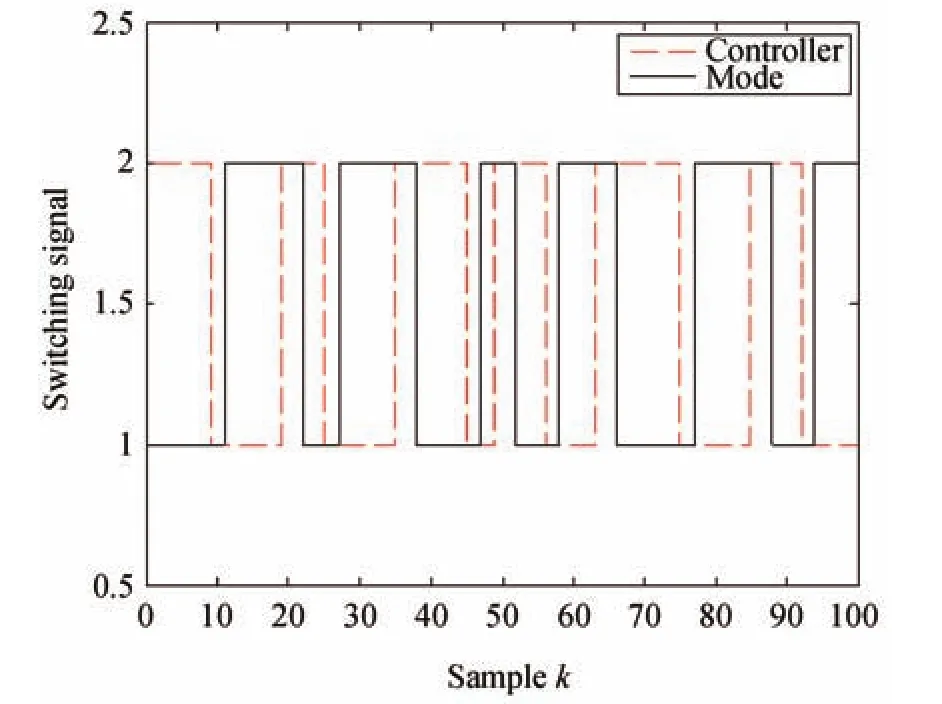
Fig.1. The switching signal.
Integrating the whole simulation results,we can get that the desired switched controller is feasible and e ff ective for systems(1)under the admissible switching signals.
5 Conclusion
A new method for the stability and l2-gain of statedependent switching law under dwell time constraint is introduced.By allowing the subsystems to be unstable within a bounded time of the interval[kl,kl+1),?l ∈ N,the more general conditions for H∞controller have been derived and formulated.Then the corresponding controller is obtained.An example is given to illustrate the validity of the obtained theoretical results.
1 D.Liberzon,Switching in Systems and Control,Boston,MA,USA:Birkhauser,2003.
2 Z.D.Sun,Switched Linear Systems:Control and Design,London,UK:Springer-Verlag,2005.
3 R.A.Decarlo,M.S.Branicky,S.Pettersson,and B.Lennartson,“Perspectives and results on the stability and stabilizability of hybrid systems,”Proc.IEEE,vol.88,no.7,pp.1069?1082,Jul.2000.
4 J.Daafouz,P.Riedinger,and C.Iung,“Stability analysis and control synthesis for switched systems:a switched Lyapunov function approach,”IEEE Trans.Automat.Control,vol.47,no.11,pp.1883?1887,Nov.2002.
5 J.P.Hespanha and A.S.Morse,“Stability of switched systems with average dwell-time,”in Proc.the 38th IEEE Conf.Decision and Control,Phoenix,USA,1999,pp.2655?2660.
6 D.Koenig and B.Marx,“H∞- fi ltering and state feedback control for discrete-time switched descriptor systems,”IET Control Theory Appl.,vol.3,no.6,pp.661?670,Jun.2009,doi:10.1049/iet-cta.2008.0132.
7 H.Lin and P J.Antsaklis,“Hybrid state feedback stabilization with l2performance for discrete-time switched linear systems,” Int.J.Control,vol.81,no.7,pp.1114?1124,2008.
8 L.Wu,D.W.C.Ho,and C.W.Li,“Stabilisation and performance synthesis for switched stochastic systems,”IET Contr.Theory Appl.,vol.4,no.10,pp.1877?1888,Jun.2010,doi:10.1049/iet-cta.2009.0179.
9 P.Mhaskar,N.H.El-Farra,and P.D.Christo fi des,“Robust predictive control of switched systems:Satisfying uncertain schedules subject to state and control constraints,”Int.J.Adapt.Control Signal Process.,vol.22,no.2,pp.161?179,Mar.2008.
10 G.M.Xie and L.Wang,“Stabilization of switched linear systems with time-delay in detection of switching signal,”J.Math.Anal.Appl.,vol.305,no.1,pp.277?290,May2005.
11 Y.E.Wang,J.Zhao,and B.Jiang,“Stabilization of a class of switched linear neutral systems under asynchronous switching,”IEEE Trans.Automat.Control,vol.58,no.8,pp.2114?2119,Aug.2013.
12 D.Xie and X.Chen,“Observer-based switched control design for switched linear systems with time delay in detection of switching signal,”IET Control Theory Appl.,vol.2,no.5,pp.437?445,May.2008.
13 Y.E.Wang,X.M.Sun,and B.W.Wu,“LyapunovCK-rasovskii functionals for input-to-state stability of switched non-linear systems with time-varying input delay,”IET Control Theory Appl.,vol.9,no.11,pp.1717?1722,Jul.2008.
14 I.Zamani,M.Sha fi ee,and A.Ibeas,“Stability analysis of hybrid switched nonlinear singular time-delay systems with stable and unstable subsystems,”Int.J.Syst.Sci.,vol.45,no.5,pp.1128?1144,2014.
15 A.Y.Aleksandrov and O.Mason,“Absolute stability and LyapunovCKrasovskii functionals for switched nonlinear systems with time-delay,”J.Franklin Inst.,vol.351,no.8,pp.4381?4394,Aug.2014.
16 L.X.Zhang and P.Shi,“Stability,l2-gain and asynchronous H∞control of discrete-time switched systems with average dwell time,”IEEE Trans.Automat.Control,vol.54,no.9,pp.2192?2199,Sep.2009.
17 Z.X.Xiang and R.H.Wang,“Robust control for uncertain switched non-linear systems with time delay under asynchronous switching,”IET Control Theory Appl.,vol.3,no.8,pp.1041?1050,Aug.2009.
18 L.X.Zhang and H.J.Gao,“Asynchronously switched control of switched linear systems with average dwell time,”Automatica,vol.46,no.5,pp.953?958,May 2010.
19 L.X.Zhang,N.G.Cui,M.Liu,and Y,Zhao,“Asynchronous fi ltering of discrete-time switched linear systems with average dwell time,”IEEE Trans.Circuits Syst.Regular Papers,vol.58,no.5,pp.1109?1118,May 2011,doi:10.1109/TCSI.2010.2092151.
20 Z.D.Sun,“Combined stabilizing strategies for switched linear systems,”IEEE Trans.Automat.Control,vol.51,no.4,pp.666?674,Apr.2006.
21 J.D.Xiong and Z.D.Sun,“An improved combined switching strategy for switched linear systems,”in Proc.2010 IEEE 26th Conv.Electrical and Electronics Engineers in Israel,Eliat,Israel,2010.
22 H.Ishii and B.A.Francis,“Stabilizing a linear system by switching control with dwell time,”IEEE Trans.Automat.Control,vol.47,no.12,pp.1962?1973,Dec.2002.
23 M.Margaliot and G.Langholz,“Necessary and sufficient conditions for absolute stability:the case of second-order systems,”IEEE Trans.Circuits Syst.Fundam.Theory Appl.,vol.50,no.2,pp.227?234,Feb.2003.
24 D.Liberzon,Switching in Systems and Control,Boston,MA:Birkhauser,2003.
25 J.C.Geromel and P.Colaneri,“Stability and stabilization of continuous-time switched linear systems,”SIAM J.Control Optim.,vol.45,no.5,pp.1915?1930,2006.
26 L.I.Allerhand and U.Shaked,“Robust stability and stabilization of linear switched systems with dwell time,”IEEE Trans.Automat.Control,vol.56,no.2,pp.381?386,Feb.2011.
27 Z.D.Wang,D.W.C.Ho,Y.R.Liu,and X.H.Liu,“Robust H∞control for a class of nonlinear discrete time-delay stochastic systems with missing measurements,”Automatica,vol.45,no.3,pp.684?691,Mar.2009.
28 H.Haimovich and M.M.Seron,“Bounds and invariant sets for a class of switching systems with delayedstate-dependent perturbations,”Automatica,vol.49,no.3,pp.748?754,Mar.2013.
29 Y.M.Wang,F.E.Alsaadi,S.Lauria,Y.R.Liu,“Robust H∞control for a class of discrete time-delay stochastic systems with randomly occurring nonlinearities,”Abstr.Appl.Anal.,vol.2014,Article ID 170794,2014.
30 Y.R.Liu,F.E.Alsaadi,X.Z.Yin,and Y.M.Wang,“Robust H∞fi ltering for discrete nonlinear delayed stochastic systems with missing measurements and randomly occurring nonlinearities,”Int.J.Gen.Syst.,vol.44,no.2,pp.169?181,2014.

Rong Li is studying for the Ph.D.degree at the School of Automation,Northwestern Polytechnical University(NWPU).He received the M.S.degree from NWPU,China,in 2013.His research interests include switching mode power and automation.E-mail:qaz1230808@126.com
Rong Li.Asynchronous H∞state dependent switching control of discrete-time systems with dwell time.Acta Automatica Sinica,2017,43(8):1418?1424
November 4,2015;accepted December 12,2016.
Recommended by Associate Editor Ximing Sun.
1.School of Automation,Northwestern Polytechnical University,Xi’an 710129,China

