ZOU Min,CHEN Rong-san,LIU An-ping

(School of Mathematics and Physics,China University of Geosciences,Wuhan 430074,China)

OSCILLATION OF NONLINEAR IMPULSIVE DELAY HYPERBOLIC EQUATION WITH FUNCTIONAL ARGUMENTS VIA RICCATI METHOD

ZOU Min,CHEN Rong-san,LIU An-ping

(School of Mathematics and Physics,China University of Geosciences,Wuhan 430074,China)

In this paper,we mainly deal with the oscillation problems of nonlinear impulsive hyperbolic equation with functional arguments.By using integral averaging method and a generalized Riccati technique,a sufficient condition for oscillation of the solutions of nonlinear impulsive hyperbolic equation with functional arguments is obtained.We can make better use of some existing conclusions about oscillation of the solutions of impulsive ordinary dif f erential equations with delay.

oscillation;impulsive;delay;hyperbolic equation;Riccati inequality

1 Introduction

The theories of nonlinear partial functional di ff erential equations are applied in many fi elds.In recent years the research of oscillation to impulsive partial di ff erential systems caught more and more attention.In this paper,we study the oscillation properties of the solutions to impulsive delay hyperbolic equation

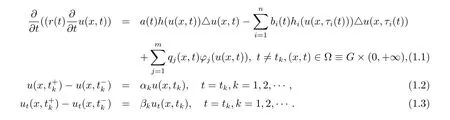
The following is the boundary conditionwhere G is a bounded domain of Rnwith the smooth boundary?G and n is the unit exterior normal vector to?G.

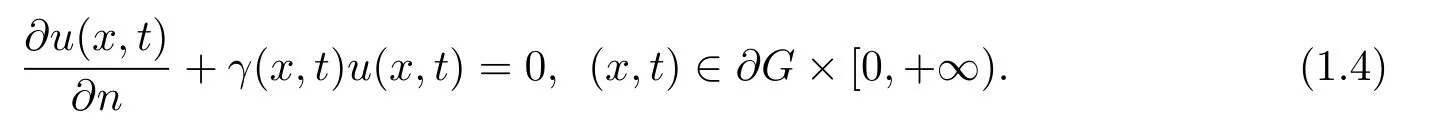
Following are the basic hypothesis

(H1)r(t)∈C([0,+∞);(0,+∞)),a(t),bi(t)∈PC([0,+∞);[0,+∞)),i=1,2,···,n.j=1,2,···,m,where PC denotes the class of functions which are piecewise continuous in t with discontinuities of the fi rst kind only at t=tk,k=1,2,···.

(H2)τi(t)∈C([0,+∞);R)=+∞,i=1,2,···,n.

(H3)h(u),hi(u)∈C(R,R),uh(u)≥0,uh′(u)≥0,≥0,i=1,2,···,n;φj(s)∈C(R,R),=const.＞0 for s 6=0.αk,βk=const.＞-1,0＜t1＜t2＜···＜tk＜

We introduce the notations

De fi nition 1.1The solution u(x,t)of the problems(1.1)-(1.4)is said to be nonoscillatory in domain Ω if it is either eventually positive or eventually negative.Otherwise,it is called oscillatory.

Def i nition 1.2We say that functions Hi,i=1,2,belong to a function class H,if Hi∈C(D;[0,+∞)),i=1,2,satisfy

1.Hi(t,s)=0,i=1,2 for t=s, 2.Hi(t,s)＞0,i=1,2 for t＞s,

where D={(t,s)：0＜s≤t＜+∞}.Moreover,the partial derivatives?H1/?s and?H2/?s exist on D such that

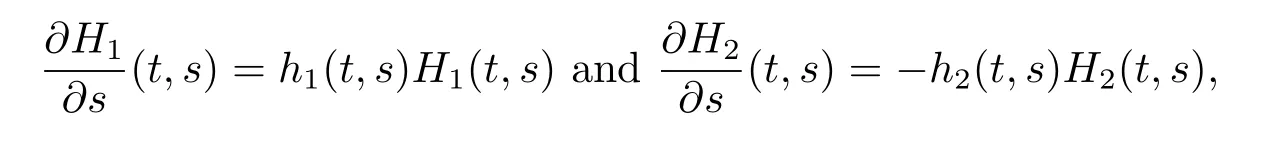
where h1,h2∈Cloc(D;R).

In recent years,there was much research activity concerning the oscillation theory of nonlinear hyperbolic equations with functional arguments by employing Riccati technique. Riccati techniques were used to obtain various oscillation results.Recently,Shoukaku and Yoshida[2]derived oscillation criteria by using oscillation criteria of Riccati inequality.In this work,we study the hyperbolic equation with impulsive.

2 Main Results

Theorem 2.1If for each T≥0,there exist(H1,H2)∈H and a,b,c∈R such that T≤a＜c＜b and

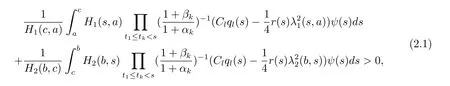
then every solution of the problems(1.1)-(1.4)oscillates in Ω,where

ProofSuppose to the contrary that there is a nonoscillatory solution u(x,t)of the problems(1.1)-(1.4).Without loss of generality we may assume that u(x,t)＞0 in G× [t0,+∞)for some t0＞0 because the case where u(x,t)＜0 can be treated similarly.Since (H2)holds,we see that u(x,τi(t))＞0(i=1,2,···n)in G×[t1,+∞)for some t1≥t0.

(1)For t≥t1,t 6=tk,k=1,2,···,integrating(1)with respect to x over G,we obtain

that is

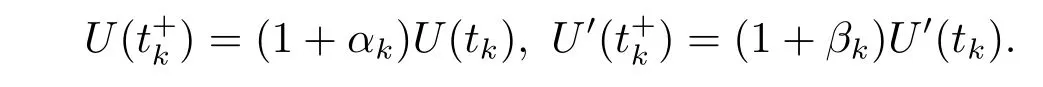
Thus we obtain that the functions U(t)is a eventually positive solution of the impulsive dif f erential inequality

Multiplying(2.4)by H2(t,s)and integrating over[c,t]for t∈[c,b),we have

which contradicts condition(2.1).

[1]Lakshmikantham V,Bainov D,Simeonov P S.Theory of impulsive dif f erential equations[M].Singapore：World Scientif i c,1989.

[2]Yutaka Shoukaku,Norio Yoshida.Oscillations of nonlinear hyperbolic equations with functional arguments via Riccati method[J].Appl.Math.Comput.,2010,217：143-151.

[3]Luo Zhiguo,Shen Jianhua.Oscillations of second linear dif f erential equations with impulses[J].Appl. Math.Lett.,2007,20：75-81.

[4]Bainov D D,Minchev E.Oscillation of the solutions of impulsive parabolic equations[J].J.Comput. Appl.Math.,1996,69：207-214.

[5]Liu Anping,Liu Ting,Zou Min.Oscillation of nonlinear impulsive parabolic dif f erential equations of neutral type[J].Rocky Mount.J.Math.,2011,41：833-850.

[6]Chen Rongsan,Zou Min,Liu Anping.Comparison of several numerical schemes for scalar linear advaction equation[J].J.Math.,2015,35(4)：977-982.

里卡蒂方法研究帶泛函參數(shù)的非線性脈沖時滯雙曲方程的振動性

鄒敏,陳榮三,劉安平

(中國地質(zhì)大學(xué)(武漢)數(shù)學(xué)與物理學(xué)院,湖北武漢430074)

本文研究了帶泛函參數(shù)的非線性脈沖時滯雙曲方程的振動性問題.利用積分平均法和里卡蒂方法得到了這類方程解的振動性的一個充分條件,對非線性時滯雙曲方程解的震動性進(jìn)行了推廣,能更好地利用一些現(xiàn)有的脈沖時滯常微分方程解的振動性的結(jié)論.

振動;脈沖;時滯;雙曲方程;Riccati不等式

O175.27

A

0255-7797(2017)05-1007-06

?Received date：2015-11-25Accepted date：2016-03-04

Supported by National Natural Science Foundation of China(11201436).

Biography：Zou min(1981-),female,born at Xiantao,Hubei,lecturer,major in partial dif f erential equation.

2010 MR Subject Classif i cation：58J45;35B05