張旭,吳嘎日迪

(內(nèi)蒙古師范大學數(shù)學科學學院,內(nèi)蒙古 呼和浩特 010022)

1 引言及主要結(jié)果

Rnl表示分母是次數(shù)不超過n的多項式,分子是線性函數(shù)的有理函數(shù)的全體,即

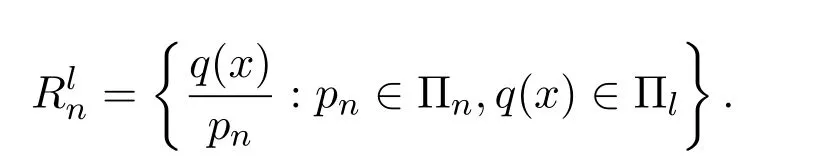
梅雪峰等在文獻[1]中研究了在Lp內(nèi)一類有理函數(shù)逼近的問題,所得結(jié)果如下：

定理 A[1]設(shè)l是自然數(shù),1＜p＜∞,如果f(x)∈Lp[?1,1]在 (?1,1)內(nèi)改變l次符號,則存在?1＜b1＜b2＜ ···＜bl＜1和使得

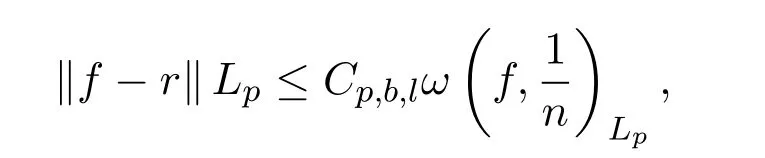
其中

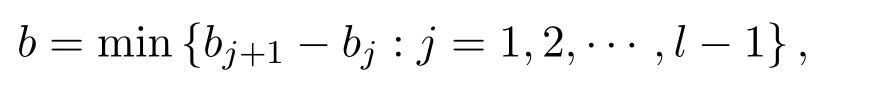
Cp,b,l表示與p,b,l有關(guān)的正常數(shù).

本文在Orlicz空間內(nèi)研究類似的有理函數(shù)逼近問題.

本文用M(u)和N(v)表示互余的N函數(shù),有關(guān)N函數(shù)的定義和性質(zhì)見文獻 [2].設(shè)L?M[?1,1]表示區(qū)間 [-1,1]上N函數(shù)M(u)生成的 Orlicz空間,‖·‖M是 Orlicz范數(shù),定義如下:

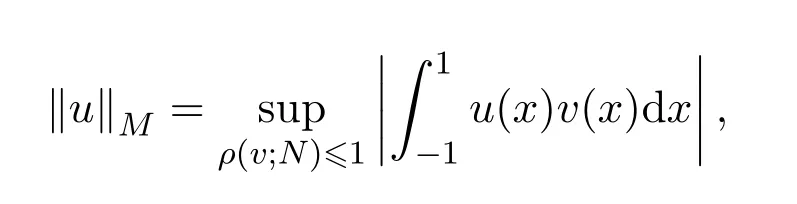
其中

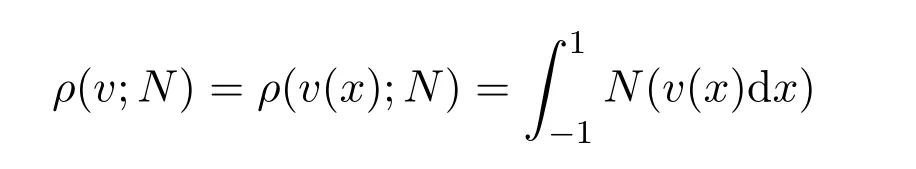
是v(x)關(guān)于N(v)的模.

對于f∈L?M[?1,1]和 0≤t≤1,定義連續(xù)模如下：

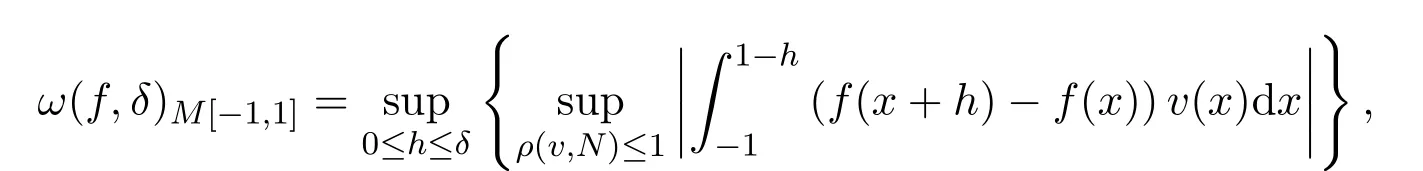
并記

定義 1.1[3]設(shè)f∈ L?M[?1,1],如果有l(wèi)個點?1＜a1＜ a2＜ ···＜ al＜1,使得

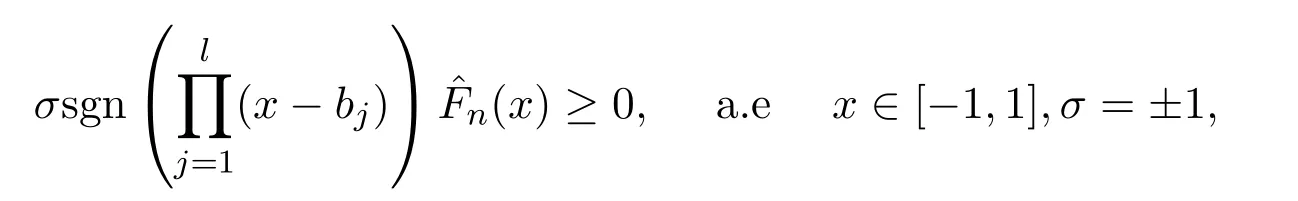
且對所有的j=1,2,···,l和 0＜ η ＜aj+1?aj(aj+1=1),

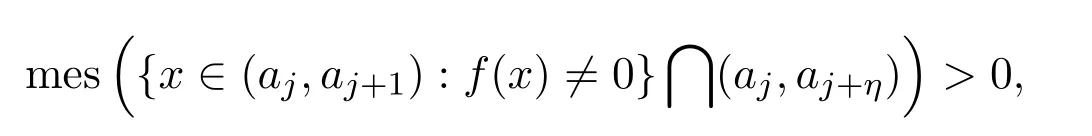
這里要求

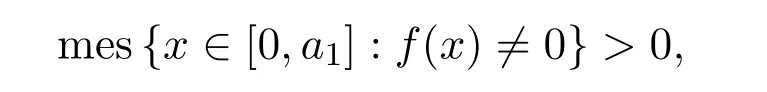
則說f(x)在點a1,a2,···,al處改變l次符號.

本文的主要結(jié)果如下：

定理 1.1設(shè)f(x)不恒等于 0,f(x)在 (?1,,1)內(nèi)恰好改變l次符號,則存在?1＜b1＜b2＜ ···＜bl＜1和使得

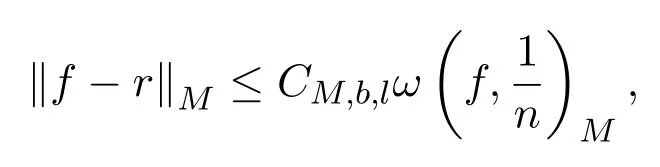
其中

CM,b,l表示與M,b,l有關(guān)的正常數(shù).在不同處表示不同的值.

2 若干引理

引理 2.1[4]設(shè)且f(x)延拓如下:

則

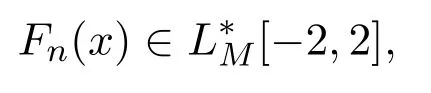
并且

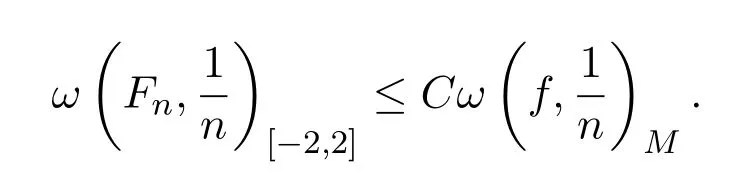
引理 2.2[5-6]設(shè)在 (?1,1)內(nèi)恰好改變l次符號.記

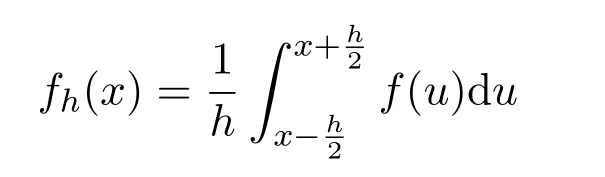
為f(x)的一階Steklov函數(shù),則對充分小的h＞0,fh(x)在區(qū)間內(nèi)恰好改變l次符號.

引理 2.3[4]設(shè)fh(x)為f(x)的一階 Steklov函數(shù),記

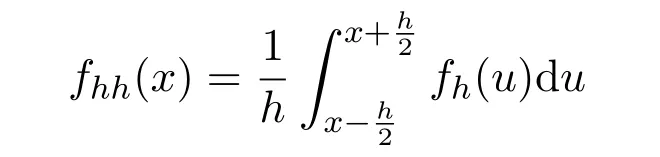
為f(x)的二階Steklov函數(shù),則對充分小的h＞0,有

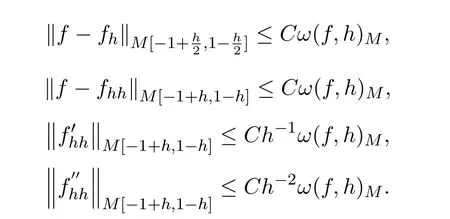
引理 2.4[3]定義修正的Jackson核如下:

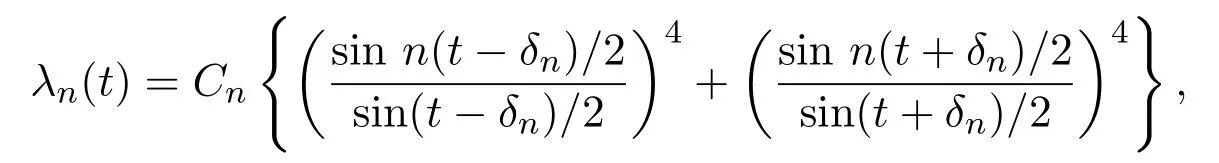
其中

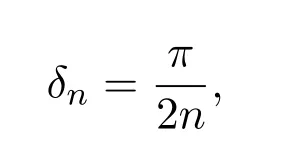
Cn滿足

對周期為 2π的可積函數(shù)f(x)(記)定義

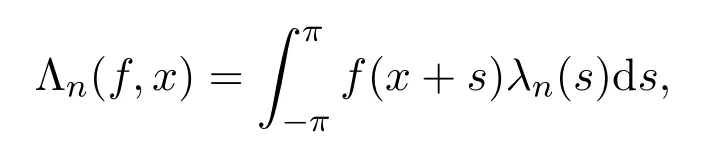
則

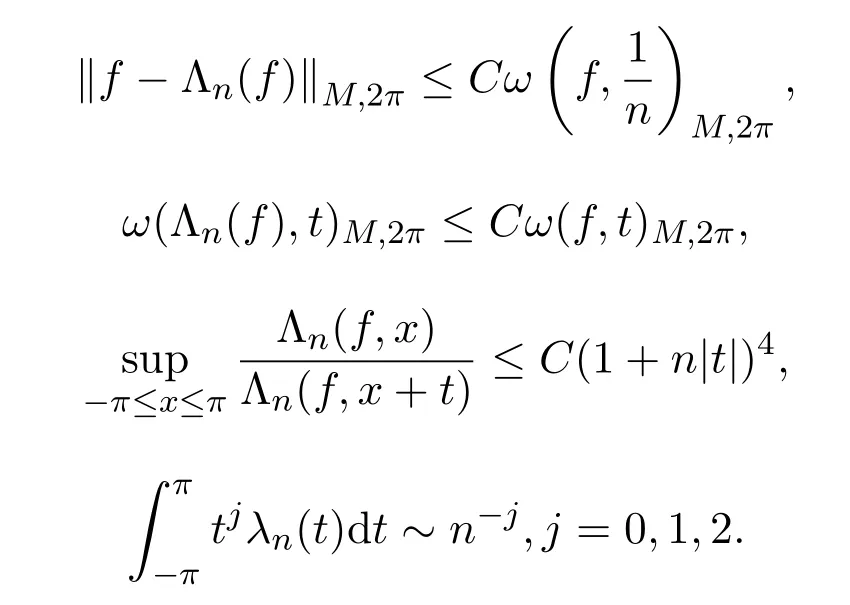
引理 2.5[7]設(shè),x∈I?[a,b],定義

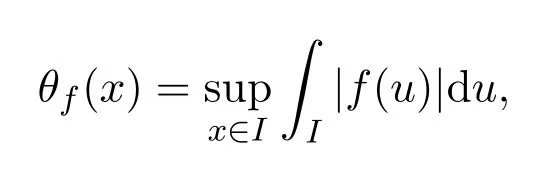
則

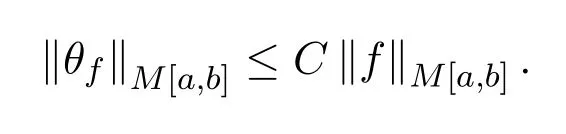
引理 2.6[1]令

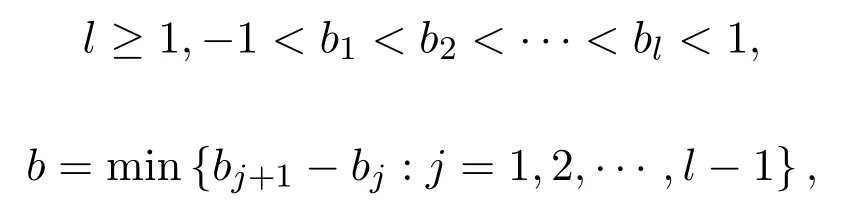
對于θ,s ∈[?π,π]和 cos(θ+s)≠bj,j=1,2,···,l,有

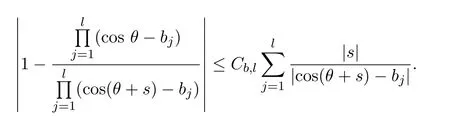
3 定理的證明

在下面的證明中,假設(shè)

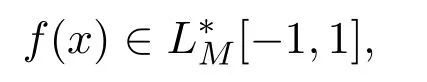
在區(qū)間 (?1,1)內(nèi)恰好改變l次符號,f(x)不恒等于 0.按引理 2.1的方式把f(x)∈L?M[?1,1]延拓成Fn(x)∈L?M[?2,2],顯然Fn(x)在區(qū)間 (?2,2)恰好改變l次符號,且滿足

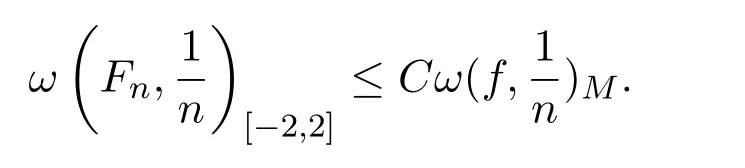
對x∈[?2,2],對充分小的h＞0,定義Fn(x)的二階Steklov函數(shù)即

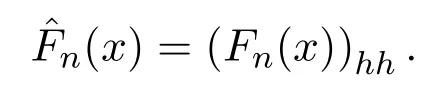
對應(yīng)于f(x)在(?1,1)內(nèi)的l次變號點對于給定的a1＜a2＜···＜al,在?1＜b1＜b2＜···＜bl＜1,這些點處改變符號.對于給定的ε＞0,

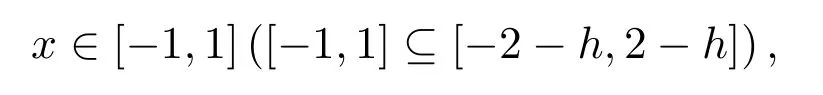
不妨設(shè)

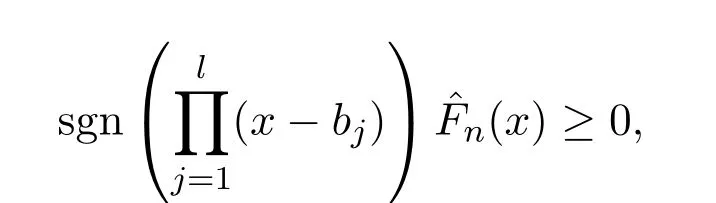
令

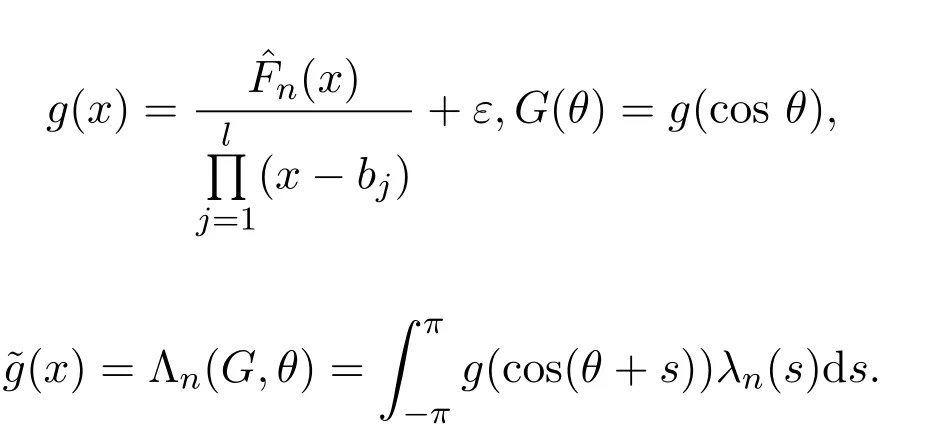
取通常意義下的Jackson核為:

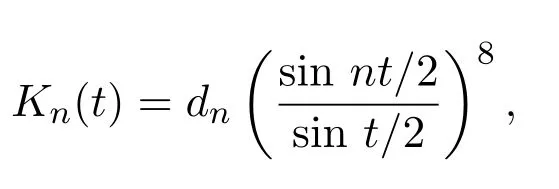
其中常數(shù)dn滿足

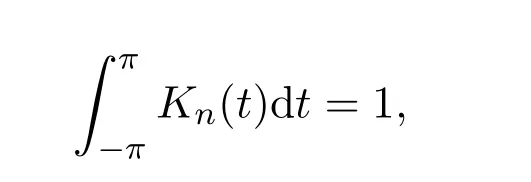
由文獻[8]可知dn～n?7,并且有

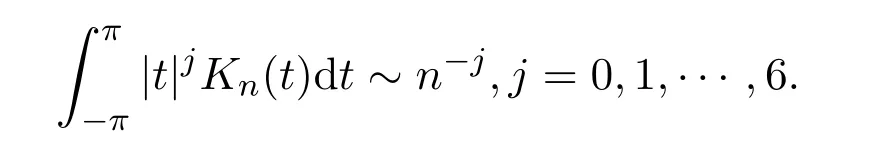
定義

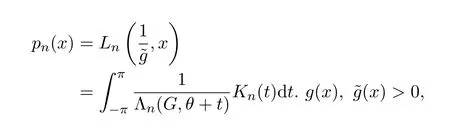
因此pn(x)的定義是合理的,且是一個n次多項式,在以下的證明中取

由引理2.1,引理2.3得

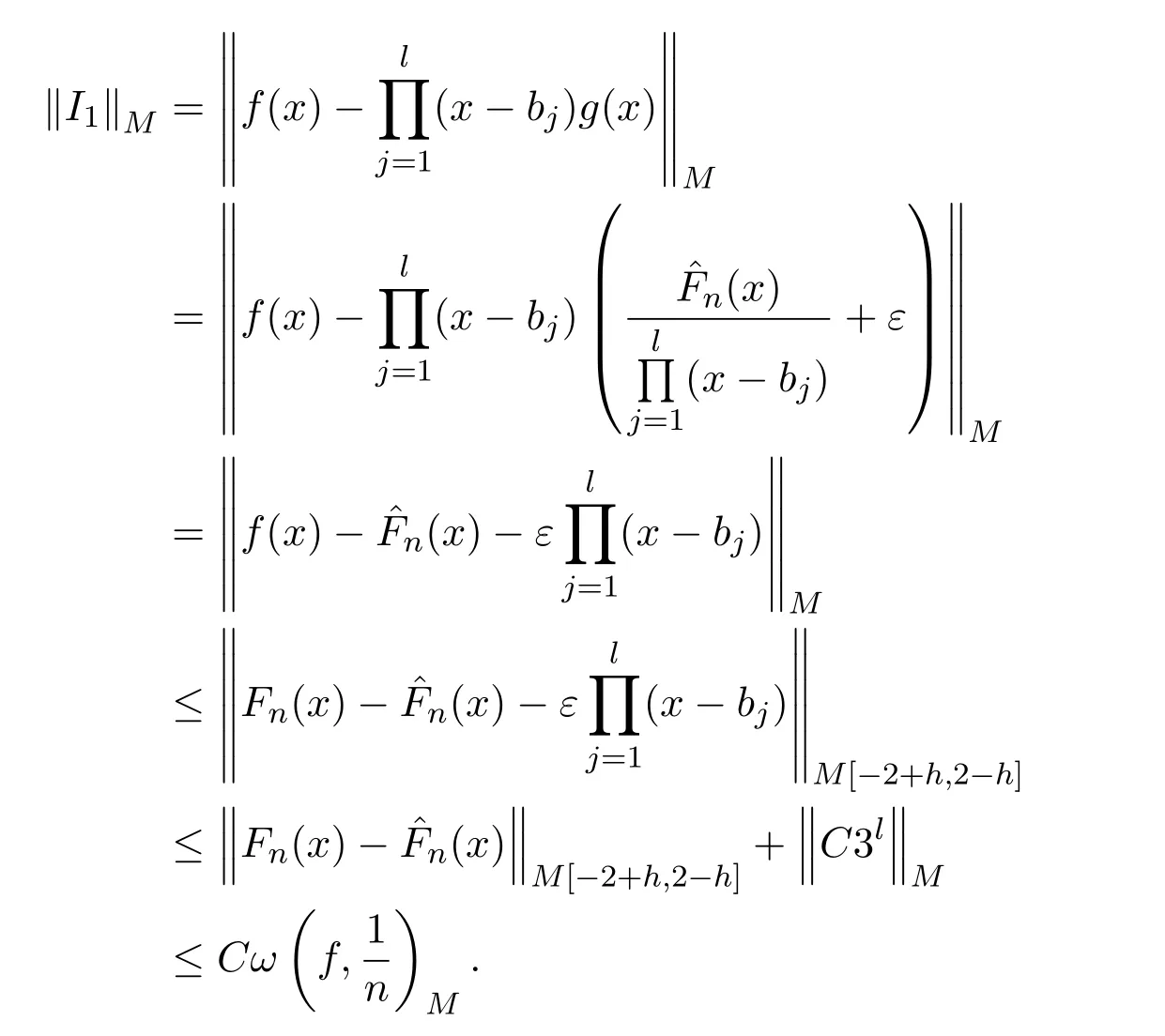
由文獻[1]知,

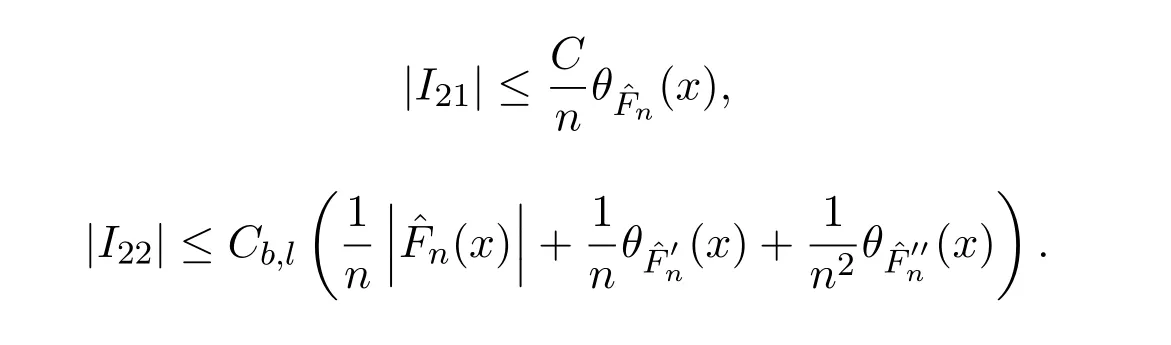
利用引理2.5,得

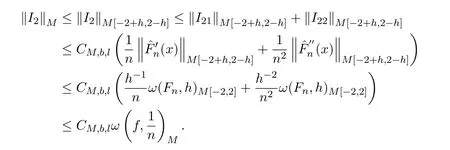
為了估計‖I3‖M,劃分區(qū)間如下:

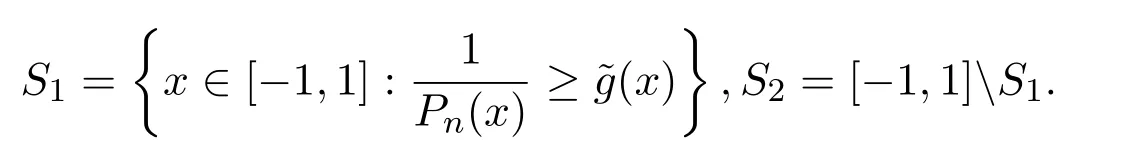
對x∈S1,有Cauchy-Schwarz不等式可知,

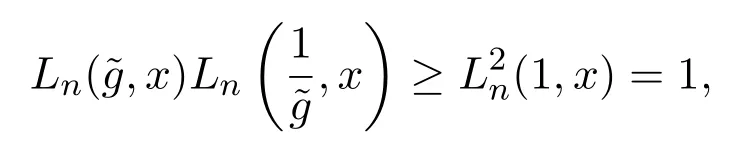
所以有

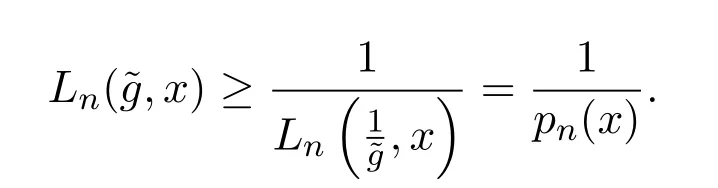
對x∈S1,則由文獻[1]得

注意到x=cosθ,由引理 2.3,引理 2.4,引理 2.5和

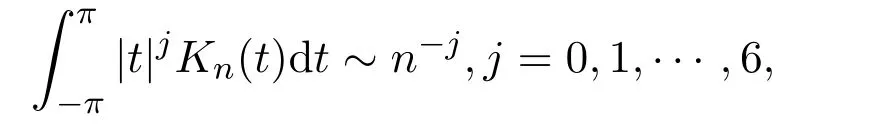
得

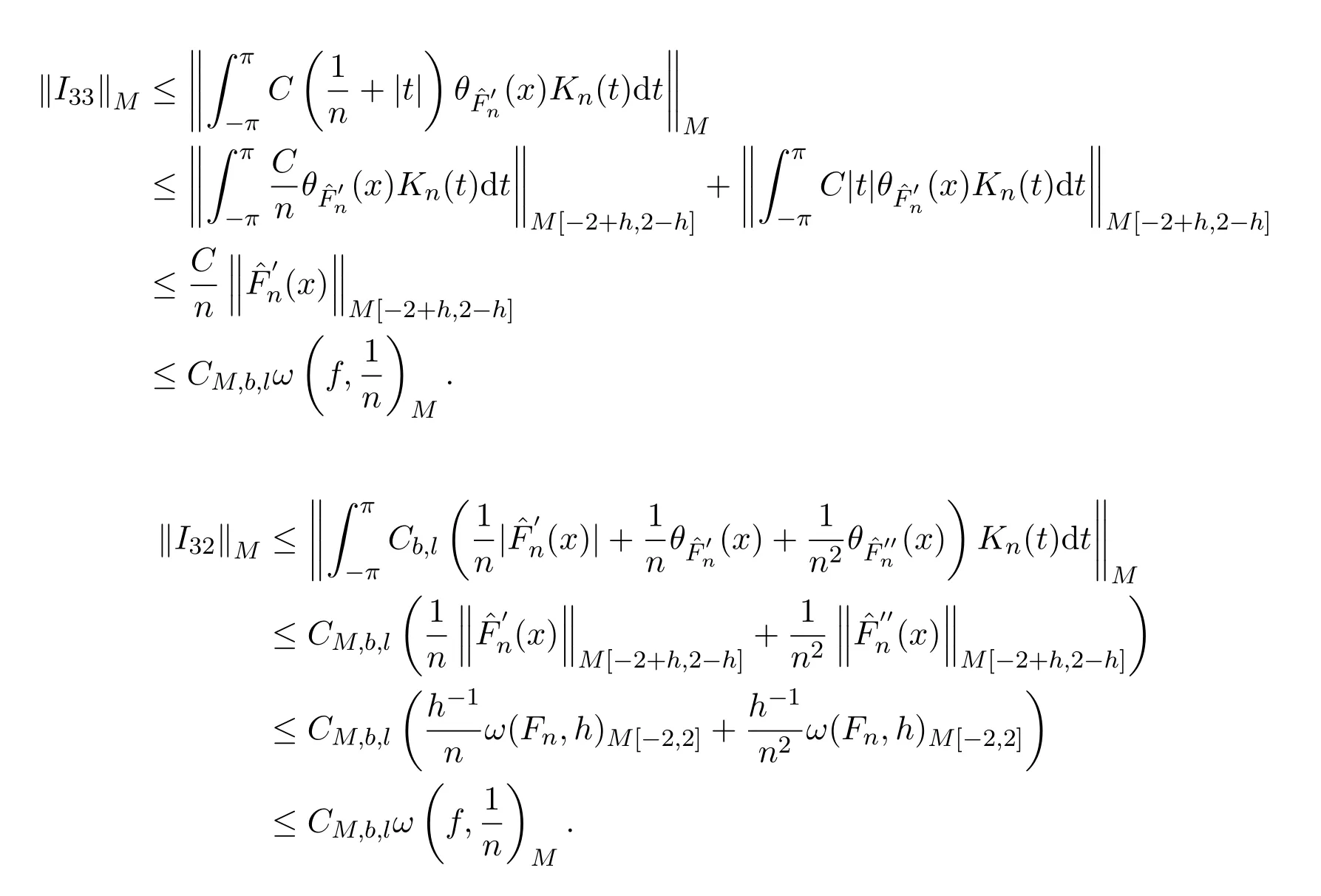
由引理2.6可得

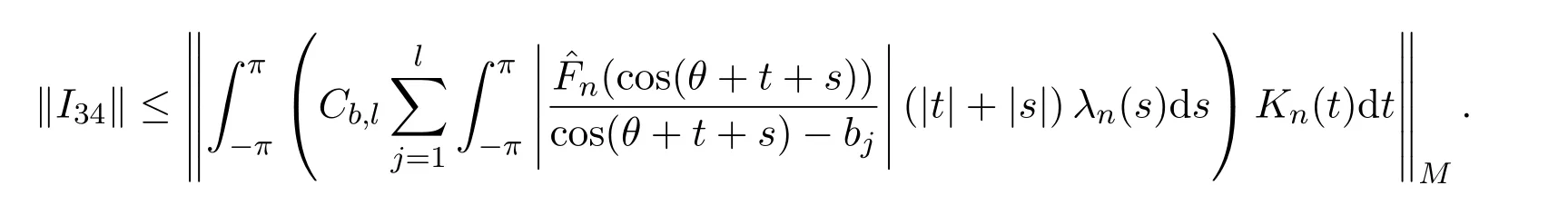
令j ∈ {1,2,···,l},并定義

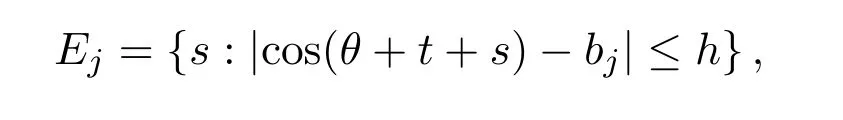
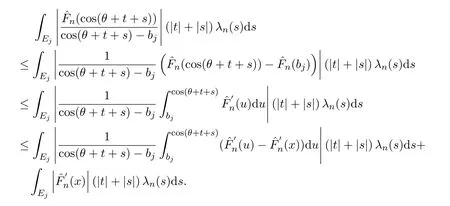
對任何x,u∈[?1,1],注意到x=cosθ,u位于 cos(θ+t+s)和bj之間,當s∈Ej時,

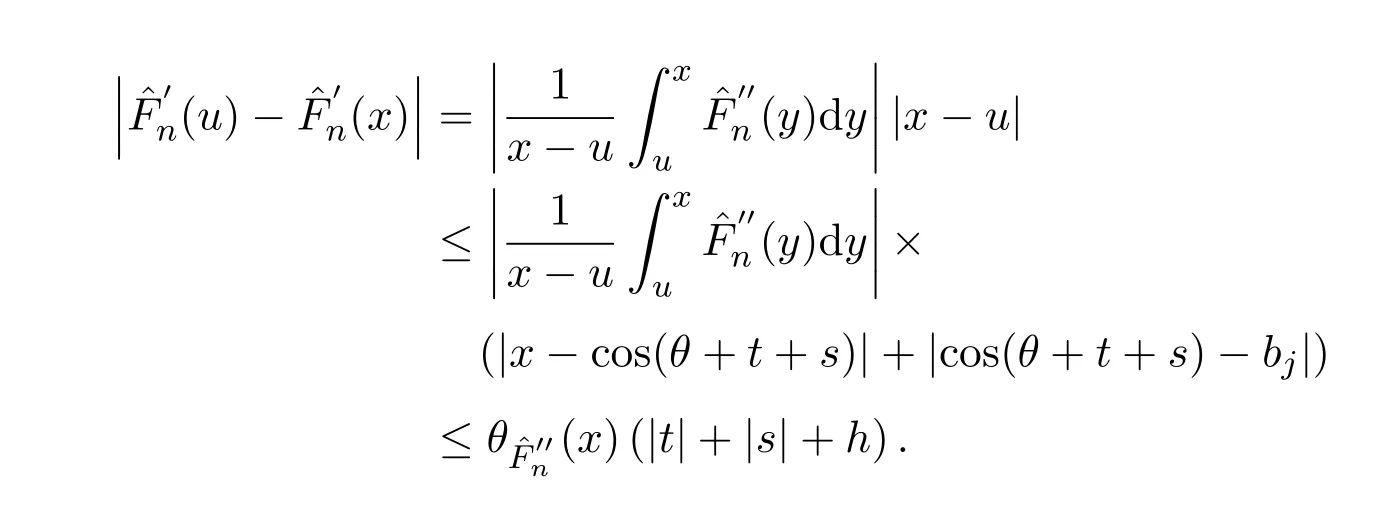
于是由引理2.4得

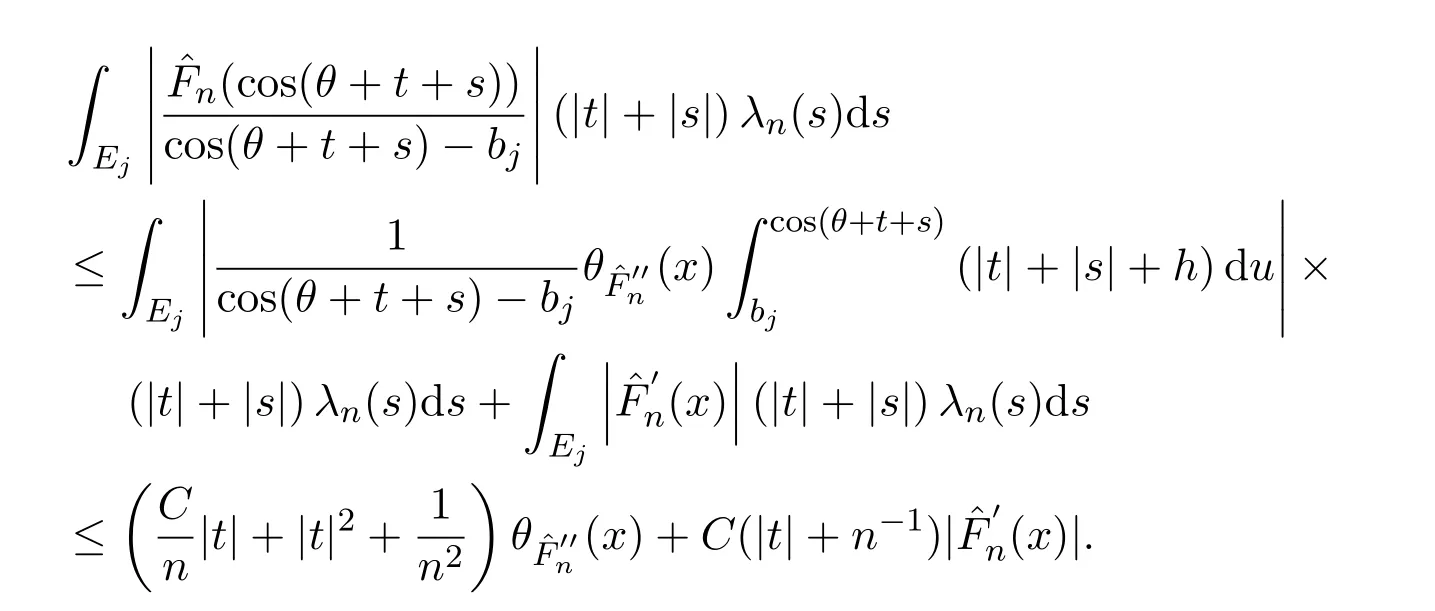
另一方面,當

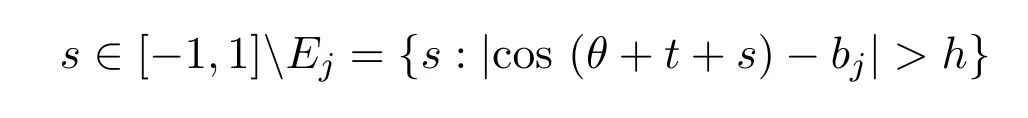
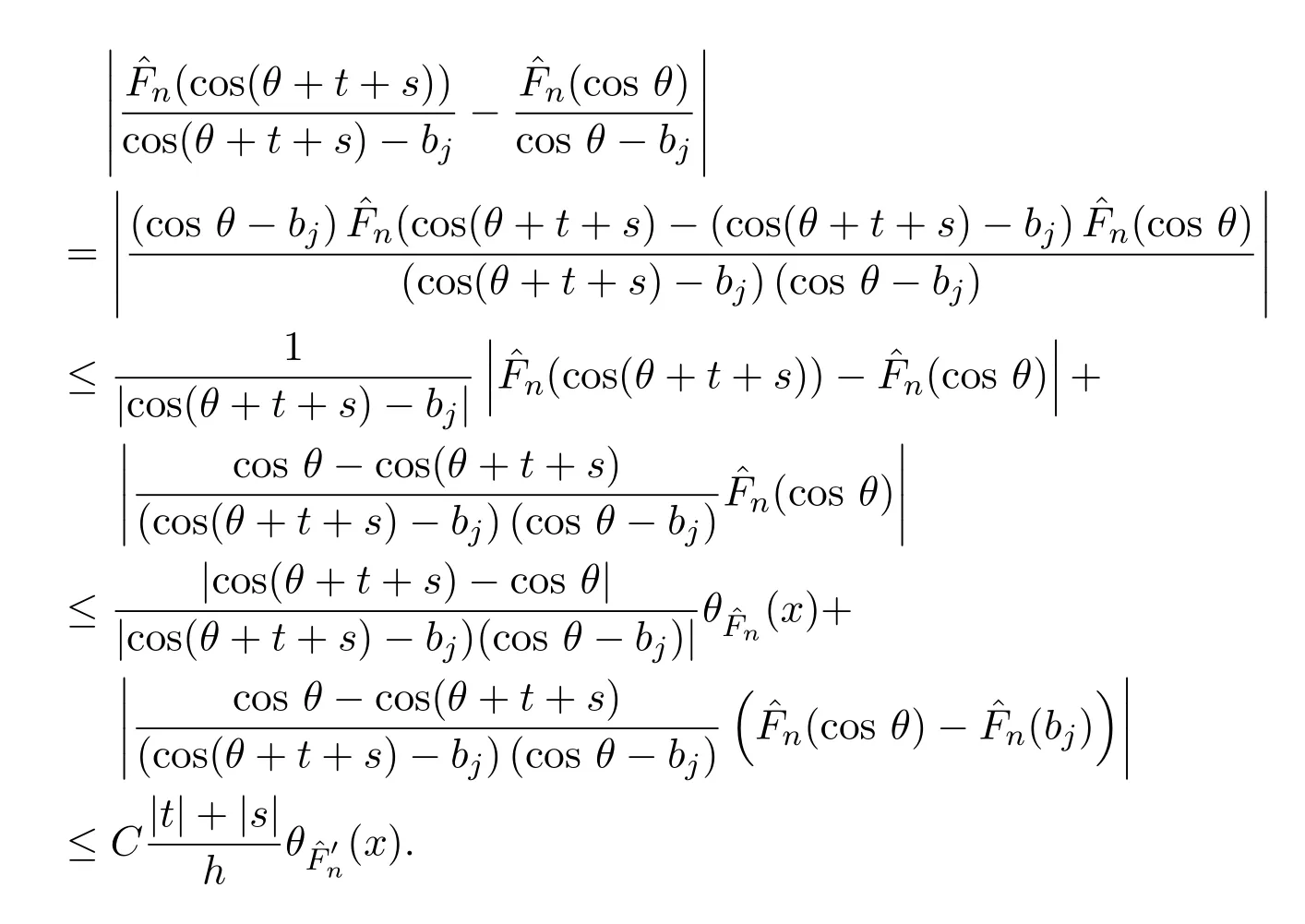
由引理2.5可得

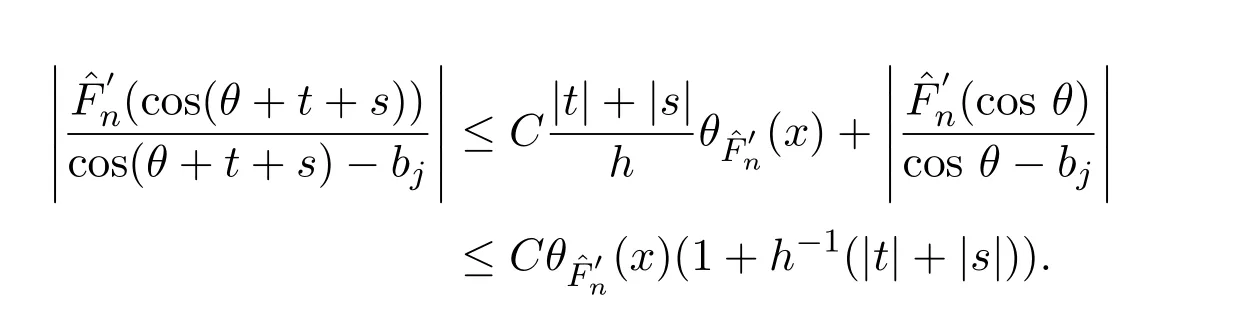
所以

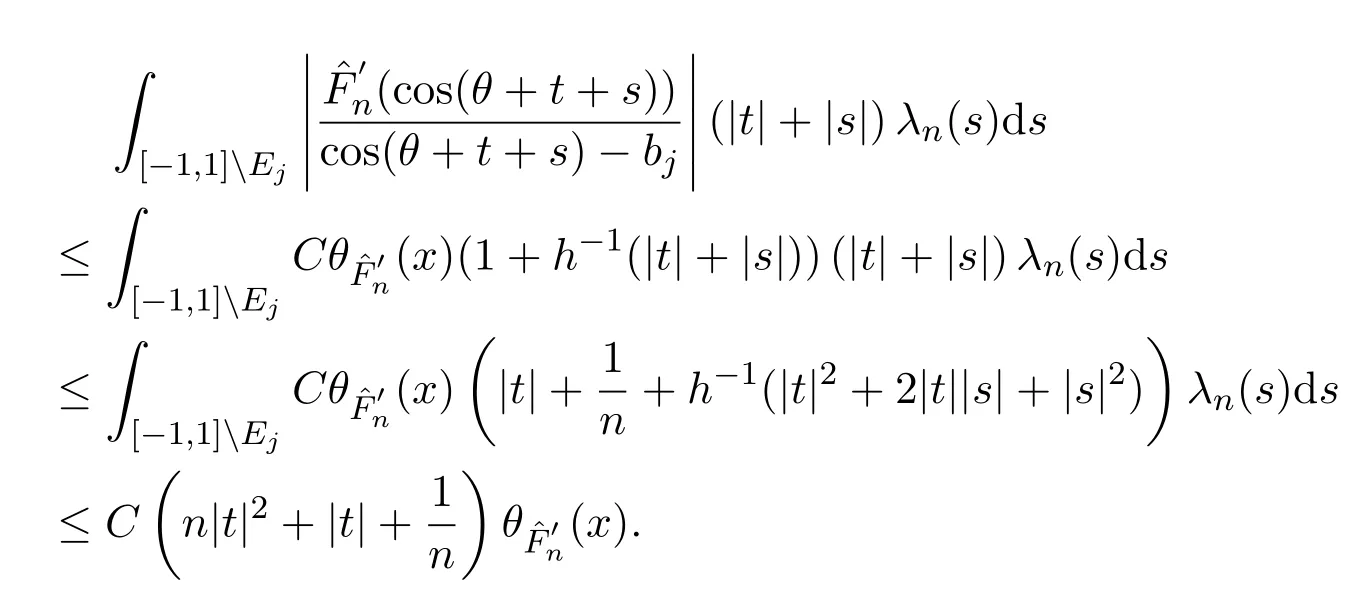
對于x∈[?1,1],有

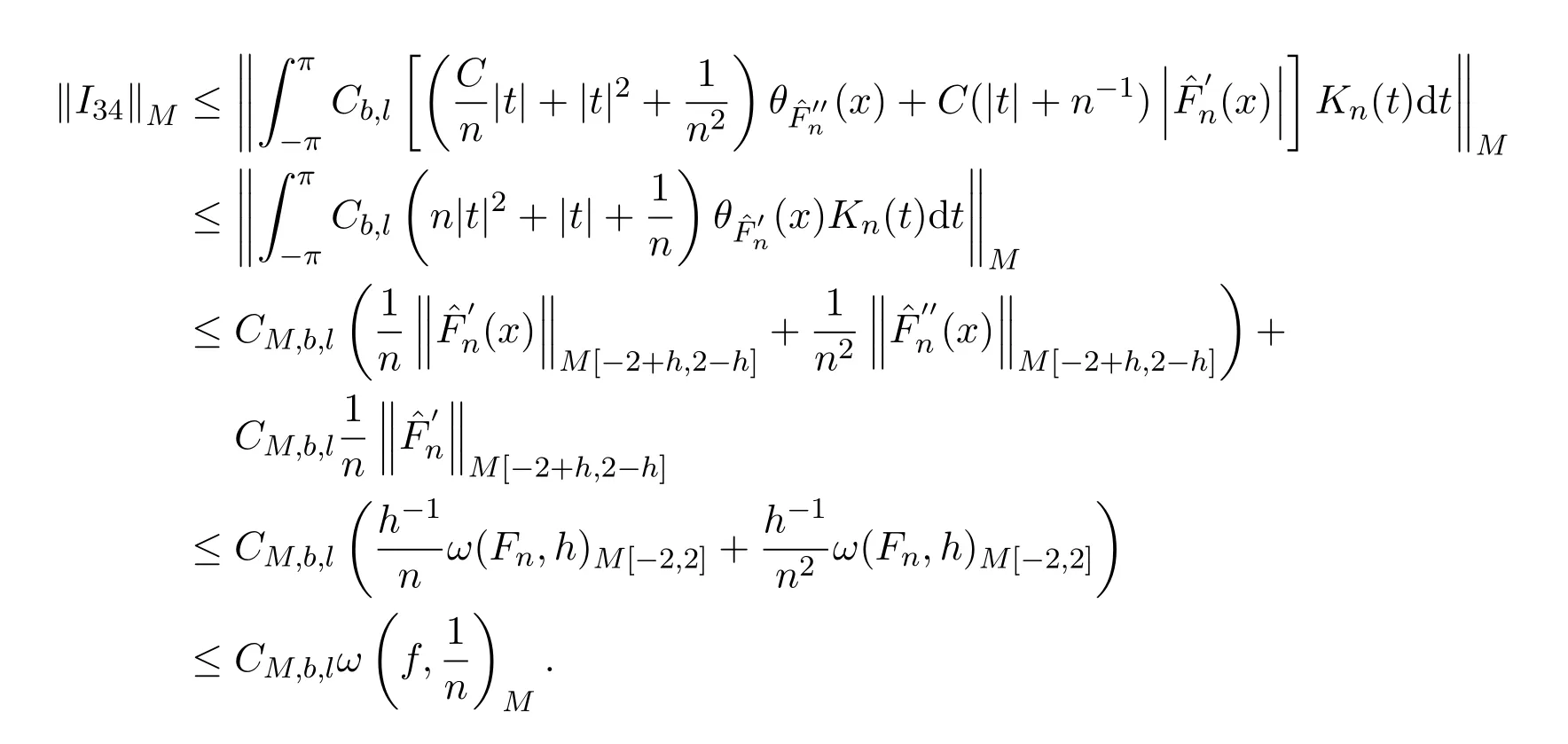
所以

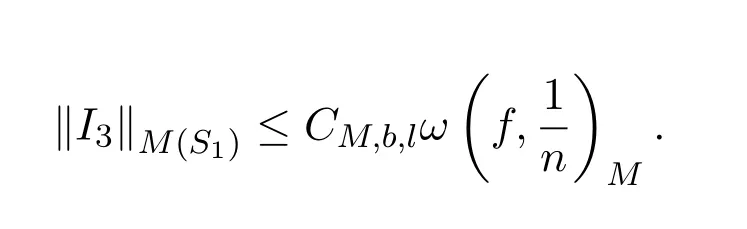
當x∈S2時,有

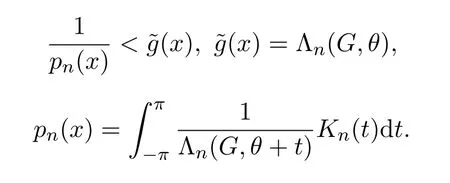
由引理2.4得

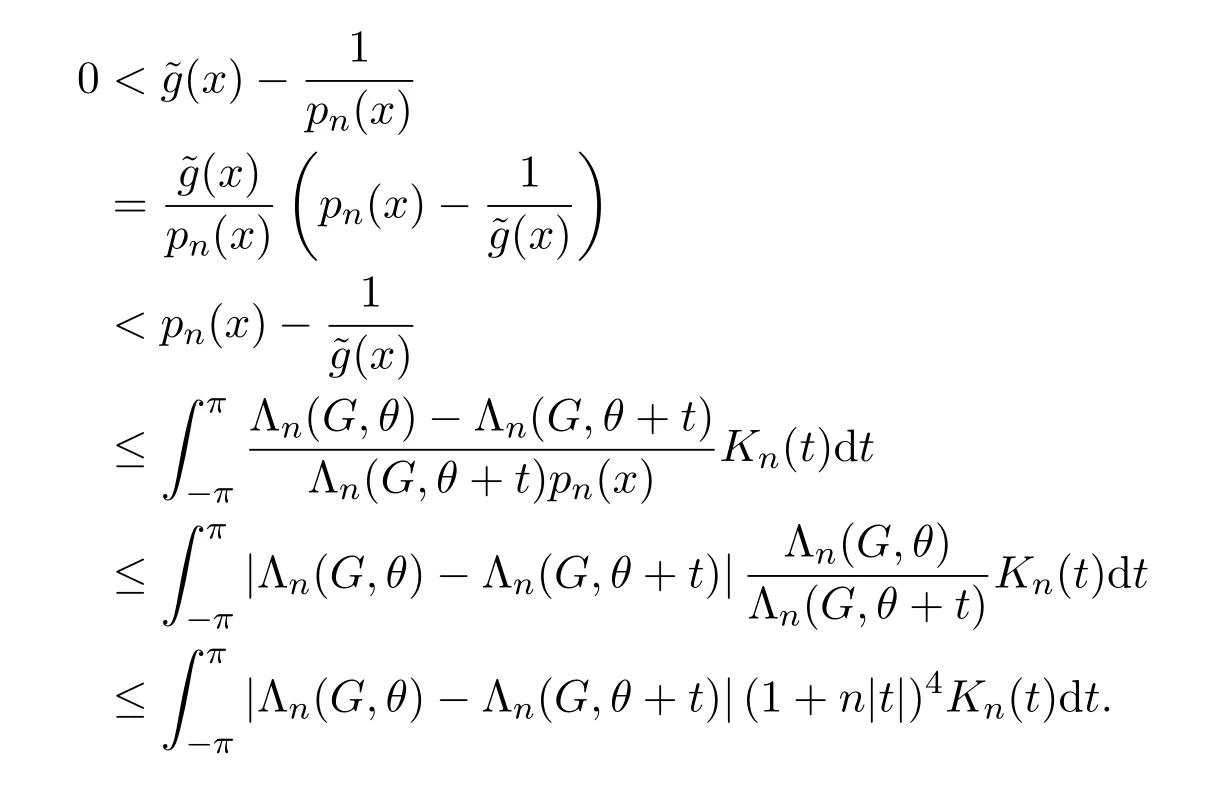
令

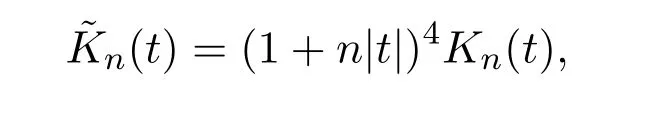
為x∈S2的Jackson核,當x∈S2,類似x∈S1的估計

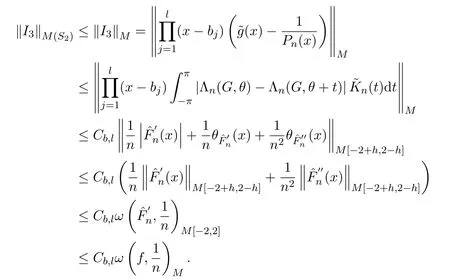
綜上所述,

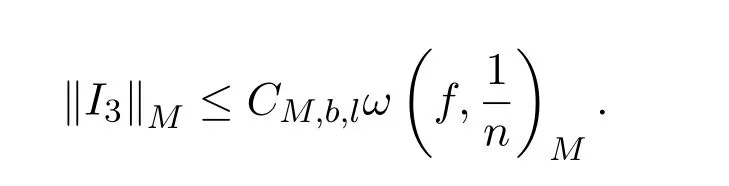
所以

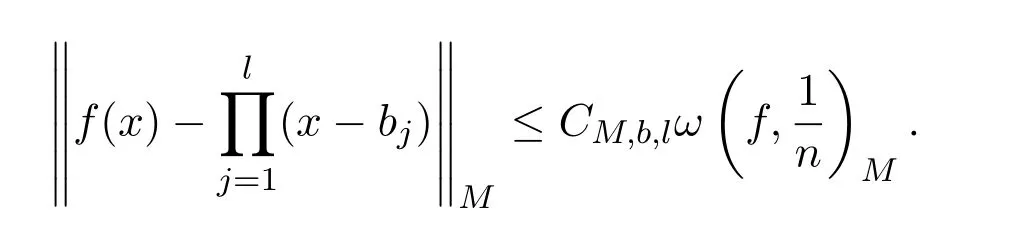
定理得證.

[1]Mei Xuefeng,Zhou Songping.Approximation by rational functions with prescirbed numerator degree inLpspaces for 1＜p＜∞[J].Acta Math.Hungar.,2004,102(4):321-336.

[2]吳從忻,王廷輔.奧爾里奇空間及其應(yīng)用[M].哈爾濱:黑龍江科學技術(shù)出版社,1983.

[3]Hai Lian,Wu Garidi.On approximation by reciprocals of polynomials with positive coefficients[J].Analysis in theory and Applications,2013,29(2):149-157.

[4]王曉芳.若干函數(shù)空間內(nèi)的幾個逼近問題[D].呼和浩特:內(nèi)蒙古師范大學數(shù)學科學學院,2006.

[5]Wu Garidi.On approximation by polynomials in Orlicz spaces[J].Approximation theory and its Applications,1991,7(3):97-110.

[6]Wang Xiaoli,Huo Ran,Wu Garidi.On approximation by reciprocals of polynomials with positive coefficients in Orlicz spaces[J].Analysis in theory and Applications,2008,24(4):364-376.

[7]吳嘎日迪.一類新型Kantorovich算子在Orlicz空間內(nèi)的逼近性質(zhì)[J].內(nèi)蒙古師范大學學報(自然科學中文版),2006,35(3):253-257.

[8]Lorentz G G,Approximation of Functions[M].New York:Holt Rinehart and Winston,1966.