JingYang＊,YiyunChengKostasP.Peppas,P.TakisMathiopoulos,JieDing

1 School of Information Engineering, Yangzhou University, Yangzhou 225009, China

2 Department of Telecommunication Science and Technology, University of Peloponnese, Tripoli 22100, Greece

3 Department of Informatics and Telecommunications, National and Kapodistrian University of Athens, Athens 157 84, Greece

I. INTRODUCTION

Cognitive relaying technology has recently emerged as an attractive wireless technology because of its ability to achieve higher spectral efficiency [1]. A key relaying technique for cooperative relaying systems is the so-called decode-and-forward (DF) protocol. In the DF protocol, the transmitter sends a signal to the relay node for decoding, and the relay node forwards the signal to the receiver after successful decoding has been performed.

The end-to-end outage probability (OP) is an important performance metric for cognitive relaying systems. Several past research works have addressed the OP performance of various cognitive relaying networks [2-6].For example, in [2], the exact OP of cognitive DF relaying networks has been studied for Rayleigh fading channels. In [3], an approximate expression and a lower bound for the OP have been presented, considering the mutual interference between the secondary and primary users. The OP of a cognitive DF relaying network operating over Nakagami-mfading channels has been presented in [4] and [5]. In[6], assuming that the secondary network selects theN-th best relay, the OP of a cognitive DF relay network operating over Nakagami-mfading channels has been analyzed. Recently,the incremental DF (IDF) has attracted the attention of the research community, since it can efficiently improve transmission reliability [7]. For the IDF protocol, the relay node relays the transmitter’s information to the destination only when the direct transmission is not successfully. The outage performance of cognitive IDF relaying networks in Rayleigh and Nakagami-mfading channels have been addressed in [8] and [9], respectively. In [10],the OP has been studied for multiple IDF relay nodes applications. Another important wireless transmission technique, the so-called simultaneous wireless information and power transfer (SWIPT) has been proposed as an efficient means of prolonging system lifetime and achieving higher energy efficiencies [11].Power slitting (PS) and time switching (TS)protocols are the two popular protocols used in conjunction with SWIPT systems [11, 12].Considering a PS cooperative relaying system,the relay node divides the received power into two parts, i.e., information processing and energy collection. For the TS scheme, the relay node periodically switches in time between energy harvesting and information processing.

Several research works addressing the performance of SWIPT systems are available in the open technical literature [12-20]. For example, in [12], several SWIPT schemes have been investigated, assuming different network structures with single and multiple users. Considering multiple-input multiple-output (MIMO) interference networks,[15] has presented techniques which minimize the total transmit power by jointly designing the transmit precoders, receive filters and PS ratios under a predefined signal-to-interference-plus-noise ratio (SINR) and EH constraints. In [16], the authors proposed a wireless energy harvesting protocol for a cognitive relaying network. In [18], an analytical expression for the OP and the rate-energy trade off between the ergodic capacity and harvested energy of cognitive AF relaying networks with PS protocol have been derived.In [19], the OP performance of the cognitive DF relaying network with SWIPT has been assessed. In [21], the optimization of the PS ratios at the relays are investigated for both DF and amplify-and-forward (AF) relaying protocols. In [22], the throughput for point-topoint wireless communication networks with energy harvesting constraints at the transmitter has been obtained. It is noted that all the above previously mentioned papers dealing with the subject of cognitive relaying networks with SWIPT, have considered operation in Rayleigh fading channels.

In this paper, the OP performance of cognitive relaying systems,have been investigated, employing SWIPT technology and operating over i.n.i.d.Nakagami-m fading channels.

Motivated by the above observations, here we consider the Nakagami-mdistribution which is a more versatile fading model that well describes propagation in a wireless fading environment. In particular, we derive exact analytical expressions for the OP performance of the cognitive relaying networks employing DF and IDF protocols. Analytical performance evaluation results, which have been verified by computer simulations, have shown that the OP performance of cognitive IDF relaying networks outperform their counterparts incognitive DF relaying networks which do not employ the direct link. These results can be conveniently used for the accurate assessment of the OP performance in the cognitive DF and IDF relaying network.

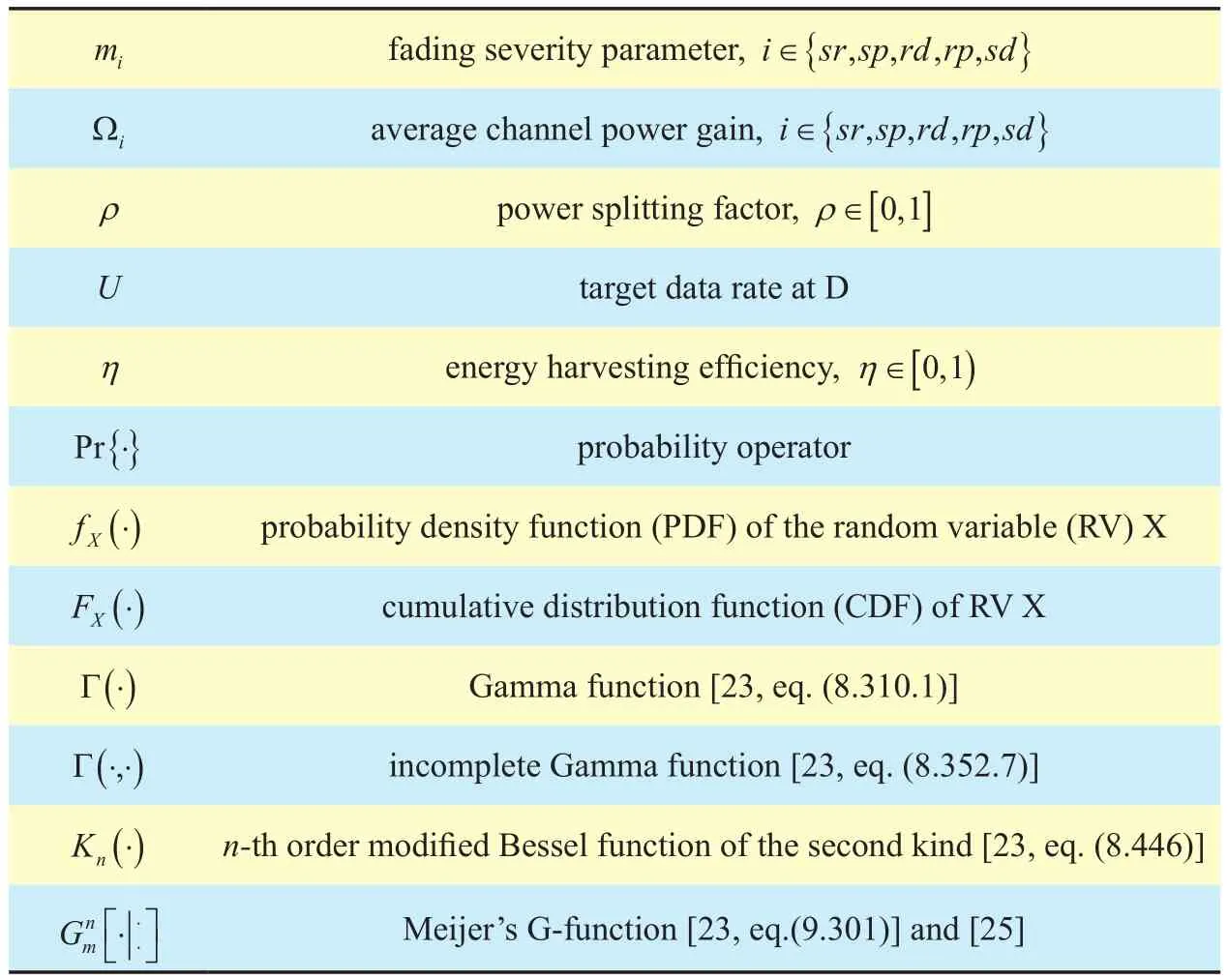
Table I. System parameters, mathematical operators and functions.

The remainder of this paper is organized as follows: Section 2 elaborates on the system model. Section 3 studies the OP performance of the cognitive relaying network operating under Nakagami-mfading. Numerical and computer simulation results are presented in Section 4. The conclusions of the paper can be found in Section 5.

II. SYSTEM MODEL

As illustrated in figure 1, we consider a cognitive DF relaying network consisting of a primary user (PU), a secondary transmitter (S),a secondary receiver (D) and an energy harvesting (EH) relay (R). The S communicates with D via the relay node R, in the presence of a PU. Since there is no energy supply for R, it needs to harvest energy from the transmitted signal of the S to forward the S’s information to D. In order to guarantee the quality of service (QoS) of the PU, the transmit power at S and R are constrained by the maximum tolerable interference power at PU and the maximum transmit power. It is assumed that a direct link between S and D exists, and the relay node employs the IDF protocol to process information.

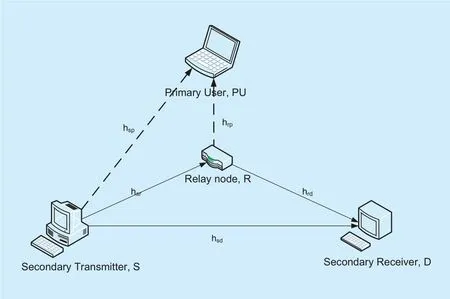
Fig. 1. System model con figuration of the cognitive DF relaying network under consideration.

The channel fading coefficients in S→PU and R→PU links are denoted ashspandhrp,respectively, while the channel coefficients in S→R, R→D and S→D are denoted ashsr,hrdandhsd, respectively. All channel coefficients are assumed to be independent but non-identically (i.n.i.d.) Nakagami-mrandom variables(RVs). The additive white Gaussian noise(AWGN) at R and D is represented asnRandnD, followingCN(0,1). Thus, the probability density function (PDF) and cumulative distribution function (CDF) of the channel gains X,whereare given as

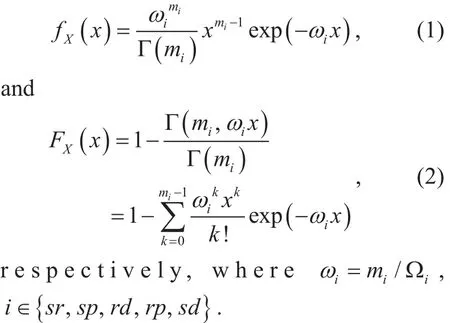
LetIandP0denote the maximum tolerable interference power at the PU and the maximum transmit power at S, respectively. Then, the transmit power at S, i.e.,PS, is constrained as

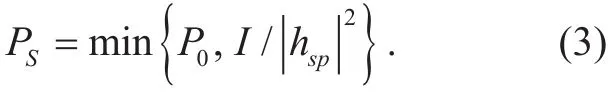
Let us consider the IDF, for which if the channel condition in the link between S and D is acceptable, S communicates directly with node D; otherwise, the information is transmitted via the EH relay node R [9].

For the first case, there is no outage in the S-D link, so that node S transmits the information signal directly to node D. The received signal at D can be expressed as

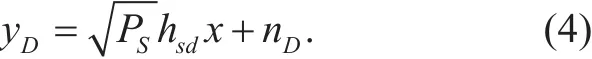
For the second case, the S-D link is in outage, so that S transmits the information signal to D via R. The communication between S and D takes place in two phases. During the first phase, S transmits its signalxto R, and after harvesting energy, the received signal at R can be expressed as

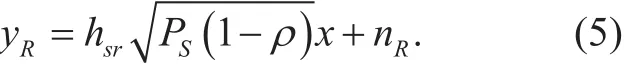
For successful signal detection at R, the following condition should be satis fi ed [19]

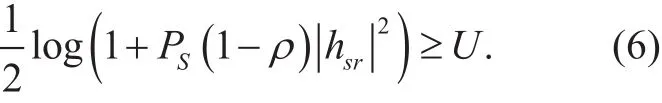
After energy harvesting, the power at R is given aswhereis the optimal power-splitting factor [19], whereε=22U?1.Note thatPrcan be expressed as [19]

During the second phase, R forwards the detected signal to D. Considering the maximum tolerable interference power constraintIat PU and the maximum transmit powerProf node R, the transmit power at R is given by

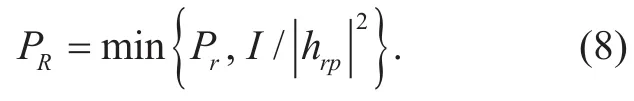
Therefore, the received signal at D can be expressed as

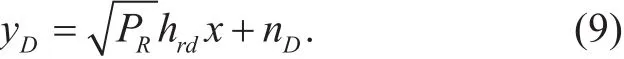
III. OUTAGE PERFORMANCE ANALYSIS

OP is defined as the probability that the link capacity between S and D does not exceed the target data rateU. In this section, we first derive the OP expressions of the cognitive IDF relaying network (see Section 3.1). In order to make a fair comparison, we also present in section 3.2 equivalent OP expressions for the cognitive DF relaying network, i.e., R always helps the transmission between S and D, when a acceptable communication link between S and D does not exist.

3.1 OP with the IDF protocol

We present the following Lemma 1 which lays the foundation for obtaining a closed-form OP expression, using semi-infinite integrals involving exponentials and modified Bessel functions of the second kind.

Lemma 1For any real number

ProofBy expressing the exponential and the Bessel functions as a Mellin-Barnes integral [24, eq. (8.4.3.1), eq. (8.4.23.1)], one obtains

The OP at D of the considered cognitive IDF relaying network can be obtained using the following theorem.

Theorem 1For the considered cognitive IDF relaying network employing SWIPT, the closed-form expression on the OP at the node D over i.n.i.d. Nakagami-mfading channel can be derived as

where P1and P2are given by (17) and (18),respectively, shown at the bottom of this page.

ProofSee Appendix A.

It should be noted that the result in (16) is expressed in closed-form in terms of the bivariate Meijer’s G-function whose efficient numerical implementation can be found in [26,27]. Furthermore, the Meijer’s G-function is included as standard built-in function in most popular mathematical software packages, such as MATHEMATICA and MATLAB.

3.2 OP with the DF Protocol

For comparison purposes, the performance of a cognitive relaying network in the conventional DF protocol without direct link between S and D will be considered here. In this case,the OP at D can be obtained through the following theorem.

Theorem 2With the conventional DF protocol, i.e., when there is no direct communication between S and D and the EH node R always helps the transmission between S and D, the OP at D over i.n.i.d. Nakagami-mfading channel can be mathematically expressed as (20) shown below.

ProofFor the conventional DF protocol,since there is no direct link between S and D,the EH node R always helps the transmission between S and D. Thus, the OP at D is expressed as follows [19],

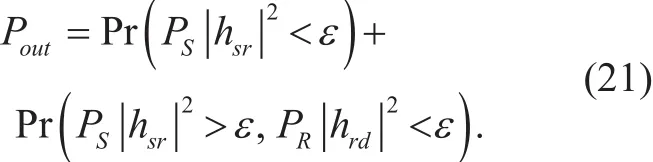
Substituting (3) and (8) into (21), the OP at D can be written as (22) at the bottom of this page.

Furthermore,Q1can be re-expressed as

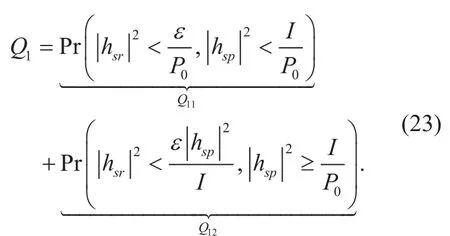
Since all links follow i.n.i.d. Nakagami-mfading, from (1) and (2), one obtains

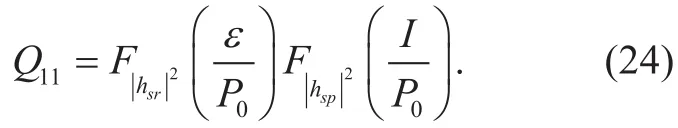
By employing [23, eq. (3.351.2)],Q12in(23) can be expressed as

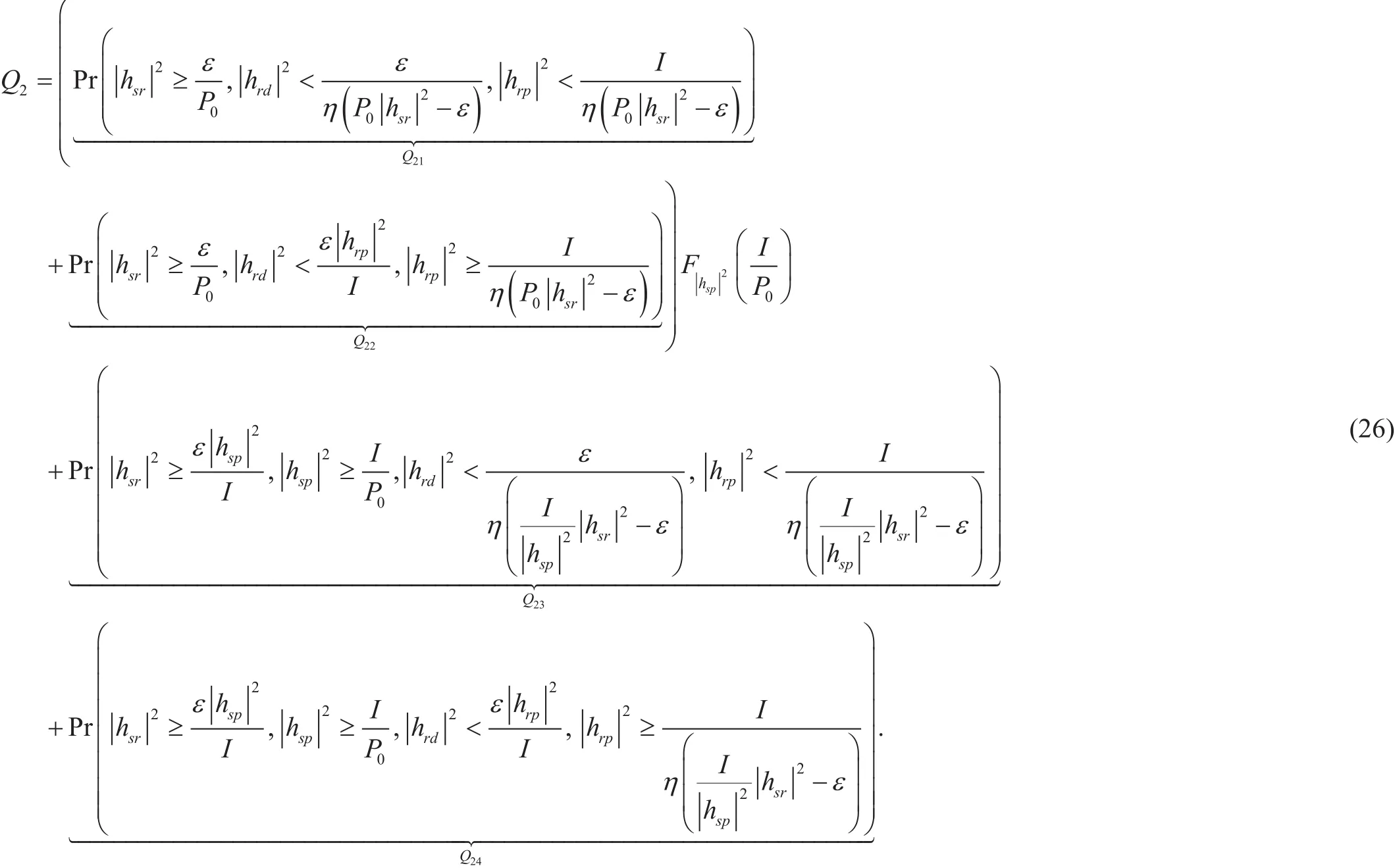
Substituting (24) and (25) into (23),Q1can readily deduced. Recalling (3) and (7),Q2in(22) can be re-written as in (26) whereQ21is given by (27) at next page.

By employing [23, eq. (1.110)], [23, eq.(3.351.3)], [23, eq. (3.471.9)] as well as the variable substitutionand Lemma 1,Q21can be obtained in a straightforward fashion. However, due to space limitations, this expression will not be presented here.

In a similar manner, the following expression forQ22can be obtained as in (28) shown at next page.

Furthermore,Q23can be expressed as (29)at the next page.

By employing the change of variablesand [23, eq. (1.111)], [23, eq.(3.351.2)], [23, eq. (3.471.9)] and Lemma 1,Q23can be readily deduced. Similar toQ23, an analytical expression forQ24can be expressed as (30) at the next page.

Substituting the results of (27)-(30) into(26) and after some straight-forward simpli-fications,Q2is readily obtained which concludes the proof.

It is noted that for the special case of Rayleigh fading channels, i.e.,it can be verified that (20) reduces to the previously known result [19, eq. (7)]. However, we note that the result in [19, eq. (7)] contains an integral,while we obtain the OP expression in closedform by utilizing Lemma 1.

IV. PERFORMANCE EVALUATION RESULTS AND DISCUSSION

In this section, various analytical performance evaluation results obtained using Eqs. (17)-(19),accompanied with equivalent computer simulated results obtained by Monte-Carlo simulations are presented. Without loss of generality, we have considered the following speci fi c values for the various system parameters: i) In figures 2-4,it is assumed thatandii) In figure 2 and 3, it is assumed thatAll the obtained OP performance evaluation results are plotted as a function of the average channel power gain of the main link, i.e.,From the results presented in Figs. 2-4, it can be clearly observed that all numerically evaluated results match very well with the equivalent ones obtained using Monte-Carlo simulations, which verifies the correctness of our proposed mathematical analysis.

Figure 2 depicts the OP of cognitive relaying networks with IDF and DF protocols,respectively, for different maximum tolerable interference powerI, and target data ratesU,withandη=0.5. As it can be observed, the OP performance improves for both protocols asIincreases, since less stringent power constraint is put at node S. However,the OP performance degrades asUincreases.Moreover, it can also be seen that at high SNR values, the OP performance with IDF protocol improves more as compared to the DF protocol.

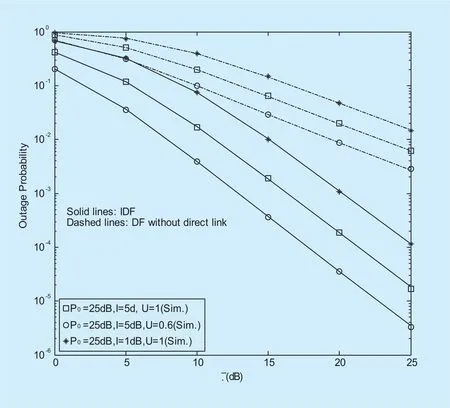
Fig. 2. Effects of the interference threshold I and targeted data rates U on the OP performance of the considered cognitive relaying system with SWIPT.

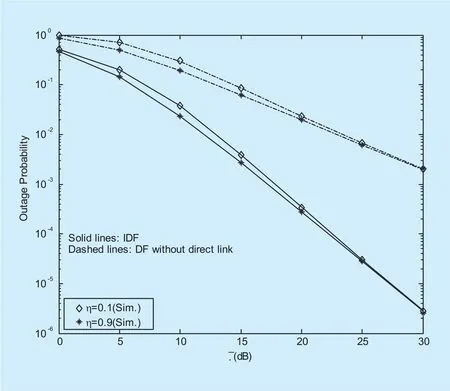
Fig. 3. Effects of the energy conversion ef fi ciency η on the OP performance of the considered cognitive relaying system with SWIPT,

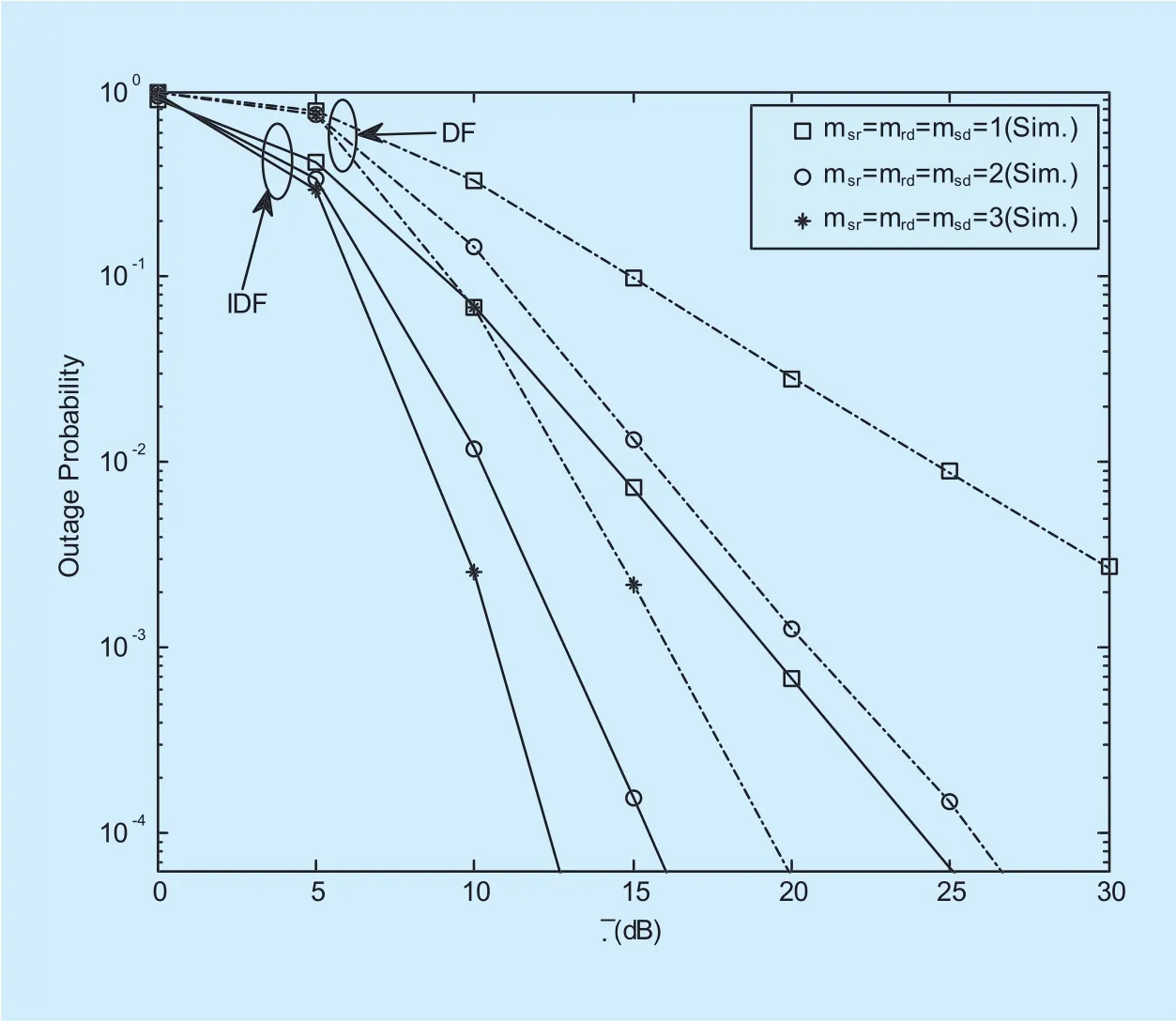
Fig. 4. OP of the cooperative cognitive relay system over Nakagami-m fading channel with different fading paraments.

Figure 3 depicts the effect of energy harvesting efficiency η on the OP for the cognitive relaying networks with IDF and DF protocols, assumingP0=10dB,I=5dB andU=1b/s/HZ. It can be observed that OP performance improves as η increases and the diversity gain in the IDF protocol is larger than that in the DF protocol.

Figure 4 illustrates the impact of the fading coefficient on the OP performance. Three cases are considered, i.e.,assumingP0=1dB,I=10dB,U=1b/s/HZ andη=0.5. As expected, the OP performance and diversity gains improve as the fading coef fi cients increase for both protocols.

V. CONCLUSIONS

In this paper, the OP performance of cognitive relaying systems, have been investigated, employing SWIPT technology and operating over i.n.i.d. Nakagami-mfading channels. Closedform analytical expressions on the OP of the cognitive relaying networks with IDF and the DF protocols have been derived, respectively,in terms of the bivariate Meijer’s G-function.All analytical results have been verified by equivalent performance results obtained by means of Monte-Carlo simulations. These results have shown that the OP performance in the cognitive relaying network with the IDF protocol outperforms its counterpart in the conventional DF protocol.

VI. Appendix A

The OP at D is expressed as follows,

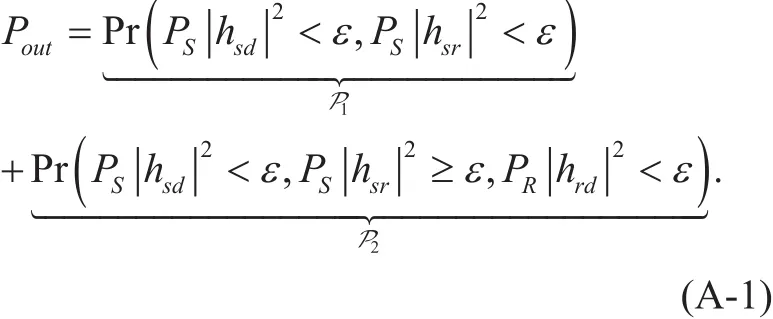
Substituting (3) and (8) into (A-1), the OP of the cognitive IDF relaying system with SWIPT can be expressed aswhere

Since all links follow i.n.i.d. Nakagami-mfading, from (1) and (2), one obtains

Substituting (1) and (2) into (A-5), and employing [23, eq. (3.351.2)],A12is finally deduced.

Recalling (3) and (7),P2in (A-1) is given as (A-6),

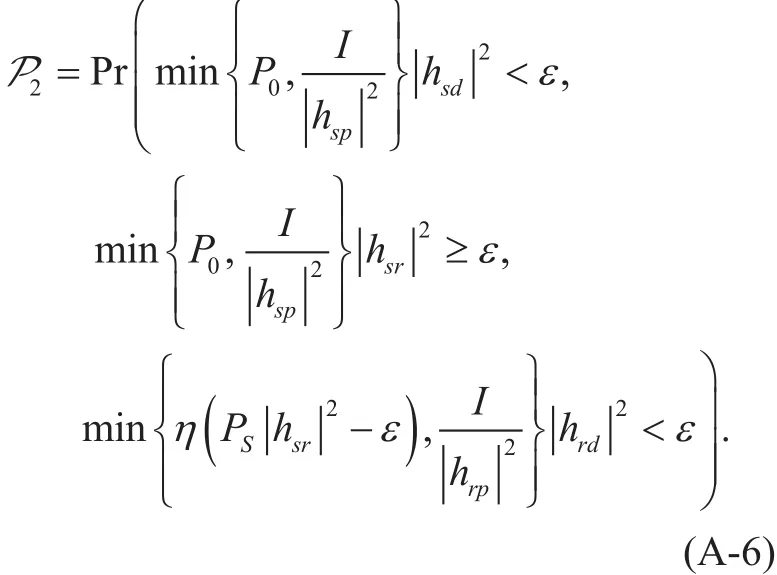
Note thatP2can be expressed as (A-7) at the top of page 38,

where

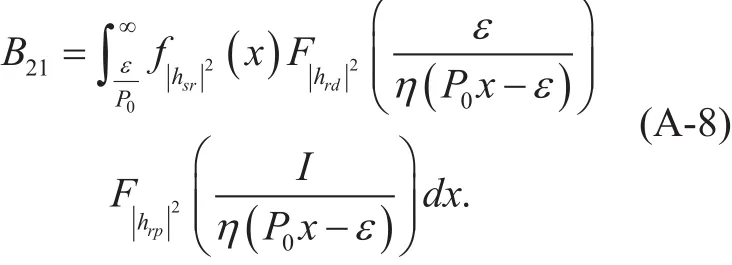
Employing [23, eq. (1.110)], [23, eq.(3.351.3)], [23, eq. (3.471.9)] and performing the change of variablesB21can be readily deduced. Similarly,B22can be expressed as

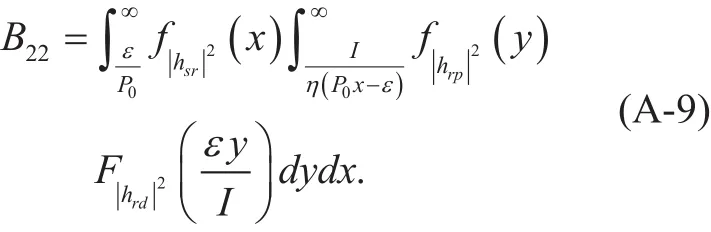
By performing the change of variablesand employing [23, eq. (3.351.1)],B23can be expressed as

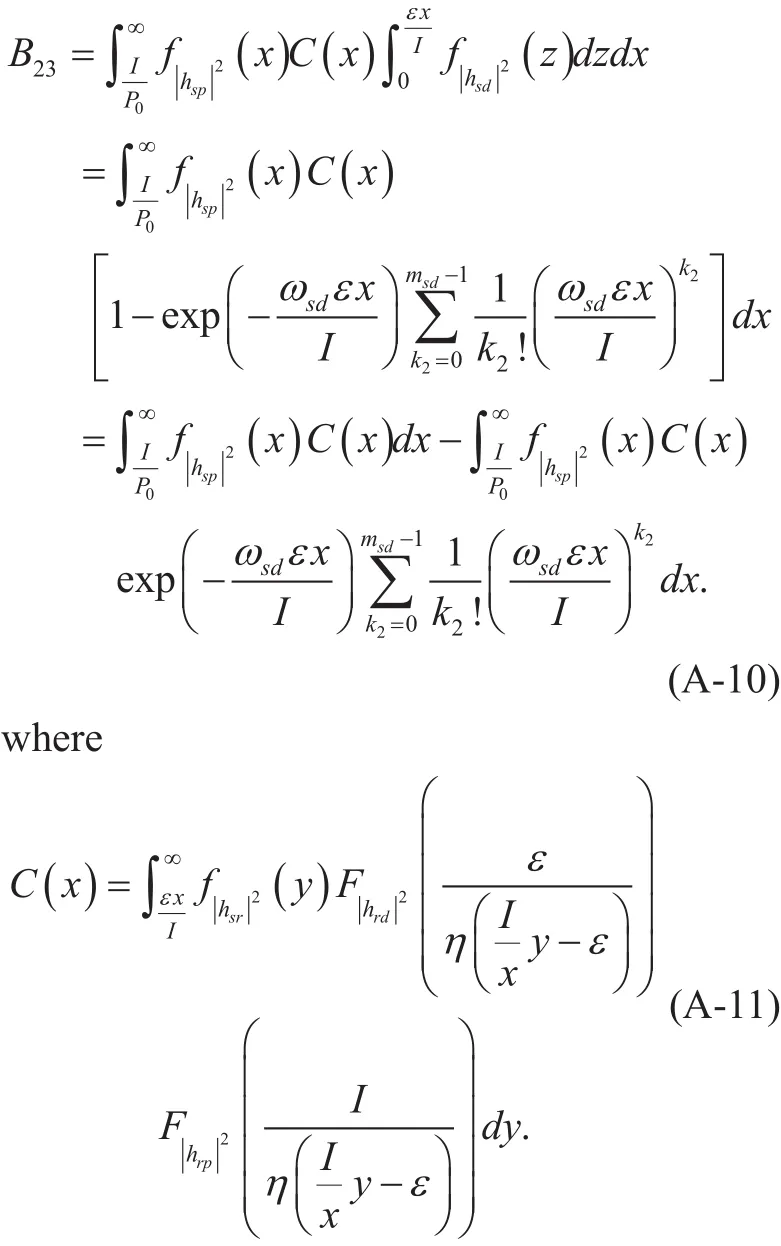
Finally, by employing [23, eq. (1.110)], [23,eq. (3.351.3)] and [23, eq. (3.471.9)],B23can be readily obtained.

The derivation ofB24is similar to that ofB23, i.e.,

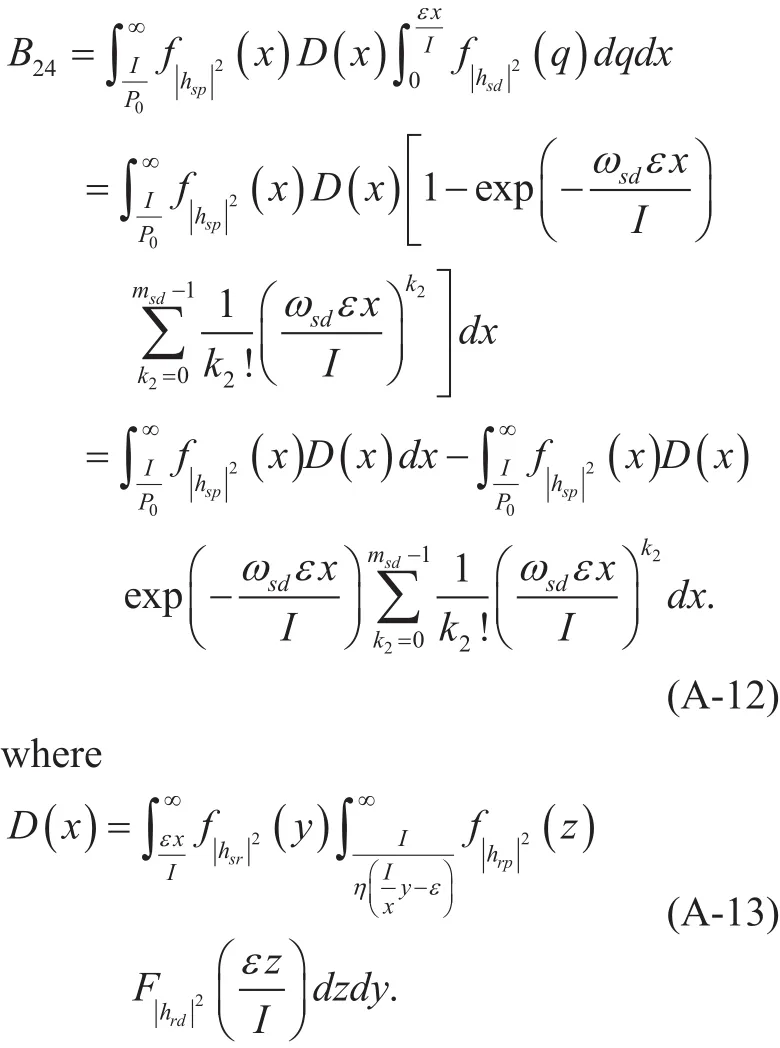
Substituting (A-8)-(A-12) into (A-7) and utilizing Lemma 1,P2is readily obtained,thus completing the proof.

ACKNOWLEDGEMENTS

This work of J. Yang was supported in part by the National Natural Science Foundation of China (Grant No. 61472343) and China Postdoctoral Science Foundation (Grant No.2014M56074).

References

[1] T. T. Duy and H. Y. Kong, “Performance analysis of mixed amplify-and-forward and decode-and-forward protocol in underlay cognitive networks,”China Communications, vol. 13,no. 3, 2016, pp. 115-126.

[2] X. Zhang, J. Xing, Z. Yan, Y. Gao, and W. Wang,“Outage performance study of cognitive relay networks with imperfect channel knowledge,”IEEE Communications Letters, vol. 17, no. 1,2013, pp. 27-30.

[3] P. Yang, L. Luo, and J. Qin, “Outage performance of cognitive relay networks with interference from primary user,”IEEE Communications Letters, vol. 16, no. 10, 2012, pp. 1695-1698.

[4] C. Zhong, T. Ratnarajah, and K. K. Wong, “Outage analysis of decode-and-forward cognitive dual-hop systems with the interference constraint in Nakagami-mfading channels,”IEEE Transactions on Vehicular Technology, vol. 60, no. 6,2011, pp. 2875-2879.

[5] J. Wang, Z.～Zhang, Q. Wu, and Y. Huang, “Outage analysis of cognitive relay networks with interference constraints in Nakagami-mchannels,”IEEE Wireless Communications Letters, vol.2, no. 4, 2013, pp. 387-390.

[6] X. Zhang, Y. Zhang, Z. Yan, J. Xing, and W.Wang, “Performance analysis of cognitive relay networks over Nakagami-mfading channels,”Selected Areas in Communications IEEE Journal on, vol. 33, no. 5, 2015, pp. 865-877.

[7] S. S. Ikki and M. H. Ahmed, “Performance analysis of decode-and-forward incremental relaying cooperative-diversity networks over Rayleigh fading channels,”Proc. Vehicular Technology Conference, 2009. Vtc Spring 2009.IEEE, 2009,pp. 1-6.

[8] K. Tourki, K. A. Qaraqe, and M. S. Alouini, “Outage analysis for underlay cognitive networks using incremental regenerative relaying,”IEEE Transactions on Vehicular Technology, vol. 62,no. 2, 2013, pp. 721-734.

[9] Y. Chang, Y. Li, Z. Si, and Y. Lu, “Outage analysis of cognitive incremental DF relay network in Nakagami-mfading channels,”Proc. Vehicular Technology Conference, 2015, pp. 1-5.

[10] H. Y. Huang, Z. Li, J. B. Si, and R. Gao, “Outage analysis of underlay cognitive multiple relays networks with a direct link,”IEEE Communications Letters, vol. 17, no. 8, 2013, pp. 1600-1603.

[11] B. Gurakan, O. Ozel, J. Yang, and S. Ulukus,“Energy cooperation in energy harvesting communications,”IEEE Transactions on Communications, vol. 61, no. 12, 2013, pp. 4884-4898.

[12] Z. Ding, C. Zhong, D. W. K. Ng, and M. Peng,“Application of smart antenna technologies in simultaneous wireless information and power transfer,”IEEE Communications Magazine, vol.53, no. 4, 2015, pp. 86-93.

[13] H. S. Nguyen, A. H. Bui, D. T. Do, and M. Voznak,“Imperfect channel state information of AF and DF energy harvesting cooperative networks,”China Communications, vol. 13, no. 10, 2016,pp. 11-19.

[14] Z. Wen, X. Liu, Y. Chen, R. Wang, and Z. Xie,“Joint transceiver designs for full-duplex MIMO SWIPT systems based on MSE criterion,”China Communications, vol. 13, no. 10, 2016, pp. 79-85.

[15] A. Dong, H. Zhang, M. Shu, and D. Yuan, “Simultaneous wireless information and power transfer for MIMO interference channel networks based on interference alignment,”Entropy, vol.19, no. 9, 2017, pp. 484-509.

[16] Y. Liu, S. A. Mousavifar, Y. Deng, C. Leung, and M. Elkashlan, “Wireless energy harvesting in a cognitive relay network,”IEEE Transactions on Wireless Communications, vol. 15, no. 4, 2016,pp. 2498-2508.

[17] K. Xiong, Y. Zhang, Y. Chen, and X. Di, “Power splitting based SWIPT in network-coded twoway networks with data rate fairness: an information-theoretic perspective,”China Communications, vol. 3, no. 12, 2017, pp. 107-119.

[18] Z. Wang, Z. Chen, B. Xia, L. Luo, and J. Zhou,“Cognitive relay networks with energy harvesting and information transfer: design, analysis,and optimization,”IEEE Transactions on Wireless Communications, vol. 15, no. 4, 2016, pp. 2562-2576.

[19] Z. Yang, Z. Ding, P. Fan, and G. K. Karagiannidis,“Outage performance of cognitive relay networks with wireless information and power transfer,”IEEE Transactions on Vehicular Technology, vol. 65, no. 5, 2016, pp. 3828-3833.

[20] Z. Deng, X. Liu, M. Jia, and W. Lu, “Sensing time optimization in energy-harvesting cognitive radio with interference rate control,”China Communications, vol. 13, no. 1, 2016, pp. 47-56.

[21] Y. Liu, “Wireless information and power transfer for multirelay-assisted cooperative communication,”IEEE Communications Letters, vol. 20, no.4, 2016, pp. 784-787.

[22] H. Li, C. Huang, F. Alsaadi, and S. Cui, “Performance analysis for energy harvesting communication systems: from throughput to energy diversity,”Proc. IEEE Global Communications Conference, 2015, pp. 1-6.

[23] I. S. Gradshteyn and I. M. Ryzhik,table of Integrals, Series, and Products, 7thed. New York:Academic Press, 2017.

[24] A. P. Prudnikov, Y. A. Brychkov, and O. I.Marichev, “Integrals and series. volume 3: More special functions.”Revista De Ciencias Farmaceuticas, 1989.

[25] R. P. Agarwal, “An extension of Meijer’s G-function,”Proc. Nat. Inst. Sci:india Part A, 1965, pp.536-546.

[26] I. S. Ansari, S. Al-Ahmadi, F. Yilmaz, M. S. Alouini, and H. Yanikomeroglu, “A new formula for the BER of binary modulations with dual-branch selection over generalized-K composite fading channels,”IEEE Transactions on Communications, vol. 59, no. 10, 2012, pp. 2654-2658.

[27] K. P. Peppas, “A new formula for the average bit error probability of dual-hop amplify-and-forward relaying systems over generalized shadowed fading channels,”IEEE Wireless Communications Letters, vol. 1, no. 2, 2012, pp. 85-88.