Xingjian Lin·Guoyi He·Xinyi He·Qi Wang·Longsheng Chen

1 Introduction

The schooling of fish is a common phenomenon in nature.The most cited function of such schooling behavior is to gain an extra hydrodynamic advantage while swimming[1].The fluid-structure interactions between the swimming bodies and the surrounding flow are the key to understanding the schooling behavior of fish[2,3],because each individual is swimming in a complex flow pattern that is altered by the other members[4,5].Laboratory observations have revealed that a live trout shows slalom movement between vortex cores with decreased muscle activity[6],and that even a dead fish can undulate upwards in the vortex flow generated by a cylinder[7].Moreover,a live fish always obliquely swims behind a propelling robot fish[8].Thus,both the active and passive responses of the bodies following the surrounding flow are beneficial for achieving swimming performance[9].

With the development of advanced numerical techniques,the complex hydrodynamic reactions in a school of fish can be numerically investigated.The passive fluid-structure interactions between the fish and the surrounding flow are also investigated using the flexible filaments immersed in the uniform incoming flow[10].The in-phase and antiphase oscillations of two paratactic filaments with different separation distances have been studied[11].The inverted drafting phenomenon of two tandem filaments has also been investigated[12],in which the downstream filament has a larger drag than the upstream body[13].Furthermore,destructive interactions between two tandem filaments have been observed at certain spacings and Reynolds numbers,in which the follower experiences less drag and a smaller amplitude than the leader[14].Moreover,the fluid-structure interactions of multiple flexible filaments have been studied.The flapping motions and drag variations of individuals are deeply affected by their spacing[15].Wiggling hydrofoils in tandem or side-by-side arrangements have also been used to investigate the active fluid-structure interactions in schools of fish.In the tandem formation,the front fish can achieve an increased thrust,whereas that of the rear fish is decreased[16].In the side-by-side formation,in-phase fish schools have an advantage on power consumption compared to anti-phase fish schools[17].The oblique formation is the ubiquitous arrangement in a school of fish and is a combination of tandem and paratactic arrangements.A study investigating the hydrodynamic interactions between two oblique hydrofoils is worthwhile because it enables not only a full understanding of the intrinsic mechanism in a school of fish but also the optimization of coordinated motions of bio-robots[18].

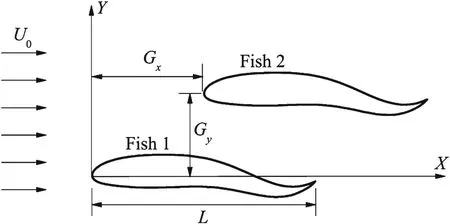
Fig.1 Physical model of an oblique school of fish

In this study,we represent a school of fish as two wiggling hydrofoils in an oblique arrangement and simulate the 2-D incompressible flow over the school of fish using an immersed boundary technique[19].We show that the propulsive characteristics of the individuals and entire school are deeply affected by their spacing.The remainder of the paper is arranged as follows.We describe the physical problem and numerical method in Sect.2.The third section contains two subsections.We discuss the propulsive performance of the in-phase school of fish in Sect.3.1 and that of the anti-phase school of fish in Sect.3.2.Finally,a few conclusions are summarized in the final section.

2 Physical problem and numerical method

The school of fish is simplified as two undulated hydrofoils in an oblique formation,as shown in Fig.1.The surrounding 2-D fluid is considered as incompressible with viscous uniform oncoming flow,as governed by the N–S equations

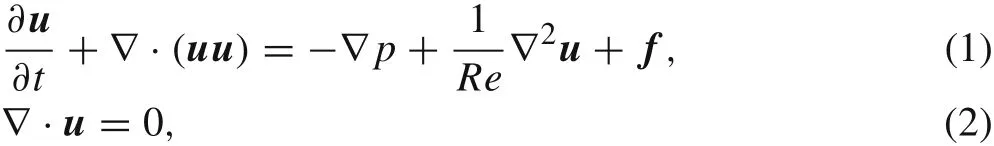
whereuandprepresent the flow velocity and pressure,respectively,andfdenotes the Eulerian force density that describes the fluid-structure interactions between the fish and the surrounding flow.An immersed boundary technique[19]is used to calculate the interaction force.The full procedures and validations of the immersed boundary technique are available elsewhere[20,21].

The undulation motion along the fish body is prescribed as

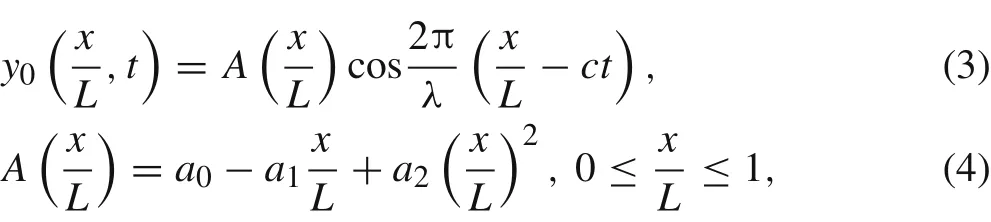
wherey0is the vertical displacement of the middle-line along the fish body,A(x/L)represents the undulated amplitude along the fish body,Lshows the length of the fish body,λandcdenote the wavelength and the phases peed respectively,and coefficientsa0=0.02,a1=0.0825,anda2=0.1625 are calculated from Ref.[17].The dimension less separations are achieved by dividing the length of the fish body as horizontal separation distanceDx=Gx/Land lateral separation distanceDy=Gy/L.

To analyze the propulsive performance of the individuals in the oblique school of fish,we calculate the mean values of the thrust coefficient and the power coefficient for each fish as follows[22]

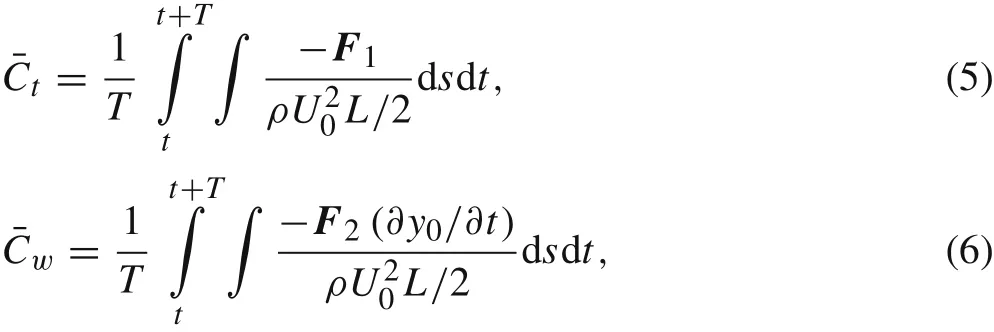
whereF1andF2represent the horizontal and vertical components of the interaction force acting on the fish body,respectively.Thus,the propulsive efficiency can be calculated as follows[22]

3 Results and discussion

The values of the control parameters used in our current simulations are set as follows:Re=200.0,U0=1.0,L=1.0,λ=1.0,c=5.0,0.0≤Dx≤3.0,and 0.3≤Dy≤0.6.

The effect of the separation distance along the swimming direction on the propulsive performance is analyzed in this paper.

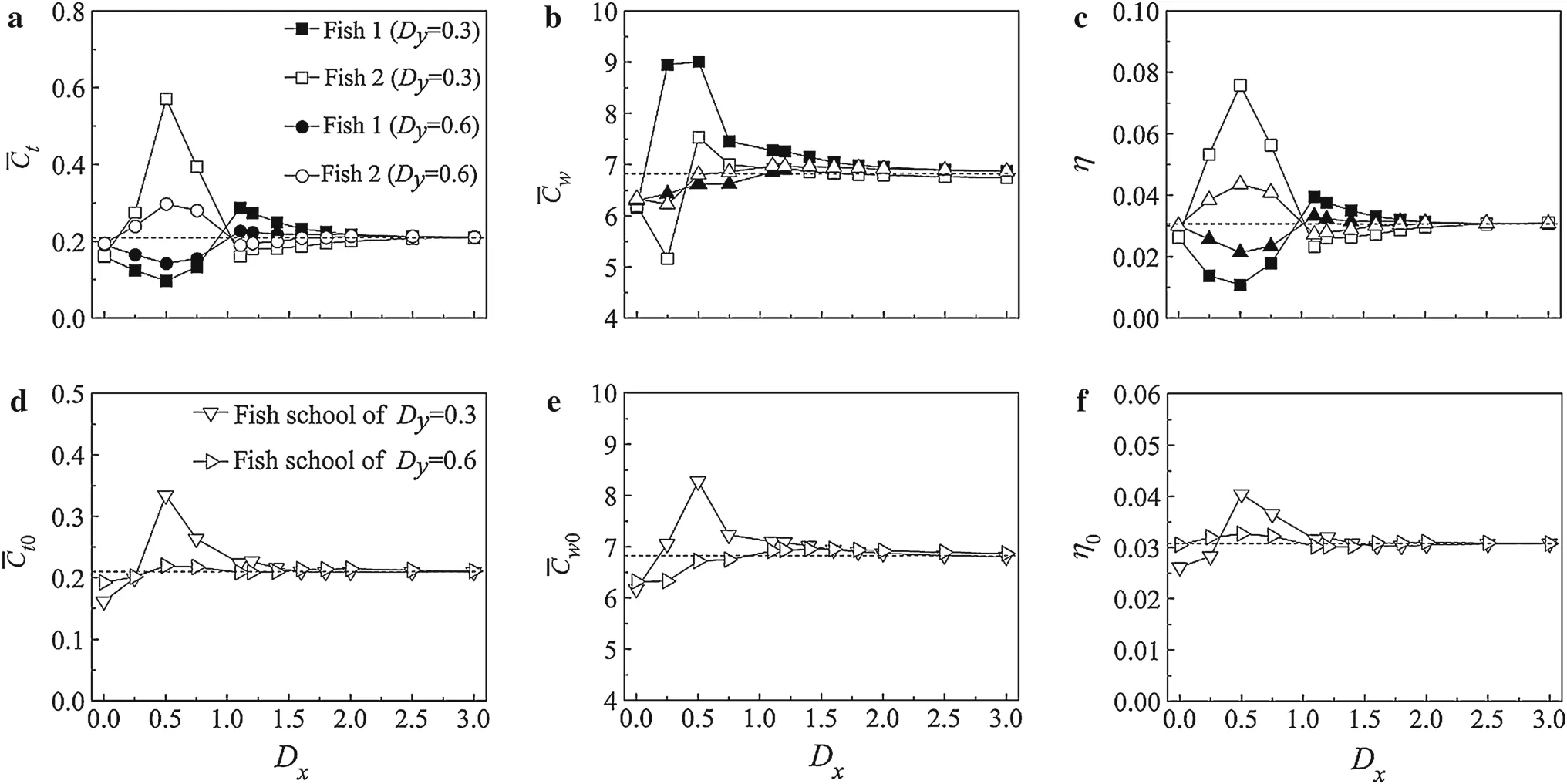
Fig.2 The mean values of the thrust coefficient(plots a,d),power coefficient(plots b,e),and propulsive efficiency(plots c,f)for each fish(the upper row)and the entire in-phase school(the lower row).The dashed lines represent the corresponding values of the variants of the isolated fish

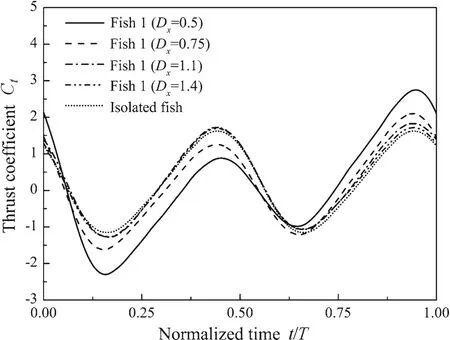
Fig.3 Time dependent thrust coefficient of fish 1 during one cycle with 0.5≤Dx≤1.4(Dy=0.3)

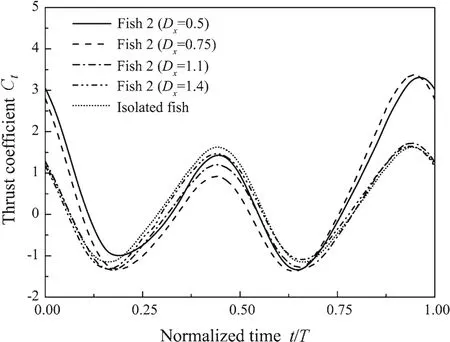
Fig.4 Time dependent thrust coefficient of fish 2 during one cycle with 0.5≤Dx≤1.4(Dy=0.3)

3.1 In-phase swimming fish

Figure 2 shows the propulsive performance for the two in phase swimming fish with different spacing values.The filled and empty symbols represent the upstream fish and downstream fish,respectively.WhenDx＜1.0,the upstream fish has a smaller time-averaged thrust coefficient and lower propulsive efficiency than the isolated fish.However,the downstream fish has a larger mean thrust coefficient and greater propulsive efficiency than the isolated fish.Moreover,when two fish swim in a paratactic formation(Dx=0.0),the mean thrust coefficient and power coefficient for each individual are smaller than those of the isolated individual.Therefore,the propulsive efficiency,it conforms to the previous result[17].WhenDx＞1.0,the leader generates increased thrust and efficiency,but the follower produces reduced thrust and efficiency,compared to those of the isolated fish.WhenDx=2.0,both individuals perform similar to the isolated fish.For the entire in-phase propelling school,worse propulsive performance is obtained withDx=0.0 and 0.25,comparing to the cases withDx=0.5 and 0.75.The best propulsive performance with the largest thrust force and the highest propulsive efficiency is observed for the oblique school of fish withDx=0.5,although more power is required.It may notice that all the propulsive efficiency reported in our current study are＜10%,it may due to the definition of Eq.(7)in which only the thrust coefficient is considered.

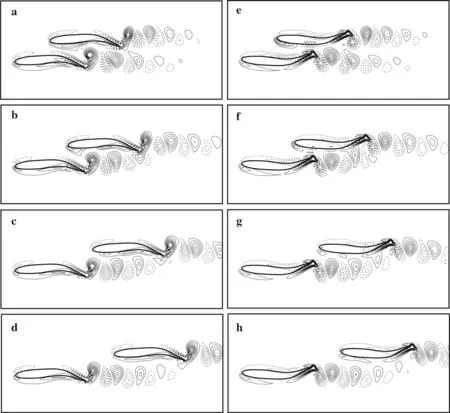
Fig.5 Vorticity contours of an in-phase school of fish at a–d t/T=0.5 and e–h t/T=1.0.The oblique spacings are a,d Dx=0.5,Dy=0.3,b,f Dx=0.75,Dy=0.3,c,g Dx=1.1,Dy=0.3,and d,h Dx=1.4,Dy=0.3.The solid and dashed lines denote positive and negative values,respectively

Figures 3 and 4 show the thrust variations of fish 1 and fish 2,respectively,for one cycle with 0.5≤Dx≤1.4.Figure 5 shows the vortex structure in the wake of an oblique school of fish with different longitudinal spacing values.WhenDx＜1.0,the leader has an obvious decreased thrust at 0.5Tbecause its vortex transportation is hindered by the follower,as shown in Fig.5a,b;and the follower has an increased thrust at 1.0Tbecause of the additional push force generated by the deflected vortices shed from the leader,as shown in Fig.5e,f.Thus,the leader performs worse,while the follower performs better,than a single fish whenDx＜1.0.WhenDx＞1.0,the thrust of the leader is increased at 1.0Tbecause of the obstruction mechanism[23]produced by the follower,as shown in Fig.5g,h;moreover,the thrust for the follower is decreased at 0.5Tbecause it experiences the jet flow generated by its front partner,as shown in Fig.5c,d.Therefore,the leader performs better,while the follower performs worse,than a single fish whenDx＞1.0.

3.2 Anti-phase swimming fish

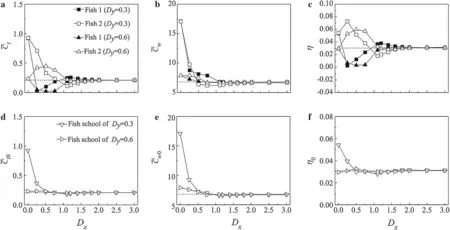
Fig.6 The mean values of the thrust coefficient(plots a,d),power coefficient(plots b,e),and propulsive efficiency(plots c,f)for each fish(the upper row)and the entire anti-phase school(the lower row).The dashed lines represent the corresponding values of the variants of the isolated fish

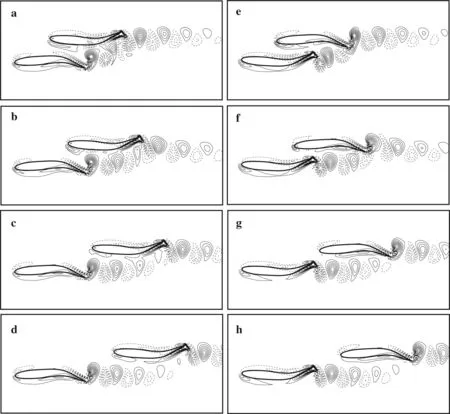
Fig.7 Vorticity contours of an anti-phase school of fish at a–d t/T=0.5 and e–h t/T=1.0.The oblique spacings are a,d Dx=0.5,Dy=0.3,b,f Dx=0.75,Dy=0.3,c,g Dx=1.1,Dy=0.3,and d,h Dx=1.4,Dy=0.3.The solid and dashed lines denote positive and negative values,respectively

Figure6 shows the propulsive performance of two anti-phaseswimming fish at different separation distances.WhenDx＜1.0,the rear fish has a larger mean thrust coefficient and a higher time-averaged propulsive efficiency,but the front fish has a smaller thrust coefficient and a lower propulsive efficiency compared to those of a single fish.On one hand,the rear fish feels the additional pull force generated by the vortices shed from the front fish at 0.5T,as shown in Fig.7a,b;on the other hand,the vortex transportation of the front fish is hindered by the rear fish at 1.0T,as shown in Fig.7e,f.Moreover,the individuals in the paratactic school(Dx=0.0)have a larger thrust coefficient and larger power coefficient than the isolated fish,that exhibit behavior that is consistent with previously reported results[17].WhenDx＞1.0,the front fish exhibits a better propulsive performance than the rear fish because the downstream body experiences the jet flow in the wake of the upstream body,as shown in Fig.7c,d,g,h.WhenDx＞2.0,both individuals swim like a single fish.For the entire anti-phase wiggling school of fish,both the thrust coefficient and propulsive efficiency increase whenDx=0.0 and 0.25,compared to the isolated fish,although greater power is consumed.Moreover,the oblique school of fish has the best performance whenDx=0.0,due to the mirror image ground effect[24];but when the longitudinal spacing exceedsDx=0.5,such ground effect disappears,thus,the school of fish performs similar to an isolated fish.

4 Conclusions

To investigate the fluid-structure interactions in a school of fish,the two-dimensional incompressible flow over two oblique hydrofoils was simulated using an immersed boundary technique.The separation distance between the individuals significantly affected the fluid-structure interactions.WhenDx＜1.0,the rear fish exhibited an increased propulsive force and efficiency,whereas the front fish exhibited a decreased propulsive thrust and efficiency compared to those of an isolated fish.WhenDx＞1.0,the thrust and efficiency of the anterior fish increased compared to those of a single fish;however,the corresponding values for the posterior fish decreased.For the entire oblique school of fish,the anti-phase school exhibited the largest propulsive thrust and efficiency when swimming in a side-by-side formation.

AcknowledgementsThe work was supported by the National Natural Science Foundation of China(Grant 11462015).

1.Weihs,D.:Hydromechanics of fish schooling.Nature 241,290–291(1973)

2.Krebs,J.:Fish schooling.Nature 264,701–701(1976)

3.Liu,H.,Kolomenskiy,D.,Nakata,T.,et al.:Unsteady bio- fluid dynamics in flying and swimming.Acta Mech.Sin.33,663–684(2017)

4.Liao,J.C.:A review of fish swimming mechanics and behaviour in altered flows.Philos.Trans.R.Soc.Lond.B Biol.Sci.362,1973–1993(2007)

5.Wang,S.Z.,He,G.W.,Zhang,X.:Self-propulsion of flapping bodies in viscous fluids:recent advances and perspectives.Acta Mech.Sin.32,980–990(2016)

6.Liao,J.C.,Beal,D.N.,Lauder,G.V.,et al.:Fish exploiting vortices decrease muscle activity.Science 302,1566–1569(2003)

7.Beal,D.N.,Hover,F.S.,Triantafyllou,M.S.,et al.:Passive propulsion in vortex wakes.J.Fluid Mech.549,385–402(2006)

8.Marras,S.,Porfiri,M.:Fish and robots swimming together:attraction towards the robot demands biomimetic locomotion.J.R.Soc.Interface 9,1856–1868(2012)

9.Fish,F.E.,Lauder,G.V.:Passive and active flow control by swimming fishes and mammals.Annu.Rev.Fluid Mech.38,193–224(2006)

10.Shelley,M.J.,Zhang,J.:Flapping and bending bodies interacting with fluid flows.Annu.Rev.Fluid Mech.43,449–465(2011)

11.Favier,J.,Revell,A.,Pinelli,A.:Numerical study of flapping filaments in a uniform fluid flow.J.Fluids Struct.53,26–35(2015)

12.Zhu,L.D.:Interaction of two tandem deformable bodies in a viscous incompressible flow.J.Fluid Mech.635,455–475(2009)

13.Ristroph,L.,Zhang,J.:Anomalous hydrodynamic drafting of interacting flapping flags.Phys.Rev.Lett.101,194502(2008)

14.Kim,S.,Huang,W.X.,Sung,H.J.:Constructive and destructive interaction modes between two tandem flexible flags in viscous flow.J.Fluid Mech.661,511–521(2010)

15.Uddin,E.,Huang,W.X.,Sung,H.J.:Interaction modes of multiple flexible flags in a uniform flow.J.Fluid Mech.729,563–583(2013)

16.Khalid,M.S.U.,Akhtar,I.,Dong,H.B.:Hydrodynamics of a tandem fish school with asynchronous undulation of individuals.J.Fluids Struct.66,19–35(2016)

17.Dong,G.J.,Lu,X.Y.:Characteristics of flow over traveling wavy foils in a side-by-side arrangement.Phys.Fluids19,057107(2007)

18.Hemelrijk,C.K.,Reid,D.A.P.,Hildenbrandt,H.,et al.:The increased efficiency of fish swimming in a school.Fish Fish.16,511–521(2015)

19.Su,S.-W.,Lai,M.-C.,Lin,C.-A.:An immersed boundary technique for simulating complex flows with rigid boundary.Compt.Fluids 36,313–324(2007)

20.He,G.Y.,Zhang,S.G.,Zhang,X.:Thrust generation and wake structure of wiggling hydrofoil.J.Appl.Math.Mech.31,585–592(2010)

21.He,G.Y.,Wang,Q.,Zhang,X.,et al.:Numerical analysis on transitions and symmetry-breaking in the wake of a flapping foil.Acta Mech.Sin.28,1551–1556(2012)

22.Uchiyama,T.,Kikuyama,K.:Numerical study on the propulsive performance of a submerged wiggling micromachine in straight conduit.J.Micromech.Microeng.14,409–418(2005)

23.Tian,F.B.,Luo,H.X.,Zhu,L.D.,et al.:Interaction between a flexible filament and adownstream rigid body.Phys.Rev.E 82,026301(2010)

24.Fang,F.,Ho,K.L.,Ristroph,L.,et al.:A computational model of the flight dynamics and aerodynamics of a jelly fish-like flying machine.J.Fluid Mech.819,621–655(2017)