Takasar Hussain·Faiz Ahmad·Muhammad Ozair

1 Introduction

Elastic waveguides in the form of a cylinder are commonly used in industry as pipes for gases or liquids.Guided waves have great applications in nondestructive testing of materials[1,2].Nondestructive testing(NDT)of materials is a branch of mechanical engineering,in which materials are tested without any damage,such as to detect cracks and fatigue[3,4].Lamb modes can be used to detect defects in pipelines[5].A study by Ces et al.[6]has shown that elastic constants of the materials can be measured by using the zero group velocity(ZGV)modes.For a transversely isotropic Zircaloy tube,they extracted four out of five constants directly from the ZGV resonance frequencies.ZGV modes have also been used to estimate the thickness of an adhesive layer[7].Characteristics of group velocity of backward waves have been discussed in a hollow cylinder[8].The work of Tolstoy and Usdin[9]predicted the anomalous behavior ofS1Lamb mode for an isotropic plate with Poisson ratio.TheS1mode has a ZGV point for almost all isotropic materials.For a material with,each of the modesSis found to be anomalous.Theoretical explanations for this peculiar behavior in an isotropic plate have been presented in Refs.[10,11].Recently,Yehand Yang[12]extracted the mechanical properties of an isotropic Zircaloy tube from the dispersion spectra of guided waves.Then,Ahmad[13]explained analytically why the shape of modes for an isotropic plate and a cylinder are similar in thek?cplane.The work of Hussain and Ahmad[14]considered ZGV points in the spectrum of Lamb modes in a compressible orthotropic plate.It was found that in addition to modes with a single ZGV point,a large number of modes exist with multiple such points.ZGV Lamb modes are discussed in an incompressible orthotropic plate by Hussain and Ahmad[15].In this paper,we shall discuss that ZGV modes also exist in an isotropic cylindrical waveguide as in the spectrum of plate.Pochhammer frequency equation[16]will be examined analytically by finding the slope of each mode at two different points in theω?cplane.

2 ZGV modes

We consider a cylinder of in finite length with diameterd=2h.The cylinder is of isotropic material,and its axis coincides with thezaxis.The frequency equation for the longitudinal modes,known as Pochhammer frequency equation,is given

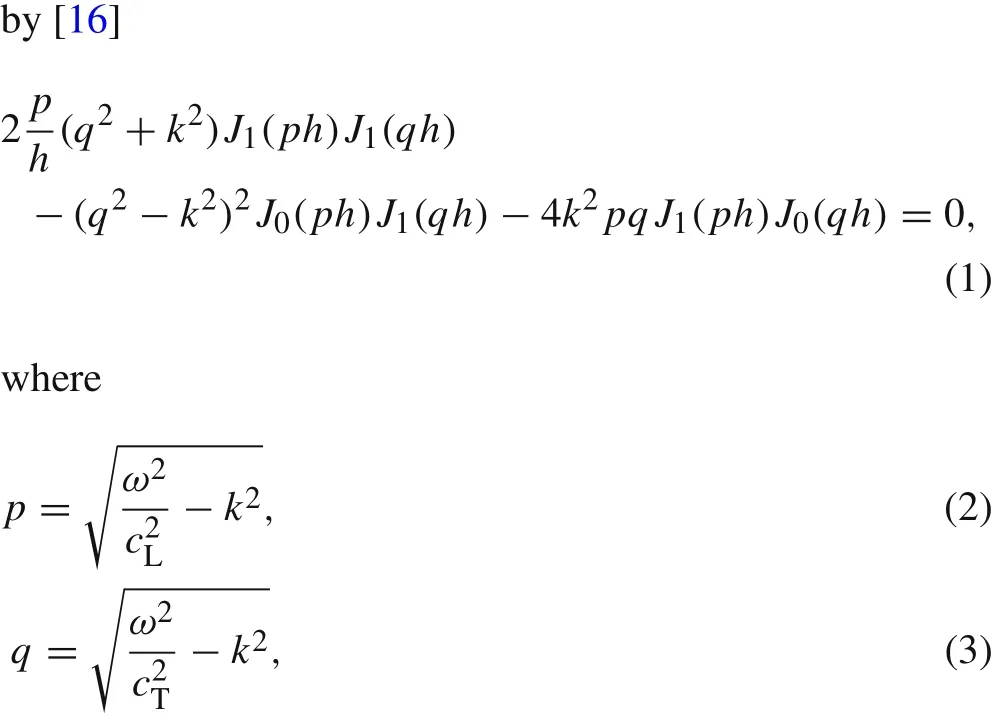
andJ0andJ1denote Bessel functions of the first kind.Also,cTandcL,respectively,denote the phase speeds of the transverse and longitudinal bulk waves in the material andωandk,respectively,denote the frequency and the wave number of the mode.The phase velocity,c,of a mode is given by

We will calculate the derivativeat two positions of the spectrum.We write

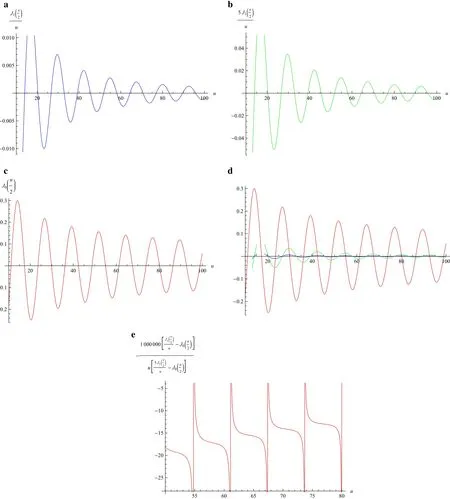
Fig.1 a Plot of function.b Plot of function.c Plot of function.d Comparison of a,b,and c.e Plot of Eq.(16)

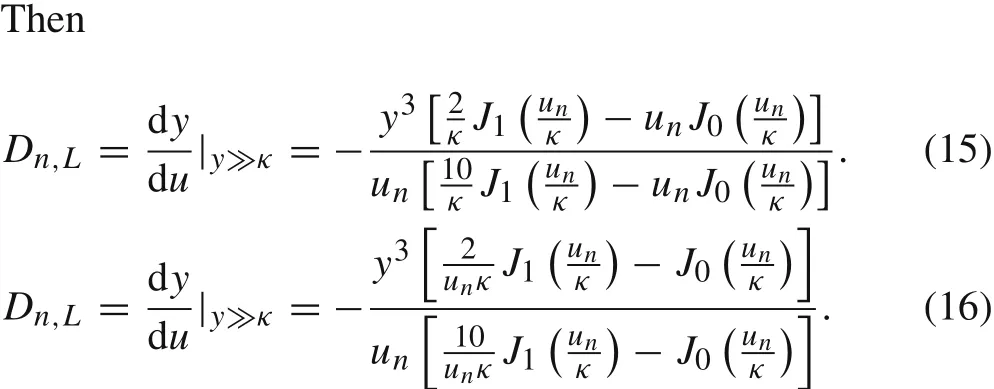
We shall investigate the sign of Eq.(16)for higher modes as follows.We know that for higher modesuis large and also it lies in the denominator of both functionsanddominates these functions.It can be seen in Fig.1 withκ=2(one can choose any value ofκ).

From Fig.1d,we can easily see thatdominates other two functions for largeu,hence sign of the Eq.(16)

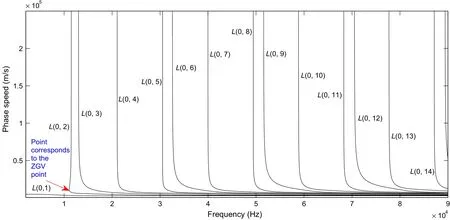
Fig.2 The spectrum of nickel isotropic cylinder with c L=6000 m/s,c T=3000 m/s,and κ=2,no mode has ZGV point except L(0,2)and L(0,5)

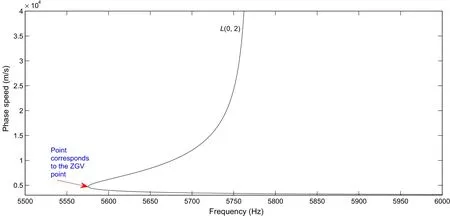
Fig.3 The L(0,2)mode for a material with c L=3000 m/s,c T=2000 m/s,and κ=1.5

will remain negative,which is plotted in Fig.1e.Thus,we conclude from Eqs.(11)and(16)that no higher mode will be anomalous for all isotropic materials.

We can also give the argument for the sign of Eq.(16)to be negative whenuis large,as follows.

As we know,the behavior of Bessel functions is oscillatory,so they have in finitely many zeroes,and hence their sign can be positive or negative.We have the following cases for Bessel functions.

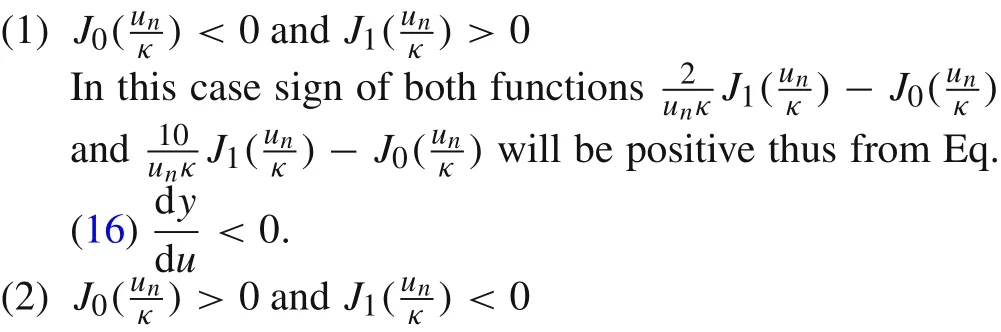
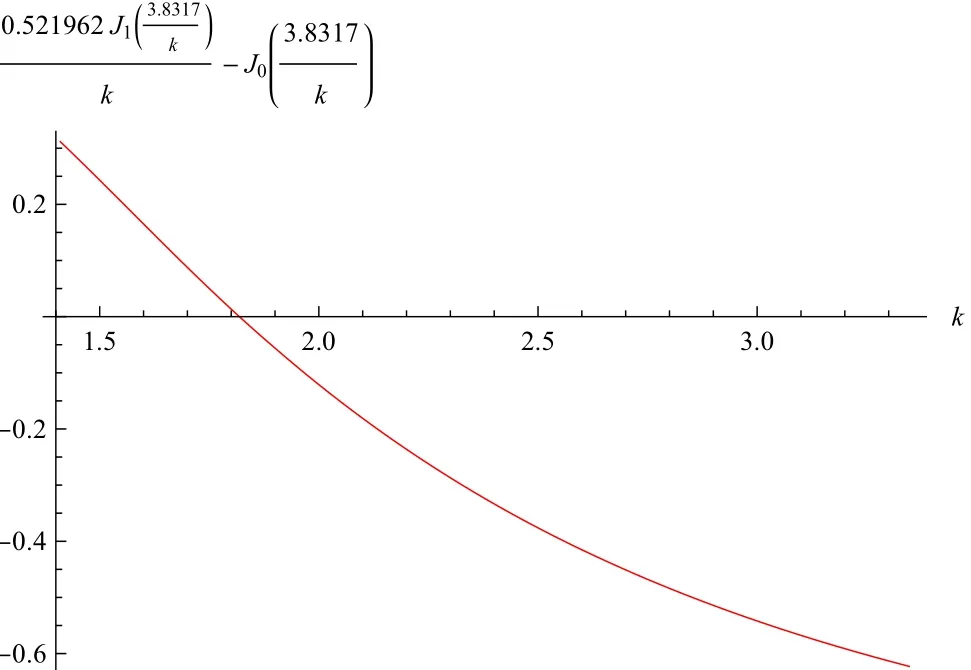
Fig.4 Plot ofwhen u=3.8317

In all these cases we have seen that the sign of Eq.(16)remains negative.Thus,we conclude from Eqs.(11)and(16)that no higher mode will be anomalous for all isotropic materials.

As shown in Fig.2,which is plotted for nickel withκ=2.

To check the first mode we shall argue as follows.From Eq.(12),for a large positivey,the sign of the right hand side must be positive and the denominator should be small.

Whenthe first mode,L(0,2),occurs for a large phase velocity,by taking

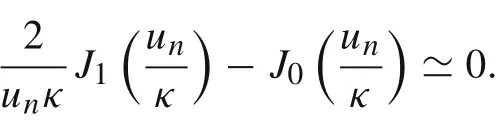
For example,whenκ=1.5, first non-zero root of above equation is 2.88496.Figure 3 exhibitsL(0,2)mode for this material.

Forκ＞1.82,the first mode exists for a large phase velocity due to

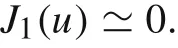
Its first non-zero root approximately gives the value of frequency for the first mode,L(0,2),say it isu1?3.8317.

As,0 andJ0(u1)is negative because the first two zeros ofJ0are 2.4048 and 5.5201,so for the sign of Eq.(12)to be positive,we have

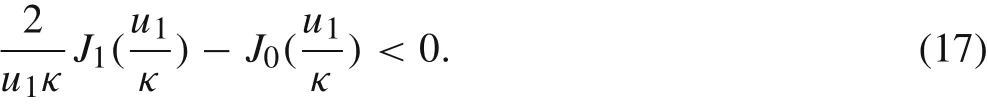
From the Fig.4we can see that Eq.(17)holds for1.82＜κ.Thus,the slope of the first mode from Eq.(16)is positive when＞0,it holds forHence,the first mode will be anomalous for materials havingFigure 5 shows the anomalous behavior ofL(0,2)mode for aluminium withκ=2.0820.

But,whenκ＞2.64,we havewhich ensures the normal behavior of first mode,because in this case Eq.(16)gives a negative slope for large phase velocityy.This is shown in Fig.6 for a material withκ=2.7.

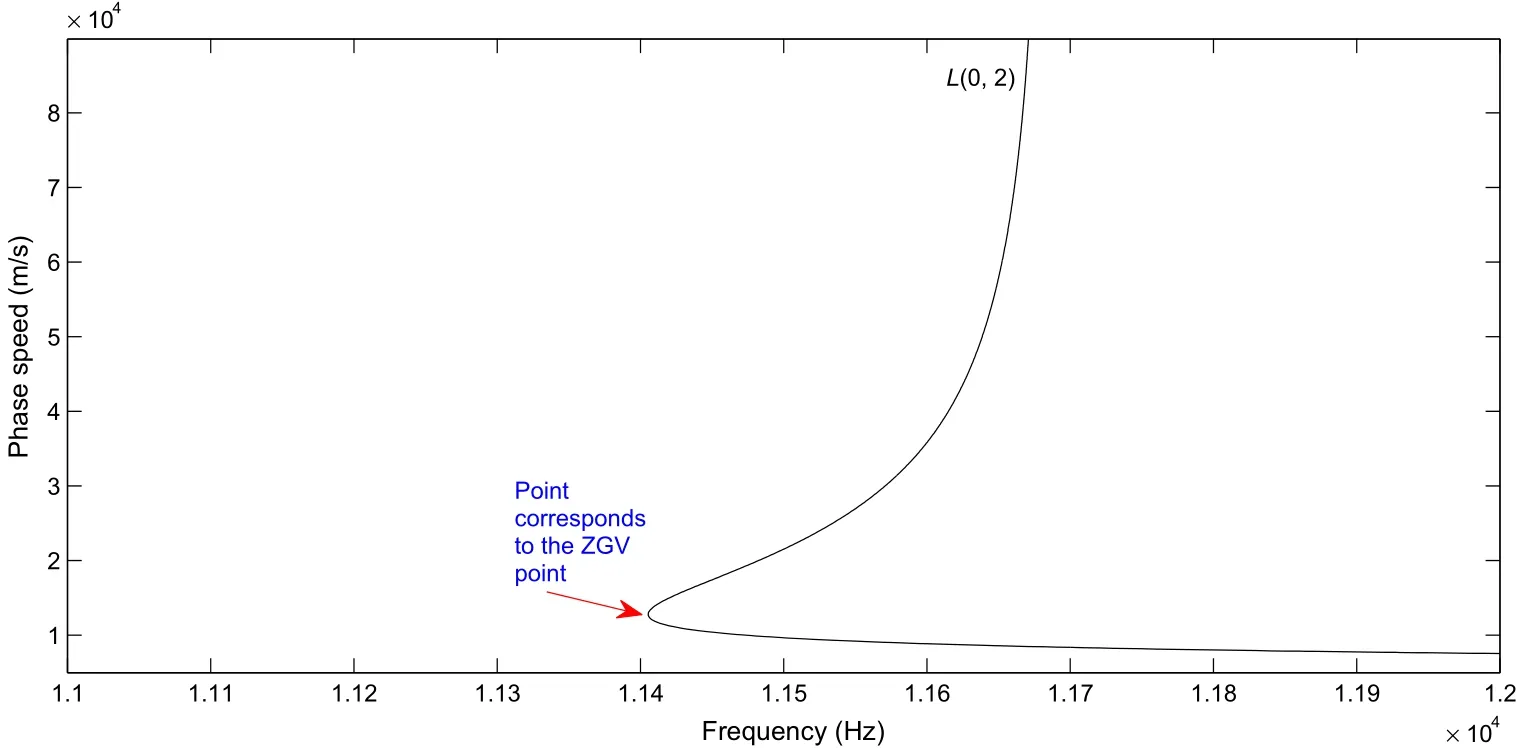
Fig.5 The longitudinal mode L(0,2)has a ZGV point for aluminium isotropic cylinder with c L=6350 m/s,c T=3050 m/s,and κ=2.0820

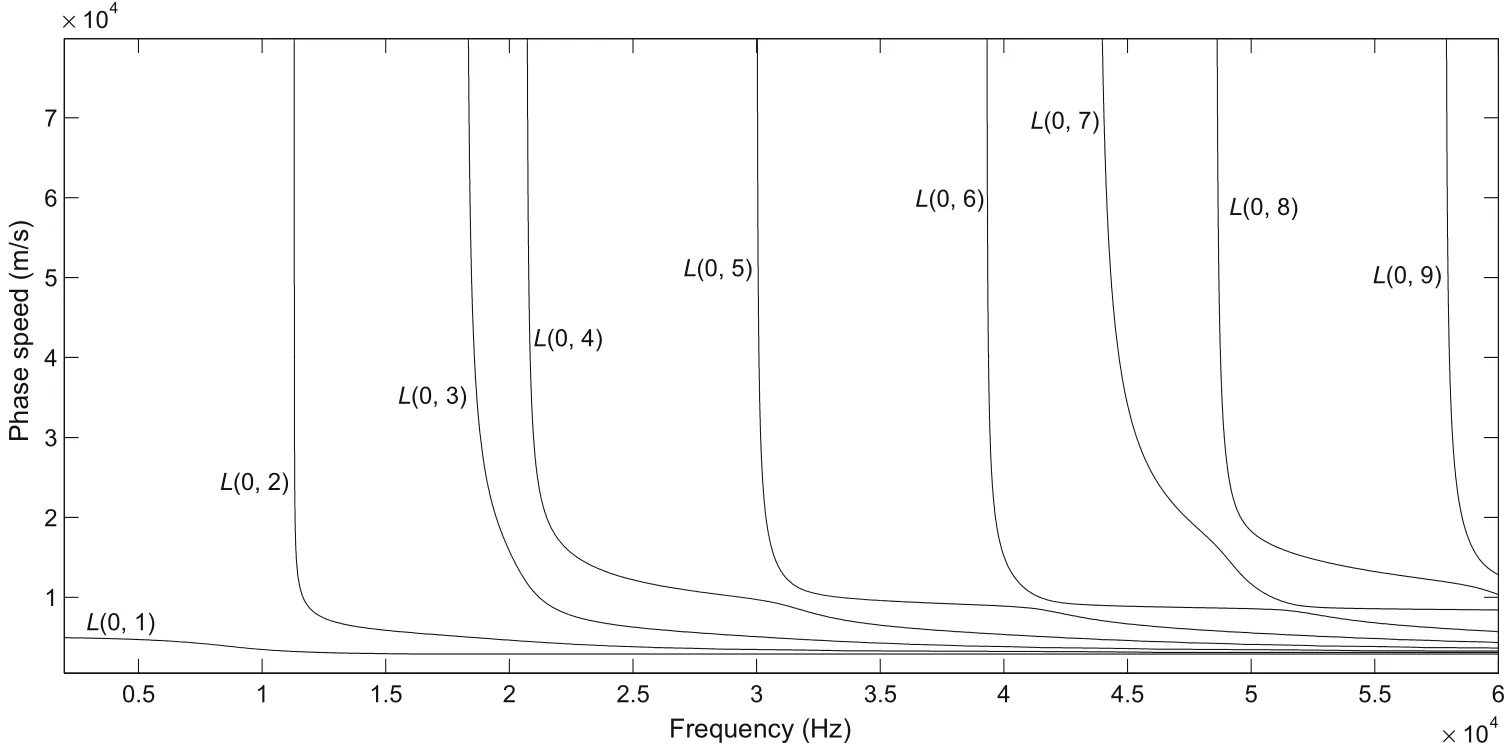
Fig.6 The longitudinal mode L(0,2)has no ZGV point for an isotropic material with c L=8000 m/s,c T=2950 m/s,and κ=2.7119

Fig.7 The longitudinal mode L(0,5)for an isotropic nickel cylinder with κ=2

3 Conclusion

We have examined the Pochhammer frequency equation by finding the slope of modes.It has been concluded that the first mode has a ZGV point for materials withmaterials withκ＞2.64,the first mode behaves normally.No higher mode,except the first few,with ZGV point exists in the spectrum of an isotropic cylinder.By comparison with plate,we have concluded that

(1)For a plate theS1mode is anomalous for3.347[17],but for the cylinderL(0,2)is anomalous whenand beyondκ=2.64 it loses its anomaly.

(2)Whenκ=2,the modesS3n+1,n=0,1,...are anomalous for the plate,but no higher mode is anomalous for the case of a cylinder.For example,in the case of nickel withκ=2,L(0,2)andL(0,5)are anomalous andL(0,i),i＞5are all normal.Figure2shows the behavior of the first 14 modes in which onlyL(0,2)andL(0,5)are anomalous,L(0,5)is shown separately in Fig.7.

AcknowledgementsThe authors are grateful to a referee for helpful comments which led to improvement of the paper.Takasar Hussain and Muhammad Ozair acknowledge financial support from the Higher Education Commission of Pakistan under Startup Research Grant Program(Grant 21-962/SRGP/R&D/HEC/2016).

1.Alleyne,D.N.:The nondestructive testing of plates using ultasonic lamb waves.[Ph.D.Thesis],University of London,UK(1991)

2.Staszewski,W.J.,Lee,B.C.,Traynor,R.:Fatigue detection in metallic structures with Lamb waves and 3D laser vibrometry.Meas.Sci.Technol.18,727–739(2007)

3.Chen,W.-Q.:Some recent advaces in 3D crack and contact analysisof elastic solids with tranverse isotropy and multifed coupling.Acta Mech.Sin.31,601–626(2015)

4.Song,Y.,Hu,H.,Rudnicki,J.R.:Normal compression wave scattering by a permeable crack in a fluid-saturated poroelastic solid.Acta Mech.Sin.33,356–367(2017)

5.Lowe,M.J.S.,Alleyne,D.N.,Caw ley,P.:Defect detection in pipes using guided waves.Ultrasonics 36,147–154(1998)

6.Ces,M.,Royer,D.,Prada,C.:Characterization of mechanical properties of hollow cylinder with zero group velocity Lamb modes.J.Acoust.Soc.Am.132,180–185(2012)

7.Cho,H.,Hara,Y.,Matsuo,T.:Evaluation of the thickness and bond quality of three-layered media using zero-group-velocity Lamb waves.J.Phys.Conf.Ser.520,012–023(2014)

8.Cui,H.,Lin,W.,Zhang,H.,et al.:Characteristics of group velocities of backward waves in a hollow cylinder.J.Acoust.Soc.Am.135,3398–3408(2014)

9.Tolstoy,I.,Usdin,E.:Wave propagation in elastic plates:Low and high mode dispersion.J.Acoust.Soc.Am.29,37–42(1957)

10.Werby,M.F.,Uberall,H.:The analysis and interpretation of some special properties of higher order symmetric Lambwaves:the case for plates.J.Acoust.Soc.Am.111,2686–2691(2002)

11.Kausel,E.:Number and location of zero group velocity modes.J.Acoust.Soc.Am.131,3601–3610(2012)

12.Yeh,C.-H.,Yang,C.-H.:Characterization of mechanical and geometrical properties of a tube with axial and circumferential guided waves.Ultrasonics 51,472–479(2011)

13.Ahmad,F.:A simple formula for the longitudinal modes in a cylinder.J.Acoust.Soc.Am.115,475–477(2003)

14.Hussain,T.,Ahmad,F.:Lamb modes with multiple zero-group velocity points in an orthotropic plate.J.Acoust.Soc.Am.132,641–645(2012)

15.Hussain,T.,Ahmad,F.:Existence of zero-group velocity modes in an incompressible plate.Arch.Mech.66,55–65(2014)

16.Achenbach,J.D.:Wave Propagation in Elastic Solids,Chap.6.North-Holland,Amsterdam(1980)

17.Prada,C.,Clorennec,D.,Royer,D.:Local vibration of an elastic plate and zero-group velocity Lamb modes.J.Acoust.Soc.Am.124,203–212(2008)