JIANG Lin (蔣琳) DONG Changming (董昌明) 3 YIN Liping (尹麗萍) 5School of Marine Sciences Nanjing University ofinformation Science and Technology Nanjing 00 ChinaOceanic Modeling and Observation Laboratory Nanjing University ofinformation Science and Technology Nanjing 00China

3Department of Atmospheric and Oceanic Sciences, University of California, Los Angeles, 90095, USA

4First Institute of Oceanography, State Oceanic Administration, Qingdao 266001, China

5Laboratory for Regional Oceanography and Numerical Modeling, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266237, China

AbstractCross-shelf transport is important due to its role in the transport of nutrients, larvae, sediments,and pollutants. The role of coastal trapped waves (CTWs) and their contribution to the cross-shelf transport is presently unknown. The impact of wind-driven CTWs on the structure of the cross-shelf currents and transport is investigated in the East China Sea (ECS) starting from theory. The cross-shelf currents are divided into four terms: the geostrophic balance (GB) term, the second-order wave (SOW) term, the bottom friction(BF) term and Ekman (EK) term, as well as three modes: the Kelvin wave (KW) mode, the fi rst shelf wave(SW1) mode and the second shelf wave (SW2) mode. Comparison among these decompositions shows that(1) for the four terms, the effect of the GB and EK terms is continual, while that of the BF term is confi ned to 60-240 km offshore, and the contribution of the SOW term can be ignored; (2) for the three modes,the KW and SW1 modes are dominant in cross-shelf transport. The results show that the total cross-shelf transport travels onshore under idealized wind stress on the order of 10-1, and it increases along the cross-shelf direction and peaks about -0.73 Sv at the continental shelf margin. With the increase of linear bottom friction coeffcient, the cross-shelf transport declines with distance with the slope becoming more uniform.

Keyword:cross-shelf transport; coastal trapped waves; East China Sea (ECS)

1　INTRODUCTION

In shallow-sea dynamics, many dynamical phenomena occur in the coastal ocean over the continental shelf. Generally, pressure, wind, and precipitation induce sea level oscillations and current changes, which result in pollution transport and sediment resuspension, as well as mass transport over the shelf etc. In winter, Ekman transport and downwelling induced by the monsoons cause sediment to travel from the coast to the central continental shelfin the East China Sea (ECS) (Dong et al., 2011). In the Haizhou Bay nearshore in Jiangsu Province, the pollution diffuses offshore when the wind blows west-southwest (WSW), and accumulates onshore when the wind blows east (E) or eastsoutheast (ESE) (Xie et al., 2008). Simultaneously,onshore transport induced by nonlinear internal waves equals or exceeds offshore Ekman transport, so the internal waves play an important role on the material balance over the continental shelf (Zhang et al., 2015).These previous investigators have typically researched the mass transport on the continental shelf by numerical simulation or moored observations. There are still ambiguities in the theoretical mechanism of the transport on the continental shelf.

Cross-shelf transport can be caused by several physical processes, such as cross-shelf wind (Tilburg,2003; Fewings et al., 2011) and nonlinear internal waves (Zhang et al., 2015). In China seas, the known inducing mechanism of cross-shelf transport includes the northerly monsoonal winds in the Yellow and East China Seas (Yuan and Hsueh, 2010) and nonlinear frontal waves (Liu et al., 2000).

In this paper, we start from the wind-driven coastal trapped waves (CTWs) mechanism to analyze the cross-shelf transport theoretically. CTWs are the hybrid waves with characteristics of both shelf waves and baroclinic Kelvin waves. They are formed along the coast due to the interactions of topography and stratifi cation with the forcing (wind, tide and others)(Gill and Clark, 1974). CTWs can result in lowfrequency sea level fluctuations including generation in remote locations and propagation of the signals into the region (Hamon, 1962). The unidirectional propagation of CTWs along the coast can induce sea level changes of several centimeters (Gill and Schumann, 1974) and interface displacements of tens of meters (Colas et al., 2008). The vertical displacement enables elevation of nutrients into the euphotic zone to supply photosynthesis and profoundly impact primary production and the coastal ecological environment(Echevin et al., 2014). In China, the properties of CTWs in ECS and these waves’ inf l uence on the sea areas have been studied since the 1980s. Using hourly sea level records from tide stations and free CTWs theory, Chen and Su (1987) found free CTWs varied both seasonally and spatially in China seas. Hsueh and Pang (1989) studied the characteristics of wind-driven CTWs under the special double-shelf V-like bottom topography in the Yellow Sea, and pointed out lowfrequency sea-level signals propagating off both the east coast of China and the west coast of Korea. Using the ensemble empirical mode decomposition (EEMD)method, Yin et al. (2014) analyzed the observations from five mooring stations to confi rm the existence of CTWs in the ECS with periods from 2 to 10 days.They found both alongshore wind stress and the curl of wind stress play an important role in the generation of CTWs. In winter 2008, Li et al. (2015) used observations including tidal records, alongshore winds, atmospheric pressure along the China coast, to show that winter storms can excite CTWs along the coast from Zhejiang to Guangdong southerly.

CTWs theory is comparatively well established,however, these researchers concentrate on the analysis of sea level observations and dynamics, and neglect their cross-shelf transport. Though the hindcast of onshore-offshore currents is underestimated based on the present CTWs theory (Brink, 1991), their role still has important theoretical signifi cance. The wide continental shelf of the ECS is ecologically productive.CTWs are one of the primary factors that modify the near-shore currents over the shelf and shelf slope region, and CTWs play an important role in exchanging mass over the shelf (Huthnance, 1995).Weber and Drivdal (2012) found that barotropic CTWs induce the mean Lagrangian drift, which can be subdivided into a Stokes drift and a mean Eulerian drift, and CTWs make a profound inf l uence on transporting biological material and displacing pollution. In this paper, we aim to analyze the crossshelf transport induced by wind-forced CTWs based on the previous studies. The rest of this paper is divided into the following sections: In Section 2, we brief l y introduce the idealized wind-driven CTWs theory. Then we apply this theory to the ECS in Section 3. In an application, involving the study area,application with idealized wind stress and results. The discussion and summary are given in Section 4.

2　CTWS THEORY

Starting with the barotropic, linearized and inviscid shallow-water equation, under the low-frequency and long-wave approximation, i.e. a wave frequency smaller than the inertial frequencythe alongshore scale smaller than the cross-shelf scalethe motion equations in terms of elevation can be reduced to

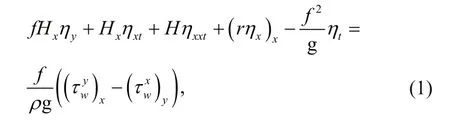
subject to the boundary conditions:

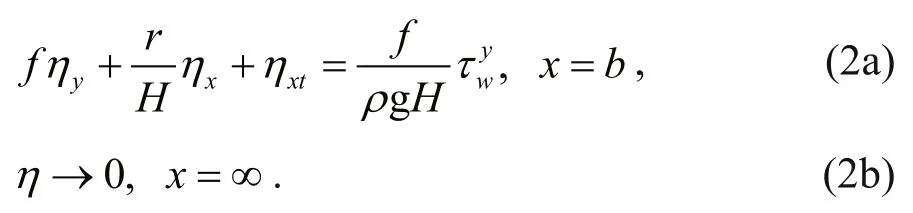
wherexandyare the cross-shelf and alongshore coordinate respectively,tis the time,η(x,y,t) is the sea level change, g is the gravity acceleration,His the water depth,fis the Coriolis parameter (taken as a constant),) is the wind stresses inxandydirections, respectively,r(x) is the bottom friction coeffcient,r(x) can be simplified to be a constant in the calculation, and generally we let it be equal to 3×10-4m/s when considering the weak damping. In Eq.2a,x=bis pretended to be the real coast, the depth of this cross-shelf location is equal to three times the Ekman layer e-folding scaleδ(Clarke and Brink,1985; Mitchum and Clarke, 1986), so this boundary condition indicates that there is no normal flow at the coastx=b, and Eq.2b states that the waves will vanish whenxtends to infi nite area, which means coastal trapping.

The properties of CTWs can be calculated by using a numerical model with realistic bottom topography.Andη(x,y,t) can be divided into a cross-shelf distributionF(x) and an amplitude function?(y,t)which vary along the coast and in time using the separation of variables method (Gill and Schumann,1974)

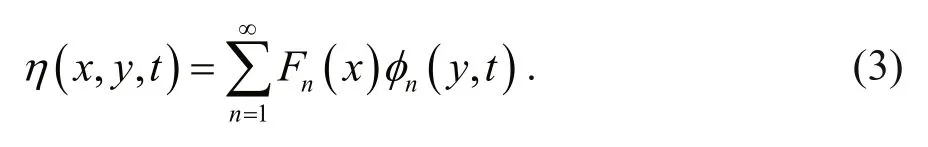
Forced CTWs refer to a group of low frequency waves along the coastal area with the subscriptnrepresenting the wave mode.

The cross-shelf structureFn(x) of the free waves can be solved using the following Sturm-Liouville eigenvalue equation (details see Appendix):

subject to the boundary conditions:

cnis the phase speed of the free wave to moden, and its inverse is also the eigenvalue of this equation(Chapman, 1987).

Amplitude function?(y,t) satisfi es an infi nite set of coupling fi rst-order wave equation according to the numerical method from Clarke and Van Gorder(1986)

where

whereamnrepresent the frictional coupling coeffcient to modemin /m, and the reciprocal ofannprovides the decay distance in the alongshore distance;bnis the wind-coupling coeffcient. Since bottom friction effects are included, idealized winds must not be started abruptly, but phased in. The ramp-up or spinup time is equal tomaxwhich is equivalent to the longest time for the waves of different modes to propagate their frictional decay distance (Clarke and Van Gorder, 1986).

Two steps are required to solve the sea level change. First, we need to solve the cross-shelf structureFn(x) and phase speedcnof the free waves,which is essential to calculate the free wave parameteramn,bn, andγnin Eq.7. Second, the amplitude function,?(y,t), is solved numerically using these parameters.Once the sea level,η(x,y,t), is determined, the corresponding currents can be calculated following:

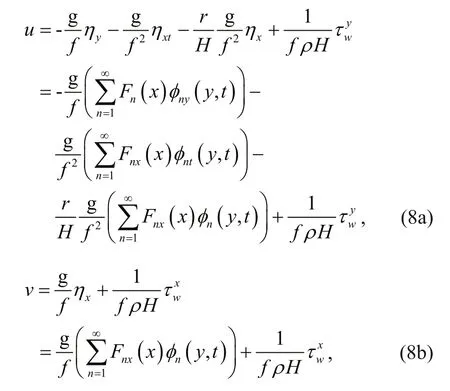
According to Eq.8a, we can calculate the mean cross-shelf volume transport. We denote the mean variable by an over-bar, which is averaged over the wave periodT. Mean cross-shelf seawater volume transportis de fi ned by (unit: Sv, and 1 Sv=106m3/s)

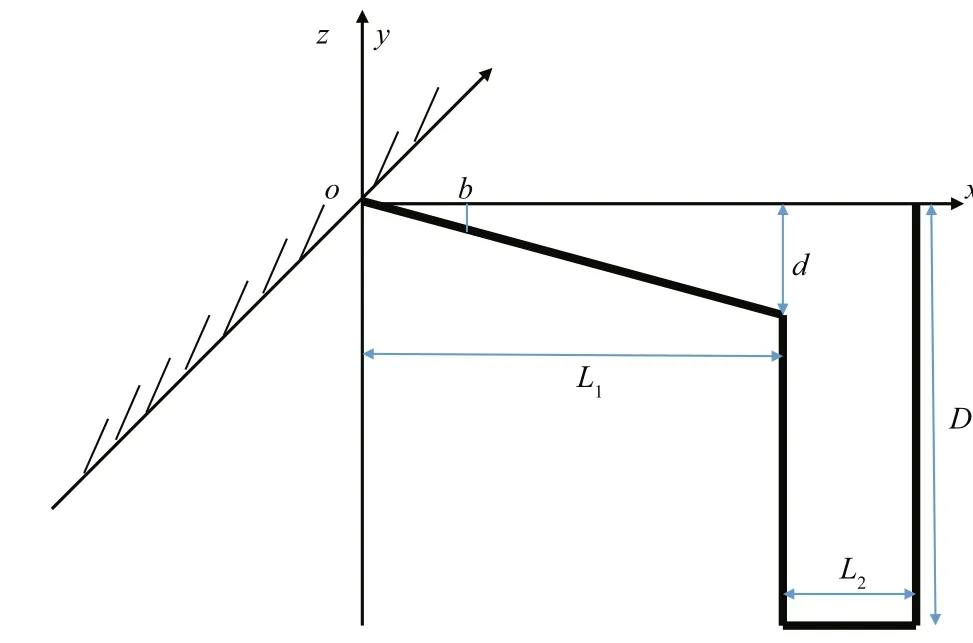
Fig.1　Idealized linearized topographic segmentHereb=60 km,L 1=430 km,L 2=180 km,d=150 m,D=1 600 m. At the locationx=b, the water depth is 21 m, which is equal to three times the Ekman layer e-folding scaleδ. The locationx=bis assumed to be the real coast.

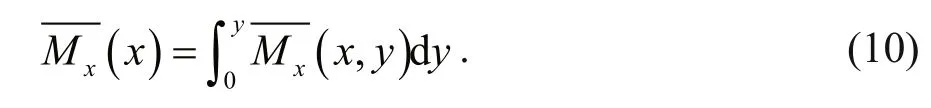
whereMdenotes the seawater volume transport.x

3　CTWS IN EAST CHINA SEA

3.1　Study area

For the area around 29°N, where the Coriolis parameter is approximately equal to 7.0513×10-5/s.The Ryukyu Islands act as the wall in the ECS. We suppose the water depthHdo not change with the straight coasty, and it is only the function ofx. See Fig.1, when the idealized water depthHare piecewise linear functions:

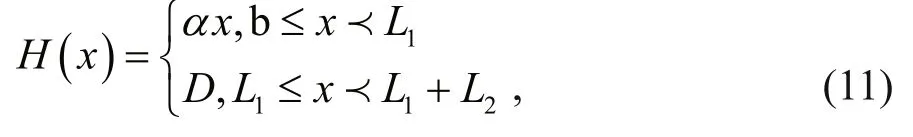
whereα=d/L1, L=L1+L2. And in this fi gure, the crossshelf locationx=bis pretended to be the real coast.Yin et al. (2014) set this water depth at the locationx=bof each segment as 20 m, and here we set this water depth is 21 m. This cross section of the geometry is different from that in Chen and Su (1987), in which coast was set asx=0.

3.2　Application with idealized wind stress

Fig.2　The cross-shelf structure for fi rst three modes of the free waves, i.e. Fn( x) and the amplitudes are normalized with values set to 1 at the coastKW means Kelvin wave mode, SW1 and SW2 mean the fi rst and second Shelf wave respectively.

Affected by the monsoon, the nearshore of the ECS is driven by the north wind during winter. For simplifi cation, we letand=-0.07+0.03cos(l1y+w1t), wherel1=3.64×10-6/m,w1=-3.64×10-5/s. And we set Δy=1 000 m, Δx=1 000 m, and Δt=6 h in numerical calculation. CTWs refer to a group of low frequency waves along a coastal area,however, the selected modes are one of a subset of possible modes. Chapman (1987) pointed out that the higher the modes were more sensitive to the parameters, such as topography and bottom friction etc. This meant more modes could not improve the accuracy of the calculation. For study of the ECS,both Hsueh and Pang (1989) and Yin et al. (2014)believed the fi rst three modes were suffcient to represent the dynamics. Yin et al. (2014) noted that combination of the fi rst three modes replicated 90.3%of what was covered by the fi rst six modes.Consequently, our analysis considers the fi rst three modes. The fi rst three modes of free waveF(x) are shown in Fig.2. The lowest mode is called the KW mode, whose amplitude generally decays exponentially cross the shelf (blue in Fig.2), and its phase speed is the largest, being about 14.3 m/s,which is close to 14.2 m/s in the table of Chen and Su(1987). The second and third modes are known as the shelf waves modes (SW1 and SW2) (green and red in Fig.2, respectively), whose phase speed are 2.9 m/s and 1.02 m/s respectively, which are much smaller than the KW mode, and their amplitudes are different from the KW mode and generally decay in the wave form. In Fig.2,x=430 km is the continental shelf break, and these three modes are almost zero beyond it. The change of the waves is mainly confi ned to the continental shelf. From Table 1, we fi nd the decay distance of SW1 (488 km) and SW2 (176 km) is much shorter than KW (3 548 km). According to max=(-1/cnann), we know the spin-up time is about 69 hour.

Fig.3　The spatial distribution of the cross-shelf transport attributable to GB term (a), SOW term (b), BF term (c) and all terms (d)The positive values represent offshore transport while the negative values represent onshore transport.

Table 1　Free CTWs parameters of fi rst three modes for the topographical profi le as Fig.1

3.3　Result

a) Flow decomposition

For the cross-shelf velocity, we divide it into two components according to Eq.8a. The fi rst component is the interior flow, i.e.and the second component represents the Ekman flow,i.e.The fi rst component is composed of three terms: the geostrophic balance term defi ned aswhich is from the geostrophic balance formula; the second-order wave term de fi ned aswhich represents the geostrophic alongshore velocity over time; the bottom friction term defi ned aswhich is associated with the linear bottom friction coeffcientr.Furthermore, each term can be divided into 3 modes(KW, SW1and SW2) to analyze.

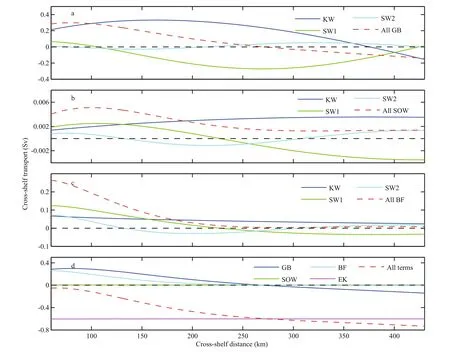
Fig.4　The cross-shelf transport attributable to different modes in GB term (a), SOW term (b) and BF term (c), and the crossshelf transport attributable to different terms (d)The positive values represent offshore transport while the negative values represent onshore transport.

The spatial distribution of the cross-shelf transport attributable to the different terms in Eq.9 is shown in Fig.3. The positive values represent offshore transport while the negative values represent onshore transport.The order of the SOW term (10-3) is much smaller than that of the others (10-1-1), so it can be ignored.The GB term (Fig.3a) continually contributes to the offshore transport, which peaks at the coast, decreasing in magnitude and fi nally switching to onshore transport near about 300 km offshore. The effect of the BF term (Fig.3c) is concentrated within 60-240 km offshore, and the offshore transport decreases with the cross-shelf distance. Figure 3d shows the spatial distribution of the total cross-shelf transport involving 4 terms, which increases along the crossshelf direction. Overall, we fi nd the inf l uence of the BF term is confi ned to 60-240 km offshore, while the contribution of the GB term covers over the whole continental shelf (Fig.3).

The cross-shelf transport attributable to the different modes for each term in Eq.10 is shown in Fig.4. For the GB term (Fig.4a), KW and SW1 are dominant. The offshore transport attributable to the GB term peaks about 0.30 Sv at 81 km, then decays and turns into onshore transport at 376 km. For the GB term, the offshore transport attributable to the KW mode peaks about 0.33 Sv at 165 km, and the onshore transport attributable to the SW1 mode peaks about-0.27 Sv at 269 km. Though the contribution of the SOW term (Fig.4b) can be overlooked, it is also the result of a combination of the three modes. The offshore transport attributable to the BF term (Fig.4c)focuses on the nearshore between 60 and 240 km, and peaks about 0.26 Sv at the coast. In the BF term, the offshore transport induced by the KW mode peaks about 0.07 Sv at the coast and slowly decays to 0.02 Sv. The cross-shelf transport induced by the SW1 and SW2 modes both peak at the coast, about 0.12 Sv and 0.07 Sv, respectively. Figure 4d shows the cross-shelf transport attributable to four terms and the total cross-shelf transport attributable to all terms.Because ofidealized wind stress, the cross-shelf transport induced by the EK term is constant at about 0.60 Sv along cross-shelf distance. The total crossshelf transport (red dotted line) is controlled by the GB, BF and EK term between 60 and 240 km, while the GB and EK terms are dominant from 240 km to the continental shelf margin. The total cross-shelf transport increases along the cross-shelf direction,and peaks about -0.73 Sv at the continental shelf margin.

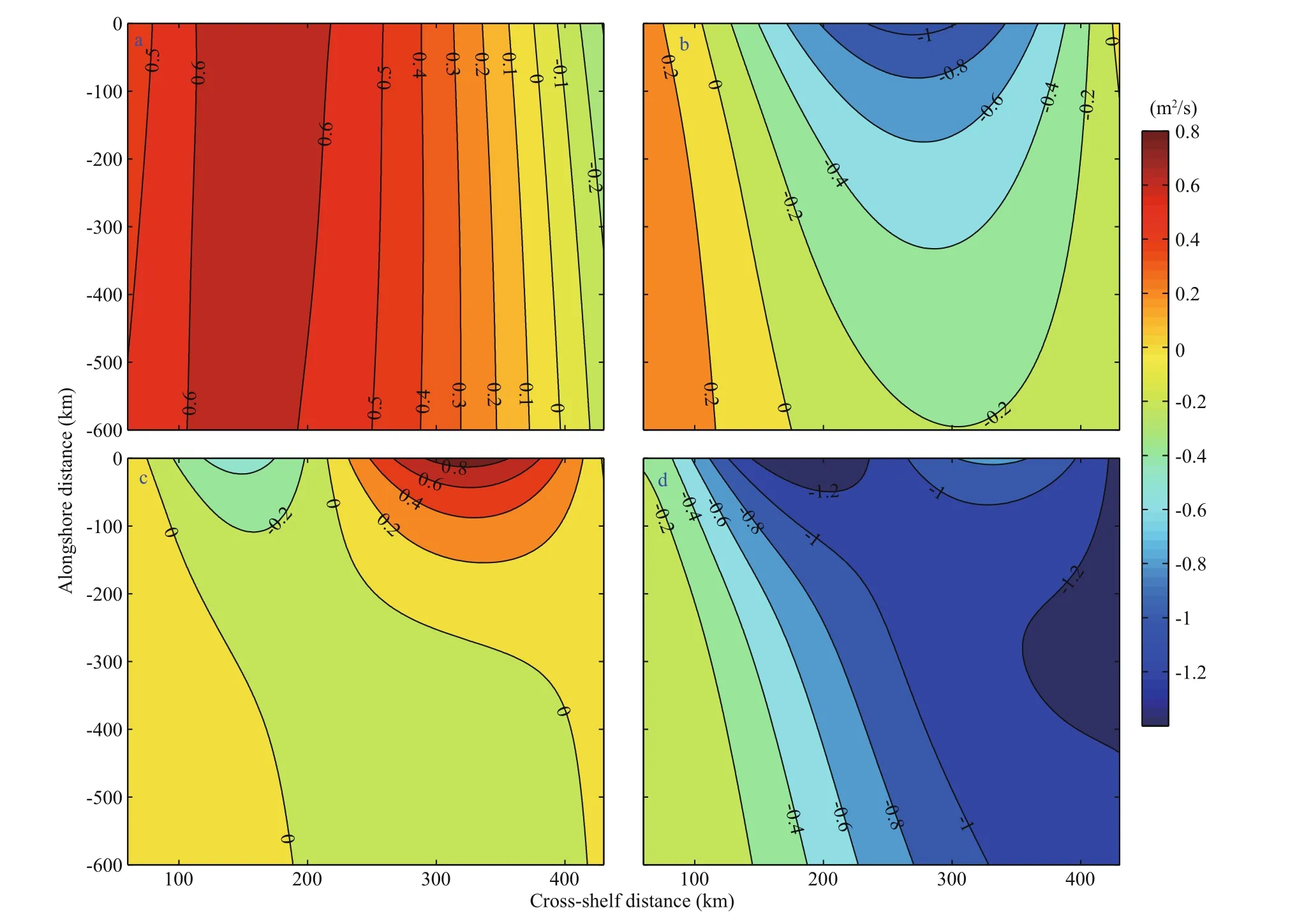
Fig.5　The spatial distribution of the cross-shelf transport attributable to KW mode (a), SW1 mode (b), SW2 mode (c) and all terms (d)The positive values represent offshore transport while the negative values represent onshore transport.

b) Mode decomposition Dividing uIinto three modes, we call

The spatial distribution of the cross-shelf transport attributable to the different modes in Eq.9 is shown in Fig.5. The orders of these three modes are similar. For the spatial distribution, the offshore transport induced by the KW mode (Fig.5a) increases along the crossshelf distance nearshore, and peaks between 100 and 200 km offshore, then slowly decreases in magnitude before fi nally switching to onshore transport near the continental shelf margin. Likewise, the alongshore transport attributable to the KW mode is generally constant in alongshore distance, and this satisfi es that the bottom friction has little effect on the KW mode according to the decay distance of KW (3 548 km).The cross-shelf transport induced by the SW1 mode(Fig.5b) fluctuates along the cross-shelf distance, and the offshore transport decreases along the cross-shelf distance between 60 and 150 km and then changes to the onshore transport. The cross-shelf transport induced by the SW2 mode (Fig.5c) is similar to that induced by the SW1 mode, which has the trend of fluctuation along the cross-shelf distance, and the change is confi ned to the alongshore distance 0-180 km, consistent with the frictional decay distance of the SW2 in Table 1.

Fig.6　The cross-shelf transport attributable to different terms in KW mode (a), SW1 mode (b) and SW2 mode (c), and the cross-shelf transport caused by different modes (d)The positive values represent offshore transport while the negative values represent onshore transport.

The cross-shelf transport attributable to the different terms for each mode in Eq.10 is shown in Fig.6. The effect of the SOW term in each mode is weak, so it can be ignored. This is consistent with Fig.3. For the KW mode, the GB term dominates and fi rst increases peaking with an offshore transport of 0.38 Sv at 158 km offshore, then decreases with distance from the coast starting at 387 km (Fig.6a). In the SW1 mode, the GB and BF terms dominate between 60 and 240 km. After 240 km, solely the GB term controls the flow (Fig.6b). The cross-shelf transport induced by the SW1 mode changes from offshore to onshore at 136 km and peaks in onshore transport at -0.29 Sv at 289 km. For the SW2 mode,the GB and BF terms dominate the cross-shelf transport, which ranges widely from -0.05 Sv to 0.10 Sv (Fig.6c). The cross-shelf transport caused both by three modes and the total including all terms are shown in Fig.6d. Compared with the other two modes, SW2 mode’s contribution to the total crossshelf transport is limited.

c) Sensitivity to bottom friction

Fig.7　The sensitivity test for the mean cross-shelf transport of different bottom friction coeffcients

Wang et al. (1988) pointed out that the decay time of CTWs was about 3 days with bottom friction along the China coast. In this part, we will discuss the effects of different bottom friction coeffcientsron the crossshelf transport. We take 4 different values ofr(0,3×10-4, 6×10-4and 9×10-4m/s) with the outputs shown in Fig.7. In contrast to the other three conditions, the corresponding cross-shelf transport of the conditionr=0 shows declining wave-like fluctuation with two peaks: one at the coast and the other at 180 km. The cross-shelf transport declines with distance with the slope becoming more uniform asrincreases. The cross-shelf transport is generally affected by the bottom topography and the wind stress and energy originates primarily from wind stress, if bottom friction is neglected. However, with bottom friction,the transport is significantly attenuated.

Theoretically, there is no normal flow at the coastal wall (x=b), i.e. the velocities and transport should equal zero, however, this is not true in the results. The number of selected modes is instrumental in determining the normal flow at the wall. As shown in Fig.8, compared with the sum of the fi rst three modes,the results of the sum of the fi rst six modes is closer to 0 at the coast. But the results are similar to when a cross-shelf distance of 90 km is reached and diverge after 430 km. In addition, the results are more sensitive to the parameters due to selecting the higher order of the modes. This calculated error is therefore inevitable.According to the boundary condition of Eq.2a atx=b,the left equation actually include all the modes while the right part just relate to the wind stress, so considering only the fi rst three modes may cause the left value to be slightly smaller than the right value.Further, asrincreases this difference between the two sides becomes smaller until it reaches 0. This is the reason why the transport atx=bis closer to 0 with the increase ofrin Fig.7.

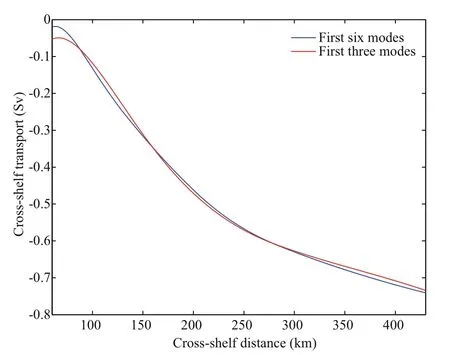
Fig.8　Comparing the effect of the number of selected modes on the cross-shelf transport at the real coast

4　DISCUSSION AND SUMMARY

In this paper, we investigate the role of CTWs in cross-shelf transport theoretically, and discuss the properties of the cross-shelf transport induced by wind-driven CTWs in the ECS in detail. According to the special topography profi le in the ECS, we solve the cross-shelf structure of free waves, phase speed and free waves parameters of CTWs. Based on free waves, we apply the idealized wind stress to hindcast the cross-shelf current produced by wind-driven CTWs, and estimate the cross-shelf transport quantitatively. Assuming a barotropic ocean, this paper approaches the problem from two aspects. One is flow decomposition; the current is composed of 2 kinds of flow, i.e., interior flow and Ekman flow. The interior flow can be further divided into three terms:GB, SOW and BF terms. In other words, there are 4 terms. The other is mode decomposition; the current ofinterior component can be further divided into 3 modes: KW, SW1and SW2 modes.

(1) For the 4 terms, the SOW term can be ignored as it is small on the order of 10-3while others are on the order of 10-1-1. The cross-shelf transport is controlled by the GB, BF and EK term from the coast to the central continental shelf , while the GB and EK term dominate from the central continental shelf to the continental shelf margin.

(2) For the 3 modes, because the decay distance of SW1 and SW2 is shorter than that of KW, the transport distributions produced by these two modes have some limitations in alongshore distance. And the effect of SW2 is weak compared with the other two modes,while the cross-shelf transport is mainly controlled by the KW and SW1 modes.

(3) The results show that the total cross-shelf transport travels onshore under the idealized wind stress on the order of 10-1, and it increases along the cross-shelf direction with the increased gradient decreasing, and peaks about -0.73 Sv at the continental shelf margin.

(4) In the discussion of sensitivity to bottom frictionr, with the increase ofr, the fl uctuating trend of corresponding cross-shelf transport is getting weaker until it becomes approximately a smooth diagonal. And we think the outputs error at the coast,which is not equal to 0, mainly results from the number of selected modes. By comparing two conditions, namely the fi rst three modes and the fi rst six modes, we fi nd that the results of the sum of the fi rst six modes is closer to 0 at the coast than that of the fi rst three modes. But the results are similar in cross-shelf distance 90-430 km.

This paper brought some significant insights on the role of CTWs and their contribution to the cross-shelf transport in the ECS. However, there is still a big gap in the understanding of this new mechanism, thus leaving rooms for more extensive research to be done on the subject, such as making the Coriolis parameter variable instead of constant and bottom friction is quadratic instead of being linear. Therefore, future research work will focus on these two aspects, as well as apply numerical simulations to investigate the cross-shelf transport induced by wind-driven CTWs,while also considering stratifi cation condition.

5　ACKNOWLEDGEMENT

The authors would like to thank Prof. Liang, Prof.Weber, Prof. Wang and Kenny for their kindly help in this work.

We supposeη(x,y,t) can be divided into a cross-shelf distributionF(x) and an alongshore amplitude function?(y,t), i.e.η(x,y,t)=F(x)?(y,t), and we obtain a familiar eigenvalue problem in terms ofF(x) (cis the phase speed of free CTWs andc=w/l):

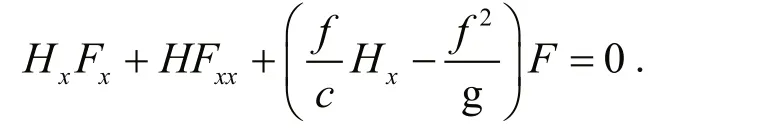
Then see Fig.1, substitute Eq.11 into Eq.4, we can obtain

whereandY0is a Bessel function of the fi rst kind and second kind.A1,A2,B1, andB2are constant coeffcients, which are not zero at the same time. According to the boundary conditionx=bandx=L,and the community conditions ofηandHuat the junction pointx=L1, we can obtain an implicit function of the phase speedc:

Then Eq.A3 can be solved numerically. There are in fi nite number of discrete values ofcn(n=1, 2, …), which have the corresponding free wave modes, i.e.Fn(x).