LIU Jing-huai,SONG Xiao-qiu,ZHANG Li-tao

(1.College of Science,Zhengzhou University of Aeronautics,Zhengzhou 450046,China)

(2.Collaborative Innovation Center,Henan Province for Aviation Economy,Zhengzhou 450046,China)

(3.School of Mathematics,China University of Mining and Technology,Xuzhou 221116,China)

Abstract:This paper is concerned with the existence of square-mean s-asymptotically ωperiodic mild solutions to some stochastic differential equations in a real separable Hilbert space.By using the new theorem of square-mean s-asymptotically ω-periodicity for stochastic process and Banach fixed point theorem,we obtain the existence and uniqueness of square-mean s-asymptotically ω-periodic mild solutions to the equations.To illustrate the abstract result,a concrete example is given.

Keywords: square-mean s-asymptotically ω-periodic;mild solution;stochastic differential equation;Hilbert space

1 Introduction

Recently,some authors studied the theory of s-asymptotically ω-periodic functions with values in Banach spaces and applications to several problems.The concept of sasymptotically ω-periodicity was introduced by Henríquez et al.[1].In[2],Henríquez et al.established the existence and uniqueness theorems of s-asymptotically ω-periodic mild solutions to some classes of abstract neutral functional differential equations with in finite delay.In[3],it was proved that a scalar s-asymptotically ω-periodic function is asymptotically ω-periodic.Nicola et al.[4]provided two examples which show that the above assertion in[3]is false.Since then,it attracted the attention in many publications such as[5–11]and references therein.

Stochastic differential equations attracted great interest due to their applications in many characterizing problems in physics,biology,mechanics and so on.Taniguchi et al.[12]studied the existence,uniqueness and asymptotic behavior of mild solutions to stochastic partial functional differential equations with finite delay.Dorogovtsev et al.[13]proved the existence of periodic solutions to a stochastic equation in a Hilbert space.Bezandry et al.[14]established the existence of square-mean S2-almost periodic solutions of stochastic differential equations and nonautonomous stochastic evolution equations.

Motivated by these works,the main purpose of this paper is to introduce the notion of square-mean s-asymptotically ω-periodicity for stochastic processes and apply this new concept to investigate the existence and uniqueness of square-mean s-asymptotically ω-periodic solutions to the following stochastic differential equations

with

in a real separable Hilbert space,where A:D(A)? L2(P,H)→ L2(P,H)is the in finitesimal generator of a C0-semigroup{T(t)}t≥0on L2(P,H),and{W(t)}t≥0is a Q-Wiener process.Here f,g are appropriate functions specified later and x0is F0measurable.

To the best of our knowledge,the concept of square-mean s-asymptotically ω-periodicity,the existence and uniqueness of square-mean s-asymptotically ω-periodic mild solutions to problems(1.1)and(1.2)in Hilbert space are untreated original problem,which constitutes one of the main motivations of this paper.

The paper is organized as follows:in Section 2,we introduce the notion of squaremean s-asymptotically ω-periodic stochastic process and study some of their basic properties.In Section 3,we give some sufficient conditions for the existence and uniqueness of a square-mean s-asymptotically ω-periodic mild solution to some nonlinear stochastic differential equations in a real separable Hilbert space.In Section 4,an example is given to illustrate our main results.

2 Preliminaries and Basic Results

In this section,we give some definitions and study some of their basic properties which will be used in the sequel.As in[15–17],we assume that(H,‖ ·‖,＜ ·,·＞)and(K,‖ ·‖K,＜·,·＞)are two real separable Hilbert spaces.Let(?,F,P)be a complete probability space.The notation L2(P,H)stands for the space of all H-valued random variables x such that

For x∈L2(P,H),let

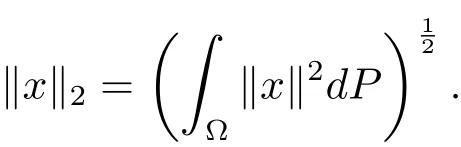
Then it is routine to check that L2(P,H)is a Banach space equipped with the norm ‖x‖2.

The space L2(K,H)stands for the space of all Hilbert-Schmidt operators acting from K into H,equipped with the Hilbert-Schmidt norm ‖ ·‖2.Let K0=and let=L2(K0,H)with respect to the norm

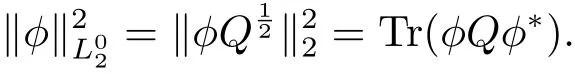
In addition,for a symmetric nonnegative operator Q∈L2(P,H)with finite trace,we assume that{W(t),t≥ 0}is a independent K-valued Q-Wiener process defined on(?,F,P,{Ft}t≥0).

Definition 2.1 A stochastic process x:R→L2(P,H)is said to be continuous in the square-mean sense if

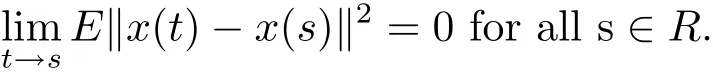
Definition 2.2 Let x:[0,∞)→ L2(P,H)be continuous in the square-mean sense.x is said to be square-mean s-asymptotically periodic if there exists ω＞0 such that

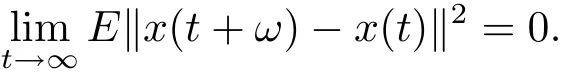
In this case,we say that ω is an asymptotic period of x and that x is square-mean sasymptotically ω-periodic.The collection of all square-mean s-asymptotically ω-periodic stochastic process x:[0,∞)→ L2(P,H)is denoted by SAωP(L2(P,H)).

Definition 2.3 A continuous function f:[0,∞)×L2(P,H)→ L2(P,H),(t,x)→f(t,x),which is jointly continuous,is said to be square-mean uniformly s-asymptotically ωperiodic in t∈[0,∞)uniformly for all x∈K,where K is any bounded subset of L2(P,H),if for any ω ＞ 0,for each stochastic process x:[0,∞)→ K,

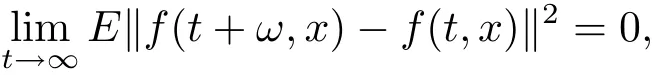
and the set{E‖f(t,x)‖2,t≥ 0,x ∈ K}is bounded.

Theorem 2.4(SAωP(L2(P,H)),‖ ·‖∞)is a Banach space with the norm given by

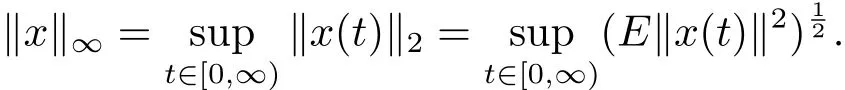
Proof Let{xn}? SAωP(L2(P,H))be a Cauchy sequence with respect to‖·‖∞,xnconverges to x with respect to ‖ ·‖2,that is

for all t≥0.So we need to prove that x∈SAωP(L2(P,H)).

Indeed,for t≥0,we write

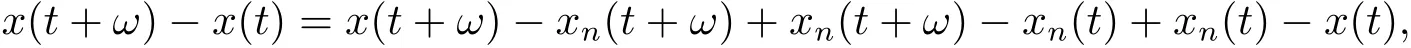
Since(a+b+c)2≤3(a2+b2+c2)for any real number a,b,c,then we get By(2.1)and stochastic continuity of xn,

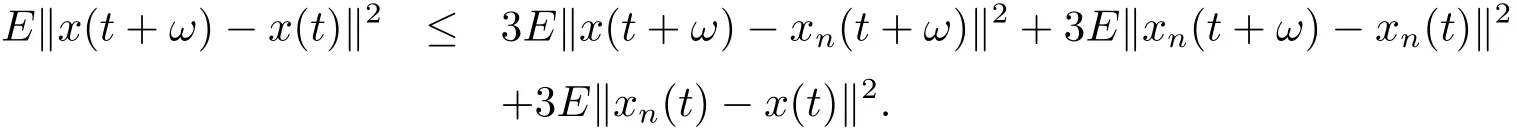
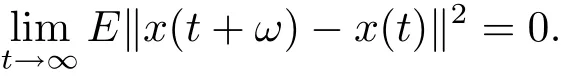
That is x(t)is square-mean s-asymptotically ω-periodic.The proof is completed.

Theorem 2.5 Let f:[0,∞)×L2(P,H)→ L2(P,H)be square-mean uniformly sasymptotically ω-periodic and assume that f(t,·)is asymptotically uniformly continuous on each bounded subset K ? L2(P,H)uniformly for t∈ [0,∞),that is for all∈＞ 0,there exist L∈≥ 0 and δ∈≥ 0,such that E‖f(t,x)? f(t,y)‖2＜ ∈for all t≥ L∈and all x,y ∈ K with E‖x ? y‖2＜ δ∈.Then for any square-mean s-asymptotically ω-periodic process x:[0,∞)→ L2(P,H),the stochastic process F:[0,∞)→ L2(P,H)given by F(·)=f(·,x(·))is square-mean s-asymptotically ω-periodic.

Proof For x∈ SAωP(L2(P,H)),we have

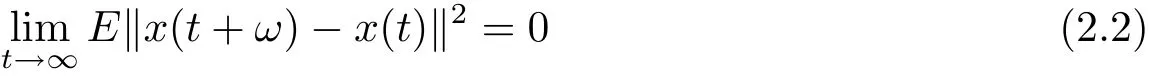
for t ≥ 0.For f is square-mean uniformly s-asymptotically ω-periodic,by Definition 2.3,there exists a bounded subset K?L2(P,H),such that x∈K for t≥0 and we get

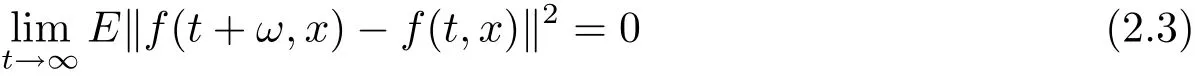
for t≥0 and x∈K.

Note that for t≥0,

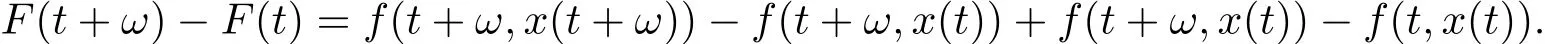
Since(a+b)2≤2(a2+b2)for any real number a,b,so we obtain

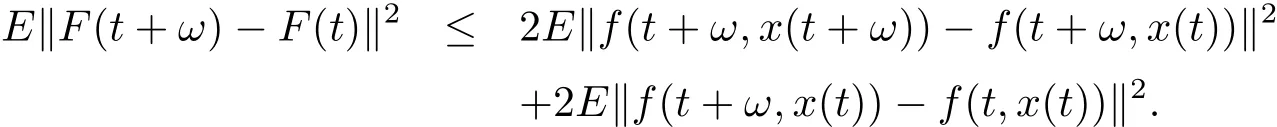
By(2.2)and asymptotically uniform continuity of f(t,x)in x∈K,we have

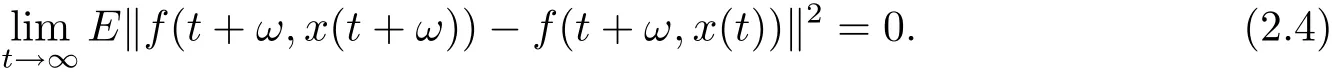
By(2.3),we get

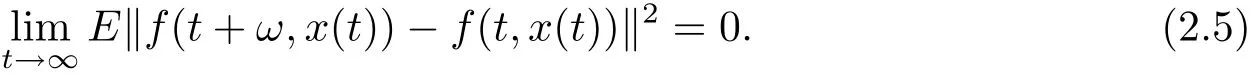
For t≥0,we can deduce from(2.4)and(2.5)that,,which prove that F(t)is square-mean s-asymptotically ω-periodic.The proof is completed.

3 Main Results and Proofs

In this section,we suppose that the following assumptions hold:

(H1)A:D(A)?L2(P,H)→L2(P,H)is the in finitesimal generator of an exponentially stable C0-semigroup{T(t)}t≥0on L2(P,H);that is,there exists constants M ＞ 0 and δ＞ 0 such that‖T(t)‖ ≤ Me?δtfor t≥ 0.

(H2)The function f:[0,∞)×L2(P,H)→ L2(P,H)satisfies the following conditions:

(1)f is square-mean uniformly s-asymptotically ω-periodic and f(·,x)is asymptotically uniformly continuous in every bounded subset K ?L2(P,H)uniformly for t∈[0,∞);

(2)there exists a constant Lf＞0 such that

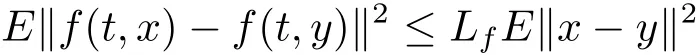
for all x,y∈K and t≥0.

(H3)The function g:[0,∞)× L2(P,H)→ L2(P,L02)satisfies the following conditions:

(1)g is square-mean uniformly s-asymptotically ω-periodic and g(·,x)is asymptotically uniformly continuous in every bounded subset K ?L2(P,H)uniformly for t∈[0,∞);

(2)there exists a constant Lg＞0 such that

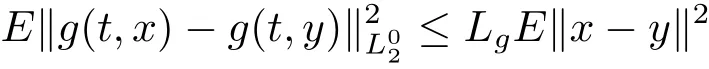
for all x,y∈K and t≥0.

Definition 3.1 Assume that x0is F0measurable.An Ft-progressively measurable stochastic process x(t)is called a mild solution to problems(1.1)and(1.2)if it satisfies the corresponding stochastic integral equation

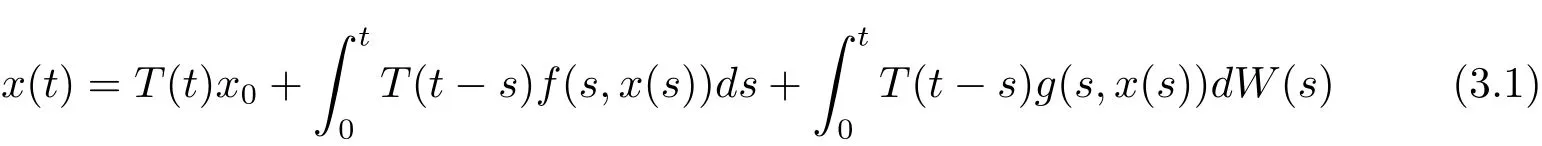
for all t∈ [0,∞).

Throughout the rest of the paper we denote by Γ1,Γ2,the nonlinear integral operators defined by

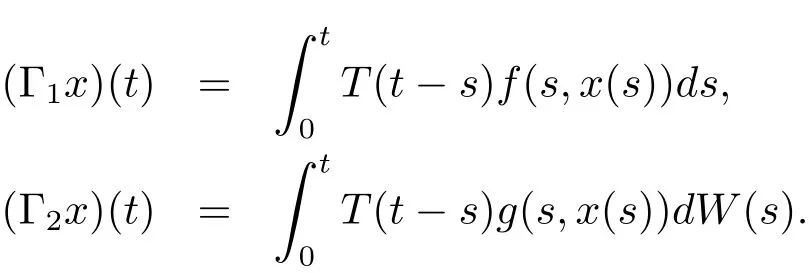
Lemma 3.2 Assume that(H1)and(H2)are satisfied.If x:[0,∞)→ L2(P,H)is square-mean s-asymptotically ω-periodic,then the function Γ1x is square-mean s-asymptotically ω-periodic.

Proof Let x∈ SAωP(L2(P,H)).By(H2)(1)and Theorem 2.5,the function s→f(s,x(s))belongs to SAωP(L2(P,H)).Since F(·)=f(·,x(·)) ∈ SAωP(L2(P,H)),there exists ω＞0,such that

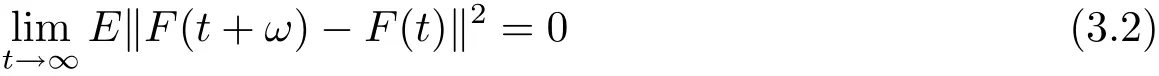
for t≥ 0.Furthermore,for each∈＞ 0,there exists a positive constant L∈such that E‖F(xiàn)(t+ω)?F(t)‖2＜ ∈for every t≥ L∈.Under these conditions,for t≥ L∈,we can write

By using the Cauchy-Schwarz inequality,we have

for t≥0.For F is bounded,then we immediately obtain that

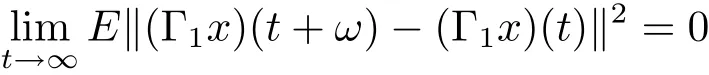
for t ≥ 0.Thus we conclude that Γ1x is square-mean s-asymptotically ω-periodic.This completes the proof.

Lemma 3.3 Assume that(H1)and(H3)hold.If x:[0,∞)→ L2(P,H)is squaremean s-asymptotically ω-periodic,then the function Γ2x is square-mean s-asymptotically ω-periodic.

Proof Let x∈ SAωP(L2(P,H)).By(H3)(1)and Theorem 2.5,the function s→g(s,x(s))belongs to SAωP(L2(P,)).Since G(·)=g(·,x(·)) ∈ SAωP(L2(P,)),there exists ω＞0,such that

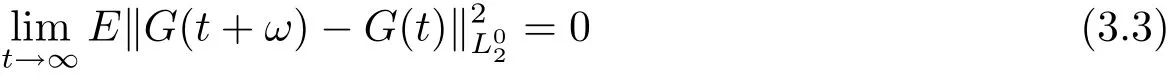
for t≥ 0.Furthermore,for each∈＞ 0,there exists a positive constant L∈such thatfor every t≥ L∈.Let(σ)=W(σ + ω)?W(ω)for each σ ≥ 0.Note thatis also a Brownian motion and has the same distribution as W.Under these conditions,we can write

By using the Cauchy-Schwarz inequality and Lemma 7.2 in[15],we have

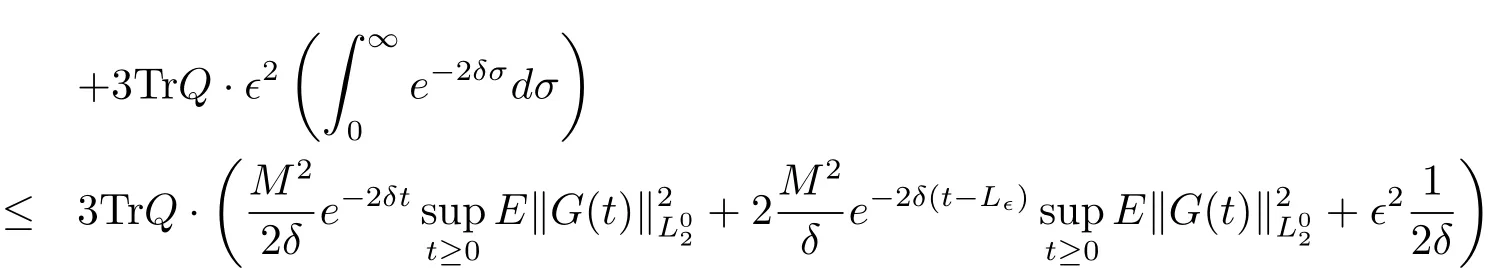
for t≥0.For G is bounded,then we immediately obtain that

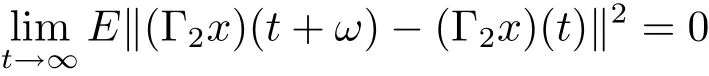
for t ≥ 0.Thus we conclude that Γ2x is square-mean s-asymptotically ω-periodic.This completes the proof.

Theorem 3.4 Assume that assumptions(H1)–(H3)hold.Then the stochastic differential equations(1.1)and(1.2)have a unique square-mean s-asymptotically ω-periodic mild solution whenever Θ is small enough,that is

Proof Define

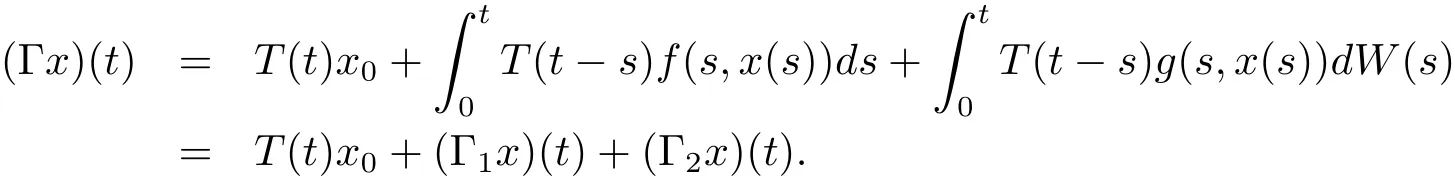
From previous assumptions and the properties of{T(t)}t≥0,one can easily see that T(t)x0→0 as t→ ∞,then the function T(t)x0∈ SAωP(L2(P,H)).By Lemmas 3.2 and 3.3,Γi,i=1,2 maps SAωP(L2(P,H))into itself.To complete the proof,it suffices to prove that Γ has a fixed point.Clearly

Since(a+b)2≤2(a2+b2)for any real number a,b,we get

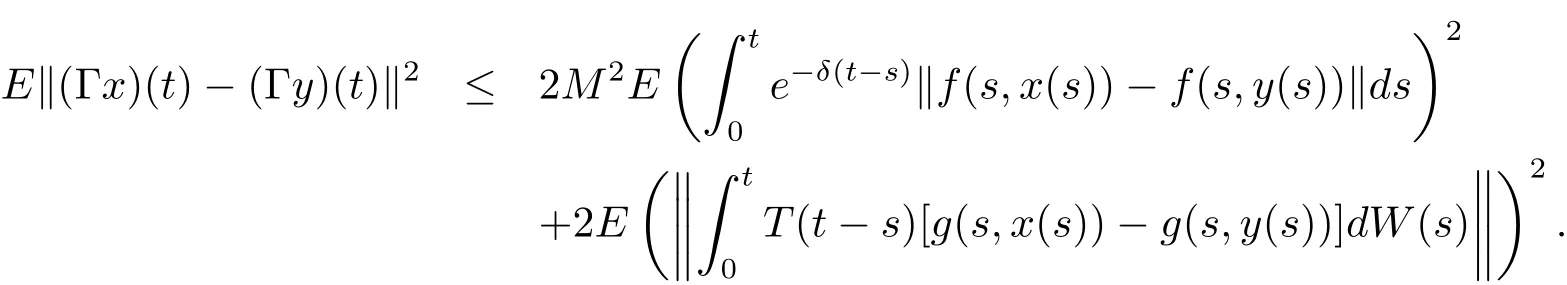
We evaluate the first term of the right-hand side as follows:

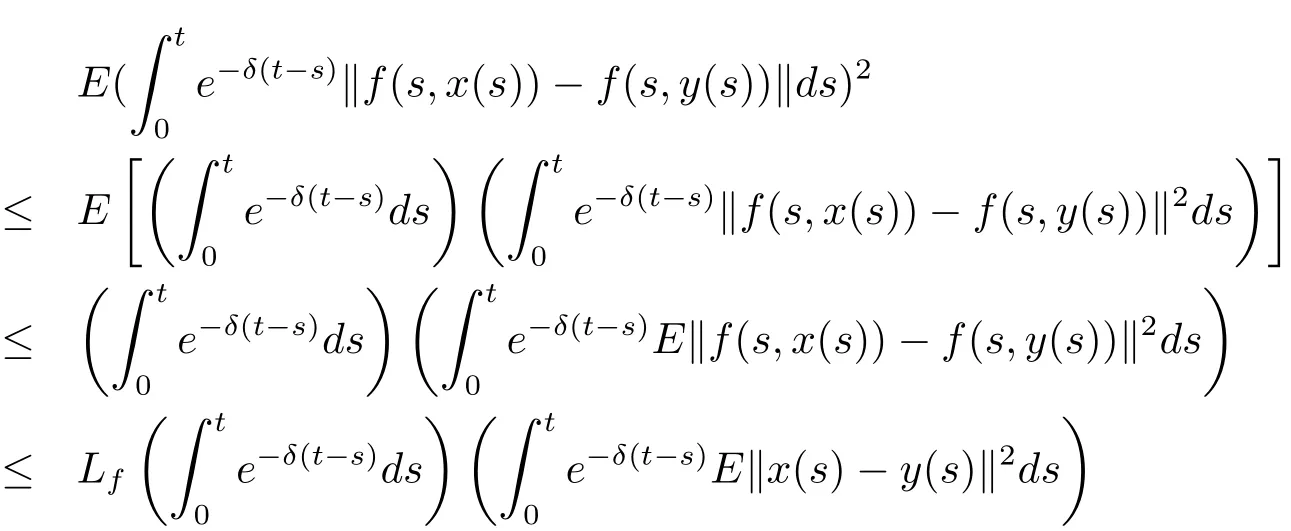
As to the second term,we use again an estimate on the Ito integral established in[15]to obtain

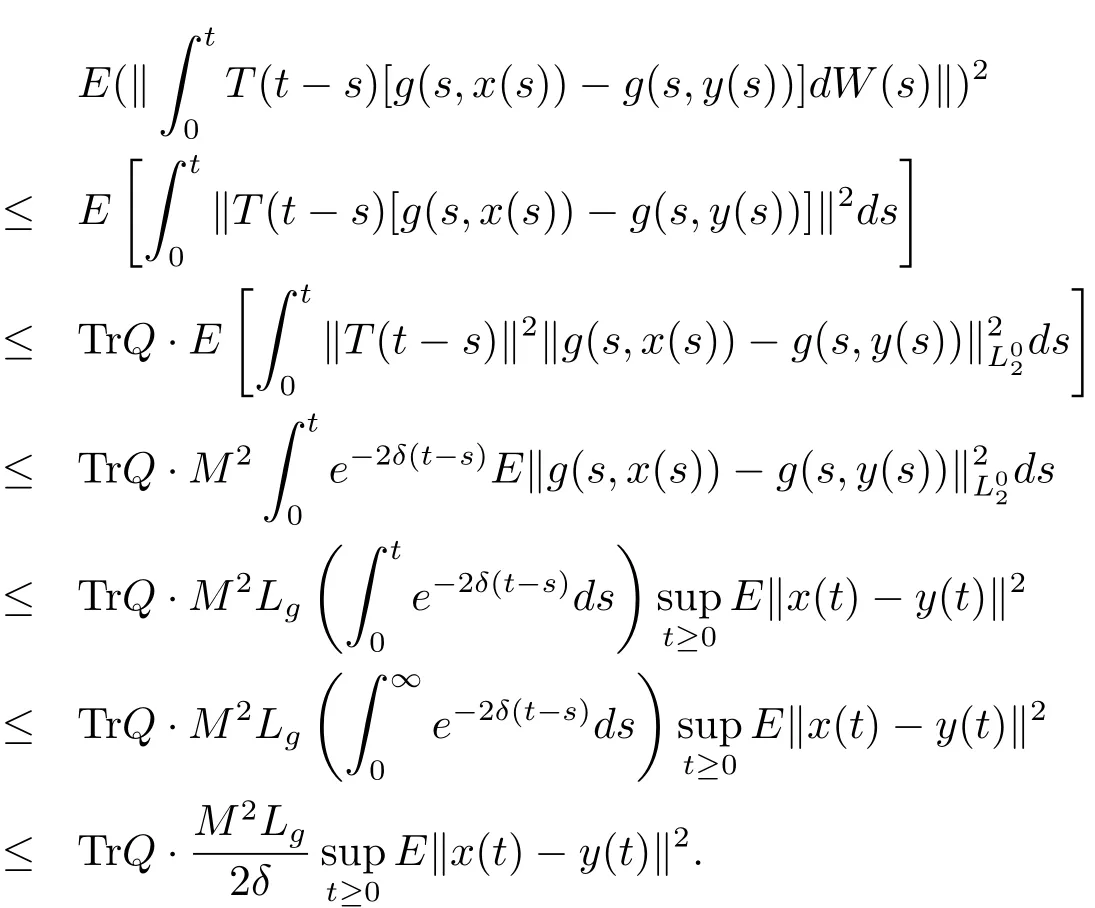
So we have

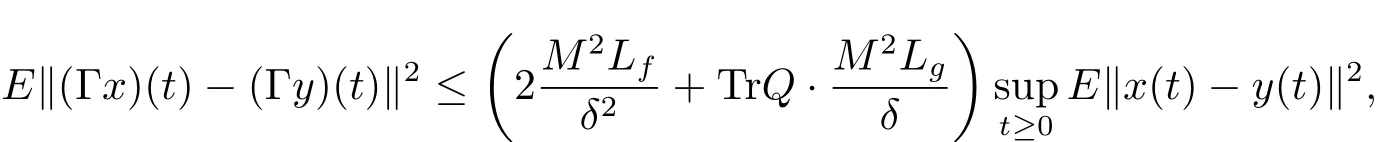
that is

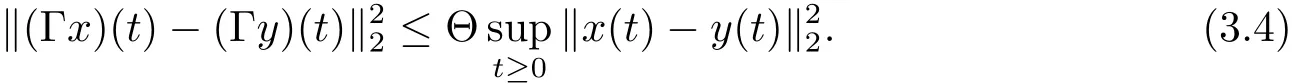
Note that

Hence,by(3.4)and(3.5),for t≥ 0,we obtain

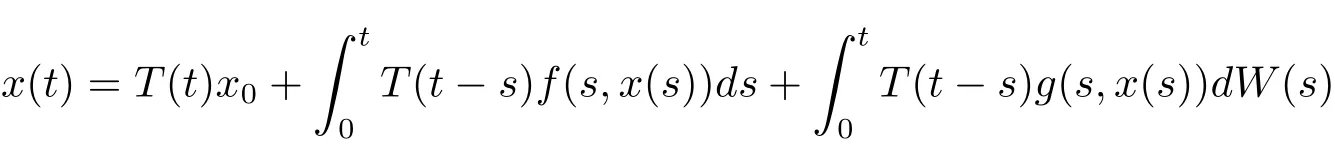
for t≥0.This completes the proof.

4 Example

To complete this work,we consider the existence and uniqueness of square-mean sasymptotically ω-periodic solutions to the stochastic partial differential equation given by the system

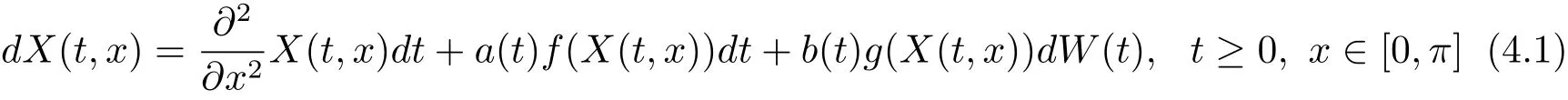
with

and

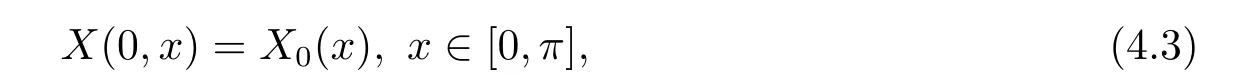
where W is a Q-Wiener process with TrQ＜∞,a(t)=sin(ln(t+1)),b(t)=cos()and f,g are appropriate functions.

Take H=L2([0,π])equipped with its natural topology.The stochastic partial differential equation(4.1)with conditions(4.2)and(4.3)can be written as the following form

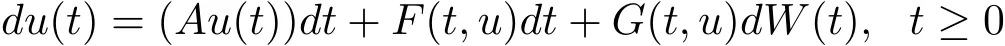
and u(0)=u0,where u(t)=X(t,x)and A is the operator defined by

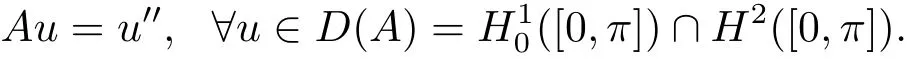
It is well known that A is the in finitesimal generator of an analytic semigroup{T(t)}t≥0and ‖T(t)‖ ≤ e?tfor every t≥ 0.

Assume that there exist constants lf＞0 and lg＞0 such that

for all x,y∈L2(P,H).

Therefore,by Theorem 3.4,the stochastic partial differential equation(4.1)with conditions(4.2)and(4.3)has a unique square-mean s-asymptotically ω-periodic solution whenever lfand lgare small enough.