ZHANG Can,WAN You-yan

(Department of Mathematics,Jianghan University,Wuhan 430056,China)

Abstract:In this paper,the nonlinear Chern-Simons-Schr?odinger systems with exponential nonlinearities are studied.By mountain pass theorem,the existence of a solution to these systems is obtained.

Keywords: Chern-Simons-Schr?odinger systems;exponential nonlinearities;variational methods;mountain pass theorem

1 Introduction and Main Result

We study the existence of solutions to the following Chern-Simons-Schr?odinger system(CSS system)in H1(R2)

where V(x)and f(u)satisfy

(V1)V(x)∈C(R2,R)and V(x)≥V0＞0 for all x∈R2;

(V2)the function[V(x)]?1belongs to L1(R2);

(F1)f∈C(R,R)and f(0)=0;

(F3)there exist θ＞ 6 and s1＞ 0 such that for all|s|≥ s1,

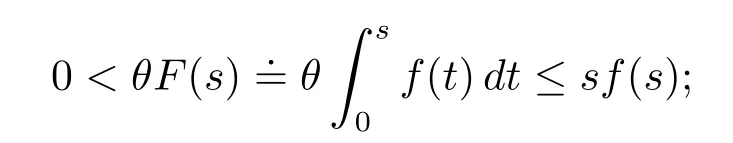
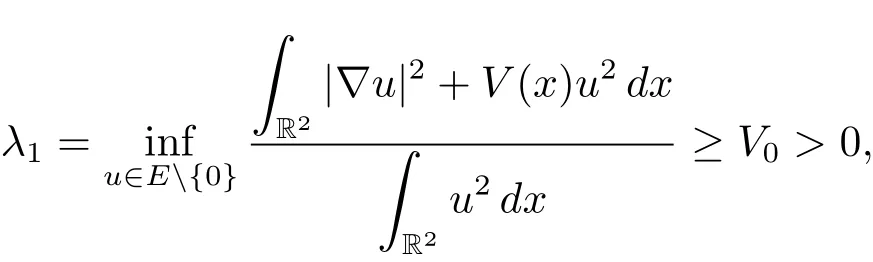
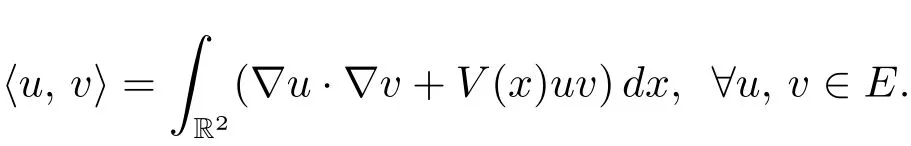
f(u)= λ(2s+s2)esfor 0＜ λ ＜is an example that f(u)satisfies assumptions(F1)–(F4),which was given in[1].

The CSS system received much attention recently,which describes the dynamics of large number of particles in a electromagnetic field.About the detail of its physical background,we refer to the references we mentioned below and references therein.

The CSS system arises from the Euler-Lagrange equations which are given by

This system was proposed in[2–4].Berge,De Bouard,Saut[5]and Huh[6]studied the blowing up time-dependent solutions of problem(1.2)as well as Liu,Smith,Tataru[7]considered the local wellposedness.

We assume that the Coulomb gauge condition ?0A0+?1A1+?2A2=0 holds,then the standing wave ψ(x,t)=eiωtu of problem(1.2)satisfies

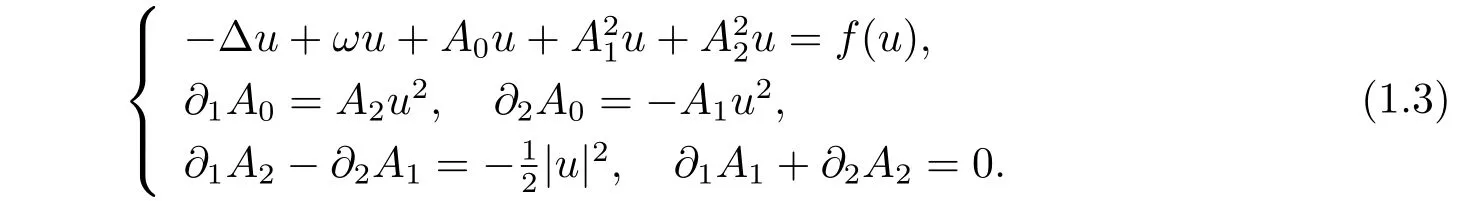
Under some radial assumptions,on the one hand,the existence,non-existence,and multiplicity of standing waves to the nonlinear CSS systems were investigated by[8–12]etc.

On the other hand,the existence of solitary waves was considered by[13–16]etc.For problem(1.1)with f(u)=|u|p?2u,p ＞ 4,without the radial assumptions we mentioned above,by the concentration compactness principle with V(x)is a constant and the argument of global compactness with V ∈C(R2)and 0＜V0＜V(x)＜V∞,the existence of nontrivial solutions to Chern-Simons-Schr?odinger systems(1.1)was obtained in[17].

Inspired by[1]and[17],the purpose of the present paper is to study the existence of solutions for systems(1.1)with exponential nonlinearities.The main difficult of systems(1.1)is that the non-local term Aj,j=0,1,2 depend on u and there is a lack of compactness in R2.Using the mountain pass theorem,we have the following main result.

Theorem 1.1 Suppose(V1),(V2),(F1),(F2),(F3)and(F4)hold,then problem(1.1)has a solution.

This paper is organized as follows.In Section 2 we introduce the workframe and some technical lemmas.In Section 3 we prove the mountain pass construction and(PS)condition,which yields Theorem 1.1.

2 Mathematical Framework

In this section,we outline the variational workframe for the future study.

Let H1(R2)denote the usual Sobolev space with

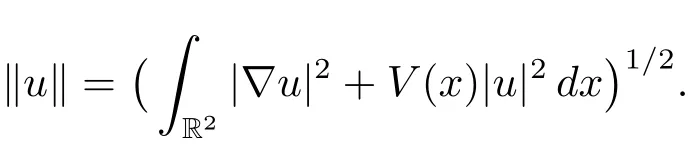
We consider the following subspace of H1(R2),

Condition(V1)implies that the embedding E→H1(R2)is continuous.Assumption(V2)and H?older inequality yield that

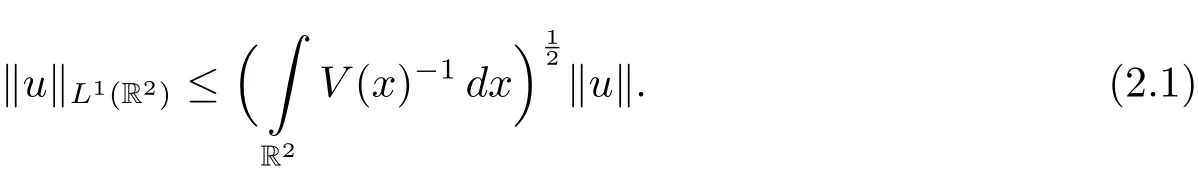
Consequently,

are continuous.Furthermore,by condition(V2),the above embeddings are compact(see[18,19]).

Define the functional

We have the derivative of J in H1(R2)as follows

By(1.1),we have that Ajsatisfy

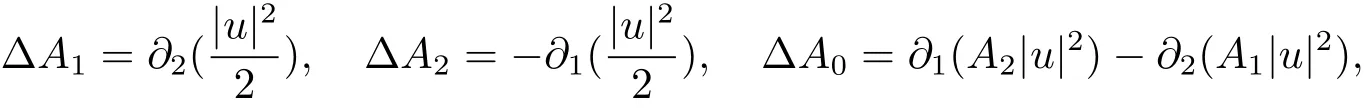
which provide

We know that J is well defined in H1(R2),J∈C1(H1(R2)),and the weak solution of(1.1)is the critical point of the functional J from the following properties.

Proposition 2.1(see[17])Let 1＜s＜2 and

(i)Then there is a constant C depending only on s and q such that

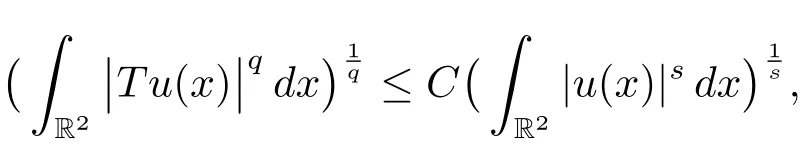
where the integral operator T is given by

(ii)If u ∈ H1(R2),then we have that for j=1,2,and

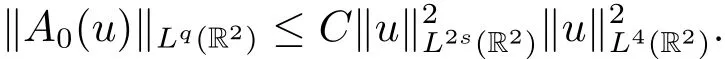
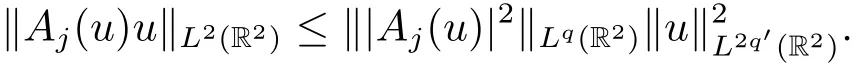
We will use the following mountain pass theorem to obtain our main result.

Theorem 2.2(see[20])Let E be a real Banach space and suppose that I∈C1(E,R)satisfies the following conditions

(i)I(0)=0 and there exist ρ ＞ 0,α ＞ 0 such that I?Bρ(0)≥ α;

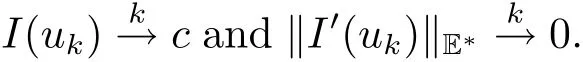
Moreover,if I satisfies(PS)condition,then c is a critical value of I in E.

The following result on Aj,j=0,1,2 is important to prove the compactness.

Proposition 2.3(see[17])Suppose that unconverges to u a.e.in R2and unconverges weakly to u in H1(R2).Let Aj,n:=Aj(un(x)),j=0,1,2.Then

In order to prove the mountain pass construction,we need the following results in[1,21,22].

Proposition 2.4 (i)If α ＞ 0 and u∈ H1(R2)then.Moreover,ifand α ＜ 4π,then there exists a constant C=C(M,α)such that

(ii)Let β ＞ 0 and r ＞ 1.Then for each α ＞ r there exists a positive constant C=C(α)such that for all s ∈ R, eβs2? 1r≤ Ceαβs2? 1.In particular,if u ∈ H1(R2),thenbelongs to L1(R2).

(iii)If v ∈ E,β ＞ 0,q ＞ 0 and ‖v‖≤ M with βM2＜ 4π,then there exists C=C(β,M,q)＞ 0 such that

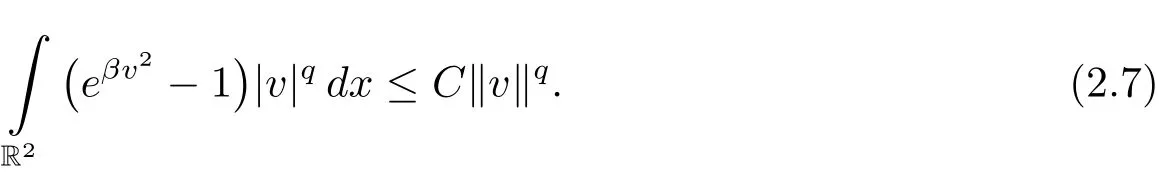
3 Proof of Main Theorem

First of all,we prove the mountain pass structure.

Lemma 3.1 Assume(F2),(F3),and(F4)hold.Then there exist ρ ＞ 0,α ＞ 0 such that J(u)＞ α for all‖u‖= ρ.

ProofFrom(F4),there exist ε,δ＞ 0,such that

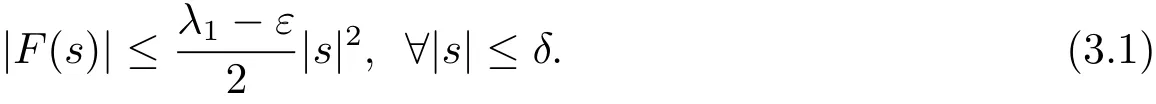
By(F2)and(F3),we have?q＞ 2,there exists C=C(q,δ)such that

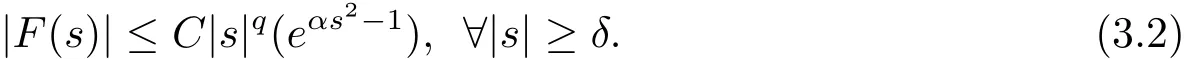
By(3.1)and(3.2),we have

From(iii)of Proposition 2.4,the definition of λ1,and the continuous embeddings(2.2),we obtain

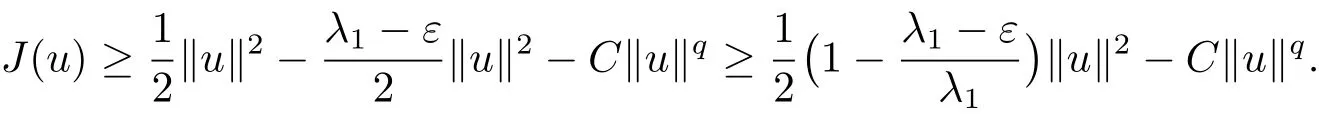
Hence,we have

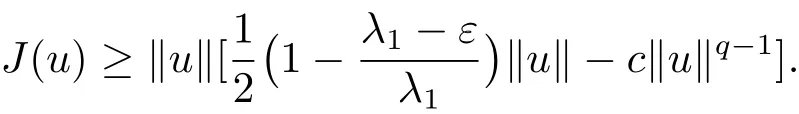
By ε＞ 0 and q ＞ 2,we can choose ρ ＞ 0 and α ＞ 0 such that J?Bρ(0)≥ α ＞ 0.

Lemma 3.2 Assume that f satisfies(F3).Then there exists e∈ E with ‖e‖ ＞ ρ such that J(e)＜0.

Proof Let u∈H1(R2)such that u≡s1in B1,u≡0 inand u≥0.Define k=supp(u).From(F3),there exist positive constants C1,C2such that for all s∈R,

Then we have for t＞1,

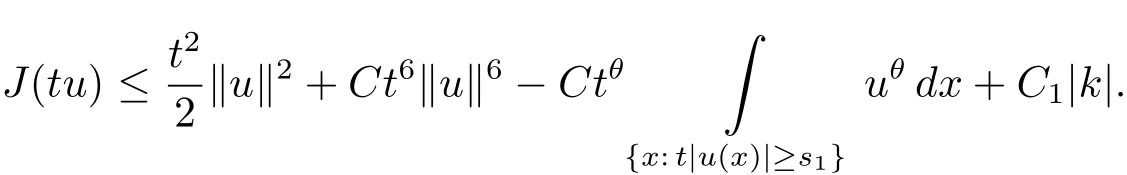
Since θ＞ 6,we have J(tu)→ ?∞ as t→ +∞.Let e=tu with t sufficiently large,the proof is completed.

By Theorem 2.2,the functional J has a(PS)csequence.Next,we show this(PS)csequence is bounded.

Lemma 3.3 Assume(F2)and(F3)hold.Let(un)is a(PS)csequence of J in E,that is,J(un)→ c and J′(un)→ 0.Then ‖un‖ ≤ C for some positive constant C.

ProofWe know

and for any ?∈E,we have

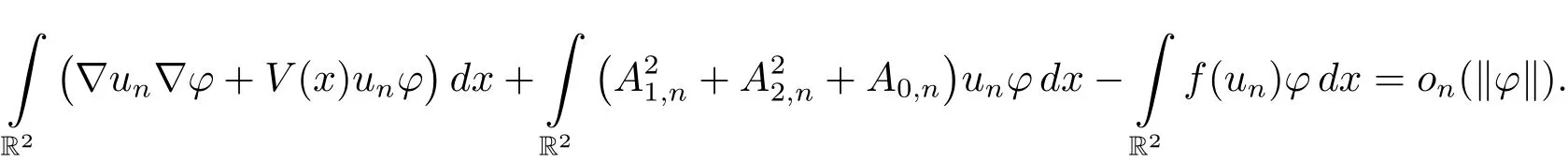
By(F3)and θ＞ 6,we get

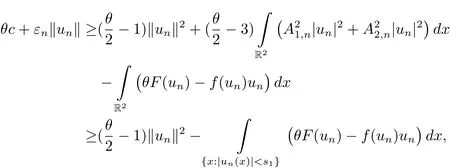
where εn→ 0 as n → ∞.From|f(s)s?F(s)|≤ c1|s|for all|s|≤ s1and inequality(2.1),we obtainwhich implies that‖un‖ ≤ C.

Now we are going to prove(PS)condition.

Lemma 3.4 The functional J satisfies(PS)condition.

Proof Let{un}be a(PS)csequence of J,that is,J(un) → c and J′(un)=0.By Lemma 3.3,{un}is bounded,up to a subsequence,we may assume that un?u0in E,un→u0in Lq(R2)for all q≥1 and un→u0almost everywhere in R2,as n→∞.If f(s)satisfies(F2)and(F4),we have for each α＞0,there exist b1,b2＞0 such that for all s∈R,

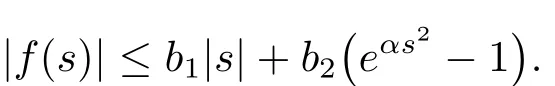
Then we have

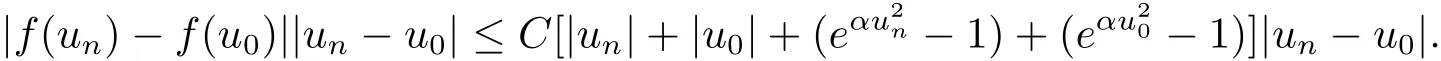
By(i)and(ii)of Proposition 2.4 and H?older inequality,we obtain

By Proposition 2.3,we have

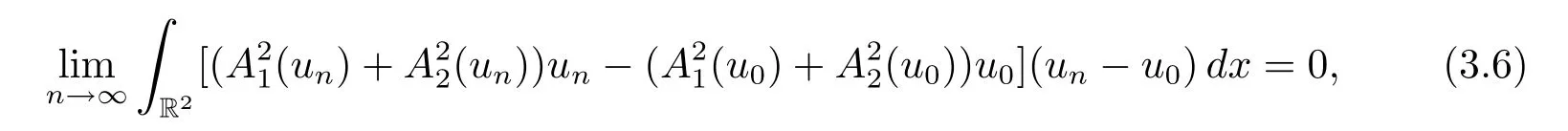
and

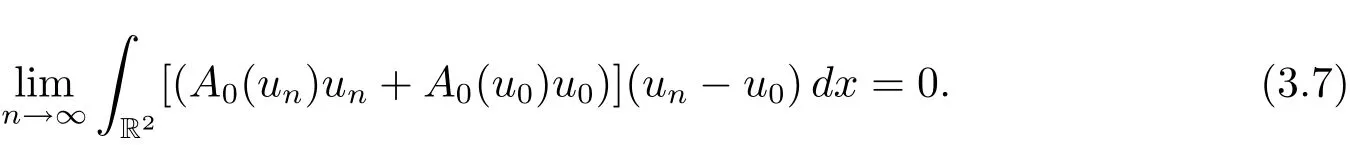
From(3.5),(3.6),and(3.7),we have We obtain that un→u0as n→∞in E.

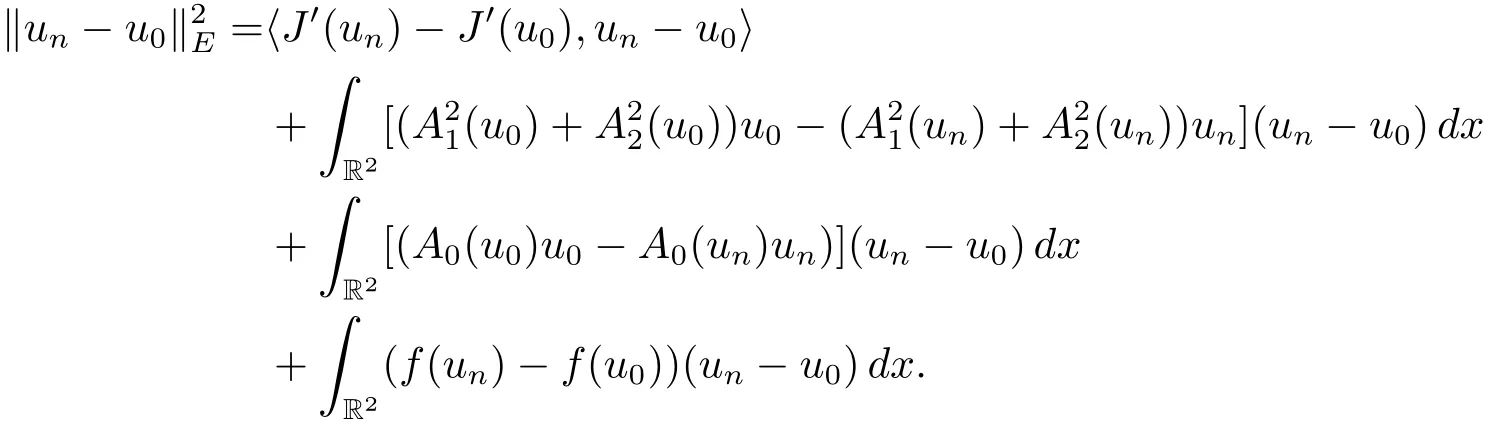
Proof of Theorem 1.1 By Theorem 2.2,Lemma 3.1,Lemma 3.2 and Lemma 3.4,we obtain that functional J has a critical point u0at the minimax level

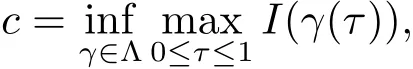
where Λ ={γ ∈ C([0,1],E):γ(0)=0,γ(1)=e}.