邵新慧, 張振鐸

(東北大學(xué) 理學(xué)院, 遼寧 沈陽 110819)

現(xiàn)代很多領(lǐng)域在實際發(fā)展中,矩陣計算和方程組求解已經(jīng)成為不能回避的核心重要問題.往往在特定的學(xué)科和環(huán)境下,特殊矩陣的分析和計算突顯出重要的地位.本文討論的Toeplitz矩陣在數(shù)字信號處理,流體力學(xué)中就有極其廣泛的應(yīng)用,因此尋找Toeplitz矩陣線性方程組的快速算法就顯得尤為重要[1-2].較早的求解方法,主要將精力放在直接方法上,且成果顯著,復(fù)雜度為O(n3),Toeplitz矩陣由2n-1個元素決定,所以研究者希望得到更低復(fù)雜度的算法[3].后來,迭代法成為研究重點,有研究者試圖通過分裂Toeplitz矩陣從而迭代求解線性方程組[4-8].這一思路較早的應(yīng)用是Bai提出的HSS方法[9].很多學(xué)者也在文獻[9]基礎(chǔ)上又給出了一些改進方法[10-12].后來,Micheal.K.G針對Toeplitz矩陣的特殊結(jié)構(gòu),提出了CSCS方法[13],即將Toeplitz矩陣分裂成一個循環(huán)和一個反循環(huán)矩陣,再進行雙步迭代求解.而后,在2013年,N.Akhondi和F.Toutounian提出了加速CSCS方法,即ACSCS[14],它是在CSCS方法上,將單一參數(shù)形式改進成為了雙參數(shù)的形式,在理論和實驗結(jié)果上,都取得了較好的結(jié)果.最新相關(guān)Toeplitz系統(tǒng)求解的研究進展,在一些文獻中提到[15].

本文在Micheal.K.G給出的CSCS方法基礎(chǔ)上,提出了新的算法,稱其為改進復(fù)參數(shù)CSCS方法,并將計算范圍推廣至復(fù)數(shù)域并引入兩個不同的復(fù)參數(shù)進行分裂計算,并給出了新方法的理論分析證明.數(shù)值算例的結(jié)果表明新方法優(yōu)于之前的算法.

1 CSCS算法及其改進算法

對于給定的Toeplitz矩陣的n×n階方程組Ax=b.其中

是Toeplitz矩陣.Toeplitz矩陣A具有循環(huán)和反循環(huán)分裂A=C+S,其中:

這里C是循環(huán)矩陣,S是反循環(huán)矩陣.由此,提出了一種基于循環(huán)/反循環(huán)分裂迭代的非Hermitian Toeplitz系統(tǒng)的迭代Toeplitz求解法(CSCS迭代)如下:

CSCS迭代方法:給定初始假定x(0),對于k=0,1,2,…直到{x(k)}收斂,計算:

這里α是正常數(shù).

理論證明,若C和S都是正定的矩陣,CSCS方法將收斂到唯一解.

基于Michael K.Ng的CSCS方法,在2012年,N.Akhondi和F.Toutounian提出了加速循環(huán)與反循環(huán)分裂法,即ACSCS方法.此方法中將CSCS方法中的單參數(shù)迭代形式,改為了雙參數(shù)的迭代形式:

ACSCS方法具體如下.

給定初始假定x(0),對于k=0,1,2,…直到{x(k)}收斂,計算:

其中α為給定的非負常數(shù),β為正常數(shù).

理論分析表明,如果有效矩陣A是Hermitian正定的,且β在適當(dāng)?shù)膮^(qū)域被限制,對于任何給定非負α的線性系統(tǒng),ACSCS迭代可以收斂到的唯一解.ACSCS迭代的收斂因子的上限取決于α,β以及循環(huán)矩陣C的譜和反循環(huán)矩陣S.理論上,ACSCS的收斂速度是O(nlongn).在實際的數(shù)值實驗中,ACSCS方法的效率優(yōu)于CSCS方法.

與之前不同的是,對Toeplitz矩陣A進行循環(huán)和反循環(huán)分解時,為了保障矩陣C和S的正定性,對A的分裂形式進行了調(diào)整.在這里C和S的推廣形式如下:

其中0<β<1.

矩陣A可以做下面形式的分解:

(3)

其中,α=θ1+η1i,β=θ2+η2i,(θ1>0,θ2>0,η1≥0,η2≥0),矩陣C和S滿足式(1)和式(2).

迭代格式如下:給定初始假定x(0),對于k=0,1,2,…直到{x(k)}收斂,計算:

其中:I是n階單位陣;α,β和矩陣C,S均在式(3)中說明.

引理1[9]令A(yù)∈Cn×n,A=Mi-Ni(i=1,2)是矩陣A的雙步分裂,x(0)∈Rn是給定的初始向量,如果{x(k)}是一個雙步迭代序列,且滿足

那么

定理1 令矩陣A∈Cn×n是一個Toeplitz矩陣,C和S分別為循環(huán)矩陣和飯循環(huán)矩陣,滿足A=C+S,α=θ1+η1i,β=θ2+η2i,(θ1>0,η1≥0,θ2>0,η2≥0).如果C和S是正定的,那么改進CSCS方法的參數(shù)符合下面的限制

則有ρ(M(α,β))<1.此時對于給定的初始向量x(0)∈Rn,迭代序列{x(k)}都收斂于方程的精確解.

證明 由式(4),代入迭代陣,有下式

則,迭代矩陣的譜有下上限

其中

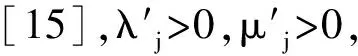
可以保證ρ(M(α,β))<σ(α,β)<1,即新算法收斂.

2 數(shù)值算例

以下例子均是針對(3-1)形式的Toeplitz方程組,其中的系數(shù)和常數(shù)矩陣均是計算機隨機生成,迭代終止準(zhǔn)則均為

首先給出一個小例子簡單展示出改進復(fù)參數(shù)CSCS方法在計算復(fù)數(shù)域Toeplitz時的效率.

例1 對于5階Toeplitz矩陣方程組

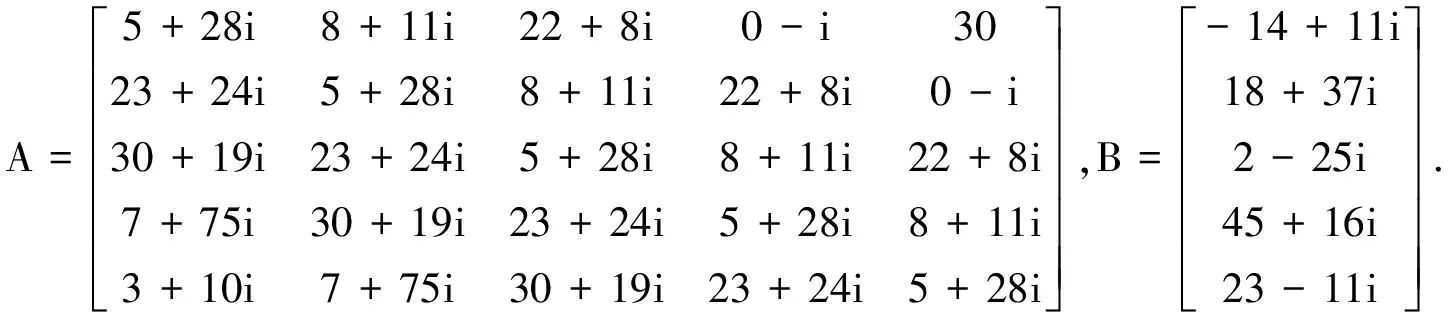
在這里先考慮是傳統(tǒng)的CSCS方法.當(dāng)兩個參數(shù)相同,取不同值時的計算迭代情況.

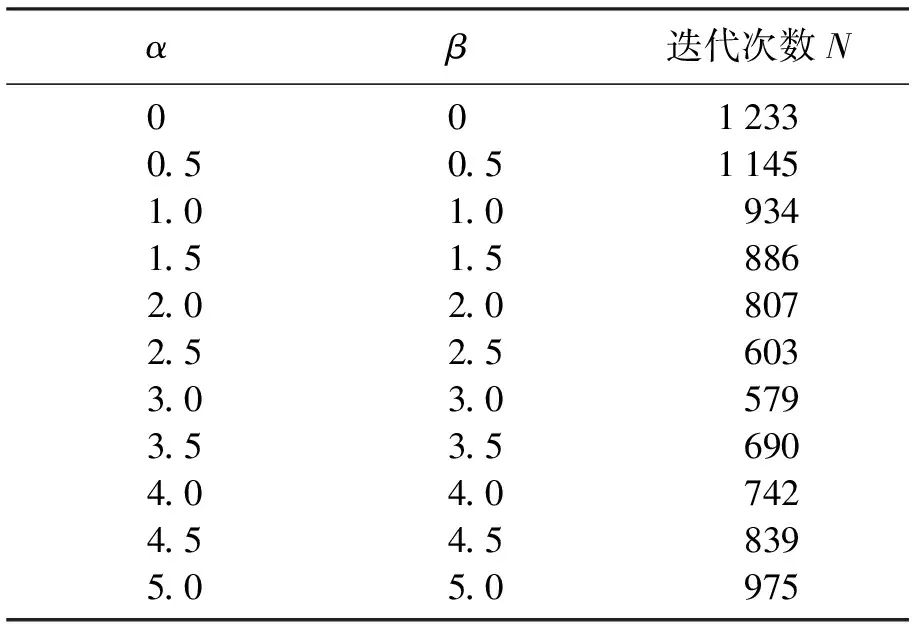
表1 傳統(tǒng)CSCS方法1Table 1 Traditional CSCS method 1

可見,當(dāng)參數(shù)達到3左右時達到了最佳的計算效果,579步左右.下面將展示改進復(fù)參數(shù)CSCS方法的計算結(jié)果,其中參數(shù)的實部選取的并不是傳統(tǒng)CSCS最佳的參數(shù)3,而是選擇的2,最后將看到再適當(dāng)選擇復(fù)數(shù)部時,最佳效果將優(yōu)于傳統(tǒng)CSCS選取最佳參數(shù)時的結(jié)果.

比較當(dāng)α=β=2+0.1i時和α=2+0.17i,β=2+0.1i時, 可以清楚的看到改進算法的效果, 即雙參數(shù)較之單參數(shù)的效率提高, 并且在后者情況, 計算步數(shù)在實部不變的情況下達到了最小值.

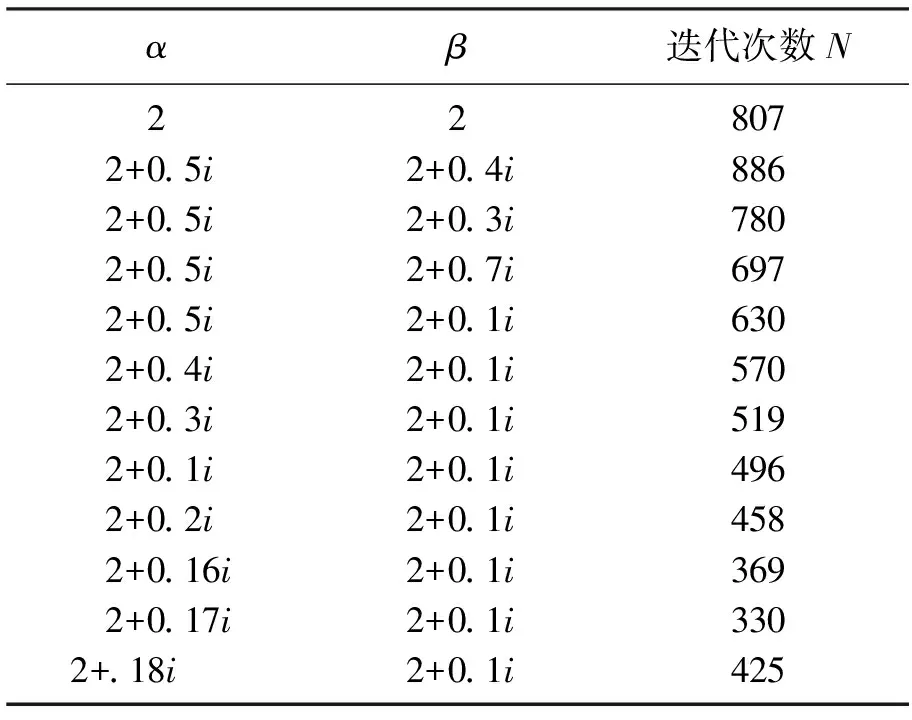
表2 改進復(fù)參數(shù)CSCS方法1Table 2 Improved complex parameters CSCS method 1

可見,即使實部選取不是傳統(tǒng)CSCS方法最優(yōu)的參數(shù),改進CSCS方法也可以得到優(yōu)于傳統(tǒng)CSCS的結(jié)果,最優(yōu)達到了330步,較之前有579步有很大提高.

同時,也可以看到在實部不變的情況下,隨著虛部的調(diào)整,迭代步數(shù)明顯的變少,這說明引入復(fù)參數(shù)確實增加了計算效率.

例2 對于7階Toeplitz矩陣方程組

事實上,適當(dāng)選取參數(shù)的實部可以大大提高計算效率.在本例中將說明這一點.下面是不同參數(shù)選擇時的迭代情況.

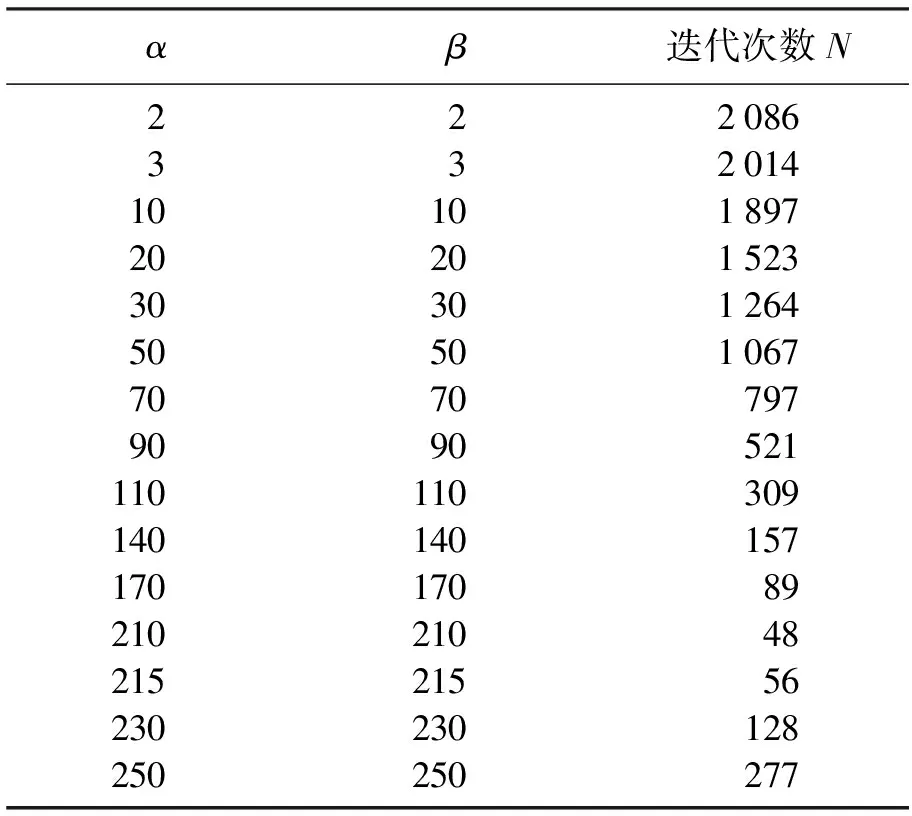
表3 傳統(tǒng)CSCS方法2Table 3 Traditional CSCS method 2

可見,當(dāng)參數(shù)選取210時,計算效率達到了最佳,細致的參數(shù)選擇對計算影響很大.下面將展示改進復(fù)參數(shù)CSCS方法,

這里的參數(shù)實數(shù)部分將選擇傳統(tǒng)CSCS方法的最優(yōu)參數(shù)210.

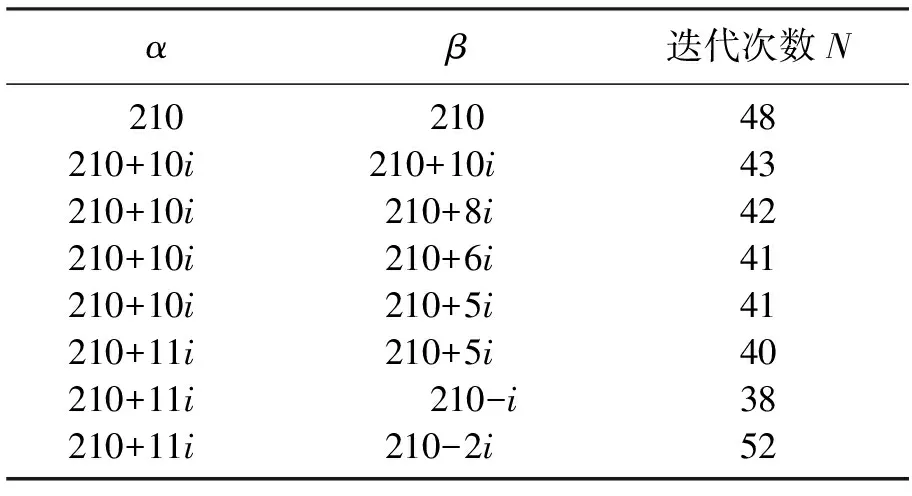
表4 改進復(fù)參數(shù)CSCS方法2Table 4 Improved complex parameters CSCS method 2

首先可以明顯的看出實數(shù)部選擇對計算效率的影響,事實上,通過調(diào)試,當(dāng)兩個參數(shù)取210是傳統(tǒng)CSCS方法能達到最快時的取值,由于此討論不是本文重點,在此做出說明即可.

當(dāng)實部取最優(yōu)參數(shù)時,通過調(diào)整虛數(shù)部分依然可以有效提高計算效率.改進的復(fù)參數(shù)CSCS方法較之前的方法從48步提高到了38步,效率提高了20%.

以上例子說明,在求解復(fù)數(shù)域Toeplitz系統(tǒng)時,改進CSCS方法是確實有效且快速的.

4 總結(jié)與展望

回顧了CSCS算法的同時提出了改進的算法,新算法能夠適應(yīng)更廣泛種類的矩陣,而不是同傳統(tǒng)的CSCS算法一樣只用于實矩陣,這樣的方法有廣泛的實用性.由于參數(shù)可以調(diào)節(jié),而不是原有的一個參數(shù)的類型,這提高了算法的效率,且具有較好的穩(wěn)定性.

綜上所述,改進后的CSCS算法有著比傳統(tǒng)CSCS算法更好的計算效果,并且改進后的算法克服了復(fù)數(shù)域矩陣計算這一問題,更加合理,應(yīng)用范圍更廣.