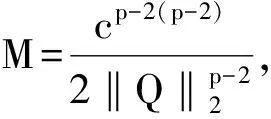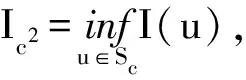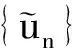袁志宏

(呂梁學院 數(shù)學系,山西 呂梁 033001)

0 引言

考慮下列Kirchhoff型問題

(1)

其中a,b>0為常數(shù),.

問題(1)中,當λ=0且|u|p-2u和RN分別用f(x,u)和有界區(qū)域Ω?R4代替時,轉化為基爾霍夫問題Dirichlet問題

這一問題最早可參考文獻[1]以及相關文獻.

近年來,國內外學者對Kirchhoff型方程進行了廣泛的研究并取得豐富的成果,其中對于問題(1),當p∈(2,2*)且λ是一個數(shù)或一個位勢函數(shù)時,已得到解的存在性結論;另外,當p∈(2,4)時,Li和Ye在文[2]中考慮了λ=-1的情形,并利用Nehari和Pohozaev不等式,得到在R3上至少有一個能量解的結論.最近文[3]討論了N≤3,P∈(2,2*)時,問題(1)的約束極小點的存在性.受此啟發(fā),這里討論N=4,P∈(2,3),問題(1)的可解性.

1 準備工作和主要結論

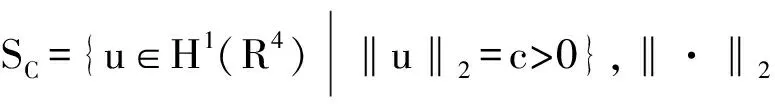
則問題(1)的約束基態(tài)解可轉化為求泛函I在Ic的臨界點,即對任意給定的c>0,若uc是I|Sc上的臨界點,λc為相應的Lagrange乘數(shù),則稱(uc,λc)為問題的解.

引理1[9](Gagliardo-Nirenberg不等式)若p∈(2,2*),N≥3,則

方便起見,我們記

則I(u)=A(u)+B(u)-C(u).且對任意的u∈Sc,由引理1可得

(2)

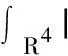
(3)

下面給出主要結論.

定理 若20.

2 主要結論的證明

引理2 若2

因20,則ut∈Sc,且當t→∞時

Ic2≤I(ut)=t2A(u)+t4B(u)-t2(p-2)C(u)→0.

即對任意的c>0,有Ic2<0.

2)設{un}?Sc為Ic2的極小化序列,則存在與n無關的正數(shù)k1,k2(k1

(4)

(5)

聯(lián)立(4)(5),Ic2

注 由上述定理可知,{c∈(0,+∞)|Ic2<0}≠?,不妨設c*=inf{c∈(0,+∞)|Ic2<0},顯然,c*=0.

引理3 若2

證明 因(I|Sc)′(u)=0,則存在λc∈R使得I′(u)-λcu=0,方程兩邊同時匹配u有

2A(u)+4B(u)-pC(u)=λcc2.

(6)

另一方面,根據(jù)Pohozaev不等式[6]

2A(u)+4B(u)-4C(u)=2λcc2,

(7)

下面給出定理的證明.

對20,設{un}?Sc為Ic2的極小化序列,由引理2知,Ic2<0且對任意的n∈N+,有

(8)

其中當n→+∞時°(1)→0.結合Brezis-Lieb引理,h:c→Ic2的連續(xù)性以及(8)有