NEW BOUNDS ON EIGENVUALUES OF LAPLACIAN?
Zhengchao JI(紀(jì)正超)
Center of Mathematical Scienses,Zhejiang University,Hangzhou 310027,China E-mail:jizhengchao@zju.edu.cn
Abstract In this paper,we investigate non-zero positive eigenvalues of the Laplacian with Dirichlet boundary condition in an n-dimentional Euclidean space Rn,then we obtain an new upper bound of the(k+1)-th eigenvalue λk+1,which improve the previous estimate which was obtained by Cheng and Yang,see(1.8).
Key words eigenvalues;Laplacian;Euclidean space;recursion formula
1 Introduction
The eigenvalue problem of Dirichlet Laplacian on a bounded domain ? with smooth boundary?? in an n-dimensional Euclidean space Rnis

where the△is the Laplacian in Rn.This problem has a real and purely discrete spectrum
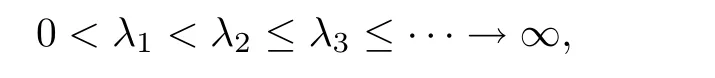
where each λihas finite multiplicity which is repeated according to its multiplicity.Recently,there are a lot of interesting results in this topic,see[1–5].
Because of the importance of the eigenvalue problem(1.1),many mathematicians focused on it and obtained a lot of great results.It is well known that Hilbert conjectured the research of the asymptotic behavior of the eigenvalue λkof the eigenvalue problem(1.1)would yield results of the utmost importance in the early part of twentieth century.In 1911,Weyl proved that
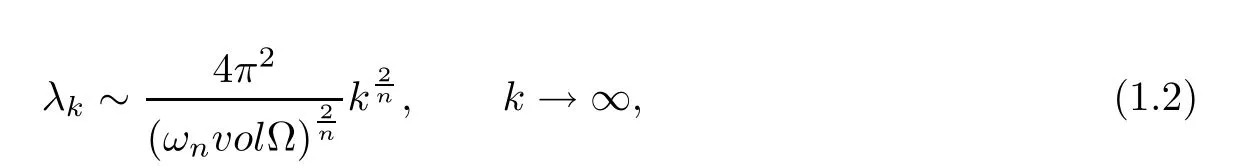
where ωnis the volume of the unit ball in Rn.Further,Pólya conjectured the eigenvalue λkshould satisfy

for k=1,2,···(see[5]).On the conjecture of Pólya,Li and Yau[5]attacked it and obtained

for k=1,2,···.
On the other side,Stewartson and Waechter[6]put forward an inverse question:let ψ be the set of all increasing sequences of positive numbers which tend to in finity,can one identify those sequence in ψ which correspond to spectra of the eigenvalue problem(1.1)for some domain?The research on the universal inequalities plays an important role to this problem.
When Mnis a bounded domain of an n-dimensional Euclidean space Rn,Payne,Pólya and Weinberger[6,7]obtained

By extending the universal inequality of Payne,Pólya and Weinberger in di ff erential background,there are two main contributions due to Hile and Protter[8]and Yang[9].In 1980,Hile and Protter proved

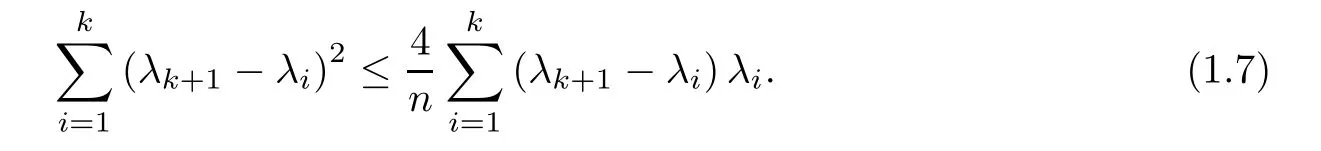
In 2007,by making use of a celebrated recursion formula,Cheng and Yang[10]obtained a sharp upper bound of the(k+1)-th eigenvalue

Furthermore,Yang[9]obtained a very sharp universal inequality
The purpose of this paper is to study the eigenvalues of the Dirichlet Laplacian.By introducing a new parameter we got a shaper recursion formula of Cheng and Yang[10].Here are our main results.
Theorem 1.1Let λ1≤ λ2≤ ···≤ λk+1be any positive real numbers satisfying
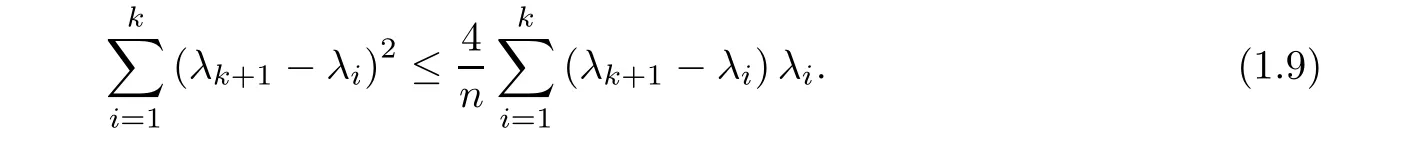
Then,we have
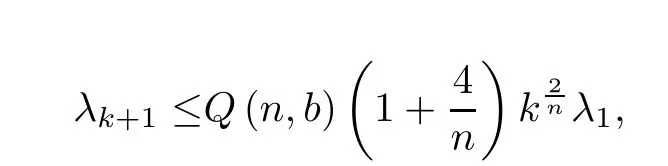
Corollary 1.2Let ??Rnbe a bounded domain with smooth boundary.Then the eigenvalues of Dirichlet Laplacian satisfy
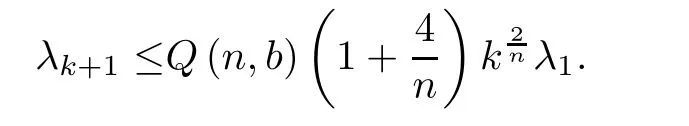
Remark 1.3When b=1,this upper bound is the same as(1.8).
2 Some Recursion Formulas
In this section,we shall prove some new recursion formulas,and use them to proof our main theorem.First let’s give this lemma,which will be used later.
Lemma 2.1For any n≥1,k≥1 andwe have
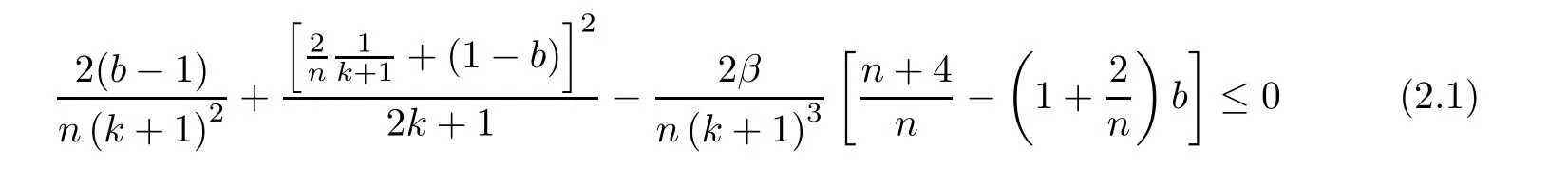
provided
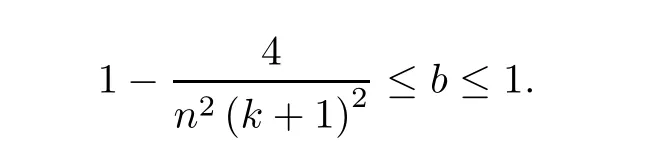
ProofPut
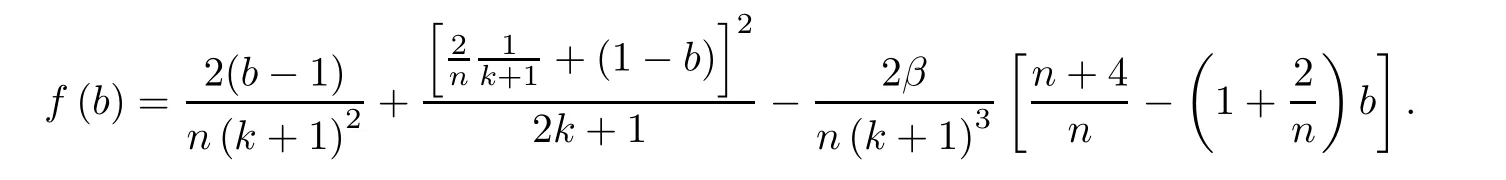
It’s easy to check that f(1)=0.We rewrite f(b)as

where F is a constant independent of b.Since n≥1,k≥1,we have
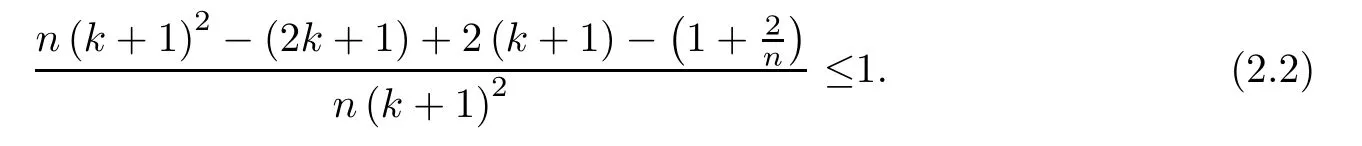
Thus when b≤1 and the coefficients of b2and b satisfy
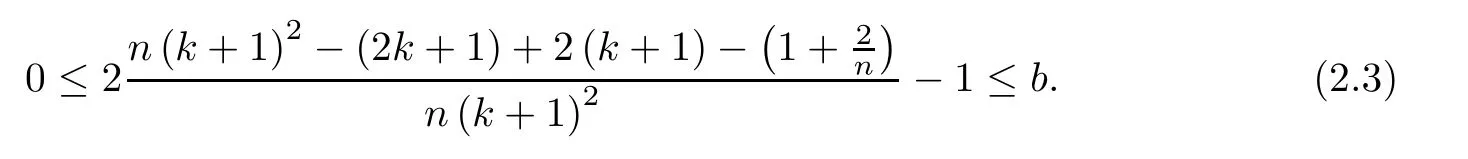
we have f(b)≤0.And(2.3)is equal to
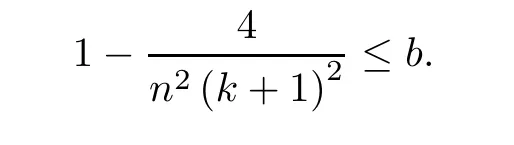
Now we prove our recursion formula which is the key to prove our main theorem.
Theorem 2.2Let λ1≤ λ2≤ ···≤ λk+1be any positive real numbers satisfying(1.9).For b>0,de fine
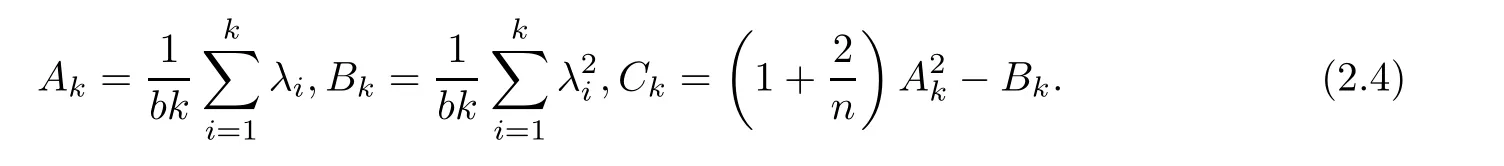
If

then
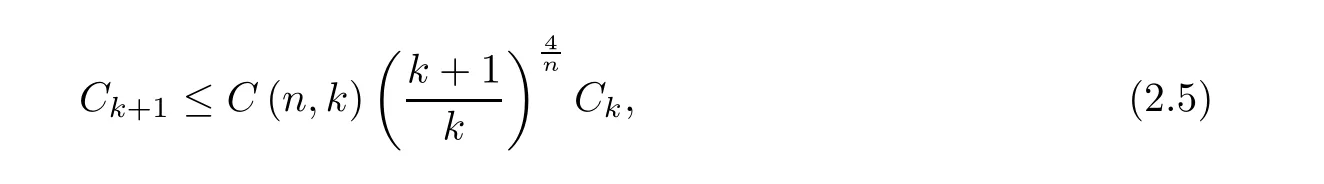
where
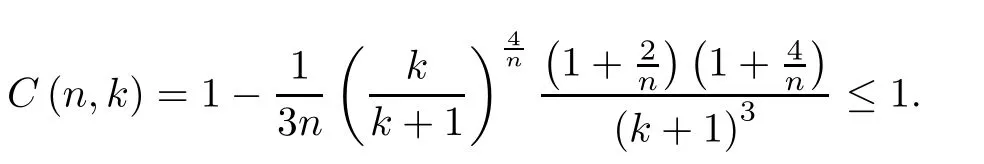
ProofPut
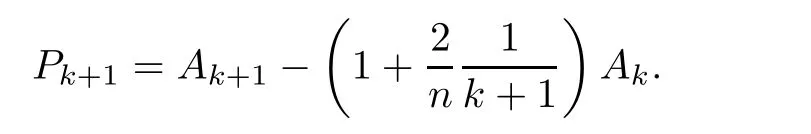
Since
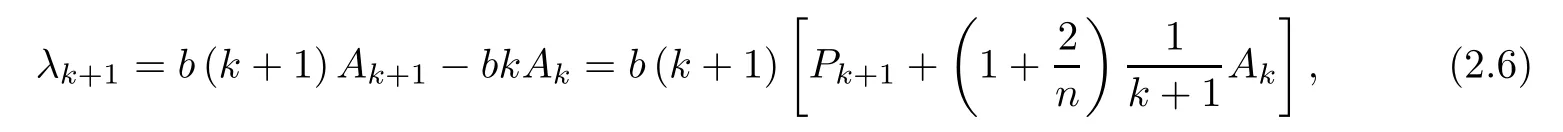
we have
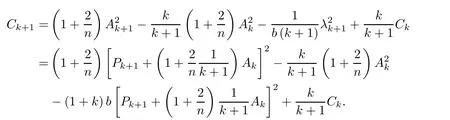
Hence we get
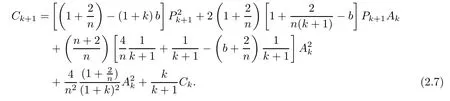
From(1.7)and(2.4),we have
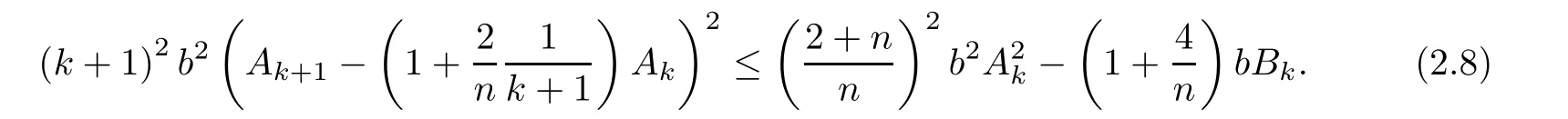
By the de finition of Pk+1,(2.4)and(2.8),one infer

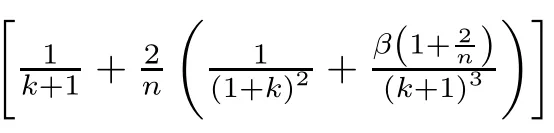
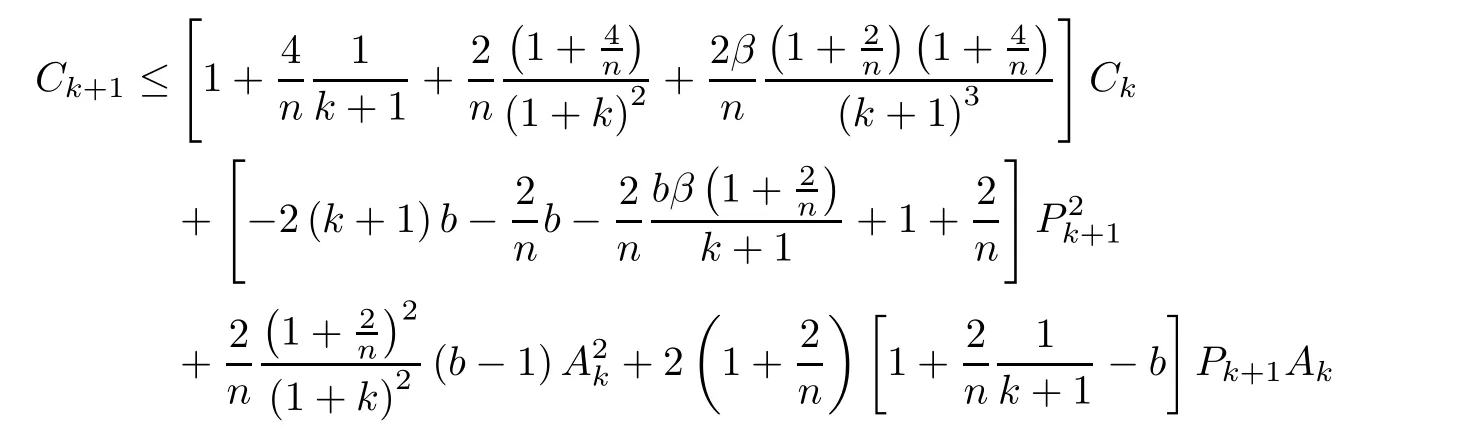
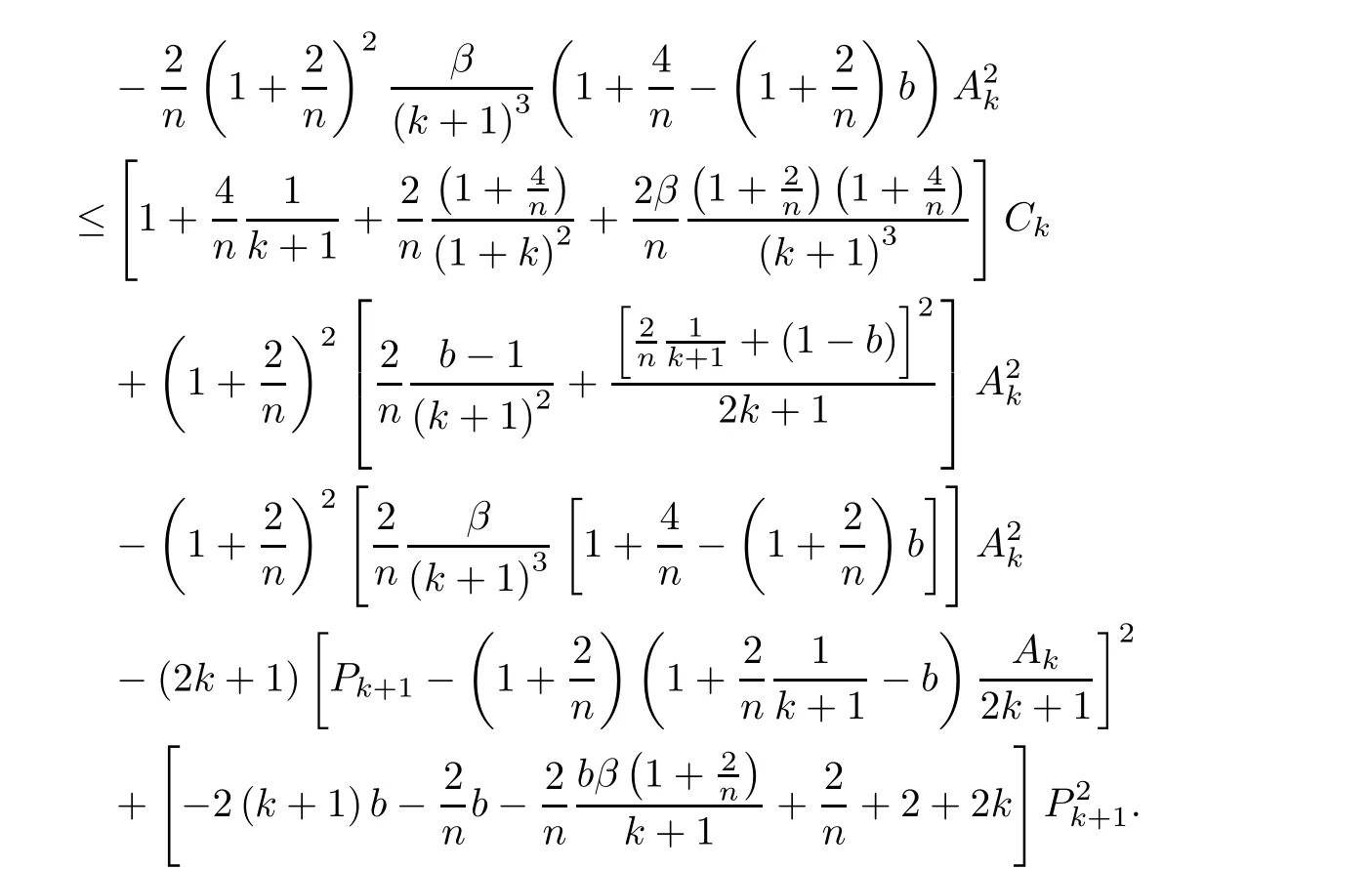
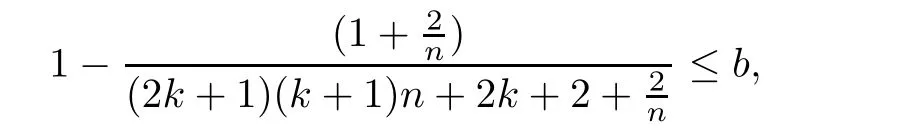
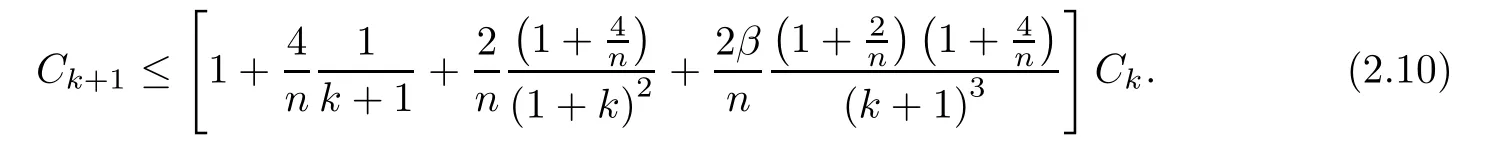
Since
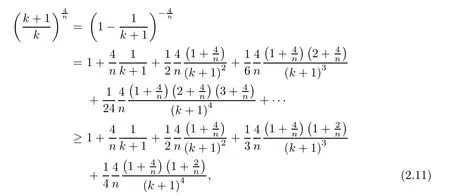
we get our general recursion formula,
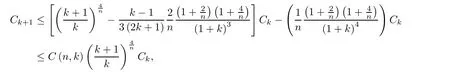
where
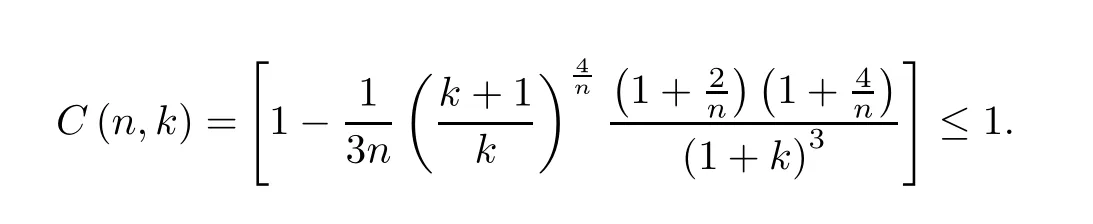
Now we give the proof of our main result by the given recursion formula.
By making use of formula(2.5)in Theorem 2.2,we have
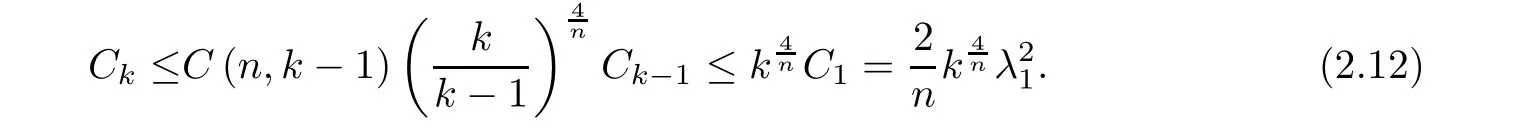
From(1.7),we have
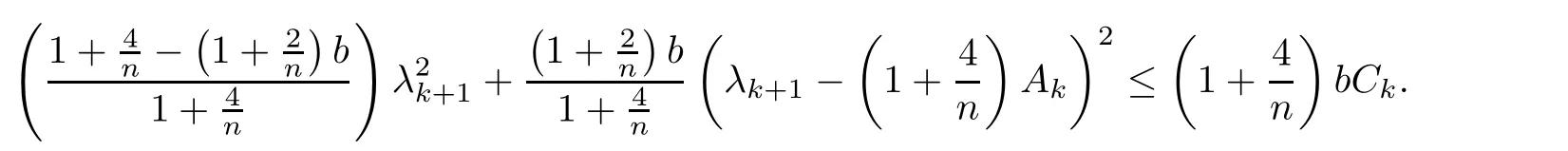
Thus we drive
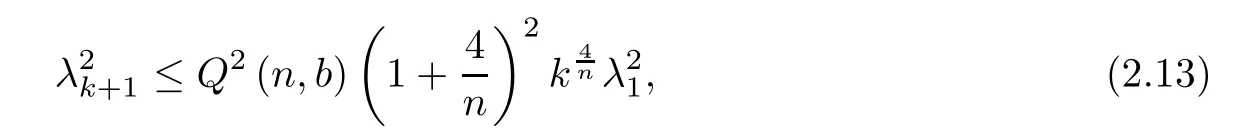
which completes the proof of Theorem 1.1.
AcknowledgementsThe author would like to thank Professor Kefeng Liu and Professor Hongwei Xu for their continued support,advice and encouragement.Thanks also to Professor En-Tao Zhao for helpful discussions.
 Acta Mathematica Scientia(English Series)2019年2期
Acta Mathematica Scientia(English Series)2019年2期
- Acta Mathematica Scientia(English Series)的其它文章
- NUMERICAL ANALYSIS FOR VOLTERRA INTEGRAL EQUATION WITH TWO KINDS OF DELAY?
- LARGE TIME BEHAVIOR OF SOLUTION TO NONLINEAR DIRAC EQUATION IN 1+1 DIMENSIONS?
- A NONTRIVIAL SOLUTION OF A QUASILINEAR ELLIPTIC EQUATION VIA DUAL APPROACH?
- BLOW-UP PHENOMENA FOR A CLASS OF GENERALIZED DOUBLE DISPERSION EQUATIONS?
- APPROXIMATE SOLUTION OF P-RADICAL FUNCTIONAL EQUATION IN 2-BANACH SPACES?
- VECTORIAL EKELAND VARIATIONAL PRINCIPLE AND CYCLICALLY ANTIMONOTONE EQUILIBRIUM PROBLEMS?
