APPROXIMATE SOLUTION OF P-RADICAL FUNCTIONAL EQUATION IN 2-BANACH SPACES?
Muaadh ALMAHALEBI
Department of Mathematics,Faculty of Sciences,University of Ibn Tofail,Kenitra,Morocco E-mail:muaadh1979@hotmail.fr Abdellatif CHAHBI
Department of Mathematics,Faculty of Sciences,University of Ibn Zohr,Agadir,Morocco E-mail:ab 1980@live.fr
Abstract The aim of this paper is to introduce and solve the p-radical functional equation
Key words stability;hyperstability;2-Banach spaces;p-radical functional equations
1 Introduction
Throughout this paper,we will denote the set of natural numbers by N,the set of real numbers by R and R+=[0,∞)the set of nonnegative real numbers.By Nm,m∈N,we will denote the set of all natural numbers greater than or equal to m.
The notion of linear 2-normed spaces was introduced by G?hler[23,24]in the middle of 1960s.We need to recall some basic facts concerning 2-normed spaces and some preliminary results.
De finition 1.1Let X be a real linear space with dimX>1 and k·,·k:X ×X ?→ [0,∞)be a function satisfying the following properties:
(1)kx,yk=0 if and only if x and y are linearly dependent,(2)kx,yk=ky,xk,
(3)kλx,yk=|λ|kx,yk,
(4)kx,y+zk≤kx,yk+kx,zk
for all x,y,z ∈ X and λ ∈ R.Then the function k·,·k is called a 2-norm on X and the pair(X,k·,·k)is called a linear 2-normed space.Sometimes condition(4)called the triangle inequality.
Example 1.2For x=(x1,x2),y=(y1,y2)∈X=R2,the Euclidean 2-norm kx,ykR2is de fined by
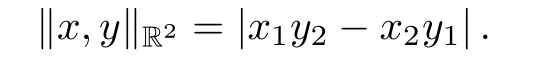
Lemma 1.3Let(X,k·,·k)be a 2-normed space.If x ∈ X and kx,yk=0 for all y ∈ X,then x=0.
De finition 1.4A sequence{xk}in a 2-normed space X is called a convergent sequence if there is an x∈X such that
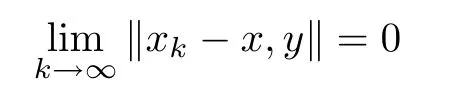
for all y∈X.If{xk}converges to x,write xk?→x with k?→∞ and call x the limit of{xk}.In this case,we also write
De finition 1.5A sequence{xk}in a 2-normed space X is said to be a Cauchy sequence with respect to the 2-norm if
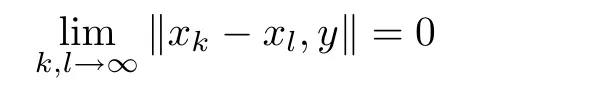
for all y∈X.If every Cauchy sequence in X converges to some x∈X,then X is said to be complete with respect to the 2-norm.Any complete 2-normed space is said to be a 2-Banach space.
Now,we state the following results as lemma(see[28]for the details).
Lemma 1.6Let X be a 2-normed space.Then,
(2)if kx,zk=0 for all z∈X,then x=0,
(3)for a convergent sequence xnin X,
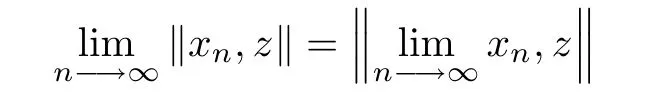
for all z∈X.
The concept of stability for a functional equation arises when de fining,in some way,the class of approximate solutions of the given functional equation,one can ask whether each mapping from this class can be somehow approximated by an exact solution of the considered equation.Namely,when one replaces a functional equation by an inequality which acts as a perturbation of the considered equation.The first stability problem of functional equation was raised by Ulam[32]in 1940.This included the following question concerning the stability of group homomorphisms.
Let(G1,?1)be a group and let(G2,?2)be a metric group with a metric d(·,·).Given ε >0,does there exist a δ>0 such that if a mapping h:G1→ G2satis fies the inequality
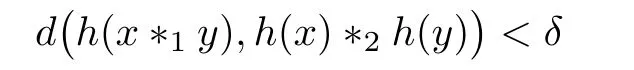
for all x,y∈G1,then there exists a homomorphism H:G1→G2with

for all x∈G1?
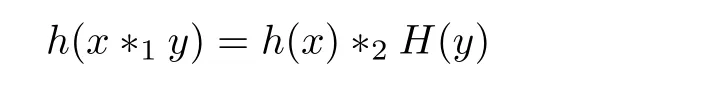
If the answer is affirmative,we say that the equation of homomorphism is stable.Since then,this question attracted the attention of many researchers.In 1941,Hyers[25]gave a first partial answer to Ulam’s question and introduced the stability result as follows:
Theorem 1.7(see[25]) Let E1and E2be two Banach spaces and f:E1→E2be a function such that
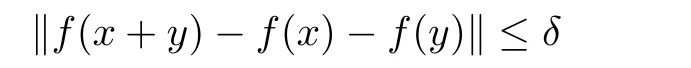
for some δ>0 and for all x,y ∈ E1.Then the limit
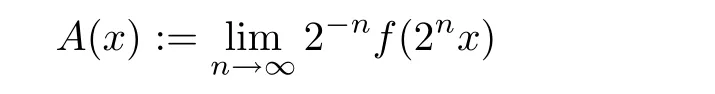
exists for each x∈E1,and A:E1→E2is the unique additive function such that
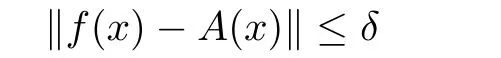
for all x∈E1.Moreover,if f(tx)is continuous in t for each fixed x∈E1,then the function A is linear.
Later,Aoki[9]and Bourgin[10]considered the problem of stability with unbounded Cauchy di ff erences.Rassias[29]attempted to weaken the condition for the bound of the norm of Cauchy di ff erence
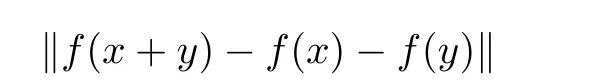
and proved a generalization of Theorem 1.7 using a direct method(cf.Theorem 1.8).
Theorem 1.8(see[29]) Let E1and E2be two Banach spaces.If f:E1→E2satis fies the inequality
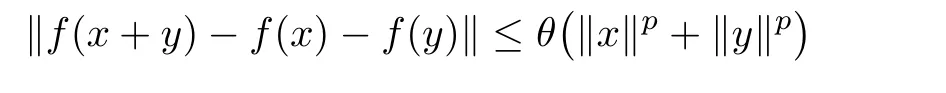
for some θ≥0 for some p∈R with 0≤p<1,and for all x,y∈E1,then there exists a unique additive function A:E1→E2such that
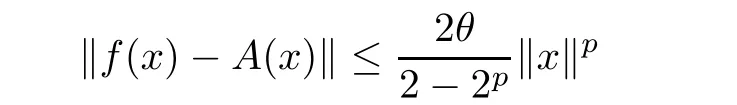
for each x∈E1.If,in addition,f(tx)is continuous in t for each fixed x∈E1,then the function A is linear.
After then,Rassias[30,31]motivated Theorem 1.8 as follows.
Theorem 1.9(see[30,31]) Let E1be a normed space,E2be a Banach space,and f:E1→E2be a function.If f satis fies the inequality
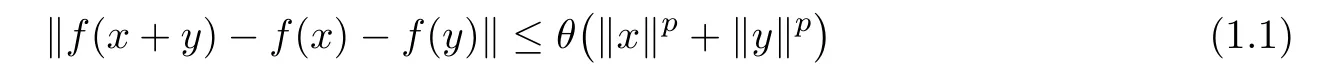
for some θ≥ 0,for some p∈ R withand for all x,y∈ E1?{0E1},then there exists a unique additive function A:E1→E2such that
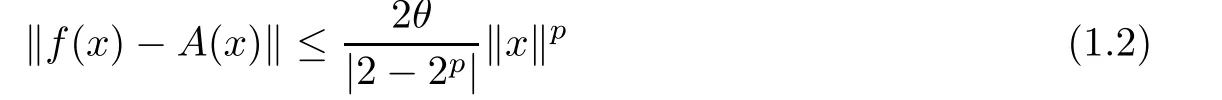
for each x∈E1?{0E1}.
Note that Theorem 1.9 reduces to Theorem 1.7 when p=0.For p=1,the analogous result is not valid.Also,Brzdk[11]showed that estimation(1.2)is optimal for p ≥ 0 in the general case.
Theorem 1.10(see[13]) Let X be a nonempty set,(Y,d)be a complete metric space,andbe a non-decreasing operator satisfying the hypothesis
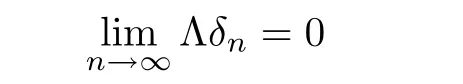
for every sequence{δn}n∈Nin YXwith
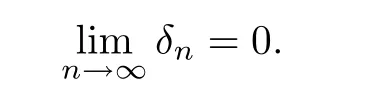
Suppose that T:YX→YXis an operator satisfying the inequality
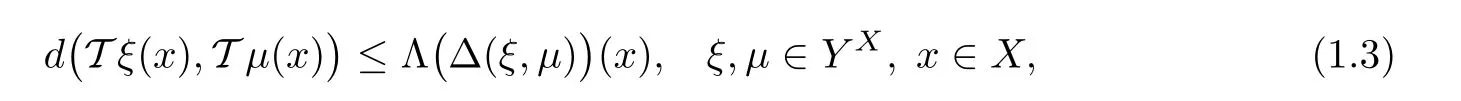
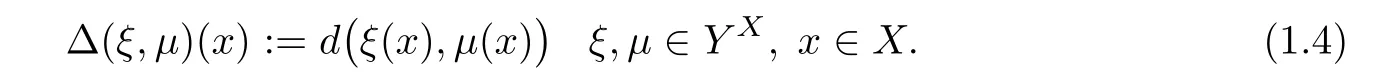

and
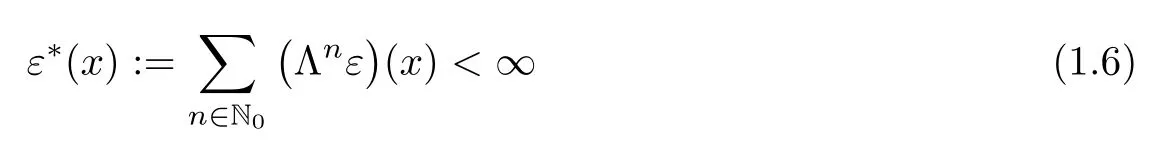
for all x∈X,then the limit

exists for each x ∈X.Moreover,the function ψ ∈ YXde fined by

is a fixed point of T with

for all x∈X.
Theorem 1.11(see[14]) Let X be a nonempty set,(Y,d)be a complete metric space,f1,···,fr:X → X and L1,···,Lr:X → R+be given mappings.Suppose that T:YX→ YXandare two operators satisfying the conditions
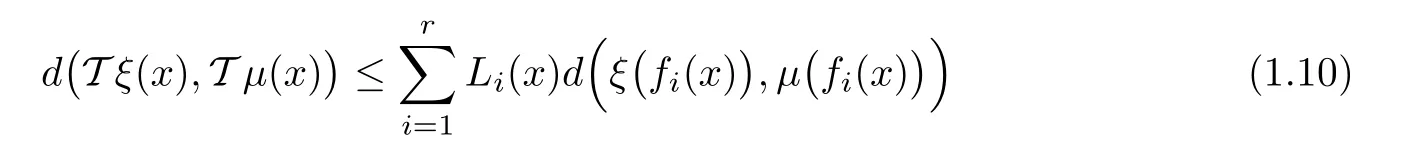
for all ξ,μ ∈ YX,x ∈ X and
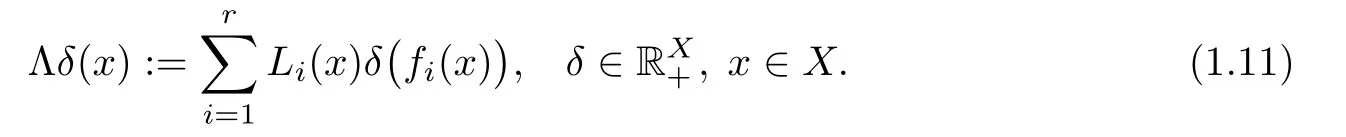
If there exist functions ε:X → R+and ? :X → Y such that

and
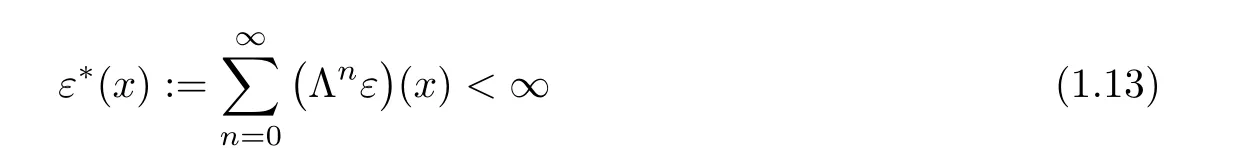
for all x∈X,then the limit(1.7)exists for each x∈X.Moreover,the function(1.8)is a fixed point of T with(1.9)for all x∈X.
Then by using this theorem,Brzdk[14]improved,extended and complemented several earlier classical stability results concerning the additive Cauchy equation(in particular Theorem 1.9).Over the last few years,many mathematicians have investigated various generalizations,extensions and applications of the Hyers-Ulam stability of a number of functional equations(see,for instance,[1–5,16,17]and references therein);in particular,the stability problem of the radical functional equations in various spaces was proved in[6–8,21,22,26,27].
Now,we state an analogue of Theorem 1.11 in 2-Banachspaces.Another version of Theorem 1.11 in 2-Banach space can be found in[20].
Theorem 1.12Let X be a nonempty set,?Y,k·,·k?be a 2-Banach space,g:X → Y be a surjective mapping and let f1,···,fr:X → X and L1,···,Lr:X → R+be given mappings.Suppose thatandare two operators satisfying the conditions
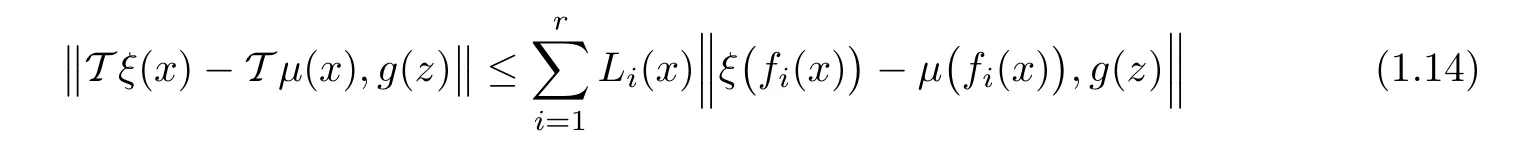
for all ξ,μ ∈ YX,x,z ∈ X and

If there exist functions ε:X ×X → R+and ? :X → Y such that
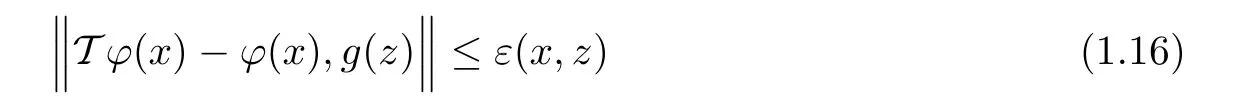
and
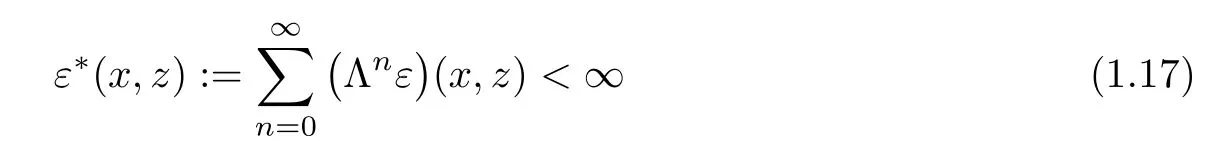
for all x,z∈X,then the limit

exists for each x∈X.Moreover,the function ψ:X→Y de fined by

is a fixed point of T with
for all x,z∈X.
ProofFirst,we use the mathematical induction to show that,for every n∈N0,
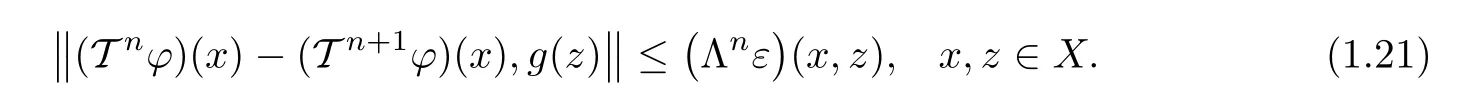
Clearly,by(1.16),the case n=0 is trivial.Now,for n∈N1,suppose that(1.21).Then,using(1.14)and inductive assumption,for every x,z∈X,we obtain

completing the proof of(1.21).Therefore,for n,k∈N0,k>0,
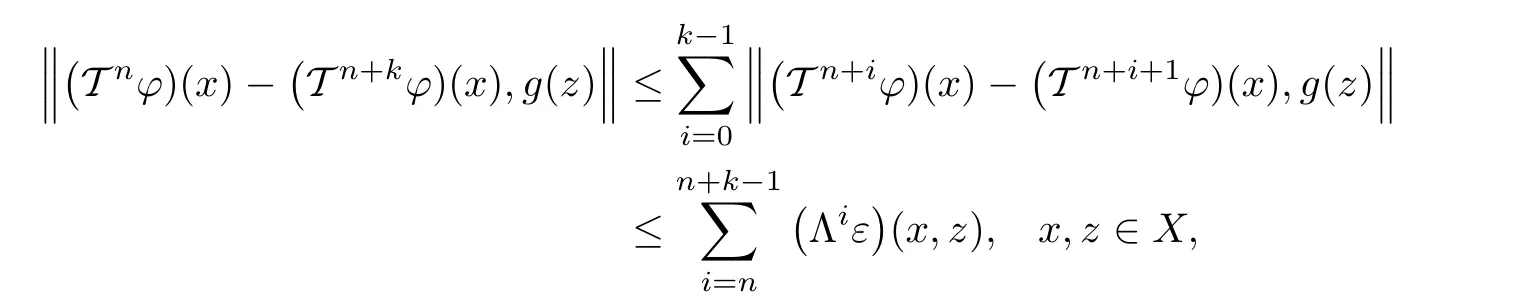
then
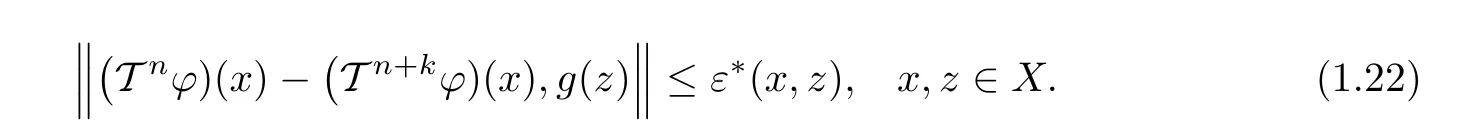
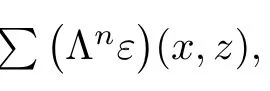
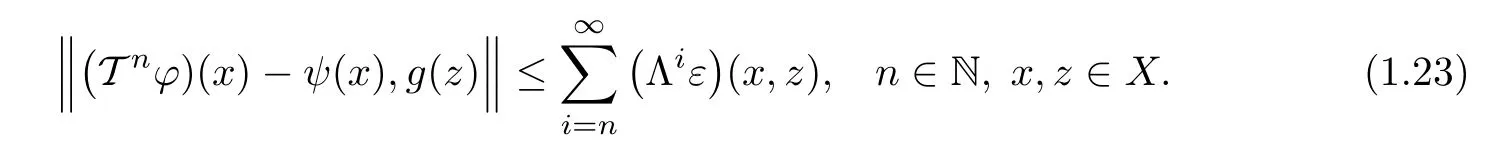
Putting n=0 in(1.23),we obtain that(1.20)holds for all x,z∈X.In view of(1.14),we conclude
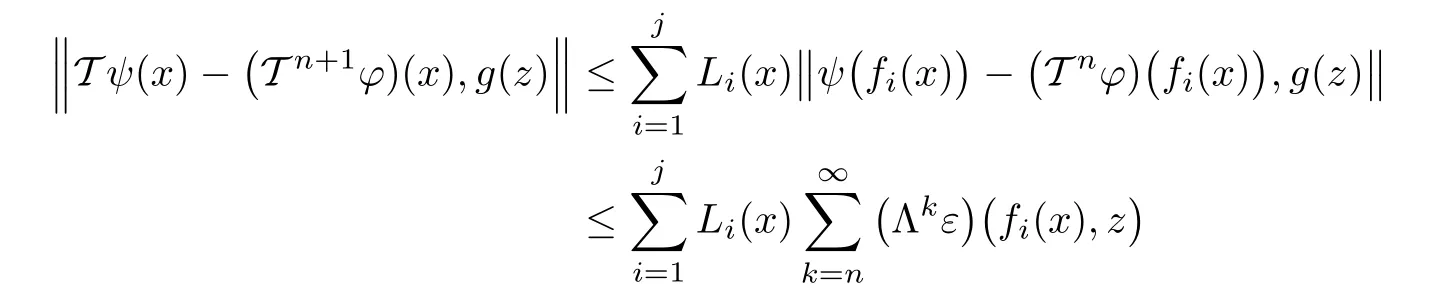
for all n∈N0and all x,z∈X.Letting n→∞ in in the last inequality,we get T(ψ)=ψ.For the uniqueness of ψ,suppose that ψ1,ψ2∈ YXare two fixed points of T such that
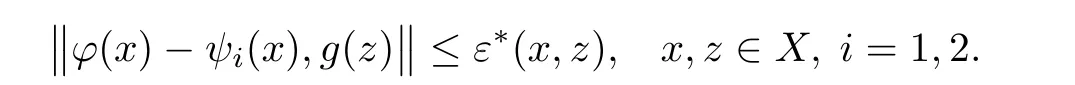
For every m∈N0,we show that
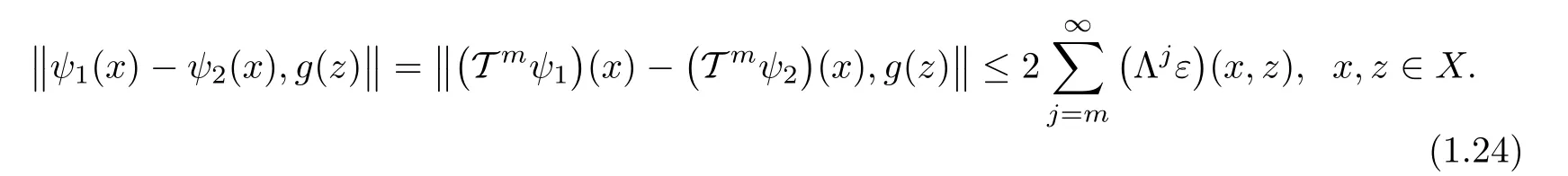
For the case m=0,we have
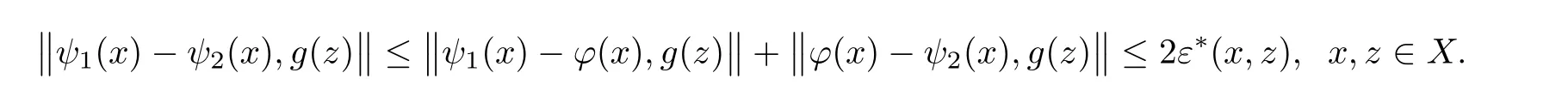
Next,we assume that(1.24)is valid for some m∈N1.Then,by using(1.14),for every x,z∈X,we get the following inequality
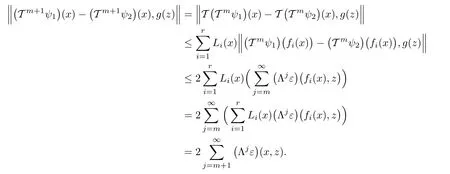
Therefore,we prove that(1.24)holds for any m∈N0.Now,letting m→∞,on account of(1.17),we get ψ1= ψ2.
In 2016,Aiemsomboon and Sintunavarat[7]used Theorem 1.11 to investigate a new type of stability for the radical quadratic functional equation of the form
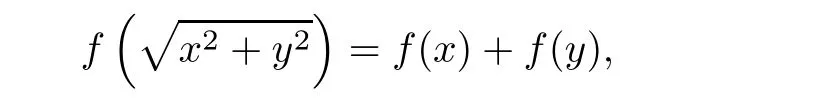
where f is a self-mapping on the set of real numbers and they generalized some earlier classical results concerning the Hyers-Ulam stability for that functional equations.
In this paper,we achieve the general solutions of the following p-radical functional equation:

and discuss the generalized Hyers-Ulam-Rassias stability problem in 2-Banach spaces by using Theorem 1.12.
2 Solution of Equation(1.25)
In this section,we give the general solution of functional equation(1.25).The next theorem can be derived from([19],Corollary 2.3 and Proposition 2.4(a)).However,for the convenience of readers we present it with a direct proof.
Theorem 2.1Let Y be a linear space.A function f:R→Y satis fies the functional equation(1.25)if and only if

with some additive function F:R→Y.
ProofIndeed,It is not hard to check without any problem that if f:R→Y satis fies(2.1),then it is a solution to(1.25).On the other hand,if f:R→Y is a solution of(1.25),then we consider the following two cases.
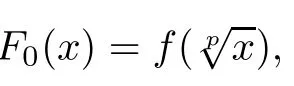
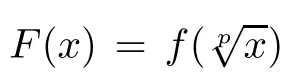
3 Approximation of the p-Radical Functional Equation(1.25)
In the following two theorems,we use Theorem 1.12 to investigate the generalized Hyers-Ulam stability of the p-radical functional equation(1.25)in 2-Banach spaces.
Hereafter,we assume that?Y,k·,·k?is a 2-Banach space.
Theorem 3.1Let h1,h2:R2→R+be two functions such that
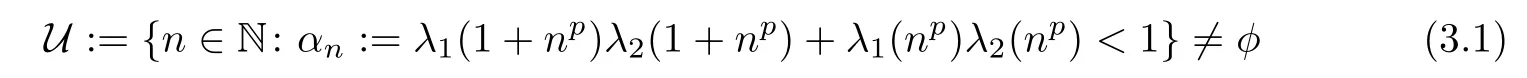
is an in finite set,where
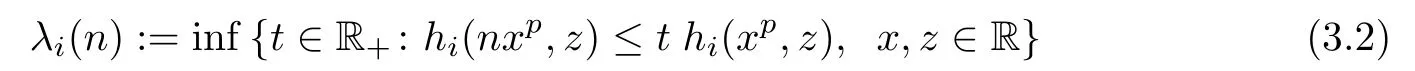
for all n∈N,where i=1,2.Assume that f:R→Y satis fies the inequality
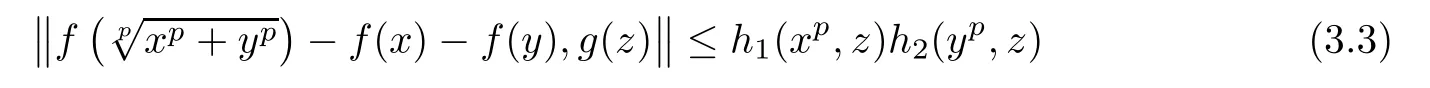
for all x,y,z∈R.Then there exists a unique p-radical function F:R→Y such that
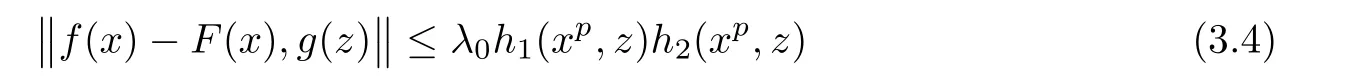
for all x,z∈R,where
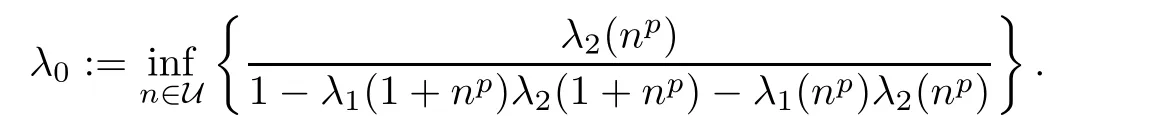
ProofReplacing y with mx,where x∈R and m∈N,in inequality(3.3),we get
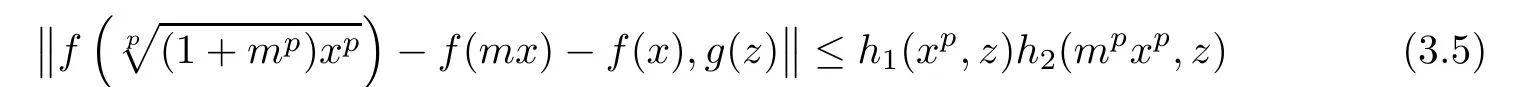
for all x,z∈R.For each m∈N,we de fine the operator Tm:YR→YRby
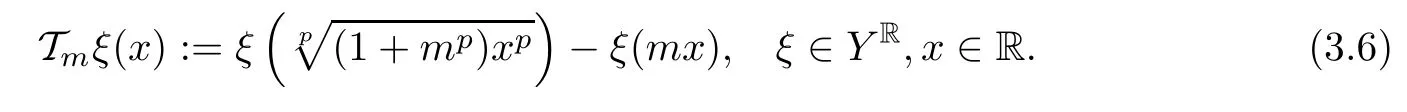
Further put
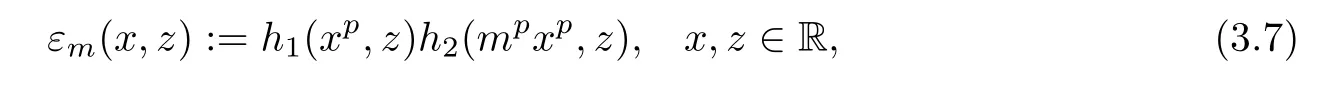
and observe that
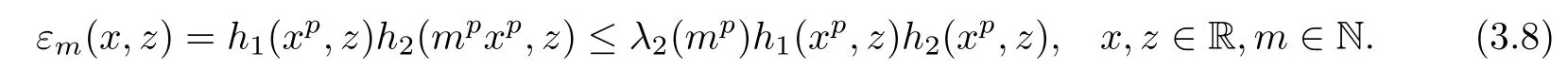
Then inequality(3.5)takes the form
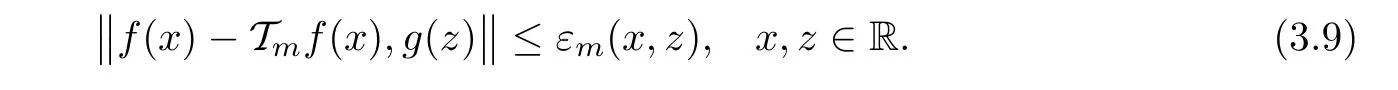
Furthermore,for every x,z ∈ R,ξ,μ ∈ YR,we obtain
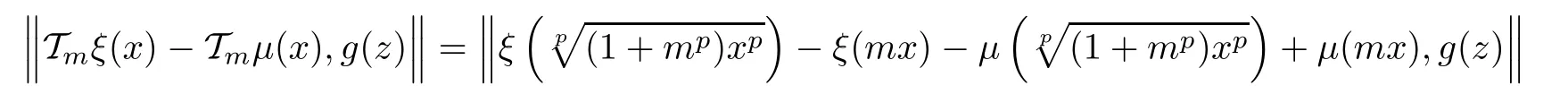
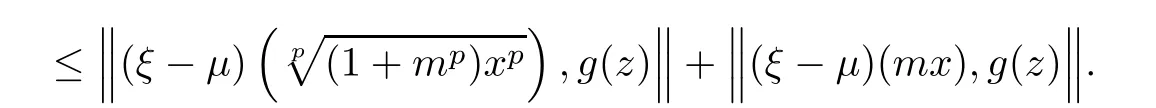
This brings us to de fine the operatorby

For each m∈N,the above operator has the form described in(1.15)withf2(x)=mx and L1(x)=L2(x)=1 for all x∈R.By induction,we will show that for each x,z∈R,n∈N0,and m∈U we have
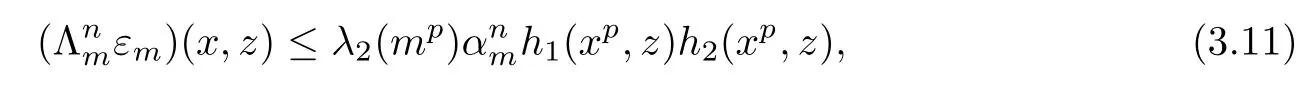
where
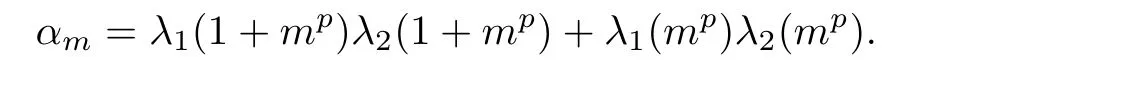
From(3.7)and(3.8),we obtain that inequality(3.11)holds for n=0.Next,we will assume that(3.11)holds for n=k,where k∈N.Then we have
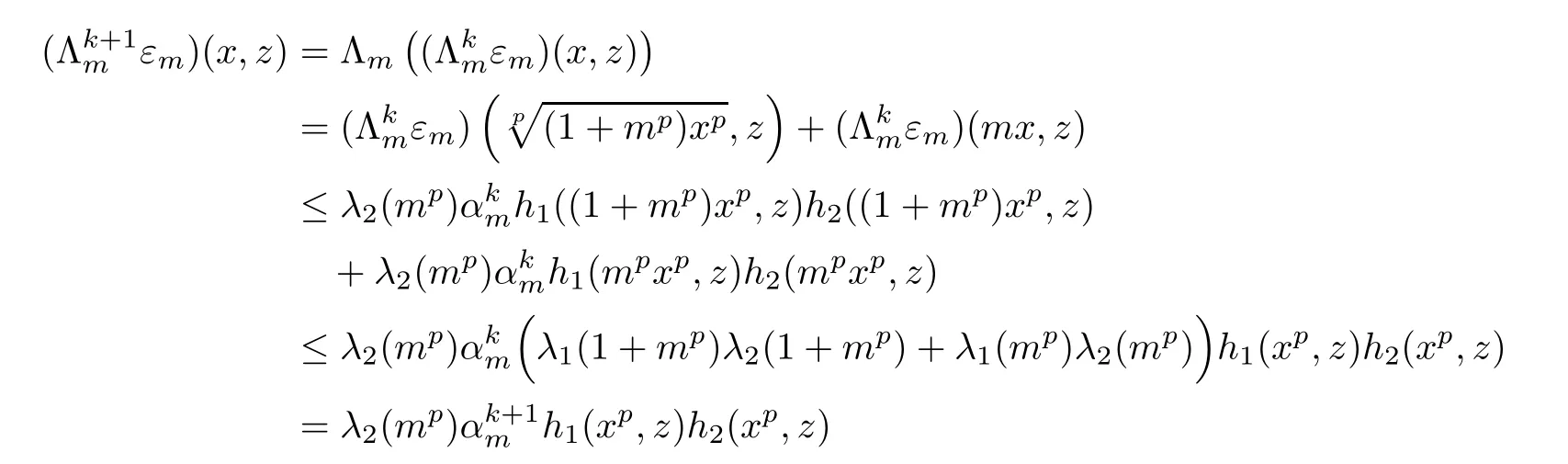
for all x,z∈R,m∈U.This shows that(3.11)holds for n=k+1.Now we can conclude that inequality(3.11)holds for all n∈N0.Hence,we obtain
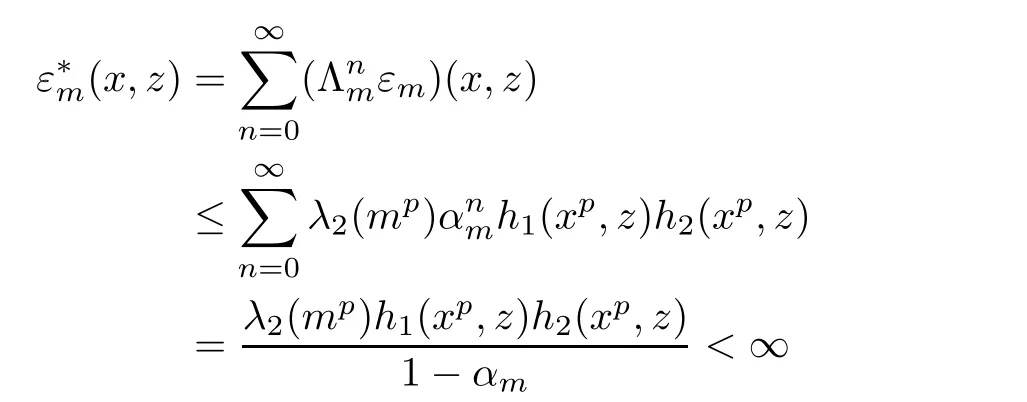
for all x,z∈R,m ∈U.Therefore,according to Theorem 1.12 with ?=f and X=R and using the surjectivity of g,we get that the limit
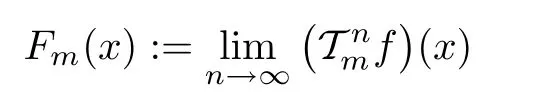
exists for each x∈R and m∈U,and
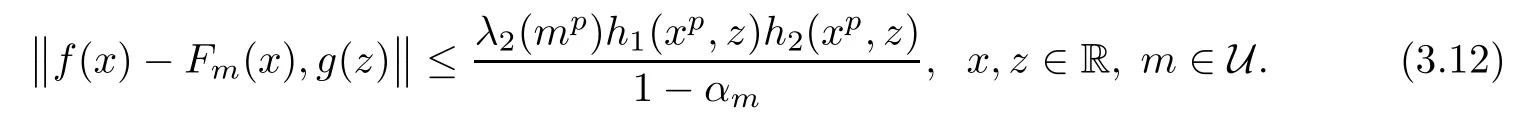
To prove that Fmsatis fies the functional equation(1.25),just prove the following inequality
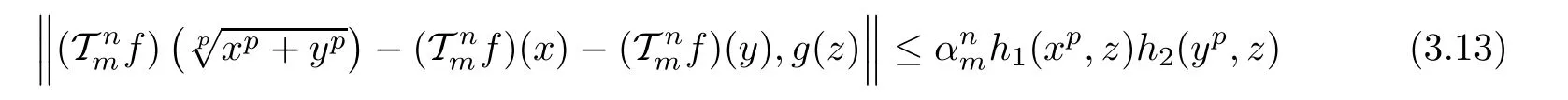
for every x,y,z∈R,n∈N0,and m∈U.Since the case n=0 is just(3.3),take k∈N and assume that(3.13)holds for n=k and every x,y,z∈R,m∈U.Then,for each x,y,z∈R and m∈U,we get

Thus,by induction,we show that(3.13)holds for every x,y,z∈R,n∈N0,and m∈U.Letting n→∞in(3.13),we obtain the equality
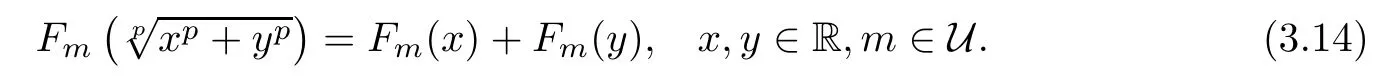
This implies that Fm:R→Y,de fined in this way,is a solution of the equation
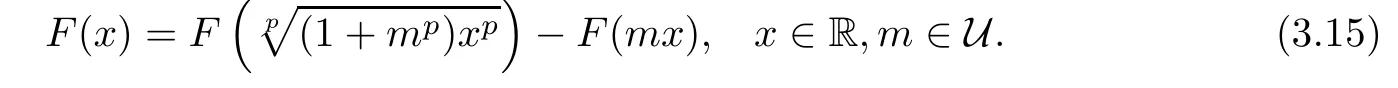
Next,we will prove that each p-radical function F:R→Y satisfying the inequality
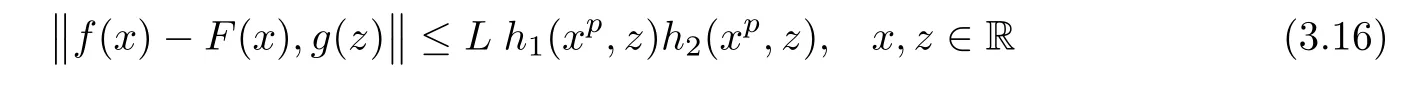
with some L>0,is equal to Fmfor each m∈U.To this end,we fix m0∈U and F:R→Y satisfying(3.16).From(3.12),for each x,z∈R,we get
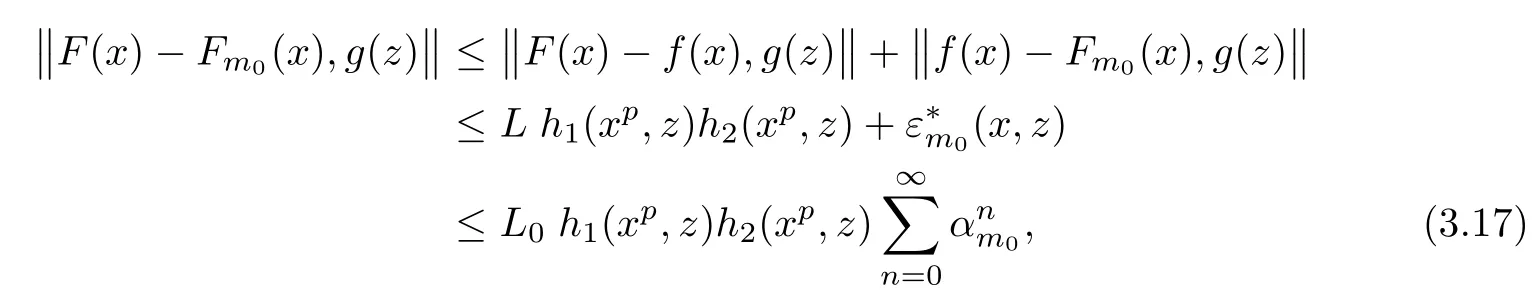
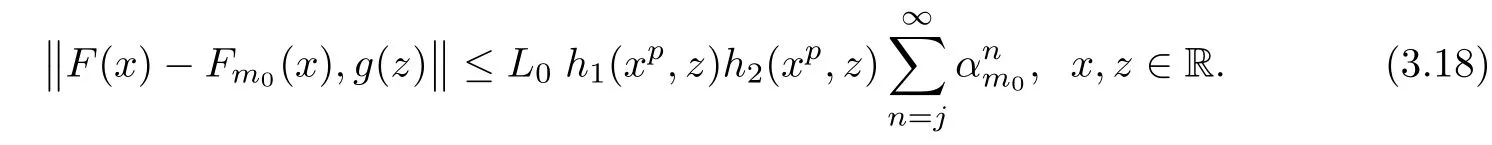
The case j=0 is exactly(3.17).We fix k∈N and assume that(3.18)holds for j=k.Then,in view of(3.17),for each x,z∈R,we get


This shows that(3.18)holds for j=k+1.Now we can conclude that inequality(3.18)holds for all j∈N0.Now,letting j→∞in(3.18),we get

Thus,we have also proved that Fm=Fm0for each m∈U,which(in view of(3.12))yields
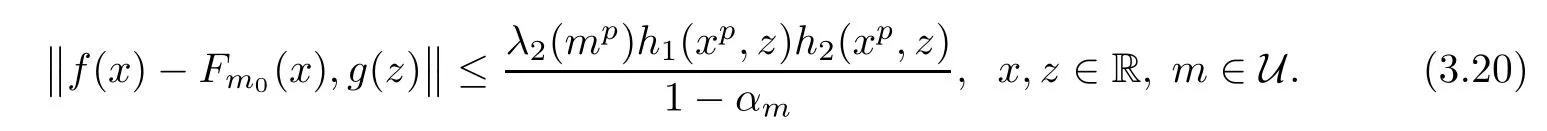
This implies(3.4)with F=Fm0and(3.19)con firms the uniqueness of F.
By a similar way we can prove the following theorem.
Theorem 3.2Let h:R2→R+be a function such that

is an in finite set,where
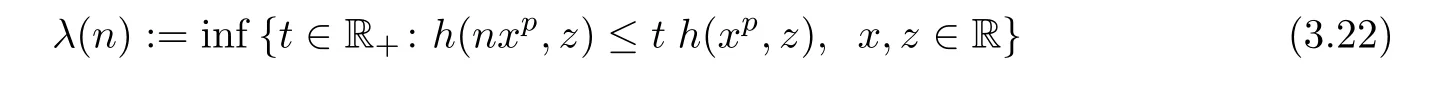
for all n∈N.Assume that f:R→Y satis fies the inequality
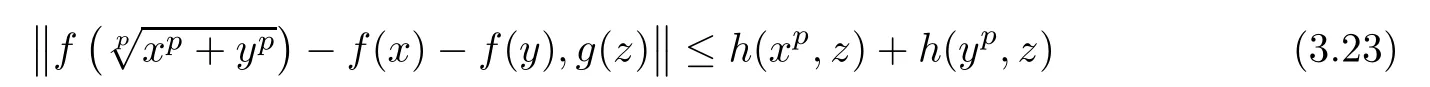
for all x,y,z∈R.Then there exists a unique p-radical function F:R→Y such that
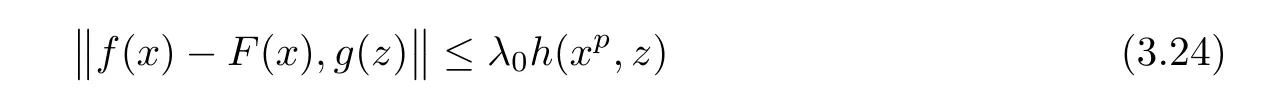
for all x,z∈R,where
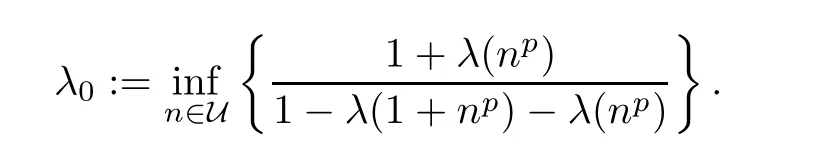
ProofReplacing in(3.23)y by mx,where x∈R and m∈N,we get
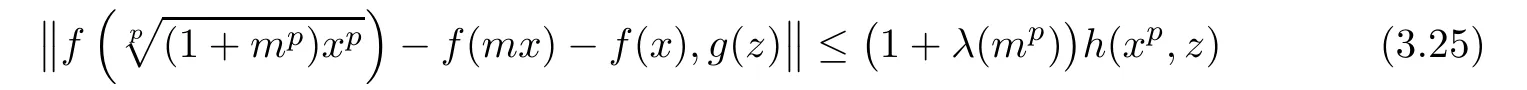
for all x,z∈R.For each m∈N,we de fine
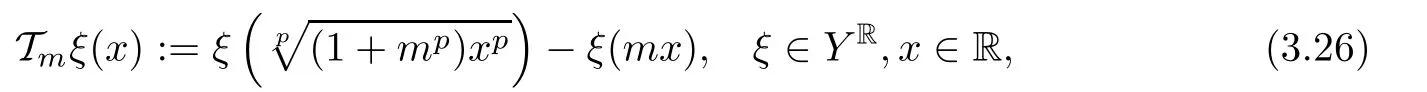
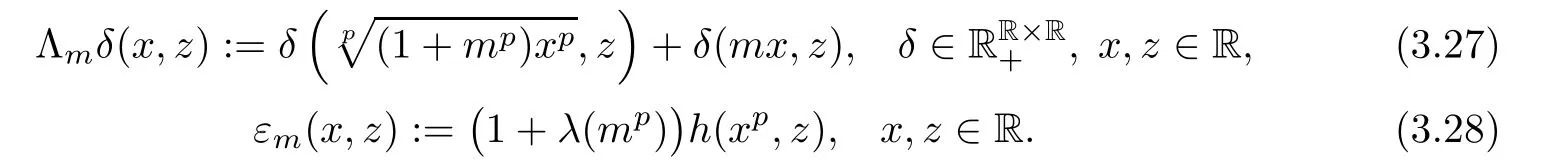
As in Theorem 3.1,we observe that(3.25)takes form
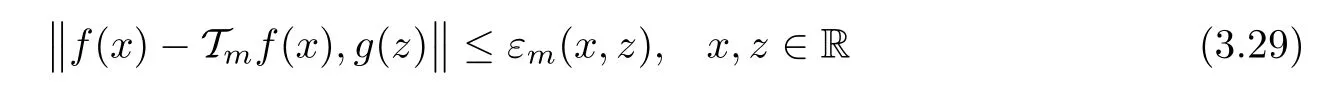
Λmhas the form described in(1.15)and(1.14)is valid for every ξ,μ ∈ YR,x,z ∈ R.It is not hard to show that
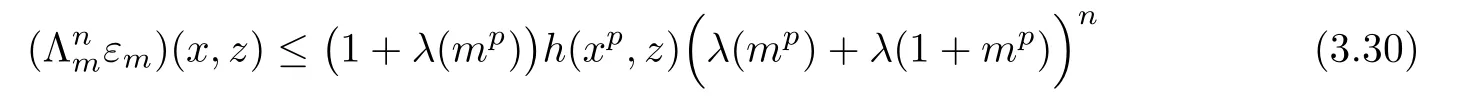
for all x,z∈R and n∈N0.Therefore
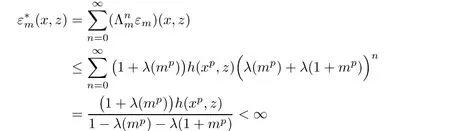
for all x,z∈R and m∈U.Also the remaining reasonings are analogous as in the proof of Theorem 3.1. ?
The following theorem concerns the η-hyperstability of(1.25)in 2-Banach spaces.Namely,We consider functions f:R→Y ful filling(1.25)approximately,i.e.,satisfying the inequality
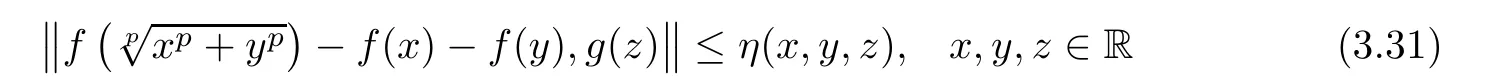
with η:R3→R+is a given mapping.Then we find a unique p-radical function F:R→Y which is close to f.Then,under some additional assumptions on η,we prove that the conditional functional equation(1.25)is η-hyperstable in the class of functions f:R → Y,i.e.,each f:R → Y satisfying inequality(3.31),with such η,must ful fil equation(1.25).
Theorem 3.3Let h1,h2and U be as in Theorem 3.1.Assume that
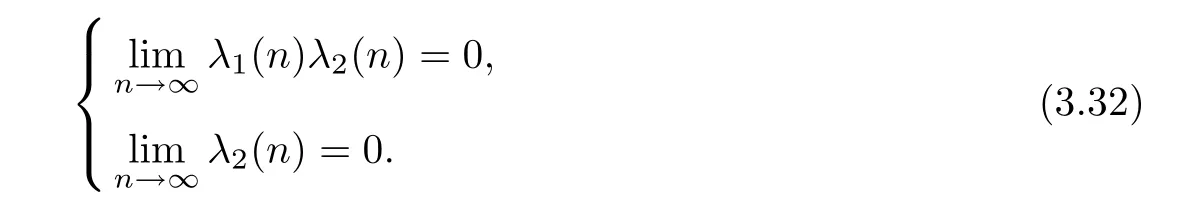
Then every f:R→Y satisfying(3.3)is a solution of(1.25).
ProofSuppose that f:R→Y satis fies(3.3).Then,by Theorem 3.1,there exists a mapping F:R→Y satis fies(1.25)and
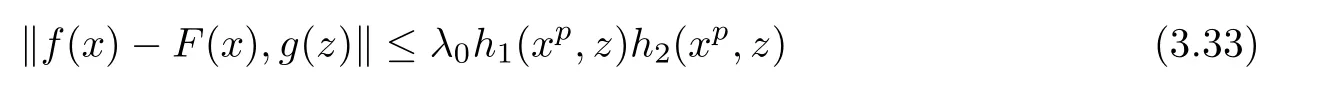
for all x,z∈R,where
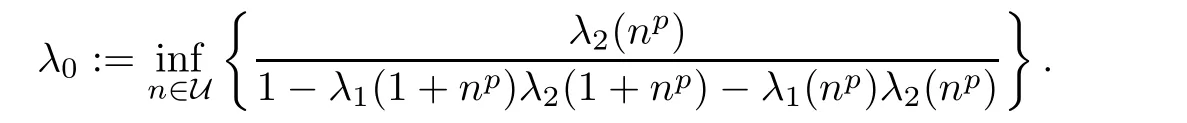
Since,in view of(3.32),λ0=0.This means that f(x)=F(x)for all x∈R,whence
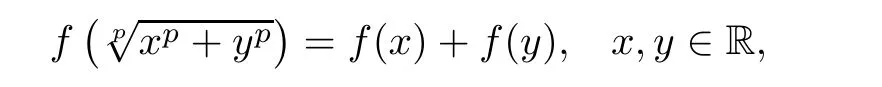
which implies that f satis fies the functional equation(1.25)on R.
4 Some Particular Cases
According to above theorems,we derive some particular cases from our main results.
Corollary 4.1Let h1,h2:R2→ (0,∞)be as in Theorem 3.1 such that

Assume that f:R→Y satis fies(1.25).Then there exist a unique p-radical function F:R→Y and a unique constant κ∈R+with
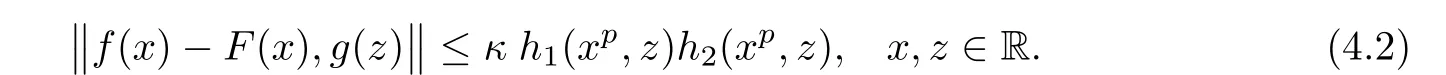
ProofBy the de finition of λi(n)in Theorem 3.1,we observe that

and
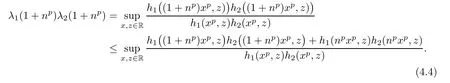
Combining inequalities(4.3)and(4.5),we get
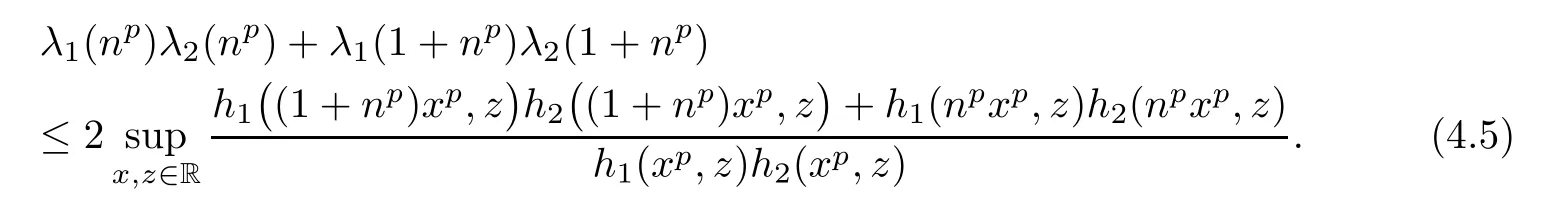
Write
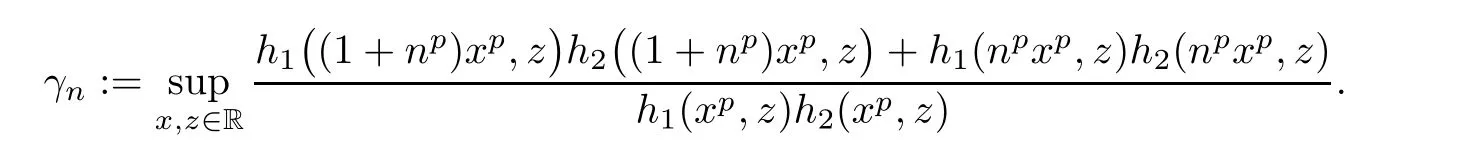
From(4.1),there is a subsequence{γnk}of a sequence{γn}such thatthat is,
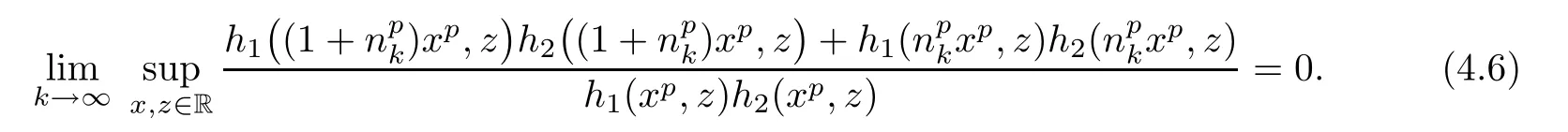
From(4.5)and(4.6),we find that

This implies that
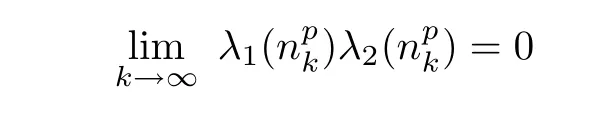
and hence
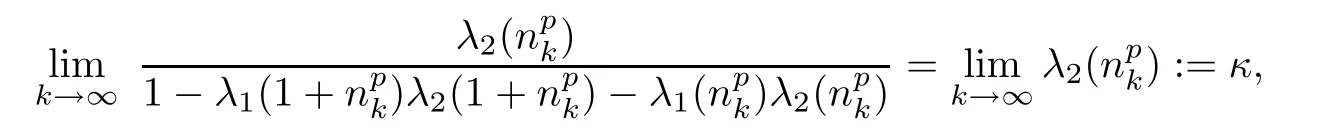
which means that λ0de fined in Theorem 3.1 is equal to κ.
By a similar method,we can prove the following corollary where κ=1.
Corollary 4.2Let h:R→(0,∞)be as in Theorem 3.2 such that
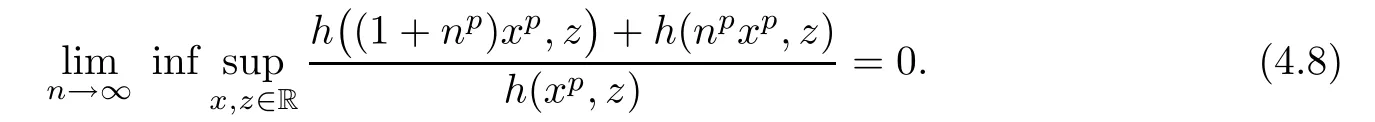
Assume that f:R→Y satis fies(1.25).Then there exist a unique p-radical function F:R→Y such that

Corollary 4.3Let θ≥ 0,r≥ 0,s,t∈R such that s+t<0.Suppose that f:R → Y such that f(0)=0 satisfy the inequality
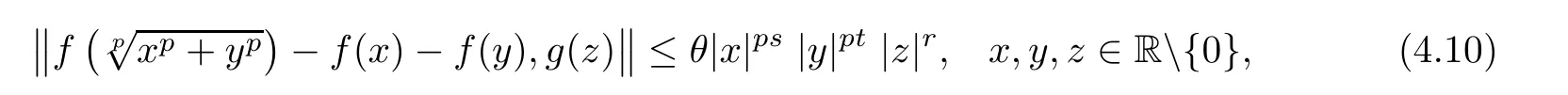
where p is odd,or f is even function satis fies(4.10)where p is even integer.Then f satis fies(1.25)on R.
ProofThe proof follows from Theorem 3.1 by de finingand h1(0,z)=h2(0,z)=0 with θ1,θ2∈ R+,r1,r2∈ R+and s,t∈ R such that θ1θ2= θ,r1+r2=r and s+t<0.
For each n∈N,we have
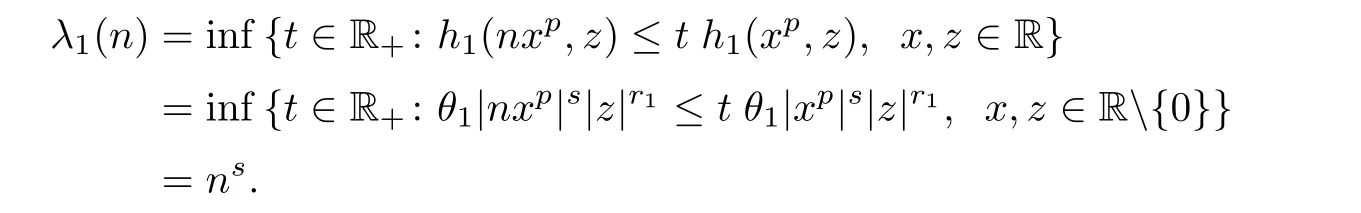
Also,we have λ2(n)=ntfor all n ∈ N.Clearly,we can find n0∈ N such that
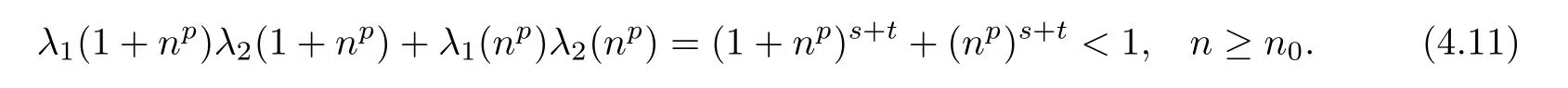
According to Theorem 3.1,there exists a unique p-radical function F:R→Y such that
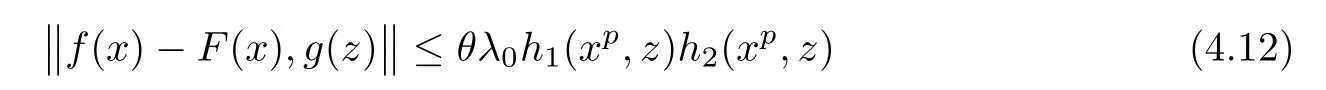
for all x,z∈R,where
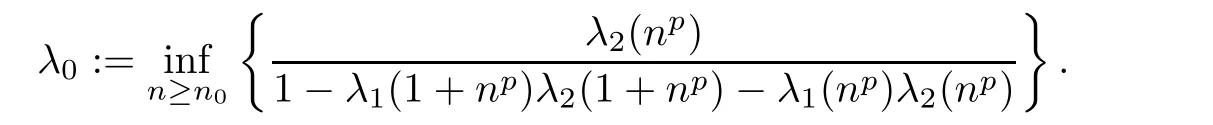
On the other hand,Since s+t<0,one of s,t must be negative.Assume that t<0.Then
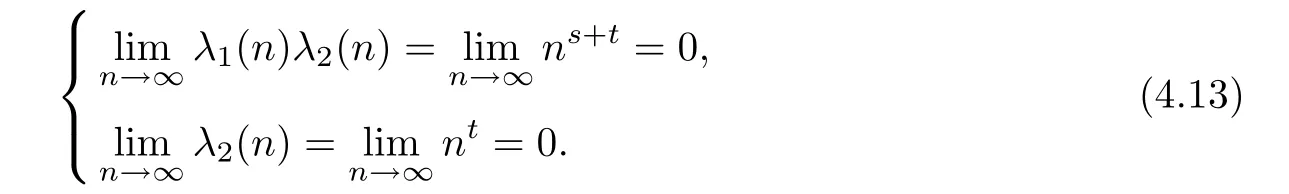
Thus by Theorem 3.3,we get the desired results.
The next corollary prove the hyperstability results for the inhomogeneous p-radical functional equation.
Corollary 4.4Let θ,s,t,r ∈ R such that θ≥ 0 and s+t<0.Assume that G:R2→ Y and f:R→Y such that f(0)=0 and satisfy the inequality
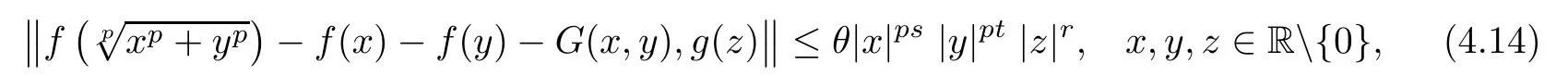
where p is odd,or f is even function satis fies(4.14)where p is even integer.If the functional equation has a solution f0:R→Y,then f is a solution to(4.15).
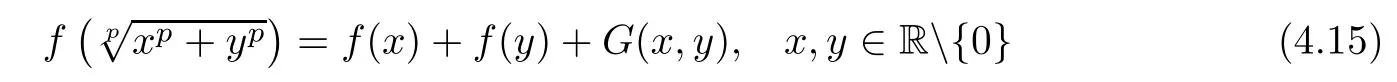
ProofFrom(4.14)we get that the function K:R→Y de fined by K:=f?f0satis fies(4.10).Consequently,Corollary 4.3 implies that K is a solution to p-radical functional equation(1.25).Therefore,
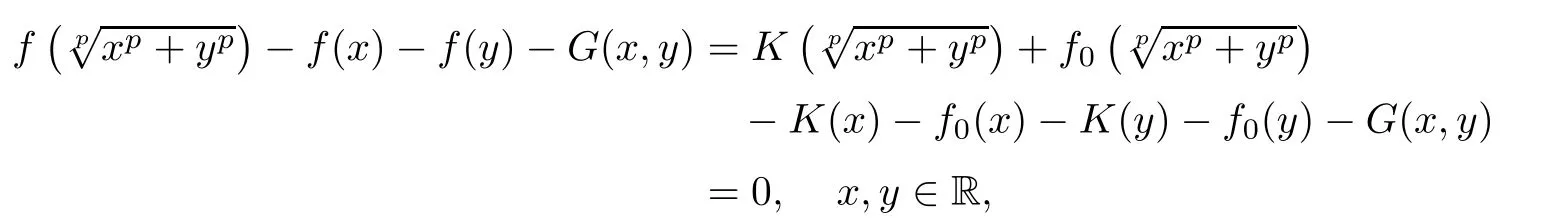
which means f is a solution to(4.15).
 Acta Mathematica Scientia(English Series)2019年2期
Acta Mathematica Scientia(English Series)2019年2期
- Acta Mathematica Scientia(English Series)的其它文章
- NUMERICAL ANALYSIS FOR VOLTERRA INTEGRAL EQUATION WITH TWO KINDS OF DELAY?
- LARGE TIME BEHAVIOR OF SOLUTION TO NONLINEAR DIRAC EQUATION IN 1+1 DIMENSIONS?
- A NONTRIVIAL SOLUTION OF A QUASILINEAR ELLIPTIC EQUATION VIA DUAL APPROACH?
- BLOW-UP PHENOMENA FOR A CLASS OF GENERALIZED DOUBLE DISPERSION EQUATIONS?
- NEW BOUNDS ON EIGENVUALUES OF LAPLACIAN?
- VECTORIAL EKELAND VARIATIONAL PRINCIPLE AND CYCLICALLY ANTIMONOTONE EQUILIBRIUM PROBLEMS?
